人教版七年级上册3.4 实际问题与一元一次方程—工程、行程问题课件(26张)
文档属性
| 名称 | 人教版七年级上册3.4 实际问题与一元一次方程—工程、行程问题课件(26张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 419.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-19 00:00:00 | ||
图片预览








文档简介
3.4 实际问题与
一元一次方程
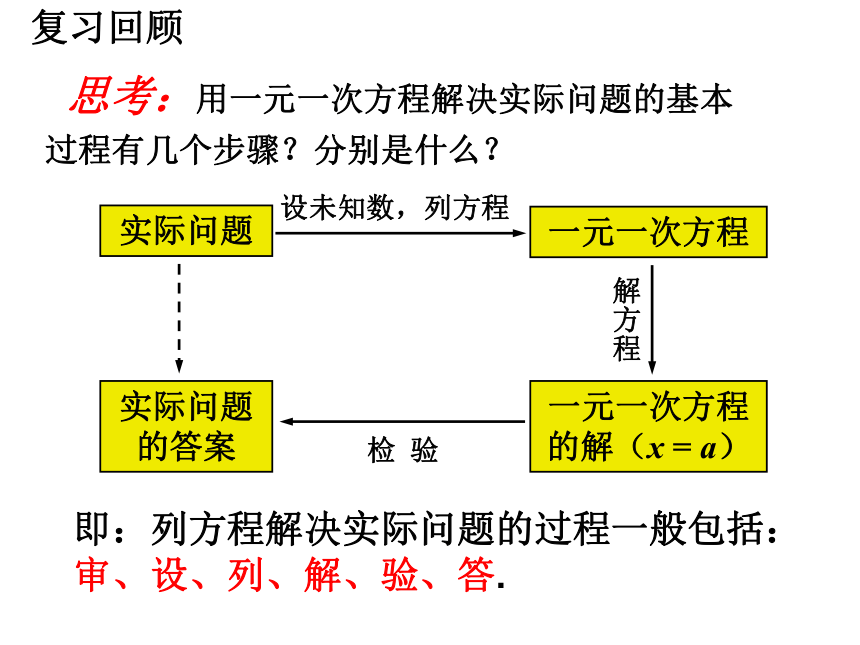
复习回顾
思考:用一元一次方程解决实际问题的基本过程有几个步骤?分别是什么?
实际问题
一元一次方程
设未知数,列方程
解方程
一元一次方程的解(x = a)
实际问题的答案
检 验
即:列方程解决实际问题的过程一般包括:审、设、列、解、验、答.
工程问题
回忆小学学习的工程问题,解决问题:
开启 智慧
(1)工程问题有哪三个基本量?这些基本量之间有怎样的关系?
(2)一件工作,如果甲单独在2小时完成,那么甲独做1小时完成全部工作的多少?
工作量=工作效率×时间;
如果一件工作需要n个小时完成,那么平均每小时完成的工作量(即工作效率)就是 .
一件工作,甲单独做x小时完成,乙单
独做y小时完成,那么甲、乙的工作效率分
别为??? ????、???? ???;甲、乙合作m小时可以完成
的工作量为??? ? 或 ???.
引例:
例1 整理一批图书,由一个人做要40 h完成.现在计划由一部分人先做4 h,再增加2人和他们一起做8 h,完成这项工作.假设这些人的工作效率相同,具体应先安排多少人工作?
列表分析:
人均效率
人数
时间
工作量
前一部分工作
x
4
后一部分工作
x+2
8
工作量之和等于总工作量1
×
=
×
×
×
=
解:设安排 x 人先做4 h.
依题意得:
解方程,得:4x+8(x+2)=40,
4x+8x+16=40,
12x=24,
x=2.
答:应先安排 2人做4 h.
P101练习2
一条地下管线由甲工程队单独铺设需要12天,由乙工程队单独铺设需要24天. 如果由这两个工程队从两端同时施工,要多少天可以铺好这条管线?
解:设要 x天可以铺好这条管线.
依题意得: ,
解方程,得: x=8.
答:两个工程队从两端同时施工,要8天可以铺好这条管线.
行程问题
行程问题中的基本关系量有哪些?它们有什么关系?
=
路程
时间
速度
×
路程
时间
速度
=
÷
速度
路程
时间
=
÷
例1 甲、乙两地相距1 500千米,两辆汽车同时从两地相向而行,其中吉普车每小时行60千米,是另一辆客车的1.5倍.
①几小时后两车相遇?
分析:若两车同时出发,则等量关系为:吉普车的路程+客车的路程=1500
解:设两车x小时后相遇,依题意可得
60x+(60÷1.5)x=1500
解得:x=15
答:15小时后两车相遇。
例1 甲、乙两地相距1 500千米,两辆汽车同时从两地相向而行,其中吉普车每小时行60千米,是另一辆客车的1.5倍.
②若吉普车先开40分钟,那么客车开出多长时间两车相遇?
①几小时后两车相遇?
甲
乙
丙
40分钟
相遇
分析:若吉普车先出发40分钟(即 小时),则等量关系为:吉普车先行的路程+吉普车后行路程+客车的路程=1500
例1 甲、乙两地相距1 500千米,两辆汽车同时从两地相向而行,其中吉普车每小时行60千米,是另一辆客车的1.5倍.
②若吉普车先开40分钟,那么客车开出多长时间两车相遇?
解:设客车开出x小时后两车相遇,依题意可得
60× +60x+(60÷1.5)x=1500
解得:x=14.6
答: 14.6小时后两车相遇。
3
2
一、相遇问题的基本题型
1、同时出发(两段)
二、相遇问题的等量关系
2、不同时出发 (三段 )
例2 甲、乙两名同学练习百米赛跑,甲每秒跑7米,乙每秒跑6.5米,如果甲让乙先跑1秒,那么甲经过几秒可以追上乙?
A起点
B
C相遇
6.5米
6.5x米
7x米
等量关系:
乙先跑的路程+乙后跑的路程=甲跑的路程
例2 甲、乙两名同学练习百米赛跑,甲每秒跑7米,乙每秒跑6.5米,如果甲让乙先跑1秒,那么甲经过几秒可以追上乙?
解:设甲经过x秒后追上乙,则依题意可得
6.5×(x+1)=7x
解得:x=13
答:甲经过13秒后追上乙。
行程问题-——追及问题
关系式:
(快行速度-慢行速度)×追及时间=相距路程
例3 甲、乙两人骑自行车,同时从相距65 km的两地相向而行,甲的速度是17.5 km/h,乙的速度为15 km/h,经过几小时,两人相距32.5 km.
相遇前相距32.5 km
等量关系:
甲走的路程+32.5+乙走的路程=65
相遇后相距32.5 km
等量关系:
甲走的路程+乙走的路程=65 +32.5
例4 一艘船从甲码头到乙码头顺流行驶,用了2小时;从乙码头返回甲码头逆流行驶,用了2.5小时,已知水流速度是3千米/时,求船在静水中的平均速度.
顺水航行速度=静水航行速度+水流速度 .
逆水航行速度=静水航行速度-水流速度.
行程问题-——航行问题
解:设船在静水中的平均速度为x千米/小时,则船顺水的速度为(x+3)千米/小时,而逆水的速度为(x-3)千米/小时.依题意可得:
2(x+3)=2.5(x-3)
解得:x=27
答:该船在静水中的速度为27千米/小时.
例5 运动场一圈为400米,张森和丁烁然一同参加学校运动会的长跑比赛。已知丁烁然平均每分钟跑230米,张森每分钟跑150米,两人从同一处听枪同向起跑,问经过多长时间两人可以首次相遇?
分析:圆形跑道中的规律:
快的人跑的路程-慢的人跑的路程=1圈(第1次相遇)
快的人跑的路程-慢的人跑的路程=2圈(第2次相遇)
快的人跑的路程-慢的人跑的路程=3圈(第3次相遇)
……….
课堂小结:
行程问题
(1)相遇问题(2)追及问题(3)航海问题
1、A、B两站间的路程为448千米,一列慢车从A站出发,每小时行驶60千米,一列快车从B站出发,每小时行驶80千米,问: (1)两车同时出发,相向而行,出发后多少小时相遇? (2)两车相向而行,慢车先开28分钟,快车开出后多长时间相遇? (3)两车同时、同向而行,如果慢车在前,出发后多长时间快车追上慢车?
2、 运动场的跑道一圈长400m,甲练习骑自行车,平均每分骑350m,乙练习跑步,平均每分跑250m.两人从同一处同时同向出发,经过多少时间首次相遇?
解:设经过x分钟首次相遇,则依题意可得
350x-250x=400 解得:x=4
答:经过4分钟甲、乙相遇。
3、某船从A码头顺流而下到B码头,然后逆流返回C码头(C码头在AB之间),共行9小时,已知船在静水中的速度为7.5千米/时,水流速度是2.5千米/时,A、C两码头相距15千米,求A、B之间的距离.
解:设A、B之间的距离为x千米,则依题意可得:
7.5+2.5
x
7.5-2.5
x-15
+ =9
解得:x=60
答:A、B之间的距离为60千米。
4. 敌军在早晨5时从距离我军7千米的驻地开始逃跑,我军发现后立即追击,速度是敌军的1.5倍,结果在7时30分追上,我军追击速度是多少?
7千米
一元一次方程
复习回顾
思考:用一元一次方程解决实际问题的基本过程有几个步骤?分别是什么?
实际问题
一元一次方程
设未知数,列方程
解方程
一元一次方程的解(x = a)
实际问题的答案
检 验
即:列方程解决实际问题的过程一般包括:审、设、列、解、验、答.
工程问题
回忆小学学习的工程问题,解决问题:
开启 智慧
(1)工程问题有哪三个基本量?这些基本量之间有怎样的关系?
(2)一件工作,如果甲单独在2小时完成,那么甲独做1小时完成全部工作的多少?
工作量=工作效率×时间;
如果一件工作需要n个小时完成,那么平均每小时完成的工作量(即工作效率)就是 .
一件工作,甲单独做x小时完成,乙单
独做y小时完成,那么甲、乙的工作效率分
别为??? ????、???? ???;甲、乙合作m小时可以完成
的工作量为??? ? 或 ???.
引例:
例1 整理一批图书,由一个人做要40 h完成.现在计划由一部分人先做4 h,再增加2人和他们一起做8 h,完成这项工作.假设这些人的工作效率相同,具体应先安排多少人工作?
列表分析:
人均效率
人数
时间
工作量
前一部分工作
x
4
后一部分工作
x+2
8
工作量之和等于总工作量1
×
=
×
×
×
=
解:设安排 x 人先做4 h.
依题意得:
解方程,得:4x+8(x+2)=40,
4x+8x+16=40,
12x=24,
x=2.
答:应先安排 2人做4 h.
P101练习2
一条地下管线由甲工程队单独铺设需要12天,由乙工程队单独铺设需要24天. 如果由这两个工程队从两端同时施工,要多少天可以铺好这条管线?
解:设要 x天可以铺好这条管线.
依题意得: ,
解方程,得: x=8.
答:两个工程队从两端同时施工,要8天可以铺好这条管线.
行程问题
行程问题中的基本关系量有哪些?它们有什么关系?
=
路程
时间
速度
×
路程
时间
速度
=
÷
速度
路程
时间
=
÷
例1 甲、乙两地相距1 500千米,两辆汽车同时从两地相向而行,其中吉普车每小时行60千米,是另一辆客车的1.5倍.
①几小时后两车相遇?
分析:若两车同时出发,则等量关系为:吉普车的路程+客车的路程=1500
解:设两车x小时后相遇,依题意可得
60x+(60÷1.5)x=1500
解得:x=15
答:15小时后两车相遇。
例1 甲、乙两地相距1 500千米,两辆汽车同时从两地相向而行,其中吉普车每小时行60千米,是另一辆客车的1.5倍.
②若吉普车先开40分钟,那么客车开出多长时间两车相遇?
①几小时后两车相遇?
甲
乙
丙
40分钟
相遇
分析:若吉普车先出发40分钟(即 小时),则等量关系为:吉普车先行的路程+吉普车后行路程+客车的路程=1500
例1 甲、乙两地相距1 500千米,两辆汽车同时从两地相向而行,其中吉普车每小时行60千米,是另一辆客车的1.5倍.
②若吉普车先开40分钟,那么客车开出多长时间两车相遇?
解:设客车开出x小时后两车相遇,依题意可得
60× +60x+(60÷1.5)x=1500
解得:x=14.6
答: 14.6小时后两车相遇。
3
2
一、相遇问题的基本题型
1、同时出发(两段)
二、相遇问题的等量关系
2、不同时出发 (三段 )
例2 甲、乙两名同学练习百米赛跑,甲每秒跑7米,乙每秒跑6.5米,如果甲让乙先跑1秒,那么甲经过几秒可以追上乙?
A起点
B
C相遇
6.5米
6.5x米
7x米
等量关系:
乙先跑的路程+乙后跑的路程=甲跑的路程
例2 甲、乙两名同学练习百米赛跑,甲每秒跑7米,乙每秒跑6.5米,如果甲让乙先跑1秒,那么甲经过几秒可以追上乙?
解:设甲经过x秒后追上乙,则依题意可得
6.5×(x+1)=7x
解得:x=13
答:甲经过13秒后追上乙。
行程问题-——追及问题
关系式:
(快行速度-慢行速度)×追及时间=相距路程
例3 甲、乙两人骑自行车,同时从相距65 km的两地相向而行,甲的速度是17.5 km/h,乙的速度为15 km/h,经过几小时,两人相距32.5 km.
相遇前相距32.5 km
等量关系:
甲走的路程+32.5+乙走的路程=65
相遇后相距32.5 km
等量关系:
甲走的路程+乙走的路程=65 +32.5
例4 一艘船从甲码头到乙码头顺流行驶,用了2小时;从乙码头返回甲码头逆流行驶,用了2.5小时,已知水流速度是3千米/时,求船在静水中的平均速度.
顺水航行速度=静水航行速度+水流速度 .
逆水航行速度=静水航行速度-水流速度.
行程问题-——航行问题
解:设船在静水中的平均速度为x千米/小时,则船顺水的速度为(x+3)千米/小时,而逆水的速度为(x-3)千米/小时.依题意可得:
2(x+3)=2.5(x-3)
解得:x=27
答:该船在静水中的速度为27千米/小时.
例5 运动场一圈为400米,张森和丁烁然一同参加学校运动会的长跑比赛。已知丁烁然平均每分钟跑230米,张森每分钟跑150米,两人从同一处听枪同向起跑,问经过多长时间两人可以首次相遇?
分析:圆形跑道中的规律:
快的人跑的路程-慢的人跑的路程=1圈(第1次相遇)
快的人跑的路程-慢的人跑的路程=2圈(第2次相遇)
快的人跑的路程-慢的人跑的路程=3圈(第3次相遇)
……….
课堂小结:
行程问题
(1)相遇问题(2)追及问题(3)航海问题
1、A、B两站间的路程为448千米,一列慢车从A站出发,每小时行驶60千米,一列快车从B站出发,每小时行驶80千米,问: (1)两车同时出发,相向而行,出发后多少小时相遇? (2)两车相向而行,慢车先开28分钟,快车开出后多长时间相遇? (3)两车同时、同向而行,如果慢车在前,出发后多长时间快车追上慢车?
2、 运动场的跑道一圈长400m,甲练习骑自行车,平均每分骑350m,乙练习跑步,平均每分跑250m.两人从同一处同时同向出发,经过多少时间首次相遇?
解:设经过x分钟首次相遇,则依题意可得
350x-250x=400 解得:x=4
答:经过4分钟甲、乙相遇。
3、某船从A码头顺流而下到B码头,然后逆流返回C码头(C码头在AB之间),共行9小时,已知船在静水中的速度为7.5千米/时,水流速度是2.5千米/时,A、C两码头相距15千米,求A、B之间的距离.
解:设A、B之间的距离为x千米,则依题意可得:
7.5+2.5
x
7.5-2.5
x-15
+ =9
解得:x=60
答:A、B之间的距离为60千米。
4. 敌军在早晨5时从距离我军7千米的驻地开始逃跑,我军发现后立即追击,速度是敌军的1.5倍,结果在7时30分追上,我军追击速度是多少?
7千米
