人教版七年级数学下册5.2.2 平行线的判定 课件(共20张ppt)
文档属性
| 名称 | 人教版七年级数学下册5.2.2 平行线的判定 课件(共20张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-19 00:00:00 | ||
图片预览





文档简介
5.2 平行线
第Ⅱ课时 平行线的判定
学习目标
1.掌握平行线的三种判定方法,会运用判定方法来判断两条
直线是否平行.
2.能够根据平行线的判定方法进行简单的推理.
问:判断两直线平行有那些方法?
1.如果两条直线与第三条直线平行,那么这两条直线也互相平行。
2.同位角相等,两直线平行。
3.内错角相等,两直线平行。
4.同旁内角互补,两直线平行。
这些定理都可以直接
判定两条直线平行
课前预习:温故知新
经 典 数 学
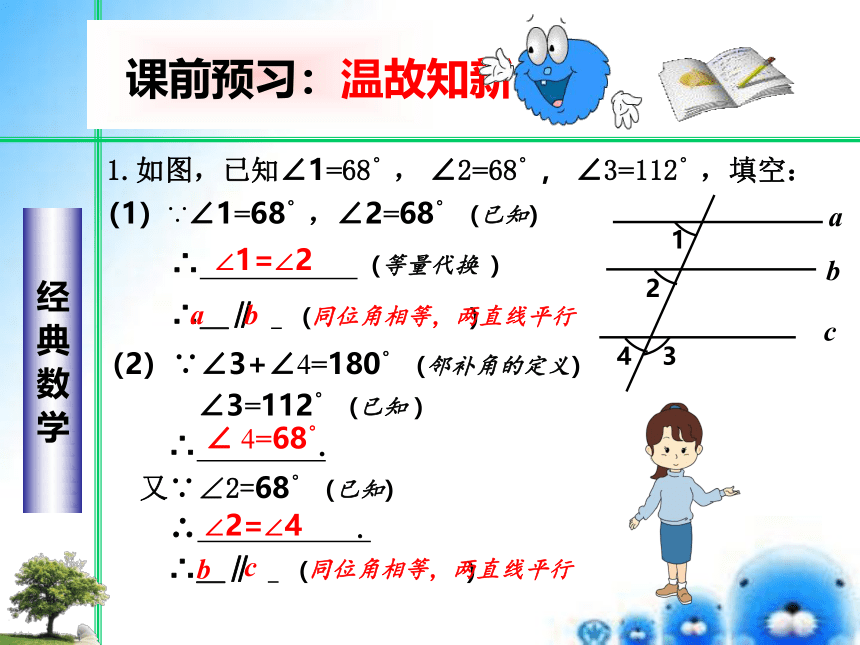
1.如图,已知∠1=68。, ∠2=68。, ∠3=112。,填空:
a
b
1
2
3
4
(1)∵∠1=68。,∠2=68。(已知)
∴ (等量代换 )
∴_∥ _( )
a
b
∠1=∠2
同位角相等,两直线平行
(2)∵∠3+∠4=180。(邻补角的定义)
∠3=112。(已知 )
∴ .
又∵∠2=68。(已知)
∴ .
∴_∥ _( )
∠ 4=68。
∠2=∠4
b
c
同位角相等,两直线平行
c
学以致用
2
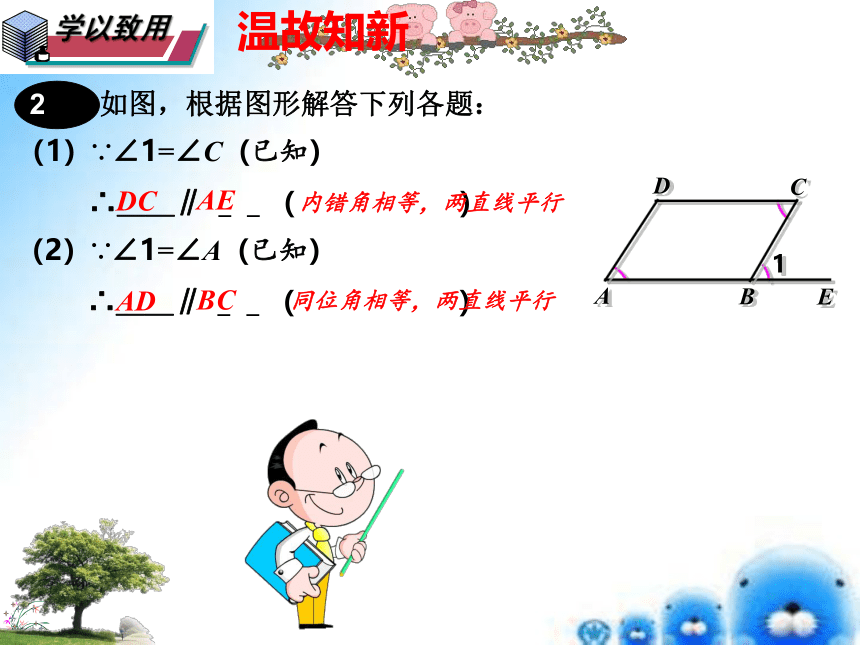
如图,根据图形解答下列各题:
(1)∵∠1=∠C(已知)
∴__∥ __( )
DC
AE
内错角相等,两直线平行
(2)∵∠1=∠A(已知)
∴__∥ __( )
AD
BC
同位角相等,两直线平行
1
A
B
E
C
D
温故知新
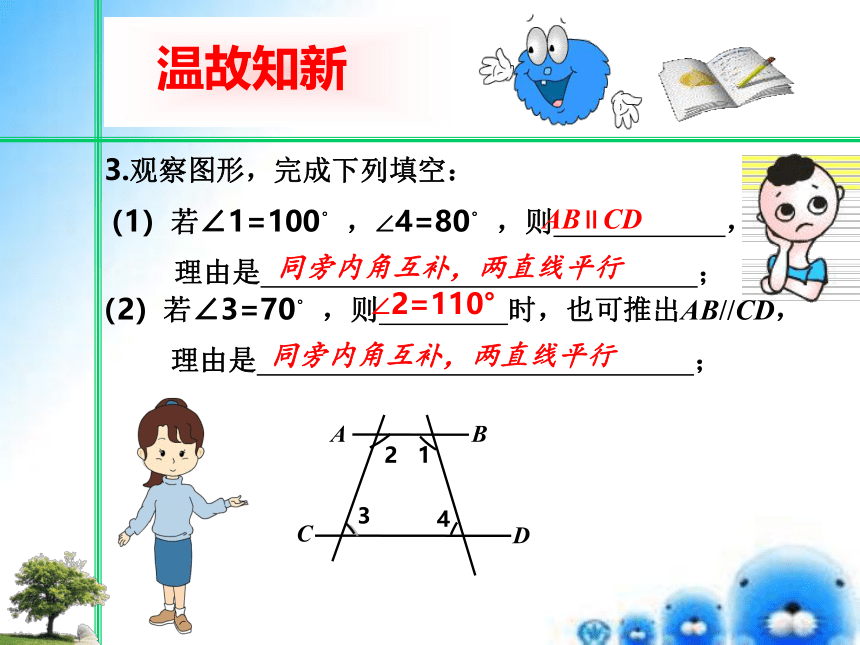
3.观察图形,完成下列填空:
(1)若∠1=100。 ,∠4=80。 ,则 ,
理由是 ;
(2)若∠3=70。 ,则 时,也可推出AB//CD,
理由是 ;
A
B
C
D
1
2
3
4
AB∥CD
同旁内角互补,两直线平行
∠2=110°
同旁内角互补,两直线平行
温故知新
温故知新
平行线判定示意图
同位角相等
内错角相等
同旁内角互补
两直线平行
判定
数量关系
位置关系
温馨提示:平行线的判定是先有角的关系,然后得到两直线平行!
说一说
例 2
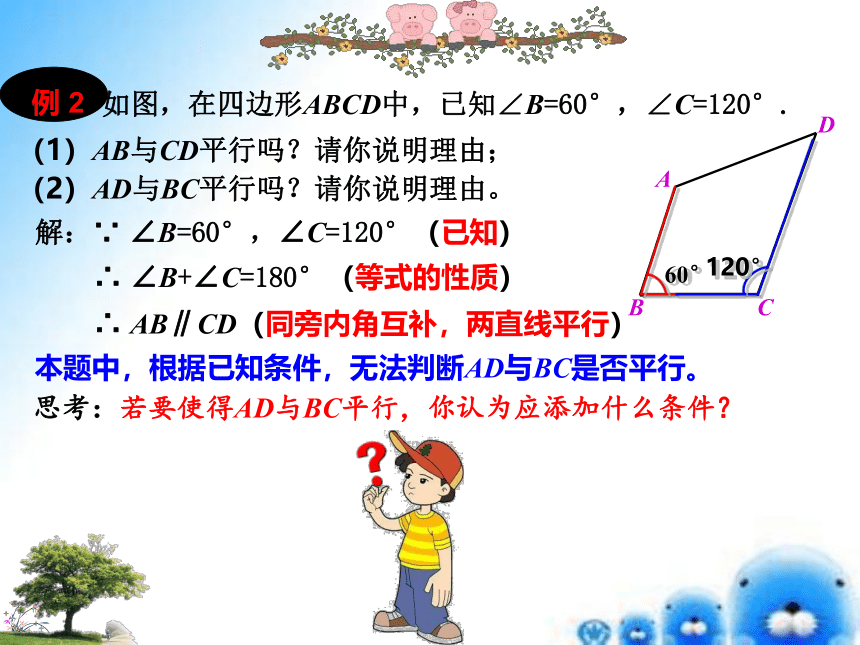
如图,在四边形ABCD中,已知∠B=60°,∠C=120°.
(1)AB与CD平行吗?请你说明理由;
(2)AD与BC平行吗?请你说明理由。
解:∵ ∠B=60°,∠C=120°(已知)
∴ ∠B+∠C=180°(等式的性质)
∴ AB∥CD(同旁内角互补,两直线平行)
A
B
C
D
60°
120°
本题中,根据已知条件,无法判断AD与BC是否平行。
思考:若要使得AD与BC平行,你认为应添加什么条件?
大家谈谈
如图,在同一平面内,直线CD,EF均与直线AB垂直,D、F为垂足。试判断CD与EF是否平行?
1
2
C
E
B
D
F
A
解:∵CD⊥AB,EF⊥AB(已知)
∴∠1=∠2=90°(垂线的定义)
∴ CD∥EF(同位角相等,两直线平行)
基本事实
在同一平面内,垂直于同一条直线的两条直线平行。
判断两条直线平行有哪些方法?
例3
式子表示:
∵ CD⊥AB,EF⊥AB(
∴CD∥EF
归纳总结:
判定方法1:如果两条直线与第三条直线平行,那么这两条直线也互相平行。
判定方法2:同位角相等,两直线平行。
判定方法3:内错角相等,两直线平行。
判定方法4:同旁内角互补,两直线平行。
判定方法5:在同一平面内,垂直于同一条直线的两条直线平行
这些定理都可以直接
判定两条直线平行
例 4
如图,直线a、b被直线c所截。
(1)已知∠1=150°,∠2=150°,a//b吗? 试说明理由。
1
2
b
c
a
3
4
∵∠1=150°,∠2=150°( )
解:
∴∠1=∠2( )
∴a∥b( )
已知
等量代换
内错角相等,两直线平行
(2)若将“∠2=150°”替换为“∠3=150°”,那么a//b吗?
(3)若将“∠2=150°”替换为“∠4=30°”,那么a//b吗?
数 学 活 动 室
6.在下列解答中,填上适当的理由。
(1)∵ ∠B =∠1(已知 )
∴ AD∥BC( )
(2)∵ ∠D =∠1(已知)
∴ AB∥CD( )
同位角相等,两直线平行
内错角相等,两直线平行
A
B
C
D
1
7.在下列解答中,填空:
(1)∵ ∠BAD +∠ABC =180°
∴ ___∥___(同旁内角互补,两直线平行)
(2)∵ ∠BCD +∠ABC =180°
∴ ___∥___ (同旁内角互补,两直线平行)
D
A
B
C
AB
DC
BC
AD
数 学 活 动 室
8.反馈评价游戏接龙
(1)如果∠A=∠3,那么 ∥ ,
( )
(2)如果∠2=∠E,那么 ∥ ,
( )
(3)如果∠A+∠ABE=1800,那么 ∥ ,
( )
(4)如果∠2= ,那么DA∥EB
( )
(5)如果∠DBC+ =1800,那么DB∥EC
( )
AD BE
同位角相等,两直线平行.
BD CE
内错角相等,两直线平行.
AD BE
同旁内角互补,两直线平行.
∠D
A
B
C
D
E
1
2
3
内错角相等,两直线平行.
∠C
同旁内角互补,两直线平行.
数 学 活 动 室
9.如图,哪两个角相等能判定直线AB∥CD?
1
4
3
2
A
D
C
B
10.已知∠1=54°,当 时,AB∥CD?
A
B
C
D
E
1
2
3
我的收获是……
这节课我学到了什么?
我还有……的疑惑
畅谈收获
小 结
习题 5.2
P 179
第3、4题
扩展训练:
1
如图,∠1=65°,∠2=65°, ∠3=115°.
试说明:DE//BC,DF//AB.根据图形,完成下面的推理。
解:∵ ∠1=65°,∠2=65°( )
∴ ∠1=∠2 ( )
∴ ∥ ( )
我能行!
F
D
A
E
B
C
3
4
1
2
∵ AB与DE相交
∴ ∠1=∠4 ( )
∴ ∠4=65°( )
∵ ∠3=115°
∴ ∠3+∠ 4=180°( )
∴ ∥ ( )
DE
BC
已知
等量代换
同位角相等,两直线平行
对顶角相等
等量代换
等式的性质
同旁内角互补,两直线平行
AB
DF
2.如图,BC、DE分别平分?ABD和?BDF,且?1=?2,
请找出平行线,并说明理由。
A
B
D
F
C
E
2
1
3
4
一个人一天也不能没有理想,凭侥幸、怕吃苦、没有真才实学,再好的理想也不能实现不了。
谢谢大家光临指导
第Ⅱ课时 平行线的判定
学习目标
1.掌握平行线的三种判定方法,会运用判定方法来判断两条
直线是否平行.
2.能够根据平行线的判定方法进行简单的推理.
问:判断两直线平行有那些方法?
1.如果两条直线与第三条直线平行,那么这两条直线也互相平行。
2.同位角相等,两直线平行。
3.内错角相等,两直线平行。
4.同旁内角互补,两直线平行。
这些定理都可以直接
判定两条直线平行
课前预习:温故知新
经 典 数 学
1.如图,已知∠1=68。, ∠2=68。, ∠3=112。,填空:
a
b
1
2
3
4
(1)∵∠1=68。,∠2=68。(已知)
∴ (等量代换 )
∴_∥ _( )
a
b
∠1=∠2
同位角相等,两直线平行
(2)∵∠3+∠4=180。(邻补角的定义)
∠3=112。(已知 )
∴ .
又∵∠2=68。(已知)
∴ .
∴_∥ _( )
∠ 4=68。
∠2=∠4
b
c
同位角相等,两直线平行
c
学以致用
2
如图,根据图形解答下列各题:
(1)∵∠1=∠C(已知)
∴__∥ __( )
DC
AE
内错角相等,两直线平行
(2)∵∠1=∠A(已知)
∴__∥ __( )
AD
BC
同位角相等,两直线平行
1
A
B
E
C
D
温故知新
3.观察图形,完成下列填空:
(1)若∠1=100。 ,∠4=80。 ,则 ,
理由是 ;
(2)若∠3=70。 ,则 时,也可推出AB//CD,
理由是 ;
A
B
C
D
1
2
3
4
AB∥CD
同旁内角互补,两直线平行
∠2=110°
同旁内角互补,两直线平行
温故知新
温故知新
平行线判定示意图
同位角相等
内错角相等
同旁内角互补
两直线平行
判定
数量关系
位置关系
温馨提示:平行线的判定是先有角的关系,然后得到两直线平行!
说一说
例 2
如图,在四边形ABCD中,已知∠B=60°,∠C=120°.
(1)AB与CD平行吗?请你说明理由;
(2)AD与BC平行吗?请你说明理由。
解:∵ ∠B=60°,∠C=120°(已知)
∴ ∠B+∠C=180°(等式的性质)
∴ AB∥CD(同旁内角互补,两直线平行)
A
B
C
D
60°
120°
本题中,根据已知条件,无法判断AD与BC是否平行。
思考:若要使得AD与BC平行,你认为应添加什么条件?
大家谈谈
如图,在同一平面内,直线CD,EF均与直线AB垂直,D、F为垂足。试判断CD与EF是否平行?
1
2
C
E
B
D
F
A
解:∵CD⊥AB,EF⊥AB(已知)
∴∠1=∠2=90°(垂线的定义)
∴ CD∥EF(同位角相等,两直线平行)
基本事实
在同一平面内,垂直于同一条直线的两条直线平行。
判断两条直线平行有哪些方法?
例3
式子表示:
∵ CD⊥AB,EF⊥AB(
∴CD∥EF
归纳总结:
判定方法1:如果两条直线与第三条直线平行,那么这两条直线也互相平行。
判定方法2:同位角相等,两直线平行。
判定方法3:内错角相等,两直线平行。
判定方法4:同旁内角互补,两直线平行。
判定方法5:在同一平面内,垂直于同一条直线的两条直线平行
这些定理都可以直接
判定两条直线平行
例 4
如图,直线a、b被直线c所截。
(1)已知∠1=150°,∠2=150°,a//b吗? 试说明理由。
1
2
b
c
a
3
4
∵∠1=150°,∠2=150°( )
解:
∴∠1=∠2( )
∴a∥b( )
已知
等量代换
内错角相等,两直线平行
(2)若将“∠2=150°”替换为“∠3=150°”,那么a//b吗?
(3)若将“∠2=150°”替换为“∠4=30°”,那么a//b吗?
数 学 活 动 室
6.在下列解答中,填上适当的理由。
(1)∵ ∠B =∠1(已知 )
∴ AD∥BC( )
(2)∵ ∠D =∠1(已知)
∴ AB∥CD( )
同位角相等,两直线平行
内错角相等,两直线平行
A
B
C
D
1
7.在下列解答中,填空:
(1)∵ ∠BAD +∠ABC =180°
∴ ___∥___(同旁内角互补,两直线平行)
(2)∵ ∠BCD +∠ABC =180°
∴ ___∥___ (同旁内角互补,两直线平行)
D
A
B
C
AB
DC
BC
AD
数 学 活 动 室
8.反馈评价游戏接龙
(1)如果∠A=∠3,那么 ∥ ,
( )
(2)如果∠2=∠E,那么 ∥ ,
( )
(3)如果∠A+∠ABE=1800,那么 ∥ ,
( )
(4)如果∠2= ,那么DA∥EB
( )
(5)如果∠DBC+ =1800,那么DB∥EC
( )
AD BE
同位角相等,两直线平行.
BD CE
内错角相等,两直线平行.
AD BE
同旁内角互补,两直线平行.
∠D
A
B
C
D
E
1
2
3
内错角相等,两直线平行.
∠C
同旁内角互补,两直线平行.
数 学 活 动 室
9.如图,哪两个角相等能判定直线AB∥CD?
1
4
3
2
A
D
C
B
10.已知∠1=54°,当 时,AB∥CD?
A
B
C
D
E
1
2
3
我的收获是……
这节课我学到了什么?
我还有……的疑惑
畅谈收获
小 结
习题 5.2
P 179
第3、4题
扩展训练:
1
如图,∠1=65°,∠2=65°, ∠3=115°.
试说明:DE//BC,DF//AB.根据图形,完成下面的推理。
解:∵ ∠1=65°,∠2=65°( )
∴ ∠1=∠2 ( )
∴ ∥ ( )
我能行!
F
D
A
E
B
C
3
4
1
2
∵ AB与DE相交
∴ ∠1=∠4 ( )
∴ ∠4=65°( )
∵ ∠3=115°
∴ ∠3+∠ 4=180°( )
∴ ∥ ( )
DE
BC
已知
等量代换
同位角相等,两直线平行
对顶角相等
等量代换
等式的性质
同旁内角互补,两直线平行
AB
DF
2.如图,BC、DE分别平分?ABD和?BDF,且?1=?2,
请找出平行线,并说明理由。
A
B
D
F
C
E
2
1
3
4
一个人一天也不能没有理想,凭侥幸、怕吃苦、没有真才实学,再好的理想也不能实现不了。
谢谢大家光临指导
