人教版七年级数学下册课件 第五章 相交线与平行线 5.1.3 同位角、内错角、同旁内角(共30张ppt)
文档属性
| 名称 | 人教版七年级数学下册课件 第五章 相交线与平行线 5.1.3 同位角、内错角、同旁内角(共30张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-19 00:00:00 | ||
图片预览











文档简介
第五章 相交线与平行线
5.1.3 同位角、内错角、同旁内角
2021
【学习目标】
1.知道同位角、内错角、同旁内角的概念;
2.会结合图形识别同位角、内错角、同旁内角.
【课前预习】
1.角α和β是同旁内角,若∠α=48°,则∠β的度数为( )
A.48° B.132° C.48°或132° D.无法确定
2.下列说法中错误的是( )
A.同旁内角互补,两直线平行 B.两直线平行,内错角相等
C.同位角相等 D.对顶角相等
3.己知∠1与∠2是两条直线被第三条直线所截形成的同位角,若∠1=60,°则∠2为( )
A.60° B.120° C.60°或120° D.不能确定
4.两条平行直线被第三条直线所截时,产生的八个角中,角平分线互相平行的两个角是( ).
A.同位角 B.同旁内角 C.内错角 D.同位角或内错角
5.下列推理正确的是( )
A.∵∠1+∠2=90°,∠2+∠3=90°,∴∠1+∠3=90°
B.∵∠1+∠3=90°,∠3+∠2=90°,∴∠1=∠2
C.∵∠1与∠2是对顶角,又∠2=∠3,∴∠1与∠3是对顶角
D.∵∠1与∠2是同位角,又∠2与∠3是同位角,∴∠1与∠3是同位角
【课前预习】答案
1.D
2.C
3.D
4.D
5.B
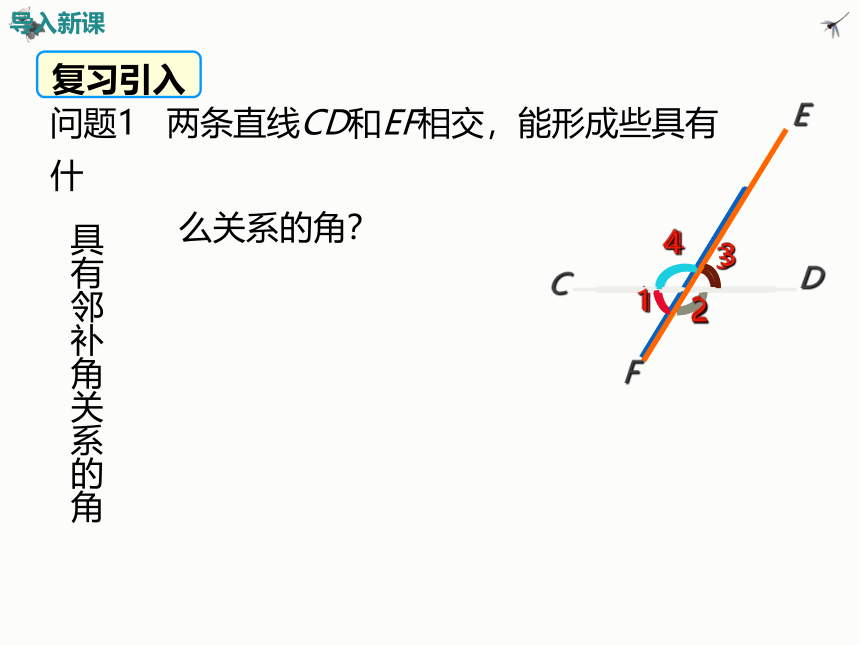
问题1 两条直线CD和EF相交,能形成些具有什
么关系的角?
3
2
2
1
3
4
1
4
C
D
E
F
1
3
4
2
具有邻补角关系的角
导入新课
复习引入
A
B
E
F
1
3
4
2
4
2
3
1
问题2 两条直线AB和EF相交,能形成些具有什么关
系的角?
具有对顶角关系的角
6
7
5
8
简称“三线八角”
若再添加一条直线,即直线EF被第三条直线CD所截,构成了几个角?有什么特点?
B
A
F
E
C
D
4
3
1
2
讲授新课
同位角、内错角、同旁内角
a
b
c
通常说:两条直线被第三条直线所截
截线
如:直线a、b被直线c 所截.
被截线
F
活动1 观察∠1与∠5的位置关系:
①在直线EF的同旁(右边)
②在直线AB、CD的同一侧(上方)
A
C
B
D
E
1
2
3
4
5
6
7
8
1
5
∠2和∠6;∠3和∠7;∠4和∠8
图中的同位角还有哪些?
同位角
一、同位角的概念
A
A.(1),(2) B.(3),(4)
C.(1),(2),(3) D.(2),(3) ,(3)
例1:下列图形中,∠1和∠2是同位角的有( )
1
2
1
2
1
2
1
2
(1) (2) (3) (4)
图形特征:在形如字母“F”的图形中有同位角.
变式图形:图中的∠1与∠2都是同位角.
1
2
1
2
1
2
1
2
A
C
B
D
E
F
1
2
3
4
5
6
7
8
活动2 观察∠3与∠5的位置关系:
①在直线EF的两侧
②在直线AB、CD之间
3
5
∠4和∠6
图中的内错角还有哪些?
内错角
二、内错角的概念
例2:如图,与∠1是内错角的是( )
1
3
2
4
5
A. ∠2 B. ∠3
C. ∠4 D. ∠5
B
变式图形:图中的∠1与∠2都是内错角.
图形特征:在形如“Z”的图形中有内错角.
1
2
1
1
1
2
2
2
A
C
B
D
E
F
1
2
3
4
5
6
7
8
活动3 观察∠4与∠5的位置关系
①在直线EF的同旁
②在直线AB、CD之间
4
5
∠3和∠6
图中还有哪些同旁内角?
同旁内角
三、同旁内角的概念
例3:下列图形中,∠1和∠2是同旁内角的有( )
1
1
A
B
C
D
1
2
2
2
1
2
A
变式图形:图中的∠1与∠2都是同旁内角.
图形特征:在形如“U”的图形中有同旁内角.
1
1
1
1
2
2
2
2
同位角、内错角和同旁内角的结构特征:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}角的
名称
角的特征
基本图形
基本图形
相同点
共同特征
同位角
同旁
内角
内错角
F
Z
U
截线:同侧
被截线:同旁
截线:同侧
被截线:之间
截线:两侧
被截线:之间
1
2
1
2
1
2
都在截线同侧
都在被截线之间
这三类角都是没有公共顶点的.
总结归纳
例4 如图,直线DE截AB ,AC,构成8个角,指出所有的同位角,内错角,同旁内角.
解:两条直线是AB,AC,截线是DE,所以8个角中,同位角:∠2与∠5,∠4与∠7,∠1与∠8, ∠6和∠3;内错角:∠4与∠5,∠1与∠6;同旁内角:∠1与∠5,∠4与∠6.
E
D
C
B
A
8
7
6
5
4
3
2
1
变式:∠A与∠8是哪两条直线被哪条直线所截的角?它们是什么关系的角?∠A与∠5呢?∠A与∠6呢?
E
D
C
B
A
8
7
6
5
4
3
2
1
解:∠A与∠8是直线AB,DE被直线AC所截形成的内错角.
∠A与∠5是直线AB,DE被直线AC所截形成的同旁内角.
∠A与∠6是直线AB,DE被直线AC所截形成的同位角.
练一练:识别这些角是同位角、内错角还是同旁内角
1
2
(1)
同位角
1
2
(2)
1
2
(3)
1
2
(4)
1
2
(5)
1
2
(6)
1
2
(7)
1
2
(8)
1
2
1
2
(9)
(10)
同位角
同位角
同位角
同位角
内错角
同旁内角
例5 如图,直线DE,BC被直线AB所截.
(1)∠1与∠2, ∠1和∠3,∠1和∠4各是什么角?
4
3
2
1
F
E
D
C
B
A
解:(1)∠1与∠2是内错角,∠1和∠3同旁内角,∠1和∠4是同位角.
温馨提示:解题之前要明确哪两条直线被哪条直线所截.
解:(2)如果∠1=∠4,由对顶角相等,得∠2=∠4,那么∠1=∠2.因为∠3和∠4互补,即∠4+∠3=180°,又因为∠1=∠4,所以∠1+∠3=180°,即∠1与∠3互补.
4
3
2
1
F
E
D
C
B
A
(2)如果∠1=∠4,那么∠1与∠2相等吗?∠1与
∠3互补吗? 为什么?
生活中的数学:三线八角手势记忆法
同位角
内错角
同旁内角
小 结
2、掌握辩别这些角的关键是看哪两条直线被哪一条直线所截、分清哪一条直线截哪两条直线形成了哪些角,是作出正确判定的前提,在截线的同旁找同位角,同旁内角,在截线的不同旁,找内错角.
1、同位角、内错角、同旁内角都是两条直线被第三条直线所截时产生的,我们要掌握他们的位置特征.
【课后练习】
1.在我们常见的英文字母中,也存在着同位角、内错角、同旁内角.在下面几个字母中,含有内错角最少的字母是( )
A.H B.M C.N D.A
2.平面上三条直线两两相交最多能构成对顶角的对数是( ).
A.7 B.6 C.5 D.4
3.下列说法中,正确的是( )
A.相等的两个角是对顶角
B.有一条公共边的两个角是邻补角
C.有公共顶点的两个角是对顶角
D.一条直线与端点在这条直线上的一条射线组成的两个角是邻补角
4.若∠A与∠B是对顶角且互补,则它们两边所在的直线( )
A.互相垂直 B.互相平行
C.既不垂直也不平行 D.不能确定
5.已知∠1与∠2是同旁内角,若∠1=50°,则∠2的度数是( )
A.130° B.50° C.100° D.不能确定
6.如图,两只手的食指和拇指在同一个平面内,它们构成的一对角可看成是( )
A.同位角 B.内错角 C.对顶角 D.同旁内角
7.若∠1与∠2是同位角,则它们之间的关系是( ).
A.∠1=∠2 ; B.∠1>∠2 ;
C.∠1<∠2; D.∠1=∠2或∠1>∠2或∠1<∠2.
8.在我们常见的英文字母中,存在着同位角、内错角、同旁内角的现象.在下列几个字母中,不含同旁内角现象的字母是( )
A.E B.F C.N D.H
9.下列命题中正确的有( )个.
①=a;②同位角相等;③过一点有且只有一条直线垂直于已知直线;④一个数的平方根等于它本身,这个数是0和1;⑤经过直线外一点有且只有一条直线与这条直线平行.
A.1 B.2 C.3 D.4
10.若∠A与∠B是对顶角且互补,则它们两边所在的直线( )
A.互相垂直 B.互相平行 C.既不垂直也不平行 D.不能确定
11..四条直线两两相交,且任意三条直线不相交于同点,则四条直线共可构成的同位角有________对.
12.若∠1与∠2是对顶角,且∠1与∠2互余,则∠1=________,∠2=________.
13.两条直线相交所成的四个角中,有两个角分别是(2x-10)°和(110-x)°,则x=_____.
14.探究题:
(1)三条直线相交,最少有__________个交点,最多有__________个交点,分别画出图形,并数出图形中的对顶角和邻补角的对数;
(2)四条直线相交,最少有__________个交点,最多有__________个交点,分别画出图形,并数出图形中的对顶角和邻补角的对数;
(3)依次类推,n条直线相交,最少有__________个交点,最多有__________个交点,对顶角有_________对,邻补角有__________对.
15.如图,在直线DE与∠O的两边相交,则∠O的同位角是_______,∠8的内错角是_______,∠1的同旁内角是_______.
【课后练习】答案
1.C 2.B 3.D 4.A 5.D 6.B 7.D 8.C 9.A 10.A
11.48
12. 45°, 45°
13.40或80
14.(1)1,3;(2)1,6;(3)1, ,n(n-1),2n(n-1)
15.∠2和∠5;∠2;∠8和∠O
5.1.3 同位角、内错角、同旁内角
2021
【学习目标】
1.知道同位角、内错角、同旁内角的概念;
2.会结合图形识别同位角、内错角、同旁内角.
【课前预习】
1.角α和β是同旁内角,若∠α=48°,则∠β的度数为( )
A.48° B.132° C.48°或132° D.无法确定
2.下列说法中错误的是( )
A.同旁内角互补,两直线平行 B.两直线平行,内错角相等
C.同位角相等 D.对顶角相等
3.己知∠1与∠2是两条直线被第三条直线所截形成的同位角,若∠1=60,°则∠2为( )
A.60° B.120° C.60°或120° D.不能确定
4.两条平行直线被第三条直线所截时,产生的八个角中,角平分线互相平行的两个角是( ).
A.同位角 B.同旁内角 C.内错角 D.同位角或内错角
5.下列推理正确的是( )
A.∵∠1+∠2=90°,∠2+∠3=90°,∴∠1+∠3=90°
B.∵∠1+∠3=90°,∠3+∠2=90°,∴∠1=∠2
C.∵∠1与∠2是对顶角,又∠2=∠3,∴∠1与∠3是对顶角
D.∵∠1与∠2是同位角,又∠2与∠3是同位角,∴∠1与∠3是同位角
【课前预习】答案
1.D
2.C
3.D
4.D
5.B
问题1 两条直线CD和EF相交,能形成些具有什
么关系的角?
3
2
2
1
3
4
1
4
C
D
E
F
1
3
4
2
具有邻补角关系的角
导入新课
复习引入
A
B
E
F
1
3
4
2
4
2
3
1
问题2 两条直线AB和EF相交,能形成些具有什么关
系的角?
具有对顶角关系的角
6
7
5
8
简称“三线八角”
若再添加一条直线,即直线EF被第三条直线CD所截,构成了几个角?有什么特点?
B
A
F
E
C
D
4
3
1
2
讲授新课
同位角、内错角、同旁内角
a
b
c
通常说:两条直线被第三条直线所截
截线
如:直线a、b被直线c 所截.
被截线
F
活动1 观察∠1与∠5的位置关系:
①在直线EF的同旁(右边)
②在直线AB、CD的同一侧(上方)
A
C
B
D
E
1
2
3
4
5
6
7
8
1
5
∠2和∠6;∠3和∠7;∠4和∠8
图中的同位角还有哪些?
同位角
一、同位角的概念
A
A.(1),(2) B.(3),(4)
C.(1),(2),(3) D.(2),(3) ,(3)
例1:下列图形中,∠1和∠2是同位角的有( )
1
2
1
2
1
2
1
2
(1) (2) (3) (4)
图形特征:在形如字母“F”的图形中有同位角.
变式图形:图中的∠1与∠2都是同位角.
1
2
1
2
1
2
1
2
A
C
B
D
E
F
1
2
3
4
5
6
7
8
活动2 观察∠3与∠5的位置关系:
①在直线EF的两侧
②在直线AB、CD之间
3
5
∠4和∠6
图中的内错角还有哪些?
内错角
二、内错角的概念
例2:如图,与∠1是内错角的是( )
1
3
2
4
5
A. ∠2 B. ∠3
C. ∠4 D. ∠5
B
变式图形:图中的∠1与∠2都是内错角.
图形特征:在形如“Z”的图形中有内错角.
1
2
1
1
1
2
2
2
A
C
B
D
E
F
1
2
3
4
5
6
7
8
活动3 观察∠4与∠5的位置关系
①在直线EF的同旁
②在直线AB、CD之间
4
5
∠3和∠6
图中还有哪些同旁内角?
同旁内角
三、同旁内角的概念
例3:下列图形中,∠1和∠2是同旁内角的有( )
1
1
A
B
C
D
1
2
2
2
1
2
A
变式图形:图中的∠1与∠2都是同旁内角.
图形特征:在形如“U”的图形中有同旁内角.
1
1
1
1
2
2
2
2
同位角、内错角和同旁内角的结构特征:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}角的
名称
角的特征
基本图形
基本图形
相同点
共同特征
同位角
同旁
内角
内错角
F
Z
U
截线:同侧
被截线:同旁
截线:同侧
被截线:之间
截线:两侧
被截线:之间
1
2
1
2
1
2
都在截线同侧
都在被截线之间
这三类角都是没有公共顶点的.
总结归纳
例4 如图,直线DE截AB ,AC,构成8个角,指出所有的同位角,内错角,同旁内角.
解:两条直线是AB,AC,截线是DE,所以8个角中,同位角:∠2与∠5,∠4与∠7,∠1与∠8, ∠6和∠3;内错角:∠4与∠5,∠1与∠6;同旁内角:∠1与∠5,∠4与∠6.
E
D
C
B
A
8
7
6
5
4
3
2
1
变式:∠A与∠8是哪两条直线被哪条直线所截的角?它们是什么关系的角?∠A与∠5呢?∠A与∠6呢?
E
D
C
B
A
8
7
6
5
4
3
2
1
解:∠A与∠8是直线AB,DE被直线AC所截形成的内错角.
∠A与∠5是直线AB,DE被直线AC所截形成的同旁内角.
∠A与∠6是直线AB,DE被直线AC所截形成的同位角.
练一练:识别这些角是同位角、内错角还是同旁内角
1
2
(1)
同位角
1
2
(2)
1
2
(3)
1
2
(4)
1
2
(5)
1
2
(6)
1
2
(7)
1
2
(8)
1
2
1
2
(9)
(10)
同位角
同位角
同位角
同位角
内错角
同旁内角
例5 如图,直线DE,BC被直线AB所截.
(1)∠1与∠2, ∠1和∠3,∠1和∠4各是什么角?
4
3
2
1
F
E
D
C
B
A
解:(1)∠1与∠2是内错角,∠1和∠3同旁内角,∠1和∠4是同位角.
温馨提示:解题之前要明确哪两条直线被哪条直线所截.
解:(2)如果∠1=∠4,由对顶角相等,得∠2=∠4,那么∠1=∠2.因为∠3和∠4互补,即∠4+∠3=180°,又因为∠1=∠4,所以∠1+∠3=180°,即∠1与∠3互补.
4
3
2
1
F
E
D
C
B
A
(2)如果∠1=∠4,那么∠1与∠2相等吗?∠1与
∠3互补吗? 为什么?
生活中的数学:三线八角手势记忆法
同位角
内错角
同旁内角
小 结
2、掌握辩别这些角的关键是看哪两条直线被哪一条直线所截、分清哪一条直线截哪两条直线形成了哪些角,是作出正确判定的前提,在截线的同旁找同位角,同旁内角,在截线的不同旁,找内错角.
1、同位角、内错角、同旁内角都是两条直线被第三条直线所截时产生的,我们要掌握他们的位置特征.
【课后练习】
1.在我们常见的英文字母中,也存在着同位角、内错角、同旁内角.在下面几个字母中,含有内错角最少的字母是( )
A.H B.M C.N D.A
2.平面上三条直线两两相交最多能构成对顶角的对数是( ).
A.7 B.6 C.5 D.4
3.下列说法中,正确的是( )
A.相等的两个角是对顶角
B.有一条公共边的两个角是邻补角
C.有公共顶点的两个角是对顶角
D.一条直线与端点在这条直线上的一条射线组成的两个角是邻补角
4.若∠A与∠B是对顶角且互补,则它们两边所在的直线( )
A.互相垂直 B.互相平行
C.既不垂直也不平行 D.不能确定
5.已知∠1与∠2是同旁内角,若∠1=50°,则∠2的度数是( )
A.130° B.50° C.100° D.不能确定
6.如图,两只手的食指和拇指在同一个平面内,它们构成的一对角可看成是( )
A.同位角 B.内错角 C.对顶角 D.同旁内角
7.若∠1与∠2是同位角,则它们之间的关系是( ).
A.∠1=∠2 ; B.∠1>∠2 ;
C.∠1<∠2; D.∠1=∠2或∠1>∠2或∠1<∠2.
8.在我们常见的英文字母中,存在着同位角、内错角、同旁内角的现象.在下列几个字母中,不含同旁内角现象的字母是( )
A.E B.F C.N D.H
9.下列命题中正确的有( )个.
①=a;②同位角相等;③过一点有且只有一条直线垂直于已知直线;④一个数的平方根等于它本身,这个数是0和1;⑤经过直线外一点有且只有一条直线与这条直线平行.
A.1 B.2 C.3 D.4
10.若∠A与∠B是对顶角且互补,则它们两边所在的直线( )
A.互相垂直 B.互相平行 C.既不垂直也不平行 D.不能确定
11..四条直线两两相交,且任意三条直线不相交于同点,则四条直线共可构成的同位角有________对.
12.若∠1与∠2是对顶角,且∠1与∠2互余,则∠1=________,∠2=________.
13.两条直线相交所成的四个角中,有两个角分别是(2x-10)°和(110-x)°,则x=_____.
14.探究题:
(1)三条直线相交,最少有__________个交点,最多有__________个交点,分别画出图形,并数出图形中的对顶角和邻补角的对数;
(2)四条直线相交,最少有__________个交点,最多有__________个交点,分别画出图形,并数出图形中的对顶角和邻补角的对数;
(3)依次类推,n条直线相交,最少有__________个交点,最多有__________个交点,对顶角有_________对,邻补角有__________对.
15.如图,在直线DE与∠O的两边相交,则∠O的同位角是_______,∠8的内错角是_______,∠1的同旁内角是_______.
【课后练习】答案
1.C 2.B 3.D 4.A 5.D 6.B 7.D 8.C 9.A 10.A
11.48
12. 45°, 45°
13.40或80
14.(1)1,3;(2)1,6;(3)1, ,n(n-1),2n(n-1)
15.∠2和∠5;∠2;∠8和∠O
