人教版七年级下册 7.2.2 用坐标表示平移课件(16张PPT)
文档属性
| 名称 | 人教版七年级下册 7.2.2 用坐标表示平移课件(16张PPT) |
|
|
| 格式 | ppt | ||
| 文件大小 | 355.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-19 00:00:00 | ||
图片预览






文档简介
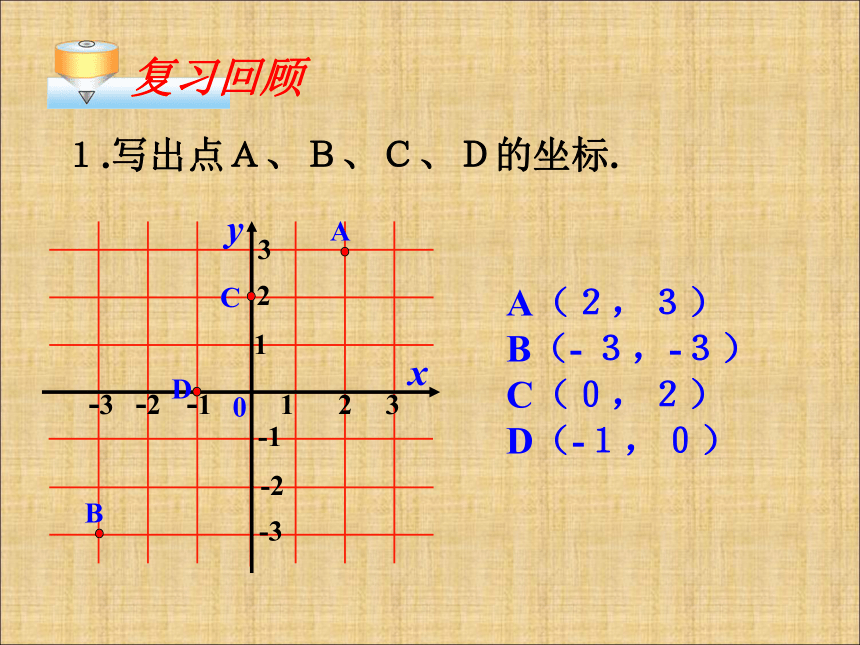
复习回顾
-3
-2
-1
0
1
2
3
x
y
1
3
2
-2
-1
-3
A
B
D
C
1.写出点A、B、C、D的坐标.
A(2,3) B(- 3,-3) C(0,2)
D(-1,0)
2.下列各点分别在坐标平面的什么位置上?
A(3,2)
B(0,-2)
C(-3,-2)
D(-3,0)
E(-1.5,3.5)
F(2,-3)
第一象限
第三象限
第二象限
第四象限
y轴上
x轴上
(+ , +)
(- , +)
(- , -)
(+ , -)
(0 , y)
(x, 0)
每个象限内的点都有自已的符号特征.
3. 角平分线上的点的坐标有何特点?
一、三象限夹角平分线上的点的
横、纵坐标 ;
二、四象限夹角平分线上的点的
横、纵坐标 。
相等
互为相反数
4. 平行于坐标轴的直线上的点的坐标有何特点?
平行于y轴的直线上的点的横坐标相同,
平行于x轴的直线上的点的纵坐标相同。
5. 平面上任一点到坐标轴的距离怎么求?
P(a,b)
到x轴的距离是_____
到y轴的距离是_____
︱b︱;
︱a︱;
用坐标表示平移
探究
A
1
3
5
2
4
6
-1
-2
-3
-4
-5
-6
0
E
3
4
2
-1
5
-2
-3
-4
-6
-5
6
0
1
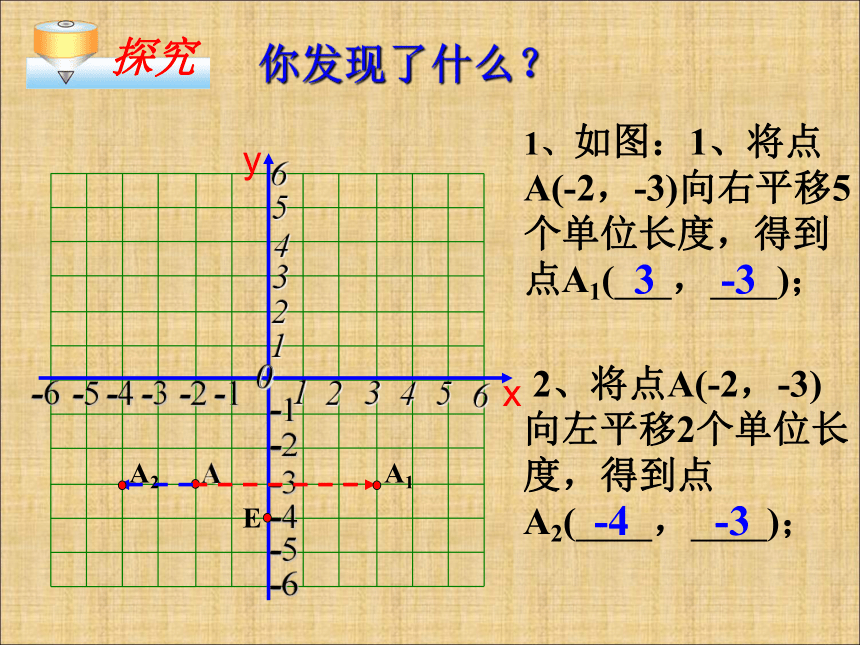
1、如图:1、将点A(-2,-3)向右平移5个单位长度,得到点A1( , );
2、将点A(-2,-3)向左平移2个单位长度,得到点A2( , );
A1
-4
-3
3
-3
A2
你发现了什么?
y
x
探究
A
1
3
5
2
4
6
-1
-2
-3
-4
-5
-6
0
E
3
4
2
-1
5
-2
-3
-4
-6
-5
6
0
1
3、将点A(-2,-3)向上平移4个单位长度,得到点A3( , );
4、将点A(-2,-3)向下平移2个单位长度,得到点A4( , ).
A3
A4
-2
1
-2
-5
你发现了什么?
x
y
2、将点(x,y)向上(或下)平移b个单位长度,可以得到对应点(x ,y +b)或 ( , ).
1、将点(x,y)向右(或左)平移a个单位长度,可以得到对应点(x+a,y)或( , ).
归纳
在平面直角坐标系中,
x - a
y
x
y -b
左、右平移纵坐标不变,横坐标变,变化规律是左减右加;
一个图形在平面直角坐标系中进行平移,其坐标就要发生相应的变化, 可以简单地理解为:
例如:当P(x ,y)向右平移a个单位长度,再向上平移b个单位长度后坐标为p′(x+a ,y+b).
上下平移横坐标不变,纵坐标变,变化规律是上加下减.
探究
我来试一试
已知点A(-2,-3):
1、(1)将点A向右平移5个单位长度得到点A1,则 点A1点的坐标是 ;
(2)将点A向右平移6个单位长度得到点A2,则 点A2点的坐标是 ;
(3)将点A向右平移a(a>o)个单位长度得到点An,则 点An点的坐标是 ;
(4)将点A向左平移a(a>o)个单位长度得到点An ′ ,则 点An ′点的坐标是 ;
(-2-a ,-3)
(3,-3)
(4,-3)
(-2+ a ,-3)
2、如图,将三角形ABC向左平移2个单位长度在向下平移3个单位长度,则A、B、C各点的坐标变为多少?
A
B
C
-4
-5
1
2
3
4
1
2
3
4
-1
-2
-3
-1
-2
-3
o
x
y
0
A1(1,-1)
B1(-1,-4)
C1(3,-5)
A
B
C
-4
-5
1
2
3
4
1
2
3
4
-1
-2
-3
-1
-2
-3
o
x
y
(-3,2)
(-2,-1)
(3,0)
3、如图,三角形ABC上任意一点P(x0,y0)经平移后得到的对应点为P1(x0+2,y0+4),将三角形ABC作同样的平移得到三角形A1B1C1.求A1、B1、C1的坐标.
P(x0,y0)
P1(x0+2,y0+4)
B
C
B1
A1
C1
B
A
C
观察下列图形,与图(1)的鱼相比,图(2)中的鱼发生了一些变化,若图(1)中鱼上P点的坐标为(4,3.2)则这个点在图(2)中的对应点P的坐标应为_______;
课后思考
y
1
1
-1
-2
-3
2
3
4
4
5
3
2
O
1
1
-1
-2
-3
2
3
4
4
5
3
2
O
图1
图2
P
●
P
●
ⅹ
ⅹ
y
(4,2.2)
1
2
3
4
5
-4
-3
-2
-1
·
O
X
P(3,2)
·
B(3,-2)
A(-3,2)
C(-3,- 2 )
·
·
你能说出点P关于x轴、y轴、原点的对称点坐标吗?
·
3
1
4
2
5
-2
-4
-1
-3
y
若设点M(a,b),
M点关于X轴的对称点M1( )
M点关于Y轴的对称点M2( ),
M点关于原点O的对称点M3( )
a,-b
- a, b
-a,-b
练一练
-3
-2
-1
0
1
2
3
x
y
1
3
2
-2
-1
-3
A
B
D
C
1.写出点A、B、C、D的坐标.
A(2,3) B(- 3,-3) C(0,2)
D(-1,0)
2.下列各点分别在坐标平面的什么位置上?
A(3,2)
B(0,-2)
C(-3,-2)
D(-3,0)
E(-1.5,3.5)
F(2,-3)
第一象限
第三象限
第二象限
第四象限
y轴上
x轴上
(+ , +)
(- , +)
(- , -)
(+ , -)
(0 , y)
(x, 0)
每个象限内的点都有自已的符号特征.
3. 角平分线上的点的坐标有何特点?
一、三象限夹角平分线上的点的
横、纵坐标 ;
二、四象限夹角平分线上的点的
横、纵坐标 。
相等
互为相反数
4. 平行于坐标轴的直线上的点的坐标有何特点?
平行于y轴的直线上的点的横坐标相同,
平行于x轴的直线上的点的纵坐标相同。
5. 平面上任一点到坐标轴的距离怎么求?
P(a,b)
到x轴的距离是_____
到y轴的距离是_____
︱b︱;
︱a︱;
用坐标表示平移
探究
A
1
3
5
2
4
6
-1
-2
-3
-4
-5
-6
0
E
3
4
2
-1
5
-2
-3
-4
-6
-5
6
0
1
1、如图:1、将点A(-2,-3)向右平移5个单位长度,得到点A1( , );
2、将点A(-2,-3)向左平移2个单位长度,得到点A2( , );
A1
-4
-3
3
-3
A2
你发现了什么?
y
x
探究
A
1
3
5
2
4
6
-1
-2
-3
-4
-5
-6
0
E
3
4
2
-1
5
-2
-3
-4
-6
-5
6
0
1
3、将点A(-2,-3)向上平移4个单位长度,得到点A3( , );
4、将点A(-2,-3)向下平移2个单位长度,得到点A4( , ).
A3
A4
-2
1
-2
-5
你发现了什么?
x
y
2、将点(x,y)向上(或下)平移b个单位长度,可以得到对应点(x ,y +b)或 ( , ).
1、将点(x,y)向右(或左)平移a个单位长度,可以得到对应点(x+a,y)或( , ).
归纳
在平面直角坐标系中,
x - a
y
x
y -b
左、右平移纵坐标不变,横坐标变,变化规律是左减右加;
一个图形在平面直角坐标系中进行平移,其坐标就要发生相应的变化, 可以简单地理解为:
例如:当P(x ,y)向右平移a个单位长度,再向上平移b个单位长度后坐标为p′(x+a ,y+b).
上下平移横坐标不变,纵坐标变,变化规律是上加下减.
探究
我来试一试
已知点A(-2,-3):
1、(1)将点A向右平移5个单位长度得到点A1,则 点A1点的坐标是 ;
(2)将点A向右平移6个单位长度得到点A2,则 点A2点的坐标是 ;
(3)将点A向右平移a(a>o)个单位长度得到点An,则 点An点的坐标是 ;
(4)将点A向左平移a(a>o)个单位长度得到点An ′ ,则 点An ′点的坐标是 ;
(-2-a ,-3)
(3,-3)
(4,-3)
(-2+ a ,-3)
2、如图,将三角形ABC向左平移2个单位长度在向下平移3个单位长度,则A、B、C各点的坐标变为多少?
A
B
C
-4
-5
1
2
3
4
1
2
3
4
-1
-2
-3
-1
-2
-3
o
x
y
0
A1(1,-1)
B1(-1,-4)
C1(3,-5)
A
B
C
-4
-5
1
2
3
4
1
2
3
4
-1
-2
-3
-1
-2
-3
o
x
y
(-3,2)
(-2,-1)
(3,0)
3、如图,三角形ABC上任意一点P(x0,y0)经平移后得到的对应点为P1(x0+2,y0+4),将三角形ABC作同样的平移得到三角形A1B1C1.求A1、B1、C1的坐标.
P(x0,y0)
P1(x0+2,y0+4)
B
C
B1
A1
C1
B
A
C
观察下列图形,与图(1)的鱼相比,图(2)中的鱼发生了一些变化,若图(1)中鱼上P点的坐标为(4,3.2)则这个点在图(2)中的对应点P的坐标应为_______;
课后思考
y
1
1
-1
-2
-3
2
3
4
4
5
3
2
O
1
1
-1
-2
-3
2
3
4
4
5
3
2
O
图1
图2
P
●
P
●
ⅹ
ⅹ
y
(4,2.2)
1
2
3
4
5
-4
-3
-2
-1
·
O
X
P(3,2)
·
B(3,-2)
A(-3,2)
C(-3,- 2 )
·
·
你能说出点P关于x轴、y轴、原点的对称点坐标吗?
·
3
1
4
2
5
-2
-4
-1
-3
y
若设点M(a,b),
M点关于X轴的对称点M1( )
M点关于Y轴的对称点M2( ),
M点关于原点O的对称点M3( )
a,-b
- a, b
-a,-b
练一练
