人教版数学七年级下册课件:6.1平方根(第3课时)(19张PPT)
文档属性
| 名称 | 人教版数学七年级下册课件:6.1平方根(第3课时)(19张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 231.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-19 00:00:00 | ||
图片预览






文档简介
(1)什么是算术平方根?怎样表示?
如果一个正数x的平方等于a,那么这个正数x叫做a的算术平方根.
a的算术平方根表示为:
(2)下列各式有意义的条件是什么?
(3)如果一个数的平方等于9,那么这个数是多少?
6.1 平方根
(第3课时)
自学课本P44—46练习前,思考:
1、填写P45页表格,理解什么叫平方根?怎样表示一个数的平方根?
2、什么叫开平方?它与平方运算有什么关系?
3、正数的平方根有什么特点?0的平方根是多少?负数有平方根吗?
4, 掌握例4例5的解题格式和步骤,思考平方根和算术平方根有什么区别与联系?
5、完成P45-47页练习
填表:
如果我们把 分别叫做
的平方根,你能类比算术
平方根的概念,给出平方根的概念吗?
如果一个数的平方等于a,那么这个数就叫做a的_______或_______.
即 =a时x叫做a的平方根,记作x=____.
温馨提示:符号 只有当________时有意义,________时无意义.
求一个数的平方根的运算,叫做_ __;平方与开平方互为 ____运算.
平方根
二次方根
a≥0
a<0
开平方
逆
1、判断下列说法是否正确:
(1)0的平方根是0;( )
(2)1的平方根是1;( )
(3)-1的平方根是-1( )
(4)0.01是0.1的一个平方根。( )
√
×
×
×
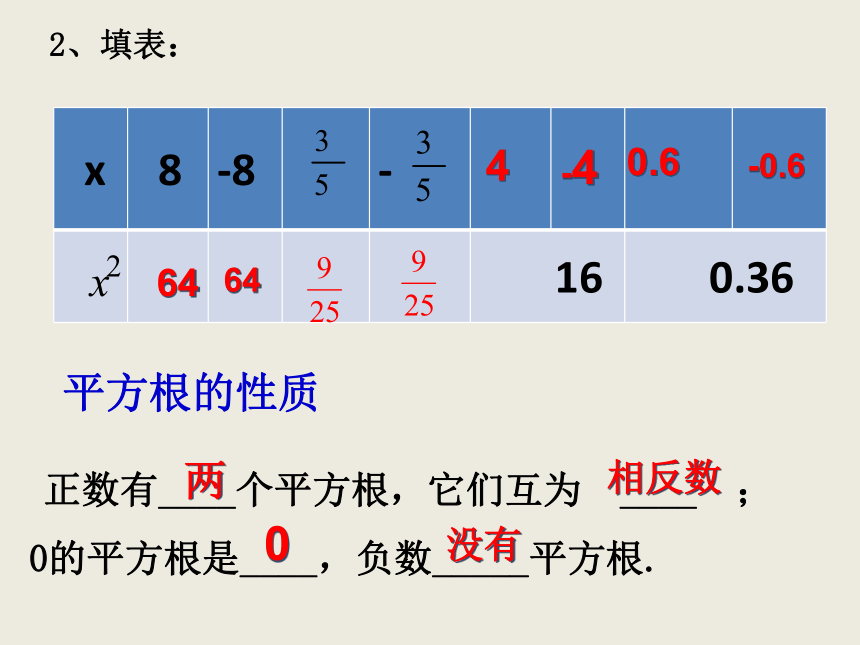
2、填表:
x
8
-8
-
16
0.36
64
64
4
-4
0.6
-0.6
正数有____个平方根,它们互为 ____ ;
0的平方根是____,负数_____平方根.
两
相反数
0
没有
平方根的性质
计算下列各式的值;
(1) (2)- (3)
解:
=
3
-
=
-
±
=
±
平方根和算术平方根
1、联系:(1)具有包含关系:__ __包含算术平方根,__ __ 是平方根的一种.
(2)存在条件相同:平方根和算术平方根都是只有______数才有.
(3)0的平方根、算术平方根都是___.
2、区别:(1)定义不同:“如果一个____的平方等于a,这个数就叫做a的平方根” ; “非负数a的非负平方根叫a的 ____________”.
(2)个数不同:一个正数有___个平方根,而一个正数的算术平方根只有____个.
(3)表示法不同:正数a的平方根表示为____,正数的算术平方根表示为___ .
平方根
算术平方根
非负
0
数
算术平方根
两
一
±
(3)如果一个数的平方等于9,那么这个数是多少?
解决问题
1. 判断下列各式计算是否正确,并说明理由.
2.判断下列说法是否正确,并说明理由.
(1)49的平方根是7;
(2)2是4的平方根;
(3)64的平方根是 8 ;
×
±7
√
√
3. 说出下列各式的意义,并求它们的值:
解:(1) ;
(2) ;
(3) .
5、已知 m 的平方根是 2a-3 和 a-12,
求 a和m 的值。
4、若 25x2-36 = 0, 则 x = ;
若 (2x)2 = 0.36, 则 x = ;
6、若 求ab的值。
四、归纳小结
1、如果_____________等于a,那么这个数就叫做的平方根或二次方根;
2、非负数a的平方根表示为______.
3、± 中的a称为___ 数,其中有意义的条件是_______;
4、一个正数有____个平方根,它们互为_____;0的平方根是___,负数______平方根.
5、平方根与算术平方根的联系与区别?
一个数的平方
0
±
被开方
a≥0
两
相反数
没有
一种思想
两种语言
一个定义
三条性质
1+2+3+1
1、判断下列各数是否有平方根?说明理由。
(1) (2) 0 (3) -0.01 (4)-
2、填空
(1)25的平方根是____; (2)± =____;
(3)- =_______
(4) 的平方根是_____,算术平方根是____.
有
有
没有
不一定
±5
±13
-
±2
2
5、平方根概念的起源与几何中的正方形有关,如果一个正方形的面积为A,那么这个正方形的边长是多少?
解:设正方形的边长为x,则x2=A,
X=
A组:绩优学案P38页,
课本P47-48页3、 4、 8、 9题.
B组:绩优学案P38页,
课本P47-48页3、 4、 8题 .
作业布置
如果一个正数x的平方等于a,那么这个正数x叫做a的算术平方根.
a的算术平方根表示为:
(2)下列各式有意义的条件是什么?
(3)如果一个数的平方等于9,那么这个数是多少?
6.1 平方根
(第3课时)
自学课本P44—46练习前,思考:
1、填写P45页表格,理解什么叫平方根?怎样表示一个数的平方根?
2、什么叫开平方?它与平方运算有什么关系?
3、正数的平方根有什么特点?0的平方根是多少?负数有平方根吗?
4, 掌握例4例5的解题格式和步骤,思考平方根和算术平方根有什么区别与联系?
5、完成P45-47页练习
填表:
如果我们把 分别叫做
的平方根,你能类比算术
平方根的概念,给出平方根的概念吗?
如果一个数的平方等于a,那么这个数就叫做a的_______或_______.
即 =a时x叫做a的平方根,记作x=____.
温馨提示:符号 只有当________时有意义,________时无意义.
求一个数的平方根的运算,叫做_ __;平方与开平方互为 ____运算.
平方根
二次方根
a≥0
a<0
开平方
逆
1、判断下列说法是否正确:
(1)0的平方根是0;( )
(2)1的平方根是1;( )
(3)-1的平方根是-1( )
(4)0.01是0.1的一个平方根。( )
√
×
×
×
2、填表:
x
8
-8
-
16
0.36
64
64
4
-4
0.6
-0.6
正数有____个平方根,它们互为 ____ ;
0的平方根是____,负数_____平方根.
两
相反数
0
没有
平方根的性质
计算下列各式的值;
(1) (2)- (3)
解:
=
3
-
=
-
±
=
±
平方根和算术平方根
1、联系:(1)具有包含关系:__ __包含算术平方根,__ __ 是平方根的一种.
(2)存在条件相同:平方根和算术平方根都是只有______数才有.
(3)0的平方根、算术平方根都是___.
2、区别:(1)定义不同:“如果一个____的平方等于a,这个数就叫做a的平方根” ; “非负数a的非负平方根叫a的 ____________”.
(2)个数不同:一个正数有___个平方根,而一个正数的算术平方根只有____个.
(3)表示法不同:正数a的平方根表示为____,正数的算术平方根表示为___ .
平方根
算术平方根
非负
0
数
算术平方根
两
一
±
(3)如果一个数的平方等于9,那么这个数是多少?
解决问题
1. 判断下列各式计算是否正确,并说明理由.
2.判断下列说法是否正确,并说明理由.
(1)49的平方根是7;
(2)2是4的平方根;
(3)64的平方根是 8 ;
×
±7
√
√
3. 说出下列各式的意义,并求它们的值:
解:(1) ;
(2) ;
(3) .
5、已知 m 的平方根是 2a-3 和 a-12,
求 a和m 的值。
4、若 25x2-36 = 0, 则 x = ;
若 (2x)2 = 0.36, 则 x = ;
6、若 求ab的值。
四、归纳小结
1、如果_____________等于a,那么这个数就叫做的平方根或二次方根;
2、非负数a的平方根表示为______.
3、± 中的a称为___ 数,其中有意义的条件是_______;
4、一个正数有____个平方根,它们互为_____;0的平方根是___,负数______平方根.
5、平方根与算术平方根的联系与区别?
一个数的平方
0
±
被开方
a≥0
两
相反数
没有
一种思想
两种语言
一个定义
三条性质
1+2+3+1
1、判断下列各数是否有平方根?说明理由。
(1) (2) 0 (3) -0.01 (4)-
2、填空
(1)25的平方根是____; (2)± =____;
(3)- =_______
(4) 的平方根是_____,算术平方根是____.
有
有
没有
不一定
±5
±13
-
±2
2
5、平方根概念的起源与几何中的正方形有关,如果一个正方形的面积为A,那么这个正方形的边长是多少?
解:设正方形的边长为x,则x2=A,
X=
A组:绩优学案P38页,
课本P47-48页3、 4、 8、 9题.
B组:绩优学案P38页,
课本P47-48页3、 4、 8题 .
作业布置
