人教数学八年下册18.1.1 平行四边形的性质教学课件(共17张PPT)
文档属性
| 名称 | 人教数学八年下册18.1.1 平行四边形的性质教学课件(共17张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-19 00:00:00 | ||
图片预览






文档简介
平行四边形及其性质(一)
学习目标:
1.理解平行四边形的概念;
2.探索并掌握平行四边形对边相等、对角相等的性质;
3.初步体会几何研究的一般思路与方法。
学习重点:
平行四边形边角性质的证明和应用。
两组对边都不平行
一组对边平行,
一组对边不平行
两组对边分别平行
四边形
平行四边形
有两组对边分别平行的四边形叫做平行四边形。
观察图形,说出下列图形边的位置有什么特征?
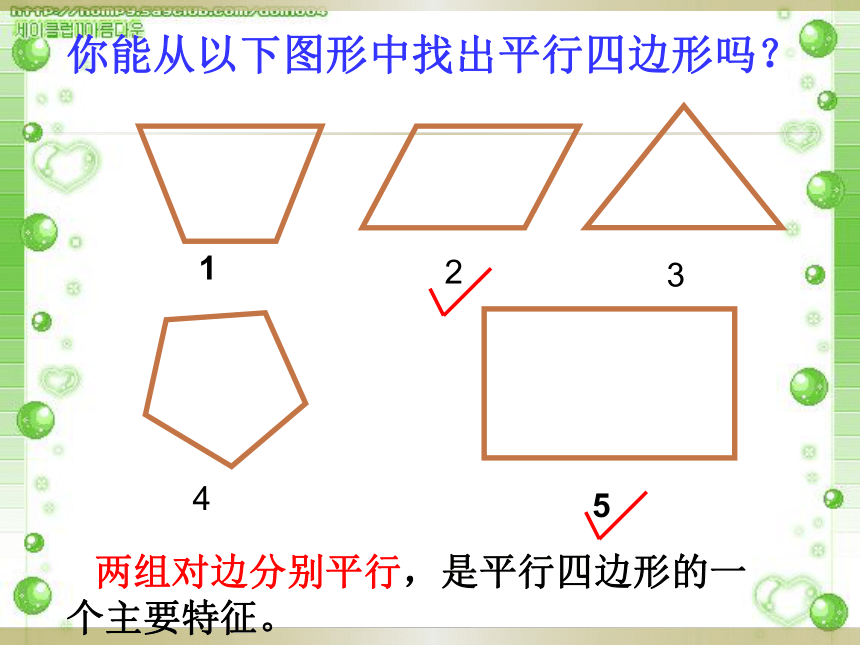
你能从以下图形中找出平行四边形吗?
两组对边分别平行,是平行四边形的一个主要特征。
2
3
1
4
5
平行四边形相对的边称为 对边
相对的角称为 对角
如图:线段AC、BD就是 ABCD的对角线
A
D
C
B
平行四边形不相邻的两个顶点连成的线段叫平行四边形的对角线.
1.两组对边分别平行的四边形叫做平行四边形.
如图:四边形ABCD是平行四边形
记作: ABCD
读作:平行四边形ABCD
∵ AB ∥ CD,BC ∥ AD,
∴四边形ABCD是平行四边形。
如图,DC∥ EF ∥ AB,DA∥ GH∥ CB,图中的平行四边形有__个,它们是_______________________________________________
讨 论
9
AHOE
ABCD
BHGC
AHGD
CDEF
ABFE
CFOG
DEOG
BHOF
对于平行四边形,从定义出发,你能得出它的性质
吗?
你能证明这些结论吗?
概括证明,探究性质
给出图形定义→研究图形性质→探索图形判定条件
回忆我们的学习经历,研究几何图形的一般思路是
什么?
猜想:平行四边形对角相等,对边相等。
概括证明,探究性质
归纳:
(1)有关四边形的问题常常转化为三角形问题解决;
(2)平行四边形的一条对角线把平行四边形分成两个全 等的三角形;
A
B
C
D
概括证明,探究性质
归纳:
(3)平行四边形的性质定理:平行四边形的对边相等,平行四边形的对角相等。
∵四边形ABCD是平行四边形(已知),
∴AB=CD,AD=BC(平行四边形的性质);
∠DAB=∠DCB,∠B=∠D(平行四边形的性质)。
A
B
C
D
性质2:平行四边形的对角相等。
性质1:平行四边形的对边平行
且相等。
思考:平行四边形中相邻的两角有什么关系呢
E
F
G
H
邻角互补。
解:
∵四边形ABCD是平行四边形
且∠A=52°(已知)
∴ ∠A=∠C=52°(平行四边形的对角相等)
又∵AD∥BC(平行四边形的对边平行)
∴∠A+∠B=180°(两直线平行,同旁内角互补)
∴∠B=∠D= 180 °-∠A= 180?- 52°=128 °
在 ABCD中,已知∠A=52 ° ,求其余三个角的度数。
A
B
C
D
52°
例
题
教
学
如图: 在 ABCD中,∠A+∠C=200°
则:∠A= ,∠B= .
变式练习:
A
D
B
C
100 °
80 °
解:
∴∠B= 180 °-∠A= 180?- 100°=80°
又∵AD∥BC(平行四边形的对边平行)
∵四边形ABCD是平行四边形
∴∠A=∠C=100 ° (平行四边形的对角相等)
且∠A+∠C=200°
可要细心哟
在 ABCD 中, ∠A与∠B 的度数之比为4:5,∠A= , ∠B= , ∠C= ∠D= 。
A
B
C
D
80°
100°
80°
100°
在平行四边形ABCD中,若AE平分∠DAB,AB=5cm,AD=9cm,则EC= .
C
4cm
A
B
D
E
9cm
1
2
5cm
9cm
3
学习目标:
1.理解平行四边形的概念;
2.探索并掌握平行四边形对边相等、对角相等的性质;
3.初步体会几何研究的一般思路与方法。
学习重点:
平行四边形边角性质的证明和应用。
两组对边都不平行
一组对边平行,
一组对边不平行
两组对边分别平行
四边形
平行四边形
有两组对边分别平行的四边形叫做平行四边形。
观察图形,说出下列图形边的位置有什么特征?
你能从以下图形中找出平行四边形吗?
两组对边分别平行,是平行四边形的一个主要特征。
2
3
1
4
5
平行四边形相对的边称为 对边
相对的角称为 对角
如图:线段AC、BD就是 ABCD的对角线
A
D
C
B
平行四边形不相邻的两个顶点连成的线段叫平行四边形的对角线.
1.两组对边分别平行的四边形叫做平行四边形.
如图:四边形ABCD是平行四边形
记作: ABCD
读作:平行四边形ABCD
∵ AB ∥ CD,BC ∥ AD,
∴四边形ABCD是平行四边形。
如图,DC∥ EF ∥ AB,DA∥ GH∥ CB,图中的平行四边形有__个,它们是_______________________________________________
讨 论
9
AHOE
ABCD
BHGC
AHGD
CDEF
ABFE
CFOG
DEOG
BHOF
对于平行四边形,从定义出发,你能得出它的性质
吗?
你能证明这些结论吗?
概括证明,探究性质
给出图形定义→研究图形性质→探索图形判定条件
回忆我们的学习经历,研究几何图形的一般思路是
什么?
猜想:平行四边形对角相等,对边相等。
概括证明,探究性质
归纳:
(1)有关四边形的问题常常转化为三角形问题解决;
(2)平行四边形的一条对角线把平行四边形分成两个全 等的三角形;
A
B
C
D
概括证明,探究性质
归纳:
(3)平行四边形的性质定理:平行四边形的对边相等,平行四边形的对角相等。
∵四边形ABCD是平行四边形(已知),
∴AB=CD,AD=BC(平行四边形的性质);
∠DAB=∠DCB,∠B=∠D(平行四边形的性质)。
A
B
C
D
性质2:平行四边形的对角相等。
性质1:平行四边形的对边平行
且相等。
思考:平行四边形中相邻的两角有什么关系呢
E
F
G
H
邻角互补。
解:
∵四边形ABCD是平行四边形
且∠A=52°(已知)
∴ ∠A=∠C=52°(平行四边形的对角相等)
又∵AD∥BC(平行四边形的对边平行)
∴∠A+∠B=180°(两直线平行,同旁内角互补)
∴∠B=∠D= 180 °-∠A= 180?- 52°=128 °
在 ABCD中,已知∠A=52 ° ,求其余三个角的度数。
A
B
C
D
52°
例
题
教
学
如图: 在 ABCD中,∠A+∠C=200°
则:∠A= ,∠B= .
变式练习:
A
D
B
C
100 °
80 °
解:
∴∠B= 180 °-∠A= 180?- 100°=80°
又∵AD∥BC(平行四边形的对边平行)
∵四边形ABCD是平行四边形
∴∠A=∠C=100 ° (平行四边形的对角相等)
且∠A+∠C=200°
可要细心哟
在 ABCD 中, ∠A与∠B 的度数之比为4:5,∠A= , ∠B= , ∠C= ∠D= 。
A
B
C
D
80°
100°
80°
100°
在平行四边形ABCD中,若AE平分∠DAB,AB=5cm,AD=9cm,则EC= .
C
4cm
A
B
D
E
9cm
1
2
5cm
9cm
3
