2020-2021学年北京版五年级下册数学《第二单元 折线统计图与可能性》单元达标检测卷(有答案)
文档属性
| 名称 | 2020-2021学年北京版五年级下册数学《第二单元 折线统计图与可能性》单元达标检测卷(有答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 314.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-19 00:00:00 | ||
图片预览



文档简介
2020-2021学年北京课改版五年级下册数学《第二单元
折线统计图与可能性》单元达标检测卷
一.选择题(共8小题)
1.如图是小明每天上学走的路程统计图,那么他从家到学校需要走( )千米.
A.5
B.2.5
C.10
2.妈妈早上去上班,走了一半的路程想起把文件忘在家里了,然后返回家取文件,再去上班,下班后直接回家,下面的
( )图反映出妈妈上班和下班离家距离的情况.
A.
B.
C.
D.
3.龟兔赛跑是我们非常熟悉的故事,故事大意是:乌龟和兔子赛跑,兔子开始就领先了乌龟很多,兔子不耐烦了,就在路边睡了一觉,而乌龟一直往目的地奔跑,最终乌龟获得了胜利.下面能反映这个故事情节的图是( )
A.
B.
C.
D.
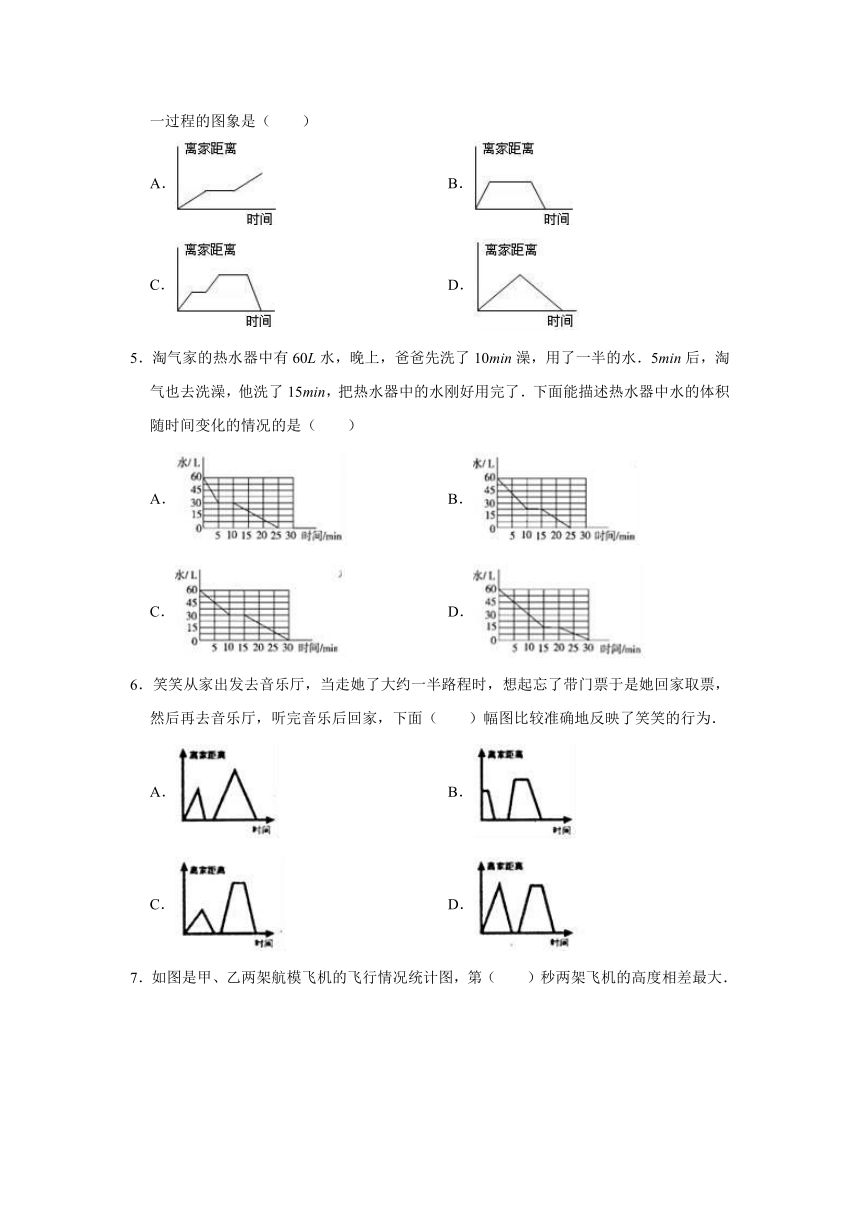
4.淘气从家去书城,中途休息了几分钟,到书城买完书后直接回家.下面正确描述淘气这一过程的图象是( )
A.
B.
C.
D.
5.淘气家的热水器中有60L水,晚上,爸爸先洗了10min澡,用了一半的水.5min后,淘气也去洗澡,他洗了15min,把热水器中的水刚好用完了.下面能描述热水器中水的体积随时间变化的情况的是( )
A.
B.
C.
D.
6.笑笑从家出发去音乐厅,当走她了大约一半路程时,想起忘了带门票于是她回家取票,然后再去音乐厅,听完音乐后回家,下面( )幅图比较准确地反映了笑笑的行为.
A.
B.
C.
D.
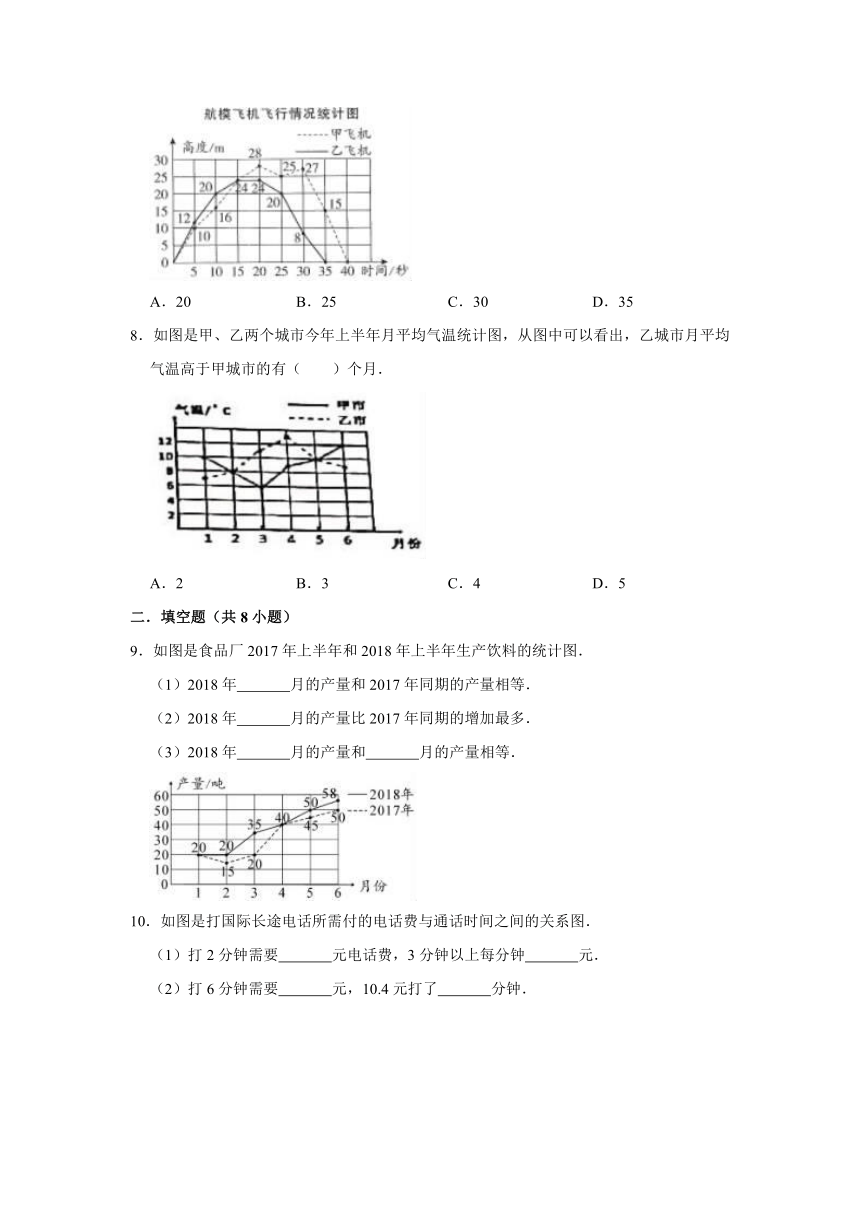
7.如图是甲、乙两架航模飞机的飞行情况统计图,第( )秒两架飞机的高度相差最大.
A.20
B.25
C.30
D.35
8.如图是甲、乙两个城市今年上半年月平均气温统计图,从图中可以看出,乙城市月平均气温高于甲城市的有( )个月.
A.2
B.3
C.4
D.5
二.填空题(共8小题)
9.如图是食品厂2017年上半年和2018年上半年生产饮料的统计图.
(1)2018年
月的产量和2017年同期的产量相等.
(2)2018年
月的产量比2017年同期的增加最多.
(3)2018年
月的产量和
月的产量相等.
10.如图是打国际长途电话所需付的电话费与通话时间之间的关系图.
(1)打2分钟需要
元电话费,3分钟以上每分钟
元.
(2)打6分钟需要
元,10.4元打了
分钟.
11.下面是小明某天从家出发到山区的行车情况统计图.
小明某天外出行车情况统计图
(1)小明共行驶了
千米.
(2)小明出发后,经过
小时到达了目的地,途中休息了
小时.
(3)不算休息,小明平均每小时行驶
千米.
12.如图是某超市第一分店、第二分店上半年营业额情况统计图.
(1)第
分店营业额更高.
(2)
月份至
月份第一分店营业额下降得最快.
(3)
月份两个店营业额比较接近;
月份相差较远.
(4)
月份到
月份两店的营业额都是增长的.
13.“小明和爸爸一起出门去散步,走到街心花园,小刚遇见了小红,两人玩了一会儿后,小明回家做作业了,爸爸看他们玩了一会儿后向远处的超市走去.”下面图
正确描述了小明的行为,图
正确描述了爸爸的行为.
14.某服装厂一、二车间产值情况统计如图.
(1)纵轴上每个单位长度表示
万元.
(2)一车间平均每季度产值
万元,二车间平均每季度产值
万元.
(3)第二季度一车间产值比二车间多
万元,二车间第三季度产值比第二季度多
万元.
15.明明和亮亮5次的跳远成绩如图,请根据统计图回答问题.
(1)明明和亮亮第一次跳远的成绩相差
米.
(2)他们第
次成绩相差最多.
(3)亮亮的成绩呈现
的变化趋势.
16.一个长方体容器(如图1)现在以每分钟25升的速度向这个容器注水,容器的底面有一块隔板(垂直于底面,不考虑厚度),将容器隔为A,B部分,B部分的底有一个洞,水按每分钟10升的速度往下漏.(如图2)表示从注水开始A部分水的高度变化情况,观察并思考回答下面的问题:
(1)隔板的高度是
分米.
(2)注水36分钟共漏出水
升.
(3)如果不让B部分的洞漏水,只要
分就能使水箱A部分的水位到达5分米.
三.判断题(共5小题)
17.折线统计图不能反映数量的多少.
.(判断对错)
18.折线统计图既可以表示数量的多少,又可以表示数量的增减变化情况.
.(判断对错)
19.任意两个单式折线统计图都可以合成一个复式折线统计图.
(判断对错)
20.根据统计表画折线统计图,要先根据数据描点,再顺次连线.
(判断对错)
21.折线统计图既可以表示数量的多少,也可以表示数量的增减情况.
.(判断对错)
四.应用题(共7小题)
22.振兴玩具厂1~5月的产值如图所示.
(1)这是一幅
统计图,横轴表示
,纵轴表示
,每格代表
.
(2)产值最高的是
月,5月的产值比4月的产值增加了
万元.
(3)该厂第一季度平均每月的产值是
.该厂的每月产值是呈
趋势.(填“上升”或“下降”)
(4)这种统计图的优点是
.
23.林场工作人员统计了两棵树木的生长情况,并制成了它们生长情况的统计图(如图)
①比较两棵树的生长情况,你发现了什么?
②当两树都停止生长后,两树高度相差多少米?
24.观察如图,完成问题.
(1)第1天
的成绩好,第2天
的成绩好.
(2)哪天两人成绩最接近?差多少下?
(3)如果从两人中选一人参加比赛,你会选准?并说明理由.
25.小丽驱车外出兜风,半途中突然有一只猫冲到车前,她用力刹车才没撞到它.小丽受惊后决定开车回家.以下的折线图是小丽行车的速度记录.
(1)小丽行车期间的最高车速是多少?
(2)小丽在什么时间为躲避那猫而踩刹车?
(3)由如图的数据,能否知道小丽回程的路线,是不是比她从家里出发到发生此意外事件的路线距离短?请解释你的答案.
26.如图是丽丽发热住院期间的体温记录情况统计图.
(1)这种统计图是
统计图.
(2)护士每
小时为丽丽量一次体温;丽丽体温最高是
摄氏度;丽丽4月8日12时的体温是
摄氏度.
(3)从体温看,丽丽的病情是恶化还是好转?为什么?
27.六年级(1)班从学校出发,乘大巴车去农场进行实践活动,之后返回学校(大巴车行驶速度不变),如图反映的是大巴车行驶路程与时间之间的关系.请同学们观察图象,进行数据分析,求大巴车离开学校多少小时时,大巴车与农场相距10km.
28.某市甲,乙两所学校学生参加课外活动情况统计图如下.
(1)哪﹣年两校参加课外活动的人数相差最多?相差多少人?
(2)两校参加课外活动的人数逐年增加,请你估计一下2016年甲校参加课外活动的有多少人,乙校参加课外活动的有多少人?
(3)甲校参加课外活动的人数在哪个时间段上升最多?
参考答案与试题解析
一.选择题(共8小题)
1.解:观察图可知,小明离的路程越来越多,走到5千米的地方路程不再增加,也就是到了学校
所以他从家到学校需要走5千米.
故选:A.
2.解:离家的距离是随着时间的变化而变化.
(1)先离家越来远,到了最远距离一半的时候想起把文件忘在家里了;
(2)然后返回家取文件,再去上班,由此越来越近直到为0;
(3)到家拿文件再去上班,离家越来越远,直到上班的地方;
(4)上班的时候即停留的那里,所以离家最远的时候也是一条线段;
(5)然后回家直到离家的距离为0.
符合妈妈上班、下班时间离家距离变化的是图A.
故选:A.
3.解:根据题意与分析可得:
表示乌龟赛跑的图象应该是一条一直上升的直线,且比兔子早到达终点;
表示兔子赛跑的图象应该是开始时是一条上升的直线,中途变为水平直线,然后又变为上升,且比乌龟晚到达终点;
所以,A图能反映这个故事情节.
故选:A.
4.解:淘气的这一过程可分成以下几段:
(1)从家出发到途中休息前,这一段时间里离家的距离越来越远;
(2)途中休息,这一段时间离家的距离不变;
(3)途中休息后到书城,这一段时间里离家的距离越来越远;
(4)在书城借书,这一段时间离家的距离不变;
(5)从书城回家,这一段时间里离家的距离越来越近.
只有选项C符合这一变化.
故选:C.
5.解:热水器内剩余水量为:
60×=30(升)
时间为:
10+5+15=30(分钟)
答:爸爸洗完澡水箱内的水量是30升,爸爸淘气都洗完澡所用的时间是30分钟.
故选:C.
6.解:首先排除A.图A所描述的走到音乐厅没有停留的时间.
再排除B.图B描述的不是从家出发.
图D.描述的走到音乐厅又返回家中,也不符合题意.
所以只有图C比较准确地反映了笑笑的行为.
故选:C.
7.解:在第30秒两架飞机的高度相差最大,相差27﹣8=19(米),
故选:C.
8.解:乙城市的月平均气温高于甲城市的月平均气温有3月和4月。
答:乙城市月平均气温高于甲城市的有2个月。
故选:A。
二.填空题(共8小题)
9.解:(1)2018年一月、四月的产量和2017年同期的产量相等.
(2)2018年三月的产量比2017年同期的产量增加最多.
(3)2018年一月的产量和二月的产量相等.
故答案为:一、四;三;一、二.
10.解:(1)根据折线统计图可知:国际长途电话前3分钟的花费为2.4元,
所以打2分钟为2.4元.
3分钟以上每分钟:
(4.4﹣2.4)÷(5﹣3)
=2÷2
=1(元)
答:打2分钟需要2.4元电话费,3分钟以上每分钟1元.
(2)(6﹣3)×1+2.4
=3+2.4
=5.4(元)
(10.4﹣2.4)÷1+3
=8+3
=11(分钟)
答:打6分钟需要5.4元,10.4元打了11分钟.
故答案为:2.4;1;5.4;11.
11.解:1)小明共行驶了
360千米.
(2)小明出发后,经过
6小时到达了目的地,途中休息了
1小时.
(3)360÷(6﹣1)
=360÷5
=75(千米/小时)
答:不算休息,小明平均每小时行驶
75千米.
故答案为:360;6;1;75.
12.解:(1)第一分店营业额更高。
(2)二月份至三月份第一分店营业额下降得最快。
(3)三月份两店的营业额比较接近,二月份相差较远。
(4)从三月份到四月份两店的营业额都是增长的。
故答案为:一;二、三;三、二;三、四。
13.解:小明用图来表示应是小明离家的距离逐渐变远,然后同小红玩时的距离固定,然后再离家变近;
爸爸用图来表示应是爸爸离家的距离逐渐变远,然后看小时同小红玩时的距离固定,然后再离家变远.
故选:C,B.
14.解:(1)纵轴上每个单位长度表示100万元.
(2)(250+360+510+340)÷4
=1460÷4
=365(万元)
(200+250+300+230)÷4
=980÷4
=245(万元)
答:一车间平均每季度产值是365万元,二车间平均每季度产值是245万元.
(3)360﹣250=110(万元)
300﹣250=50(万元)
答:第二季度一车间产值比二车间多110万元,二车间第三季度产值比第二季度多50万元.
故答案为:100;365、245;110、50,.
15.解:(1)2.8﹣2.7=0.1(米)
答:明明和亮亮第一次跳远的成绩相差0.1米.
(2)2.8﹣2.7=0.1(米)
3.0﹣2.8=0.2(米)
3.1﹣2.8=0.3(米)
3.2﹣2.5=0.7(米)
3.4﹣2.6=0.8(米)
0.8>0.7>0.3>0.2>0.1
答:他们第5次相差最多.
(3)亮亮的成绩第1次到第2次呈上升趋势,第3次有所下降,第4次、第5次呈上升趋势.
故答案为:0.1;5;上升.
16.解;(1)从统计图中可发现,当水达到2分米的时候,高度开始不变,因此,挡板的高度为2分米;
答:隔板的高度是2分米。
(2)注水36分钟共注水:
25×36=900(升)
水箱中的水的体积为:
(7.5+4.5)×10×5×1=600(升)
因此,注水36分钟共漏出水:
900﹣600=300(升);
答:注水36分钟共漏出水300升。
(3)要使水箱A部分的水位达到(5分)米,需注水600升,只要注水:
600÷25=24(分钟)
答:只要24分钟就能使水箱A部分的水位到达5分米。
故答案为:2;300;24。
三.判断题(共5小题)
17.解:根据折线统计图的特点可知:线统计图不但可以反映数量的多少,还能反映出数量的增减变化情况;
故答案为:×.
18.解:折线统计图既可以表示数量的多少,又可以表示数量的增减变化情况.
故答案为:√.
19.解:任何一幅复式折线统计图都能分成多幅单式折线统计图,但是任意两个单式折线统计图不一定合成一个复式折线统计图,所以本题说法错误;
故答案为:×.
20.解:根据统计表画折线统计图,要先根据数据描点,再顺次连线.
故答案为:√.
21.解:根据折线统计图的特点和作用,
可知折线统计图的特点是既可以表示数量的多少,也可以表示数量的增减变化趋势.
因此,折线统计图既可以表示数量的多少,也可以表示数量的增减情况.这种说法是正确的.
故答案为:√.
四.应用题(共7小题)
22.解:(1)这是一幅折线统计图,横轴表示月份,纵轴表示产值,每格代表5万元.
(2)40﹣35=5(万元)
答:产值最高的是5月份,5月份的产值比4月份的产值增加了5万元.
(3)(5+15+22)÷3
=42÷3
=14(万元)
答:该厂第一季度平均每月的产值是14万元,厂的每月产值是呈上升趋势.
(4)这种统计图的优点是:不仅能够反映数量的多少,而且能够反映数量增减变化的趋势.
故答案为:折线、月份、产值、5万元;5、5;14、上升.不仅能够反映数量的多少,而且能够反映数量增减变化的趋势.
23.解:①比较两棵树的生长情况,我发现:
甲乙两棵树开始的生长都很快,但在10年左右时,乙树停止生长,而甲树继续生长到16年左右才停止生长.
②9﹣7=2(米)
答:当两树都停止生长后,两树高度相差2米.
24.解:(1)因为153>152,155>154,所以第1天穆欣的成绩好,第2天回媛媛的成绩好.
(2)153﹣152=1(下)
155﹣154=1(下)
答:第1天和第2天两人成绩最接近,差1下.
(3)如果从两人中选一人参加比赛,会选回媛媛,因为回媛媛的成绩比穆欣的成绩好些,
故答案为:穆欣,回媛媛,回媛媛.
25.解:(
1
)小丽行车期间的最高车速是60千米/时.
(
2
)小丽在9:06为躲避那猫而踩刹车.
(
3
)答:由图中的数据,可以知道小丽回程的路线比她从家里出发到发生此意外事件的路线距离短.因为小丽从家里出发到发生意外事件时用了6分钟,回程时到发生意外事件时虽然也用了6分钟,虽然都用最高速度行了4分钟,但是回程时的最高速度只有36千米/时行了4分钟,而出发时用最高速度60千米/时却行了4分钟.用的时间虽然相同,但回程时的速度却很慢,所以回程时的路线短.
26.解:(1)这种统计图是折线统计图.
(2)护士每隔6小时为丽丽量一次体温,丽丽体温最高是39.5℃,丽丽4月8日12时的体温是37.5℃.
(3)从体温看,丽丽的病情是好转,因为她的体温逐渐接近正常体温.
故答案为:折线;6、39.5、37.5
27.解:(40﹣10)÷40
=30÷40
=0.75(小时)
答:大巴车离开学校0.75小时时,大巴车与农场相距10千米.
28.解:(1)2000﹣1250=750(人)
答:2015年两校参加课外活动的人数相差最多,相差750人.
(2)根据两校参加课外活动的人数逐年增加的人数,我估计2016年甲校参加课外活动的人数约有2800人;乙校参加课外活动的人数约有1500人.
(3)甲校参加课外活动的人数在2015年上升最多.
折线统计图与可能性》单元达标检测卷
一.选择题(共8小题)
1.如图是小明每天上学走的路程统计图,那么他从家到学校需要走( )千米.
A.5
B.2.5
C.10
2.妈妈早上去上班,走了一半的路程想起把文件忘在家里了,然后返回家取文件,再去上班,下班后直接回家,下面的
( )图反映出妈妈上班和下班离家距离的情况.
A.
B.
C.
D.
3.龟兔赛跑是我们非常熟悉的故事,故事大意是:乌龟和兔子赛跑,兔子开始就领先了乌龟很多,兔子不耐烦了,就在路边睡了一觉,而乌龟一直往目的地奔跑,最终乌龟获得了胜利.下面能反映这个故事情节的图是( )
A.
B.
C.
D.
4.淘气从家去书城,中途休息了几分钟,到书城买完书后直接回家.下面正确描述淘气这一过程的图象是( )
A.
B.
C.
D.
5.淘气家的热水器中有60L水,晚上,爸爸先洗了10min澡,用了一半的水.5min后,淘气也去洗澡,他洗了15min,把热水器中的水刚好用完了.下面能描述热水器中水的体积随时间变化的情况的是( )
A.
B.
C.
D.
6.笑笑从家出发去音乐厅,当走她了大约一半路程时,想起忘了带门票于是她回家取票,然后再去音乐厅,听完音乐后回家,下面( )幅图比较准确地反映了笑笑的行为.
A.
B.
C.
D.
7.如图是甲、乙两架航模飞机的飞行情况统计图,第( )秒两架飞机的高度相差最大.
A.20
B.25
C.30
D.35
8.如图是甲、乙两个城市今年上半年月平均气温统计图,从图中可以看出,乙城市月平均气温高于甲城市的有( )个月.
A.2
B.3
C.4
D.5
二.填空题(共8小题)
9.如图是食品厂2017年上半年和2018年上半年生产饮料的统计图.
(1)2018年
月的产量和2017年同期的产量相等.
(2)2018年
月的产量比2017年同期的增加最多.
(3)2018年
月的产量和
月的产量相等.
10.如图是打国际长途电话所需付的电话费与通话时间之间的关系图.
(1)打2分钟需要
元电话费,3分钟以上每分钟
元.
(2)打6分钟需要
元,10.4元打了
分钟.
11.下面是小明某天从家出发到山区的行车情况统计图.
小明某天外出行车情况统计图
(1)小明共行驶了
千米.
(2)小明出发后,经过
小时到达了目的地,途中休息了
小时.
(3)不算休息,小明平均每小时行驶
千米.
12.如图是某超市第一分店、第二分店上半年营业额情况统计图.
(1)第
分店营业额更高.
(2)
月份至
月份第一分店营业额下降得最快.
(3)
月份两个店营业额比较接近;
月份相差较远.
(4)
月份到
月份两店的营业额都是增长的.
13.“小明和爸爸一起出门去散步,走到街心花园,小刚遇见了小红,两人玩了一会儿后,小明回家做作业了,爸爸看他们玩了一会儿后向远处的超市走去.”下面图
正确描述了小明的行为,图
正确描述了爸爸的行为.
14.某服装厂一、二车间产值情况统计如图.
(1)纵轴上每个单位长度表示
万元.
(2)一车间平均每季度产值
万元,二车间平均每季度产值
万元.
(3)第二季度一车间产值比二车间多
万元,二车间第三季度产值比第二季度多
万元.
15.明明和亮亮5次的跳远成绩如图,请根据统计图回答问题.
(1)明明和亮亮第一次跳远的成绩相差
米.
(2)他们第
次成绩相差最多.
(3)亮亮的成绩呈现
的变化趋势.
16.一个长方体容器(如图1)现在以每分钟25升的速度向这个容器注水,容器的底面有一块隔板(垂直于底面,不考虑厚度),将容器隔为A,B部分,B部分的底有一个洞,水按每分钟10升的速度往下漏.(如图2)表示从注水开始A部分水的高度变化情况,观察并思考回答下面的问题:
(1)隔板的高度是
分米.
(2)注水36分钟共漏出水
升.
(3)如果不让B部分的洞漏水,只要
分就能使水箱A部分的水位到达5分米.
三.判断题(共5小题)
17.折线统计图不能反映数量的多少.
.(判断对错)
18.折线统计图既可以表示数量的多少,又可以表示数量的增减变化情况.
.(判断对错)
19.任意两个单式折线统计图都可以合成一个复式折线统计图.
(判断对错)
20.根据统计表画折线统计图,要先根据数据描点,再顺次连线.
(判断对错)
21.折线统计图既可以表示数量的多少,也可以表示数量的增减情况.
.(判断对错)
四.应用题(共7小题)
22.振兴玩具厂1~5月的产值如图所示.
(1)这是一幅
统计图,横轴表示
,纵轴表示
,每格代表
.
(2)产值最高的是
月,5月的产值比4月的产值增加了
万元.
(3)该厂第一季度平均每月的产值是
.该厂的每月产值是呈
趋势.(填“上升”或“下降”)
(4)这种统计图的优点是
.
23.林场工作人员统计了两棵树木的生长情况,并制成了它们生长情况的统计图(如图)
①比较两棵树的生长情况,你发现了什么?
②当两树都停止生长后,两树高度相差多少米?
24.观察如图,完成问题.
(1)第1天
的成绩好,第2天
的成绩好.
(2)哪天两人成绩最接近?差多少下?
(3)如果从两人中选一人参加比赛,你会选准?并说明理由.
25.小丽驱车外出兜风,半途中突然有一只猫冲到车前,她用力刹车才没撞到它.小丽受惊后决定开车回家.以下的折线图是小丽行车的速度记录.
(1)小丽行车期间的最高车速是多少?
(2)小丽在什么时间为躲避那猫而踩刹车?
(3)由如图的数据,能否知道小丽回程的路线,是不是比她从家里出发到发生此意外事件的路线距离短?请解释你的答案.
26.如图是丽丽发热住院期间的体温记录情况统计图.
(1)这种统计图是
统计图.
(2)护士每
小时为丽丽量一次体温;丽丽体温最高是
摄氏度;丽丽4月8日12时的体温是
摄氏度.
(3)从体温看,丽丽的病情是恶化还是好转?为什么?
27.六年级(1)班从学校出发,乘大巴车去农场进行实践活动,之后返回学校(大巴车行驶速度不变),如图反映的是大巴车行驶路程与时间之间的关系.请同学们观察图象,进行数据分析,求大巴车离开学校多少小时时,大巴车与农场相距10km.
28.某市甲,乙两所学校学生参加课外活动情况统计图如下.
(1)哪﹣年两校参加课外活动的人数相差最多?相差多少人?
(2)两校参加课外活动的人数逐年增加,请你估计一下2016年甲校参加课外活动的有多少人,乙校参加课外活动的有多少人?
(3)甲校参加课外活动的人数在哪个时间段上升最多?
参考答案与试题解析
一.选择题(共8小题)
1.解:观察图可知,小明离的路程越来越多,走到5千米的地方路程不再增加,也就是到了学校
所以他从家到学校需要走5千米.
故选:A.
2.解:离家的距离是随着时间的变化而变化.
(1)先离家越来远,到了最远距离一半的时候想起把文件忘在家里了;
(2)然后返回家取文件,再去上班,由此越来越近直到为0;
(3)到家拿文件再去上班,离家越来越远,直到上班的地方;
(4)上班的时候即停留的那里,所以离家最远的时候也是一条线段;
(5)然后回家直到离家的距离为0.
符合妈妈上班、下班时间离家距离变化的是图A.
故选:A.
3.解:根据题意与分析可得:
表示乌龟赛跑的图象应该是一条一直上升的直线,且比兔子早到达终点;
表示兔子赛跑的图象应该是开始时是一条上升的直线,中途变为水平直线,然后又变为上升,且比乌龟晚到达终点;
所以,A图能反映这个故事情节.
故选:A.
4.解:淘气的这一过程可分成以下几段:
(1)从家出发到途中休息前,这一段时间里离家的距离越来越远;
(2)途中休息,这一段时间离家的距离不变;
(3)途中休息后到书城,这一段时间里离家的距离越来越远;
(4)在书城借书,这一段时间离家的距离不变;
(5)从书城回家,这一段时间里离家的距离越来越近.
只有选项C符合这一变化.
故选:C.
5.解:热水器内剩余水量为:
60×=30(升)
时间为:
10+5+15=30(分钟)
答:爸爸洗完澡水箱内的水量是30升,爸爸淘气都洗完澡所用的时间是30分钟.
故选:C.
6.解:首先排除A.图A所描述的走到音乐厅没有停留的时间.
再排除B.图B描述的不是从家出发.
图D.描述的走到音乐厅又返回家中,也不符合题意.
所以只有图C比较准确地反映了笑笑的行为.
故选:C.
7.解:在第30秒两架飞机的高度相差最大,相差27﹣8=19(米),
故选:C.
8.解:乙城市的月平均气温高于甲城市的月平均气温有3月和4月。
答:乙城市月平均气温高于甲城市的有2个月。
故选:A。
二.填空题(共8小题)
9.解:(1)2018年一月、四月的产量和2017年同期的产量相等.
(2)2018年三月的产量比2017年同期的产量增加最多.
(3)2018年一月的产量和二月的产量相等.
故答案为:一、四;三;一、二.
10.解:(1)根据折线统计图可知:国际长途电话前3分钟的花费为2.4元,
所以打2分钟为2.4元.
3分钟以上每分钟:
(4.4﹣2.4)÷(5﹣3)
=2÷2
=1(元)
答:打2分钟需要2.4元电话费,3分钟以上每分钟1元.
(2)(6﹣3)×1+2.4
=3+2.4
=5.4(元)
(10.4﹣2.4)÷1+3
=8+3
=11(分钟)
答:打6分钟需要5.4元,10.4元打了11分钟.
故答案为:2.4;1;5.4;11.
11.解:1)小明共行驶了
360千米.
(2)小明出发后,经过
6小时到达了目的地,途中休息了
1小时.
(3)360÷(6﹣1)
=360÷5
=75(千米/小时)
答:不算休息,小明平均每小时行驶
75千米.
故答案为:360;6;1;75.
12.解:(1)第一分店营业额更高。
(2)二月份至三月份第一分店营业额下降得最快。
(3)三月份两店的营业额比较接近,二月份相差较远。
(4)从三月份到四月份两店的营业额都是增长的。
故答案为:一;二、三;三、二;三、四。
13.解:小明用图来表示应是小明离家的距离逐渐变远,然后同小红玩时的距离固定,然后再离家变近;
爸爸用图来表示应是爸爸离家的距离逐渐变远,然后看小时同小红玩时的距离固定,然后再离家变远.
故选:C,B.
14.解:(1)纵轴上每个单位长度表示100万元.
(2)(250+360+510+340)÷4
=1460÷4
=365(万元)
(200+250+300+230)÷4
=980÷4
=245(万元)
答:一车间平均每季度产值是365万元,二车间平均每季度产值是245万元.
(3)360﹣250=110(万元)
300﹣250=50(万元)
答:第二季度一车间产值比二车间多110万元,二车间第三季度产值比第二季度多50万元.
故答案为:100;365、245;110、50,.
15.解:(1)2.8﹣2.7=0.1(米)
答:明明和亮亮第一次跳远的成绩相差0.1米.
(2)2.8﹣2.7=0.1(米)
3.0﹣2.8=0.2(米)
3.1﹣2.8=0.3(米)
3.2﹣2.5=0.7(米)
3.4﹣2.6=0.8(米)
0.8>0.7>0.3>0.2>0.1
答:他们第5次相差最多.
(3)亮亮的成绩第1次到第2次呈上升趋势,第3次有所下降,第4次、第5次呈上升趋势.
故答案为:0.1;5;上升.
16.解;(1)从统计图中可发现,当水达到2分米的时候,高度开始不变,因此,挡板的高度为2分米;
答:隔板的高度是2分米。
(2)注水36分钟共注水:
25×36=900(升)
水箱中的水的体积为:
(7.5+4.5)×10×5×1=600(升)
因此,注水36分钟共漏出水:
900﹣600=300(升);
答:注水36分钟共漏出水300升。
(3)要使水箱A部分的水位达到(5分)米,需注水600升,只要注水:
600÷25=24(分钟)
答:只要24分钟就能使水箱A部分的水位到达5分米。
故答案为:2;300;24。
三.判断题(共5小题)
17.解:根据折线统计图的特点可知:线统计图不但可以反映数量的多少,还能反映出数量的增减变化情况;
故答案为:×.
18.解:折线统计图既可以表示数量的多少,又可以表示数量的增减变化情况.
故答案为:√.
19.解:任何一幅复式折线统计图都能分成多幅单式折线统计图,但是任意两个单式折线统计图不一定合成一个复式折线统计图,所以本题说法错误;
故答案为:×.
20.解:根据统计表画折线统计图,要先根据数据描点,再顺次连线.
故答案为:√.
21.解:根据折线统计图的特点和作用,
可知折线统计图的特点是既可以表示数量的多少,也可以表示数量的增减变化趋势.
因此,折线统计图既可以表示数量的多少,也可以表示数量的增减情况.这种说法是正确的.
故答案为:√.
四.应用题(共7小题)
22.解:(1)这是一幅折线统计图,横轴表示月份,纵轴表示产值,每格代表5万元.
(2)40﹣35=5(万元)
答:产值最高的是5月份,5月份的产值比4月份的产值增加了5万元.
(3)(5+15+22)÷3
=42÷3
=14(万元)
答:该厂第一季度平均每月的产值是14万元,厂的每月产值是呈上升趋势.
(4)这种统计图的优点是:不仅能够反映数量的多少,而且能够反映数量增减变化的趋势.
故答案为:折线、月份、产值、5万元;5、5;14、上升.不仅能够反映数量的多少,而且能够反映数量增减变化的趋势.
23.解:①比较两棵树的生长情况,我发现:
甲乙两棵树开始的生长都很快,但在10年左右时,乙树停止生长,而甲树继续生长到16年左右才停止生长.
②9﹣7=2(米)
答:当两树都停止生长后,两树高度相差2米.
24.解:(1)因为153>152,155>154,所以第1天穆欣的成绩好,第2天回媛媛的成绩好.
(2)153﹣152=1(下)
155﹣154=1(下)
答:第1天和第2天两人成绩最接近,差1下.
(3)如果从两人中选一人参加比赛,会选回媛媛,因为回媛媛的成绩比穆欣的成绩好些,
故答案为:穆欣,回媛媛,回媛媛.
25.解:(
1
)小丽行车期间的最高车速是60千米/时.
(
2
)小丽在9:06为躲避那猫而踩刹车.
(
3
)答:由图中的数据,可以知道小丽回程的路线比她从家里出发到发生此意外事件的路线距离短.因为小丽从家里出发到发生意外事件时用了6分钟,回程时到发生意外事件时虽然也用了6分钟,虽然都用最高速度行了4分钟,但是回程时的最高速度只有36千米/时行了4分钟,而出发时用最高速度60千米/时却行了4分钟.用的时间虽然相同,但回程时的速度却很慢,所以回程时的路线短.
26.解:(1)这种统计图是折线统计图.
(2)护士每隔6小时为丽丽量一次体温,丽丽体温最高是39.5℃,丽丽4月8日12时的体温是37.5℃.
(3)从体温看,丽丽的病情是好转,因为她的体温逐渐接近正常体温.
故答案为:折线;6、39.5、37.5
27.解:(40﹣10)÷40
=30÷40
=0.75(小时)
答:大巴车离开学校0.75小时时,大巴车与农场相距10千米.
28.解:(1)2000﹣1250=750(人)
答:2015年两校参加课外活动的人数相差最多,相差750人.
(2)根据两校参加课外活动的人数逐年增加的人数,我估计2016年甲校参加课外活动的人数约有2800人;乙校参加课外活动的人数约有1500人.
(3)甲校参加课外活动的人数在2015年上升最多.
