人教版七年级上册数学3.3 解一元一次方程(二)同步练习(Word版 含解析)
文档属性
| 名称 | 人教版七年级上册数学3.3 解一元一次方程(二)同步练习(Word版 含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 42.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-19 00:00:00 | ||
图片预览



文档简介
解一元一次方程2
一、选择题
1.某班级劳动时,将全班同学分成x个小组,若每小组11人,则余下1人;若每小组12人,则有一组少4人.按下列哪个选项重新分组,能使每组人数相同?( )
A.
3组
B.
5组
C.
6组
D.
7组
2.解方程时,去分母,去括号后,正确结果是(
).
A.4x+1-10x+1=1
B.4x+2-10x-1=1
C.4x+2-10x-1=6
D以上都不对
3.几个人共同种一批树苗,如果每人种5棵,则剩下3棵树苗未种;如果每人种6棵,则缺4棵树苗.若设参与种树的人数为x人,则下面所列方程中正确的是( )
A.
5x+3=6x-4
B.
5x+3=6x+4
C.
5x-3=6x-4
D.
5x-3=6x+4
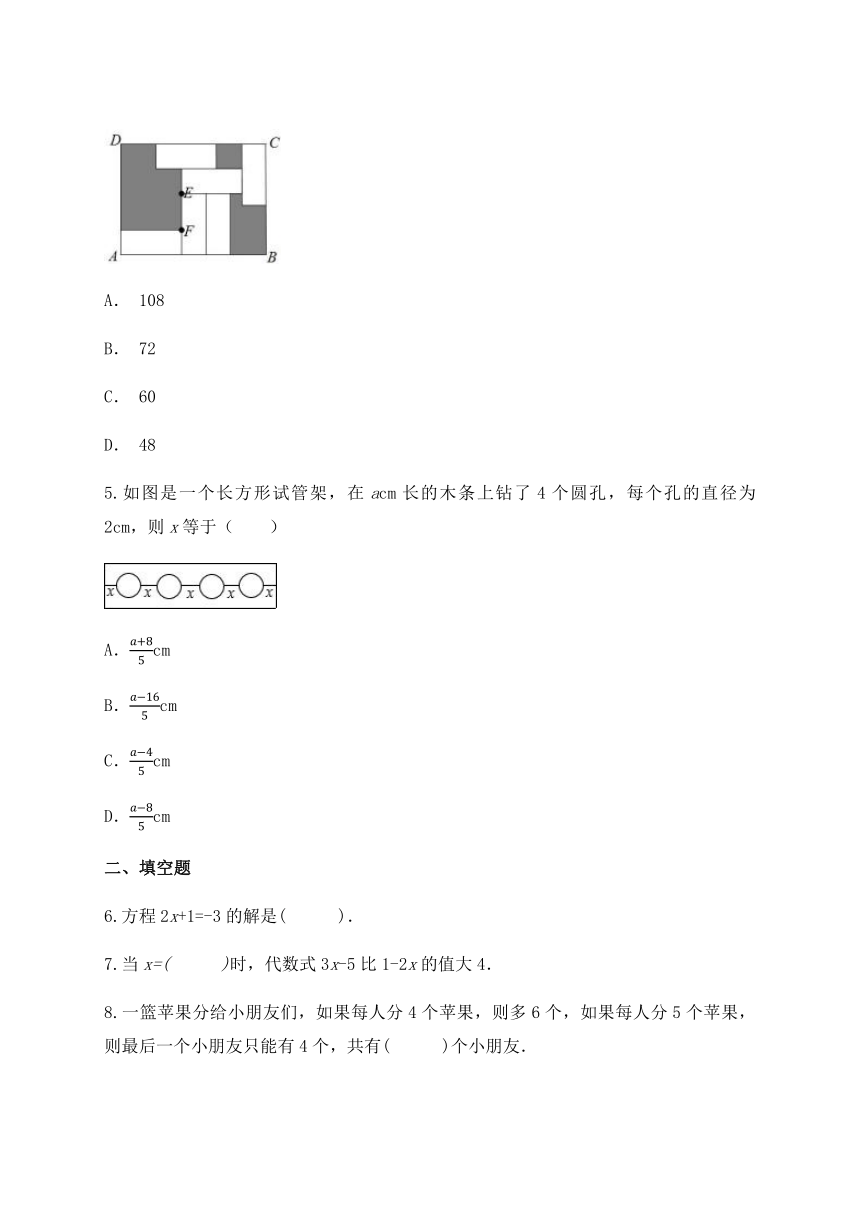
4.如图,长方形ABCD中有6个形状、大小相同的小长方形,且EF=3,CD=12,则图中阴影部分的面积为( )
A.
108
B.
72
C.
60
D.
48
5.如图是一个长方形试管架,在acm长的木条上钻了4个圆孔,每个孔的直径为2cm,则x等于( )
A.cm
B.cm
C.cm
D.cm
二、填空题
6.方程2x+1=-3的解是(
).
7.当x=(
)时,代数式3x-5比1-2x的值大4.
8.一篮苹果分给小朋友们,如果每人分4个苹果,则多6个,如果每人分5个苹果,则最后一个小朋友只能有4个,共有(
)个小朋友.
9/如果5(x+2)=2a+3与的解相同,那么a的值是________.
三、解答题
10.长方形纸片的长是15cm,长宽上各剪去两个宽为3cm的长条,剩下的面积是原面积的.求原面积.
11.如图,几块大小不等的正方形纸片无重叠地铺满了一块长方形.已知正方形纸片A的边长为7,求最小的正方形纸片的边长.
12.已知一个长方形的周长为60cm.
(1)若它的长比宽多6cm,这个长方形的宽是多少cm?
(2)若它的长与宽的比是2:1,这个长方形的长是多少cm?
13.某工厂计划26小时生产一批零件,后因每小时多生产5件,用24小时,不但完成了任务,而且还比原计划多生产了60件,问原计划生产多少零件?
14、解方程:.
答案解析
1.【答案】D
【解析】根据全班同学人数不变以及“将全班同学分成x个小组,若每小组11人,则余下1人;若每小组12人,则有一组少4人”列出方程,求解即可.
解:设将全班同学分成x个小组,根据题意得
11x+1=12x-4,
解得x=5,
所以全班同学共有:11x+1=11×5+1=56人,
56=7×8,
则将全班同学分成7个小组,能使每组人数相同.
故选D.
2.【答案】C
3.【答案】A
【解析】设有x人参加种树,
5x+3=6x-4.
故选A.
4.【答案】D
【解析】设每小长方形的宽为x,则每小长方形的长为x+3,
根据一个小长方形的宽+2个小长方形的长=CD,
列出方程,求出x的值,
再根据长方形的面积公式用最大的长方形减去6个最小的小长方形的面积,
得出阴影部分的面积.
解:设每小长方形的宽为x,则每小长方形的长为x+3,根据题意得:
2(x+3)+x=12,
解得:x=2,
则每小长方形的长为2+3=5,
则AD=2+2+5=9,
阴影部分的面积为9×12-2×5×6=48;
故选D.
5.【答案】D
【解析】根据条件就可以得出5x+4×2=a,然后求出该方程的解即可.
解:由题意,得
5x+4×2=a,
解得:x=.
故选D.
6/【答案】x=-2
【解析】移项合并得:2x=-4,
解得:x=-2.
故答案为:x=-2.
7.【答案】=2
【解析】根据代数式3x-5比1-2x的值大4,可以列方程:(3x-5)-(1-2x)=4,解方程即可求得x的值.
解:根据题意得:(3x-5)-(1-2x)=4,
去括号,得:3x-5-1+2x=4,
移项,合并同类项得,5x=10,
解得:x=2.
故答案是:=2.
8.【答案】7
【解析】设共有x个小朋友,则苹果有(4x+6)个,则
(4x+6)-5(x-1)=4,
整理,得
-x+11=4,
解得x=7.
故答案是:7.
9、
10.【答案】解:设长方形纸片的宽是xcm,原面积是15xcm2,
长宽上各剪去两个宽为3cm的长条,剩下的面积是12?(x-3)cm2,
∵15x×=9x,
∴9x=12?(x-3),
解可得x=12,
∴原面积是180cm2.
【解析】由题意可知剩下的面积是原面积的,由此列方程可求解.
11.【答案】解:设最小的正方形纸片的边长为x.
则B,C,D,E,F,G,H的边长依次为x+7,2x+7,3x+7,7x+7,4x,11x+7,x+14,
根据H的边长列方程:11x+7-(7-4x)=14+x,
解得:x=1.
答:最小的正方形纸片的边长为1.
或根据长方形的对边相等,列方程:
2x+7+x+7+x+14=7x+7+11x+7,
解得:x=1.
答:最小的正方形纸片的边长为1.
【解析】可从中间最小的正方形的边长入手思考,表示出其余正方形的边长,根据正方形的边长相等列式求解即可.
12.【答案】解:(1)设长方形的宽为xcm,则长为(x+6)cm,由题意得
2[x+(x+6)]=60,
解得:x=12.
答:这个长方形的宽是12cm;
(2)设长方形的宽为acm,则长为2acm,由题意得
2(2a+a)=60,
解得:a=10,
2a=20.
答:这个长方形的长是20cm.
【解析】(1)设长方形的宽为xcm,则长为(x+6)cm,根据长方形的周长为60cm列出方程解答即可;
(2)设长方形的宽为acm,则长为2acm,根据长方形的周长为60cm列出方程解答即可.
13.【答案】解:设原计划每小时生产x件零件,由题意得:
26x+60=24(x+5),
解得:x=30,
所以原计划生产零件件数为:26x=780,
答:原计划生产780件零件.
【解析】设原计划每小时生产x件零件,则实际生产(26x+60)件.题目中的相等关系是:实际24小时生产的件数=计划26小时生产的件数+60.根据相等关系就可以列出方程求解.
14、解:去分母,得:2(4-6x)-6=3(2x+1).
去括号,得:8-12x-6=6x+3.
移项,合并同类项,得:-18x=1.
系数化为1,得:.
一、选择题
1.某班级劳动时,将全班同学分成x个小组,若每小组11人,则余下1人;若每小组12人,则有一组少4人.按下列哪个选项重新分组,能使每组人数相同?( )
A.
3组
B.
5组
C.
6组
D.
7组
2.解方程时,去分母,去括号后,正确结果是(
).
A.4x+1-10x+1=1
B.4x+2-10x-1=1
C.4x+2-10x-1=6
D以上都不对
3.几个人共同种一批树苗,如果每人种5棵,则剩下3棵树苗未种;如果每人种6棵,则缺4棵树苗.若设参与种树的人数为x人,则下面所列方程中正确的是( )
A.
5x+3=6x-4
B.
5x+3=6x+4
C.
5x-3=6x-4
D.
5x-3=6x+4
4.如图,长方形ABCD中有6个形状、大小相同的小长方形,且EF=3,CD=12,则图中阴影部分的面积为( )
A.
108
B.
72
C.
60
D.
48
5.如图是一个长方形试管架,在acm长的木条上钻了4个圆孔,每个孔的直径为2cm,则x等于( )
A.cm
B.cm
C.cm
D.cm
二、填空题
6.方程2x+1=-3的解是(
).
7.当x=(
)时,代数式3x-5比1-2x的值大4.
8.一篮苹果分给小朋友们,如果每人分4个苹果,则多6个,如果每人分5个苹果,则最后一个小朋友只能有4个,共有(
)个小朋友.
9/如果5(x+2)=2a+3与的解相同,那么a的值是________.
三、解答题
10.长方形纸片的长是15cm,长宽上各剪去两个宽为3cm的长条,剩下的面积是原面积的.求原面积.
11.如图,几块大小不等的正方形纸片无重叠地铺满了一块长方形.已知正方形纸片A的边长为7,求最小的正方形纸片的边长.
12.已知一个长方形的周长为60cm.
(1)若它的长比宽多6cm,这个长方形的宽是多少cm?
(2)若它的长与宽的比是2:1,这个长方形的长是多少cm?
13.某工厂计划26小时生产一批零件,后因每小时多生产5件,用24小时,不但完成了任务,而且还比原计划多生产了60件,问原计划生产多少零件?
14、解方程:.
答案解析
1.【答案】D
【解析】根据全班同学人数不变以及“将全班同学分成x个小组,若每小组11人,则余下1人;若每小组12人,则有一组少4人”列出方程,求解即可.
解:设将全班同学分成x个小组,根据题意得
11x+1=12x-4,
解得x=5,
所以全班同学共有:11x+1=11×5+1=56人,
56=7×8,
则将全班同学分成7个小组,能使每组人数相同.
故选D.
2.【答案】C
3.【答案】A
【解析】设有x人参加种树,
5x+3=6x-4.
故选A.
4.【答案】D
【解析】设每小长方形的宽为x,则每小长方形的长为x+3,
根据一个小长方形的宽+2个小长方形的长=CD,
列出方程,求出x的值,
再根据长方形的面积公式用最大的长方形减去6个最小的小长方形的面积,
得出阴影部分的面积.
解:设每小长方形的宽为x,则每小长方形的长为x+3,根据题意得:
2(x+3)+x=12,
解得:x=2,
则每小长方形的长为2+3=5,
则AD=2+2+5=9,
阴影部分的面积为9×12-2×5×6=48;
故选D.
5.【答案】D
【解析】根据条件就可以得出5x+4×2=a,然后求出该方程的解即可.
解:由题意,得
5x+4×2=a,
解得:x=.
故选D.
6/【答案】x=-2
【解析】移项合并得:2x=-4,
解得:x=-2.
故答案为:x=-2.
7.【答案】=2
【解析】根据代数式3x-5比1-2x的值大4,可以列方程:(3x-5)-(1-2x)=4,解方程即可求得x的值.
解:根据题意得:(3x-5)-(1-2x)=4,
去括号,得:3x-5-1+2x=4,
移项,合并同类项得,5x=10,
解得:x=2.
故答案是:=2.
8.【答案】7
【解析】设共有x个小朋友,则苹果有(4x+6)个,则
(4x+6)-5(x-1)=4,
整理,得
-x+11=4,
解得x=7.
故答案是:7.
9、
10.【答案】解:设长方形纸片的宽是xcm,原面积是15xcm2,
长宽上各剪去两个宽为3cm的长条,剩下的面积是12?(x-3)cm2,
∵15x×=9x,
∴9x=12?(x-3),
解可得x=12,
∴原面积是180cm2.
【解析】由题意可知剩下的面积是原面积的,由此列方程可求解.
11.【答案】解:设最小的正方形纸片的边长为x.
则B,C,D,E,F,G,H的边长依次为x+7,2x+7,3x+7,7x+7,4x,11x+7,x+14,
根据H的边长列方程:11x+7-(7-4x)=14+x,
解得:x=1.
答:最小的正方形纸片的边长为1.
或根据长方形的对边相等,列方程:
2x+7+x+7+x+14=7x+7+11x+7,
解得:x=1.
答:最小的正方形纸片的边长为1.
【解析】可从中间最小的正方形的边长入手思考,表示出其余正方形的边长,根据正方形的边长相等列式求解即可.
12.【答案】解:(1)设长方形的宽为xcm,则长为(x+6)cm,由题意得
2[x+(x+6)]=60,
解得:x=12.
答:这个长方形的宽是12cm;
(2)设长方形的宽为acm,则长为2acm,由题意得
2(2a+a)=60,
解得:a=10,
2a=20.
答:这个长方形的长是20cm.
【解析】(1)设长方形的宽为xcm,则长为(x+6)cm,根据长方形的周长为60cm列出方程解答即可;
(2)设长方形的宽为acm,则长为2acm,根据长方形的周长为60cm列出方程解答即可.
13.【答案】解:设原计划每小时生产x件零件,由题意得:
26x+60=24(x+5),
解得:x=30,
所以原计划生产零件件数为:26x=780,
答:原计划生产780件零件.
【解析】设原计划每小时生产x件零件,则实际生产(26x+60)件.题目中的相等关系是:实际24小时生产的件数=计划26小时生产的件数+60.根据相等关系就可以列出方程求解.
14、解:去分母,得:2(4-6x)-6=3(2x+1).
去括号,得:8-12x-6=6x+3.
移项,合并同类项,得:-18x=1.
系数化为1,得:.
