人教版数学七年级下册 8.3 实际问题与二元一次方程组 课件(35张)
文档属性
| 名称 | 人教版数学七年级下册 8.3 实际问题与二元一次方程组 课件(35张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-19 00:00:00 | ||
图片预览











文档简介
第八章 二元一次方程组
8.3 实际问题与二元一次方程组
1.能够根据具体的数量关系,列出二元一次方程
组解决简单的实际问题;(重点)
2.学会利用二元一次方程组解决几何、行程问题.
(重点、难点)
学习目标
新课讲解
合作与交流
问题1 题中有哪些未知量,你如何设未知数?
未知量:每头大牛1天需用的饲料;
每头小牛1天需用的饲料.
问题2 题中有哪些等量关系?
(1)30只大牛和15只小牛一天需用饲料为675kg;
(2)(30+12)只大牛和(15+5)只小牛一天需用饲料为940kg.
设未知数:设每头大牛和每头小牛平均1天各需用饲料为xkg和ykg,
新课讲解
解:设每头大牛和小牛平均1天各需用饲料为xkg和ykg,
根据等量关系,列方程组:
答:每头大牛和每头小牛1天各需用饲料为20kg和5kg,饲养员李大叔估计每天大牛需用饲料18到20千克,每头小牛一天需用7到8千克与计算有一定的出入.
+ = 675,
+ = 940.
30x
15y
42x
20y
解方程组: x= ,
y= .
20
5
新课讲解
剧情发展:随着养牛场规模逐渐扩大,李大叔需聘请饲养员协助管理现有的42头大牛和20头小牛,已知甲种饲养员每人可负责8头大牛和4头小牛,乙种饲养员每人可负责5头大牛和2头小牛,请问李大叔应聘请甲、乙两种饲养员各多少人?
解:设李大叔应聘请甲种饲养员x人,乙种饲养员y人,则:
+ = 42,
+ = 20.
8x
5y
4x
2y
解得:
x =4
y = 2
答:李大叔应聘请甲种饲养员4人,乙种饲养员2人.
新课讲解
典例精析
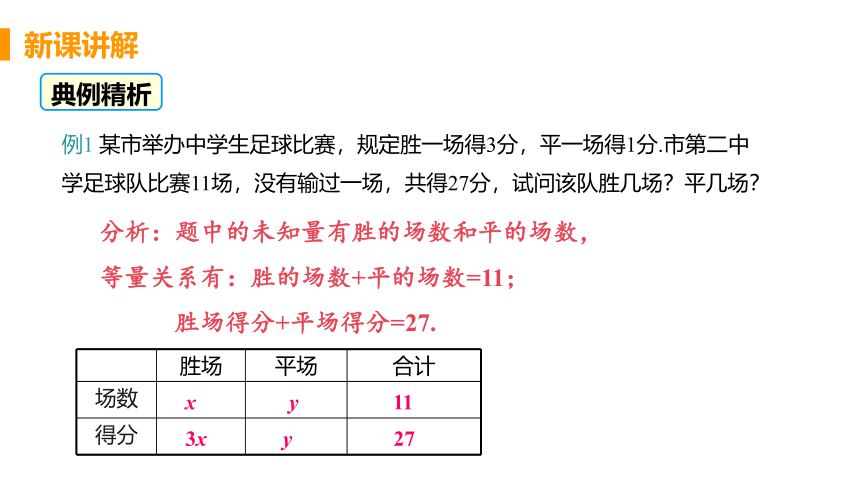
例1 某市举办中学生足球比赛,规定胜一场得3分,平一场得1分.市第二中学足球队比赛11场,没有输过一场,共得27分,试问该队胜几场?平几场?
分析:题中的未知量有胜的场数和平的场数,等量关系有:胜的场数+平的场数=11;
胜场得分+平场得分=27.
胜场
平场
合计
场数
得分
x
3x
y
y
11
27
新课讲解
解:设市第二中学足球队胜x场,平y场.依题意可得
8
y
3x
y
3
答:该市第二中学足球队胜8场,平3场.
x
通过上述两题,总结
用二元一次方程组解
决实际问题的步骤
新课讲解
解题小结:用二元一次方程组解决实际问题的步骤:
(1)审题:弄清题意和题目中的_________;
(2)设元:用___________表示题目中的未知数;
(3)列方程组:根据___个等量关系列出方程组;
(4)解方程组:利用____________或___________解
出未知数的值;
(5)检验并答:检验所求的解是否符合实际意义,
然后作答.
总结归纳
数量关系
字母
2
代入消元法
加减消元法
新课讲解
练一练1:某城市规定:出租车起步价所包含的路程为0~3km,超过3km的部分按每千米另收费.
甲说:“我乘这种出租车走了11km,付了17元.”
乙说:“我乘这种出租车走了23km,付了35元.”
请你算一算:出租车的起步价是多少元?超过3km后,每千米的车费是多少元?
分析 本问题涉及的等量关系有:
总车费=0~3km的车费(起步价)+超过3km的车费.
新课讲解
解 设出租车的起步价是x元,超过3km后每千米收费y元.
根据等量关系,得
解这个方程组,得
答:这种出租车的起步价是5元,超过3km后每千米收费1.5元.
起步价
超过3km后的费用
合计费用
甲
乙
x
x
(11-3)y
(23-3)y
17
35
新课讲解
练一练2:今有牛五、羊二,直金十两.牛二、羊五,直金八两.牛、羊各直金几何?
牛五、羊二
牛二、羊五
新课讲解
5头牛、2只羊共价值10两“金”;2头牛、5只羊共价值8两“金”.问每头牛、每只羊各价值多少“金”?
题目大意
解:设每头牛值“金”x两,每只羊值“金”y两,
由题意,得
5x+2y=10,
2x+5y=8.
解得
x=
y=
{
答:羊值“金” 两,牛值“金” 两.
新课讲解
知识点2 列方程组解决几何问题
据统计资料,甲、乙两种作物的单位面积产量的比是1:2.现要把一块长200m、宽100m的长方形土地,分为两块小长方形土地,分别种植这两种作物.怎样划分这块土地,使甲、乙两种作物的总产量的比是3:4?
请提取数学信息
新课讲解
转换成数学语言:
A
D
C
B
已知:长方形ABCD, AB=CD=200m,AD=BC=100m,长方形ABCD分割为两个小长方形,长方形1和长方形2分别种甲、乙作物,甲、乙单位面积产量的比是1:2.
目标:甲、乙两种作物的总产量的比是3:4
新课讲解
这里研究的实际上是 什么 问题.
分
析
把一个长方形分成两个小长方形有哪些分割方式?
01
竖着画,把长分成两段,则宽不变
02
横着画,把宽分成两段,则长不变
长方形的面积分割
我们可以画出示意图来帮助分析
试着画一画
新课讲解
01
竖着画,把长分成两段,则宽不变
A
D
C
F
B
E
1.大长方形的长=200m
2.甲、乙两种作物总产量比=3:4
等量关系式有几个?
分
析
新课讲解
01
竖着画,把长分成两段,则宽不变
A
D
C
F
B
E
1.大长方形的长=200m
2.甲、乙两种作物总产量比=3:4
分
析
设AE=xm,BE=ym.
先求出两种作物的面积
SAEFD=100x
SEFCB=100y
再写出两种作物的总产量
甲:100x×1
乙:100y×2
则列方程为
100x:200y=3:4
总产量=
?
1 : 2
x
y
200m
100
如何设未知数呢?
则列方程为
x+y=200
单位面积产量×面积
新课讲解
01
竖着画,把长分成两段,则宽不变
A
D
C
F
B
E
根据题意列方程组为
100x:200y=3:4
x
y
200m
100m
解
答
x+y=200
解得
x=120
y=80
你觉得该如何答题比较完整呢?
甲种作物
乙种作物
解:
过点E作EF⊥AB,
交CD于点F.
设AE=xm,BE=ym.
答:将这块土地分为长120m,宽100m和长100m,宽80m的
两个小长方形分别种植甲、乙两种作物.
新课讲解
02
横着画,把宽分成两段,则长不变
A
D
C
B
E
x
y
F
x+y=100
乙种作物
甲种作物
解:过点E作EF⊥AD,交BC于点F.
设DE=xm,AE=ym.
200x:400y=3:4
200y
200x
x=60
y=40
解得
解
答
根据题意列方程组为
200m
100m
答:将这块土地分为长200m,宽60m和长200m,宽40m的
两个小长方形分别种植甲、乙两种作物.
新课讲解
练一练: 如图,8块相同的小长方形地砖拼成一个大长方形,每块小长方形地砖的长和宽分别是多少?(单位:cm)
60
x+y=60
x=3y
解:设小长方形地砖的长为x, 宽为y,
由题意,得
解此方程组得:
x =45,
y=15.
答:小长方形地砖的长为45cm, 宽为15cm.
新课讲解
知识点3 列方程组解决行程问题
小华从家里到学校的路是一段平路和一段下坡路. 假设他始终保持平路每分钟走60m,下坡路每分钟走80m,上坡路每分钟走40m,则他从家里到学校需10min,从学校到家里需15min.问小华家离学校多远?
新课讲解
分析:小华到学校的路分成两段,一段为平路,
一段为下坡路.
平路:60 m/min
下坡路:80 m/min
上坡路:40 m/min
走平路的时间+走下坡路的时间=________,
走上坡路的时间+走平路的时间= _______.
路程=平均速度×时间
10
15
新课讲解
方法一(直接设元法)
平路时间
坡路时间
总时间
上学
放学
解:设小华家到学校平路长x m,下坡路长y m.
根据题意,可列方程组:
解方程组,得
所以,小明家到学校的距离为700m.
新课讲解
方法二(间接设元法)
平路
距离
坡路距离
上学
放学
解:设小华下坡路所花时间为xmin,上坡路所花时间为ymin.
根据题意,可列方程组:
解方程组,得
所以,小明家到学校的距离为700m.
故 平路距离:60×(10-5)=300(m)
坡路距离:80×5=400(m)
新课讲解
例2 甲、乙两人相距4km,以各自的速度同时出发.如果同向而行,甲2h追上乙;如果相向而行,两人0.5h后相遇.试问两人的速度各是多少?
典例精析
分析:对于行程问题,一般可以借助示意图表示题中的数量关系,可以更加直观的找到相等关系.
新课讲解
(1) 同时出发,同向而行
甲出发点
乙出发点
4km
甲追上乙
乙2h行程
甲2h行程
甲2h行程=4km+乙2h行程
(2) 同时出发,相向而行
甲出发点
乙出发点
4km
相遇地
甲0.5h
行程
乙0.5h
行程
甲0.5h行程+乙0.5h行程=4km
新课讲解
解:设甲、乙的速度分别为xkm/h,ykm/h.
根据题意,得
解方程组,得
答:甲的速度为5km/h,乙的速度为3km/h.
新课讲解
练一练:我国的长江由西至东奔腾不息,其中九江至南京约有450千米的路程,某船从九江出发9小时就能到达南京;返回时则用多了1小时.求此船在静水中的速度以及长江水的平均流速.
解:设轮船在静水中的速度为x千米/时,长江水的平均流速为y千米/时.
答:轮船在静水中的速度为47.5千米/时,长江水的平均流速为2.5千米/时.
课堂小结
二元一次方程组的应用
应用
步骤
简单实际问题
行程问题
路程=平均速度×时间
审题:弄清题意和题目中的
设元:用_____表示题目中的未知数
列方程组:根据__个等量关系列出方程组
解方程组
检验作答
数量关系
字母
2
代入法;
加减法.
几何问题
当堂小练
1.计划若干节车皮装运一批货物.如果每节装15.5吨,则有4吨装不下,如果每节装16.5吨,则还可多装8吨.问有多少节车皮?多少吨货物?
解:设有x节车皮,y吨货物,根据题意列出方程组得
y=15.5x+4,
y=16.5x-8.
(以下部分由同学们完成)
当堂小练
2.某班有40名同学看演出,购买甲、乙两种票共用去370元,其中甲种票每张10元,乙种票每张8元.请问甲种和乙种票各多少张?
解得
答:甲种票25张,乙种票15张.
当堂小练
3.课本中介绍我国古代数学名著《孙子算经》上有这样的一道题:今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各多少只?
解得
答:鸡有23只,兔有12只.
当堂小练
4.有甲、乙两数,甲数的3倍与乙数的2倍之和等于47,甲数的5倍比乙数的6倍小1,这两个数分别是多少?
解得
答:甲数为10,乙数为 .
拓展与延伸
隔壁听到人分银,
不知人数不知银.
每人五两多六两,
每人六两少五两.
多少人数多少银?
解:设有x个人,y两银,
由题意得:
5x+6=y
6x-5=y
古有一捕快,一天晚上他在野外的一个茅屋里,听到外边来了一群人在吵闹,他隐隐约约地听到几个声音,下面有这一古诗为证:
解得:
x=11
y=61
答:有11个人,61两银.
布置作业
请完成对应习题
8.3 实际问题与二元一次方程组
1.能够根据具体的数量关系,列出二元一次方程
组解决简单的实际问题;(重点)
2.学会利用二元一次方程组解决几何、行程问题.
(重点、难点)
学习目标
新课讲解
合作与交流
问题1 题中有哪些未知量,你如何设未知数?
未知量:每头大牛1天需用的饲料;
每头小牛1天需用的饲料.
问题2 题中有哪些等量关系?
(1)30只大牛和15只小牛一天需用饲料为675kg;
(2)(30+12)只大牛和(15+5)只小牛一天需用饲料为940kg.
设未知数:设每头大牛和每头小牛平均1天各需用饲料为xkg和ykg,
新课讲解
解:设每头大牛和小牛平均1天各需用饲料为xkg和ykg,
根据等量关系,列方程组:
答:每头大牛和每头小牛1天各需用饲料为20kg和5kg,饲养员李大叔估计每天大牛需用饲料18到20千克,每头小牛一天需用7到8千克与计算有一定的出入.
+ = 675,
+ = 940.
30x
15y
42x
20y
解方程组: x= ,
y= .
20
5
新课讲解
剧情发展:随着养牛场规模逐渐扩大,李大叔需聘请饲养员协助管理现有的42头大牛和20头小牛,已知甲种饲养员每人可负责8头大牛和4头小牛,乙种饲养员每人可负责5头大牛和2头小牛,请问李大叔应聘请甲、乙两种饲养员各多少人?
解:设李大叔应聘请甲种饲养员x人,乙种饲养员y人,则:
+ = 42,
+ = 20.
8x
5y
4x
2y
解得:
x =4
y = 2
答:李大叔应聘请甲种饲养员4人,乙种饲养员2人.
新课讲解
典例精析
例1 某市举办中学生足球比赛,规定胜一场得3分,平一场得1分.市第二中学足球队比赛11场,没有输过一场,共得27分,试问该队胜几场?平几场?
分析:题中的未知量有胜的场数和平的场数,等量关系有:胜的场数+平的场数=11;
胜场得分+平场得分=27.
胜场
平场
合计
场数
得分
x
3x
y
y
11
27
新课讲解
解:设市第二中学足球队胜x场,平y场.依题意可得
8
y
3x
y
3
答:该市第二中学足球队胜8场,平3场.
x
通过上述两题,总结
用二元一次方程组解
决实际问题的步骤
新课讲解
解题小结:用二元一次方程组解决实际问题的步骤:
(1)审题:弄清题意和题目中的_________;
(2)设元:用___________表示题目中的未知数;
(3)列方程组:根据___个等量关系列出方程组;
(4)解方程组:利用____________或___________解
出未知数的值;
(5)检验并答:检验所求的解是否符合实际意义,
然后作答.
总结归纳
数量关系
字母
2
代入消元法
加减消元法
新课讲解
练一练1:某城市规定:出租车起步价所包含的路程为0~3km,超过3km的部分按每千米另收费.
甲说:“我乘这种出租车走了11km,付了17元.”
乙说:“我乘这种出租车走了23km,付了35元.”
请你算一算:出租车的起步价是多少元?超过3km后,每千米的车费是多少元?
分析 本问题涉及的等量关系有:
总车费=0~3km的车费(起步价)+超过3km的车费.
新课讲解
解 设出租车的起步价是x元,超过3km后每千米收费y元.
根据等量关系,得
解这个方程组,得
答:这种出租车的起步价是5元,超过3km后每千米收费1.5元.
起步价
超过3km后的费用
合计费用
甲
乙
x
x
(11-3)y
(23-3)y
17
35
新课讲解
练一练2:今有牛五、羊二,直金十两.牛二、羊五,直金八两.牛、羊各直金几何?
牛五、羊二
牛二、羊五
新课讲解
5头牛、2只羊共价值10两“金”;2头牛、5只羊共价值8两“金”.问每头牛、每只羊各价值多少“金”?
题目大意
解:设每头牛值“金”x两,每只羊值“金”y两,
由题意,得
5x+2y=10,
2x+5y=8.
解得
x=
y=
{
答:羊值“金” 两,牛值“金” 两.
新课讲解
知识点2 列方程组解决几何问题
据统计资料,甲、乙两种作物的单位面积产量的比是1:2.现要把一块长200m、宽100m的长方形土地,分为两块小长方形土地,分别种植这两种作物.怎样划分这块土地,使甲、乙两种作物的总产量的比是3:4?
请提取数学信息
新课讲解
转换成数学语言:
A
D
C
B
已知:长方形ABCD, AB=CD=200m,AD=BC=100m,长方形ABCD分割为两个小长方形,长方形1和长方形2分别种甲、乙作物,甲、乙单位面积产量的比是1:2.
目标:甲、乙两种作物的总产量的比是3:4
新课讲解
这里研究的实际上是 什么 问题.
分
析
把一个长方形分成两个小长方形有哪些分割方式?
01
竖着画,把长分成两段,则宽不变
02
横着画,把宽分成两段,则长不变
长方形的面积分割
我们可以画出示意图来帮助分析
试着画一画
新课讲解
01
竖着画,把长分成两段,则宽不变
A
D
C
F
B
E
1.大长方形的长=200m
2.甲、乙两种作物总产量比=3:4
等量关系式有几个?
分
析
新课讲解
01
竖着画,把长分成两段,则宽不变
A
D
C
F
B
E
1.大长方形的长=200m
2.甲、乙两种作物总产量比=3:4
分
析
设AE=xm,BE=ym.
先求出两种作物的面积
SAEFD=100x
SEFCB=100y
再写出两种作物的总产量
甲:100x×1
乙:100y×2
则列方程为
100x:200y=3:4
总产量=
?
1 : 2
x
y
200m
100
如何设未知数呢?
则列方程为
x+y=200
单位面积产量×面积
新课讲解
01
竖着画,把长分成两段,则宽不变
A
D
C
F
B
E
根据题意列方程组为
100x:200y=3:4
x
y
200m
100m
解
答
x+y=200
解得
x=120
y=80
你觉得该如何答题比较完整呢?
甲种作物
乙种作物
解:
过点E作EF⊥AB,
交CD于点F.
设AE=xm,BE=ym.
答:将这块土地分为长120m,宽100m和长100m,宽80m的
两个小长方形分别种植甲、乙两种作物.
新课讲解
02
横着画,把宽分成两段,则长不变
A
D
C
B
E
x
y
F
x+y=100
乙种作物
甲种作物
解:过点E作EF⊥AD,交BC于点F.
设DE=xm,AE=ym.
200x:400y=3:4
200y
200x
x=60
y=40
解得
解
答
根据题意列方程组为
200m
100m
答:将这块土地分为长200m,宽60m和长200m,宽40m的
两个小长方形分别种植甲、乙两种作物.
新课讲解
练一练: 如图,8块相同的小长方形地砖拼成一个大长方形,每块小长方形地砖的长和宽分别是多少?(单位:cm)
60
x+y=60
x=3y
解:设小长方形地砖的长为x, 宽为y,
由题意,得
解此方程组得:
x =45,
y=15.
答:小长方形地砖的长为45cm, 宽为15cm.
新课讲解
知识点3 列方程组解决行程问题
小华从家里到学校的路是一段平路和一段下坡路. 假设他始终保持平路每分钟走60m,下坡路每分钟走80m,上坡路每分钟走40m,则他从家里到学校需10min,从学校到家里需15min.问小华家离学校多远?
新课讲解
分析:小华到学校的路分成两段,一段为平路,
一段为下坡路.
平路:60 m/min
下坡路:80 m/min
上坡路:40 m/min
走平路的时间+走下坡路的时间=________,
走上坡路的时间+走平路的时间= _______.
路程=平均速度×时间
10
15
新课讲解
方法一(直接设元法)
平路时间
坡路时间
总时间
上学
放学
解:设小华家到学校平路长x m,下坡路长y m.
根据题意,可列方程组:
解方程组,得
所以,小明家到学校的距离为700m.
新课讲解
方法二(间接设元法)
平路
距离
坡路距离
上学
放学
解:设小华下坡路所花时间为xmin,上坡路所花时间为ymin.
根据题意,可列方程组:
解方程组,得
所以,小明家到学校的距离为700m.
故 平路距离:60×(10-5)=300(m)
坡路距离:80×5=400(m)
新课讲解
例2 甲、乙两人相距4km,以各自的速度同时出发.如果同向而行,甲2h追上乙;如果相向而行,两人0.5h后相遇.试问两人的速度各是多少?
典例精析
分析:对于行程问题,一般可以借助示意图表示题中的数量关系,可以更加直观的找到相等关系.
新课讲解
(1) 同时出发,同向而行
甲出发点
乙出发点
4km
甲追上乙
乙2h行程
甲2h行程
甲2h行程=4km+乙2h行程
(2) 同时出发,相向而行
甲出发点
乙出发点
4km
相遇地
甲0.5h
行程
乙0.5h
行程
甲0.5h行程+乙0.5h行程=4km
新课讲解
解:设甲、乙的速度分别为xkm/h,ykm/h.
根据题意,得
解方程组,得
答:甲的速度为5km/h,乙的速度为3km/h.
新课讲解
练一练:我国的长江由西至东奔腾不息,其中九江至南京约有450千米的路程,某船从九江出发9小时就能到达南京;返回时则用多了1小时.求此船在静水中的速度以及长江水的平均流速.
解:设轮船在静水中的速度为x千米/时,长江水的平均流速为y千米/时.
答:轮船在静水中的速度为47.5千米/时,长江水的平均流速为2.5千米/时.
课堂小结
二元一次方程组的应用
应用
步骤
简单实际问题
行程问题
路程=平均速度×时间
审题:弄清题意和题目中的
设元:用_____表示题目中的未知数
列方程组:根据__个等量关系列出方程组
解方程组
检验作答
数量关系
字母
2
代入法;
加减法.
几何问题
当堂小练
1.计划若干节车皮装运一批货物.如果每节装15.5吨,则有4吨装不下,如果每节装16.5吨,则还可多装8吨.问有多少节车皮?多少吨货物?
解:设有x节车皮,y吨货物,根据题意列出方程组得
y=15.5x+4,
y=16.5x-8.
(以下部分由同学们完成)
当堂小练
2.某班有40名同学看演出,购买甲、乙两种票共用去370元,其中甲种票每张10元,乙种票每张8元.请问甲种和乙种票各多少张?
解得
答:甲种票25张,乙种票15张.
当堂小练
3.课本中介绍我国古代数学名著《孙子算经》上有这样的一道题:今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各多少只?
解得
答:鸡有23只,兔有12只.
当堂小练
4.有甲、乙两数,甲数的3倍与乙数的2倍之和等于47,甲数的5倍比乙数的6倍小1,这两个数分别是多少?
解得
答:甲数为10,乙数为 .
拓展与延伸
隔壁听到人分银,
不知人数不知银.
每人五两多六两,
每人六两少五两.
多少人数多少银?
解:设有x个人,y两银,
由题意得:
5x+6=y
6x-5=y
古有一捕快,一天晚上他在野外的一个茅屋里,听到外边来了一群人在吵闹,他隐隐约约地听到几个声音,下面有这一古诗为证:
解得:
x=11
y=61
答:有11个人,61两银.
布置作业
请完成对应习题
