人教版八年级下册17.1.3勾股定理在数轴上表示根号13 (共14张ppt)
文档属性
| 名称 | 人教版八年级下册17.1.3勾股定理在数轴上表示根号13 (共14张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 377.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-20 00:00:00 | ||
图片预览



文档简介
(共14张PPT)
在数学中也有这样一幅美丽的“海螺型”图案
第七届国际数学
教育大会的会徽
数学海螺图:
ICME—7
(一)创设情境
点击添加文本
点击添加文本
点击添加文本
点击添加文本
添加文本
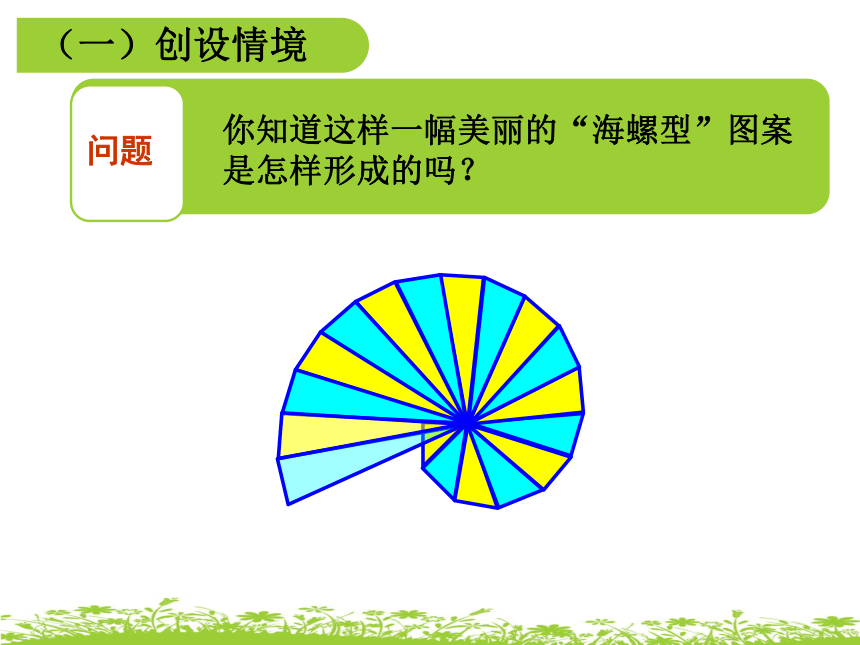
(一)创设情境
你知道这样一幅美丽的“海螺型”图案是怎样形成的吗?
问题
17.1
勾股定理(第3课时)
人教版
八年级下册
——在数轴上表示
点击添加文本
点击添加文本
点击添加文本
点击添加文本
添加文本
学习目标:
1.
会在数轴上画出表示
(n为正整数)的点.
在用勾股定理解决问题的过程中,学会构造
出符合条件的直角三角形,体会数形结合的
数学思想的应用.
点击添加文本
点击添加文本
点击添加文本
点击添加文本
添加文本
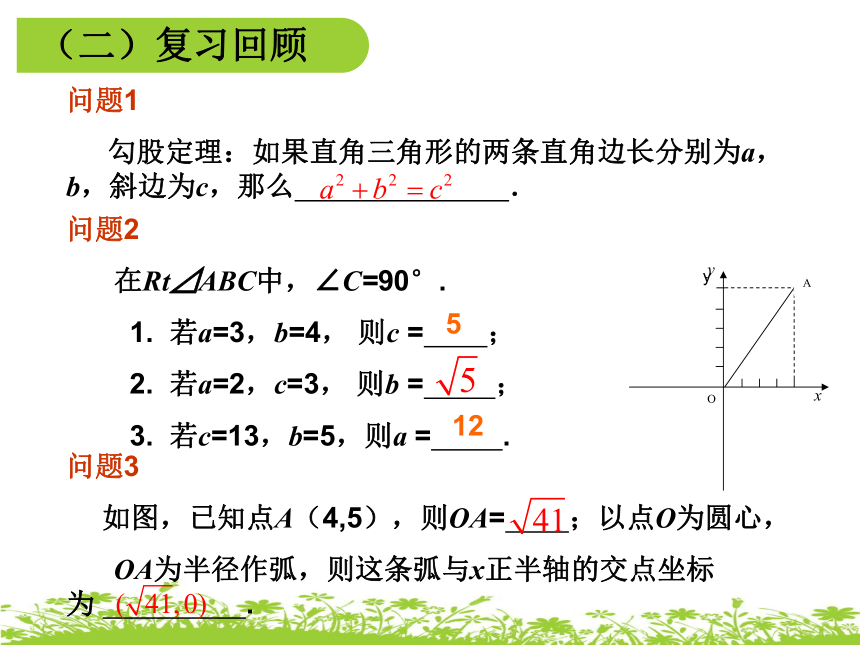
(二)复习回顾
问题2
在Rt⊿ABC中,∠C=90°.
1.
若a=3,b=4,
则c
=
;
2.
若a=2,c=3,
则b
=
;
3.
若c=13,b=5,则a
=
.
x
O
A
y
y
问题3
如图,已知点A(4,5),则OA=
;以点O为圆心,
OA为半径作弧,则这条弧与x正半轴的交点坐标为
.
问题1
勾股定理:如果直角三角形的两条直角边长分别为a,b,斜边为c,那么
.
5
12
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
O
A
B
C
D
E
F
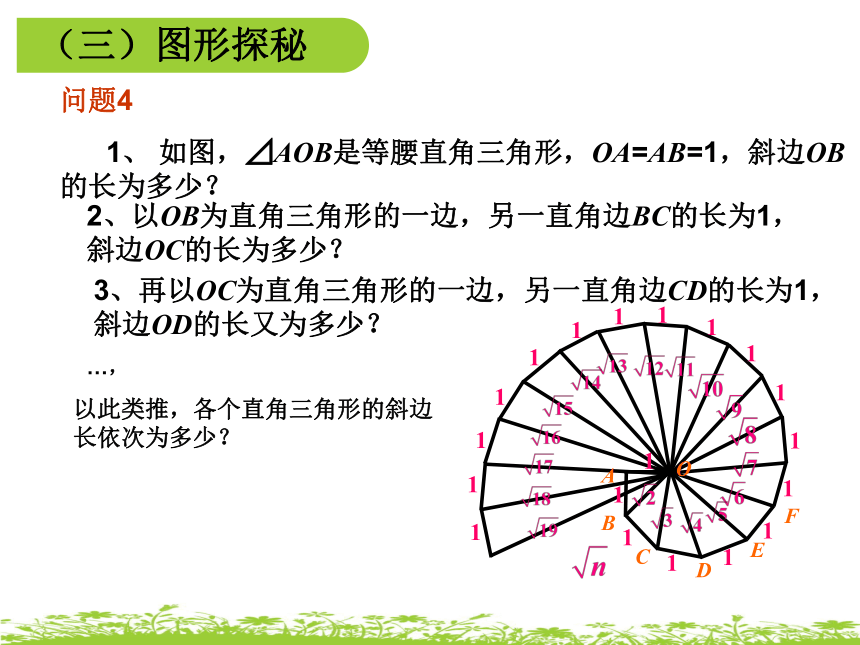
(三)图形探秘
问题4
1、
如图,⊿AOB是等腰直角三角形,OA=AB=1,斜边OB的长为多少?
2、以OB为直角三角形的一边,另一直角边BC的长为1,斜边OC的长为多少?
3、再以OC为直角三角形的一边,另一直角边CD的长为1,斜边OD的长又为多少?
…,
以此类推,各个直角三角形的斜边长依次为多少?
点击添加文本
点击添加文本
点击添加文本
点击添加文本
添加文本
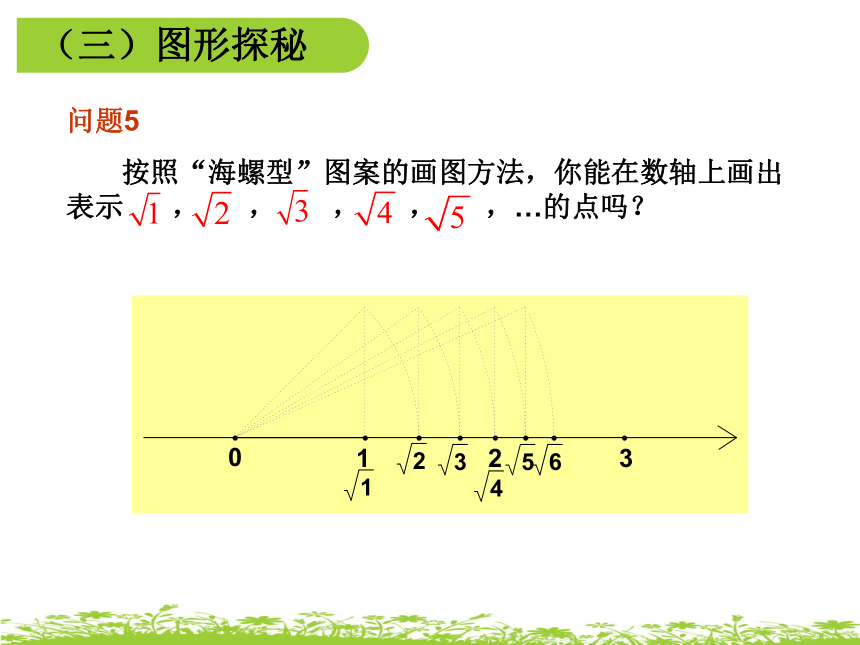
(三)图形探秘
问题5
按照“海螺型”图案的画图方法,你能在数轴上画出表示
,
,
,
,
,…的点吗?
点击添加文本
点击添加文本
点击添加文本
点击添加文本
添加文本
(四)操作应用
问题6
前面我们根据“海螺型”图案的画图过程,学会了在数轴上画出表示
的点方法,你能用更为简便的方法在数轴上画出表示
的点吗?
(1)若一直角三角形的两直角边分别为a,b,斜边c
=
.
当a=1时,b=
;
当a=2时,b=
;
③
当a=3时,b=
.
(2)请结合对问题(1)的思考,在数轴上画出表示
的点,并叙述作图方法.
3
2
0
1
2
3
4
步骤:
l
A
B
C
1.在数轴上取点A,使OA=3;
2.过点A作直线l⊥OA,在l上取一点B,使AB=2;
3.以原点O为圆心,以OB为半径作弧,弧与数轴交于C点,则点C即为表示
的点.
你能在数轴上画出表示
的点吗?
(四)操作应用
√
0
1
2
3
4
A
B
C
(四)操作应用
问题7
你能用简便方法在数轴上画出表示
的点吗?
l
则点C即为表示
的点.
问题8
如图为4×4的正方形网格,以格点和点A为端点,你能画出几条长为
的线段?
A
(四)操作应用
点击添加文本
点击添加文本
点击添加文本
点击添加文本
添加文本
(五)课堂小结
问题10
(1)本节课学习了哪些内容?
(2)本节课学习过程中运用了哪些数学思想方法?
构造法;
数形结合的数学思想.
勾股定理的应用
①在数轴上画出表示
(n为正整数)的点
;
②在网格中画出长为
(n为正整数)的线段.
点击添加文本
点击添加文本
点击添加文本
点击添加文本
添加文本
(六)布置作业
教材p27练习题1,习题17.1第6题.
点击添加文本
点击添加文本
点击添加文本
点击添加文本
添加文本
祝同学们学业进步!
在数学中也有这样一幅美丽的“海螺型”图案
第七届国际数学
教育大会的会徽
数学海螺图:
ICME—7
(一)创设情境
点击添加文本
点击添加文本
点击添加文本
点击添加文本
添加文本
(一)创设情境
你知道这样一幅美丽的“海螺型”图案是怎样形成的吗?
问题
17.1
勾股定理(第3课时)
人教版
八年级下册
——在数轴上表示
点击添加文本
点击添加文本
点击添加文本
点击添加文本
添加文本
学习目标:
1.
会在数轴上画出表示
(n为正整数)的点.
在用勾股定理解决问题的过程中,学会构造
出符合条件的直角三角形,体会数形结合的
数学思想的应用.
点击添加文本
点击添加文本
点击添加文本
点击添加文本
添加文本
(二)复习回顾
问题2
在Rt⊿ABC中,∠C=90°.
1.
若a=3,b=4,
则c
=
;
2.
若a=2,c=3,
则b
=
;
3.
若c=13,b=5,则a
=
.
x
O
A
y
y
问题3
如图,已知点A(4,5),则OA=
;以点O为圆心,
OA为半径作弧,则这条弧与x正半轴的交点坐标为
.
问题1
勾股定理:如果直角三角形的两条直角边长分别为a,b,斜边为c,那么
.
5
12
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
O
A
B
C
D
E
F
(三)图形探秘
问题4
1、
如图,⊿AOB是等腰直角三角形,OA=AB=1,斜边OB的长为多少?
2、以OB为直角三角形的一边,另一直角边BC的长为1,斜边OC的长为多少?
3、再以OC为直角三角形的一边,另一直角边CD的长为1,斜边OD的长又为多少?
…,
以此类推,各个直角三角形的斜边长依次为多少?
点击添加文本
点击添加文本
点击添加文本
点击添加文本
添加文本
(三)图形探秘
问题5
按照“海螺型”图案的画图方法,你能在数轴上画出表示
,
,
,
,
,…的点吗?
点击添加文本
点击添加文本
点击添加文本
点击添加文本
添加文本
(四)操作应用
问题6
前面我们根据“海螺型”图案的画图过程,学会了在数轴上画出表示
的点方法,你能用更为简便的方法在数轴上画出表示
的点吗?
(1)若一直角三角形的两直角边分别为a,b,斜边c
=
.
当a=1时,b=
;
当a=2时,b=
;
③
当a=3时,b=
.
(2)请结合对问题(1)的思考,在数轴上画出表示
的点,并叙述作图方法.
3
2
0
1
2
3
4
步骤:
l
A
B
C
1.在数轴上取点A,使OA=3;
2.过点A作直线l⊥OA,在l上取一点B,使AB=2;
3.以原点O为圆心,以OB为半径作弧,弧与数轴交于C点,则点C即为表示
的点.
你能在数轴上画出表示
的点吗?
(四)操作应用
√
0
1
2
3
4
A
B
C
(四)操作应用
问题7
你能用简便方法在数轴上画出表示
的点吗?
l
则点C即为表示
的点.
问题8
如图为4×4的正方形网格,以格点和点A为端点,你能画出几条长为
的线段?
A
(四)操作应用
点击添加文本
点击添加文本
点击添加文本
点击添加文本
添加文本
(五)课堂小结
问题10
(1)本节课学习了哪些内容?
(2)本节课学习过程中运用了哪些数学思想方法?
构造法;
数形结合的数学思想.
勾股定理的应用
①在数轴上画出表示
(n为正整数)的点
;
②在网格中画出长为
(n为正整数)的线段.
点击添加文本
点击添加文本
点击添加文本
点击添加文本
添加文本
(六)布置作业
教材p27练习题1,习题17.1第6题.
点击添加文本
点击添加文本
点击添加文本
点击添加文本
添加文本
祝同学们学业进步!
