人教版八年级下册17.1第二课时利用勾股定理解决平面几何问题(共19张ppt)
文档属性
| 名称 | 人教版八年级下册17.1第二课时利用勾股定理解决平面几何问题(共19张ppt) |
|
|
| 格式 | zip | ||
| 文件大小 | 355.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-20 00:00:00 | ||
图片预览


文档简介
(共19张PPT)
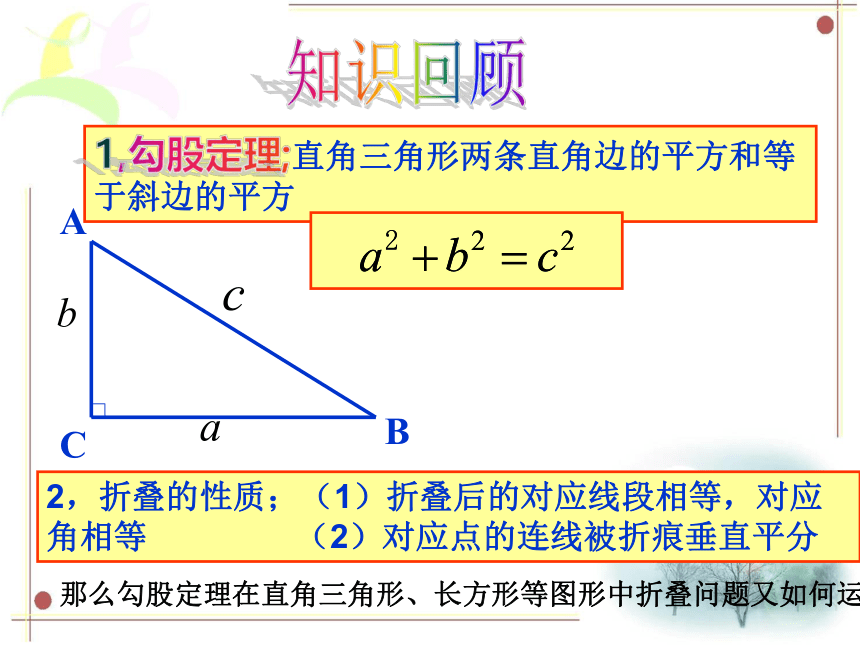
勾股定理
在折叠问题中的应用
A
B
C
D
G
F
E
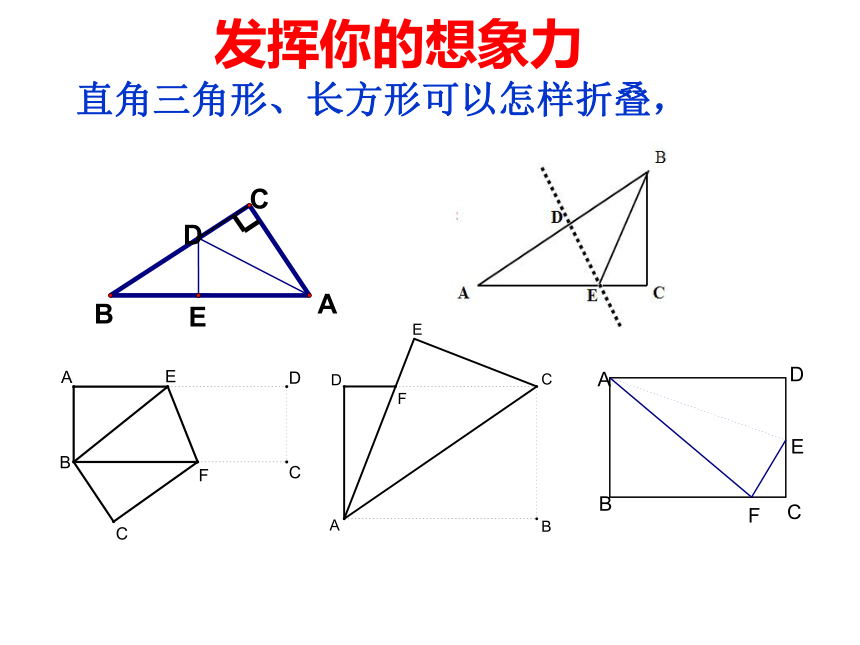
1,勾股定理;直角三角形两条直角边的平方和等于斜边的平方
知识回顾
那么勾股定理在直角三角形、长方形等图形中折叠问题又如何运用呢?
B
C
A
2,折叠的性质;(1)折叠后的对应线段相等,对应角相等
(2)对应点的连线被折痕垂直平分
发挥你的想象力
直角三角形、长方形可以怎样折叠,
C
B
A
D
E
A
C
B
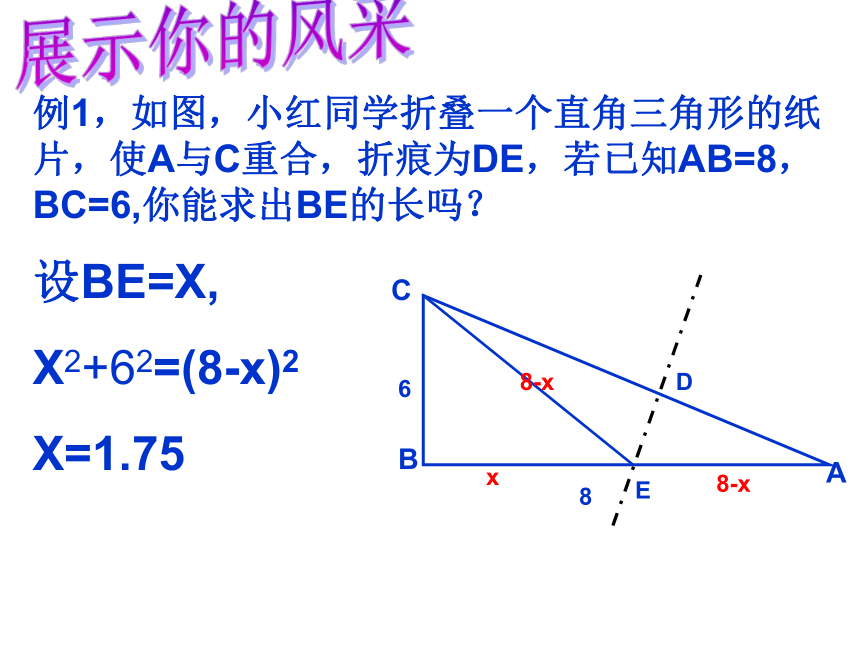
例1,如图,小红同学折叠一个直角三角形的纸片,使A与C重合,折痕为DE,若已知AB=8,BC=6,你能求出BE的长吗?
D
E
6
8
x
8-x
8-x
展示你的风采
设BE=X,
X2+62=(8-x)2
X=1.75
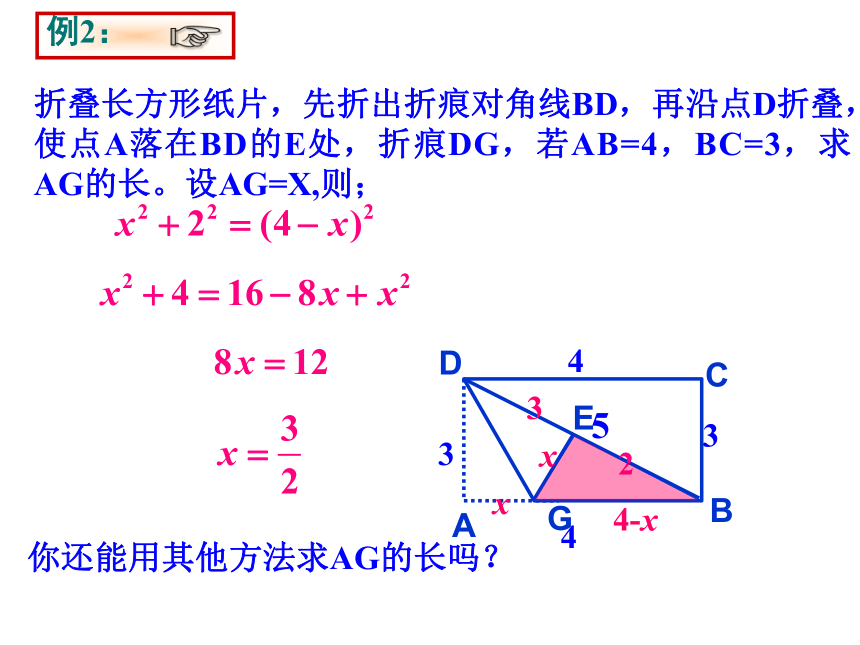
折叠长方形纸片,先折出折痕对角线BD,再沿点D折叠,使点A落在BD的E处,折痕DG,若AB=4,BC=3,求AG的长。设AG=X,则;
D
A
G
B
C
E
例2:
?
4
x
3
4
3
4-x
x
3
你还能用其他方法求AG的长吗?
折叠长方形纸片,先折出折痕对角线BD,再沿点D折叠,使点A落在BD的E处,折痕DG,若AB=4,BC=3,求AG的长。
D
A
G
B
C
E
4
x
3
4
3
4-x
x
3
你还能用其他方法求AG的长吗?
请问;这两种解法用的是什么方法?
面积法
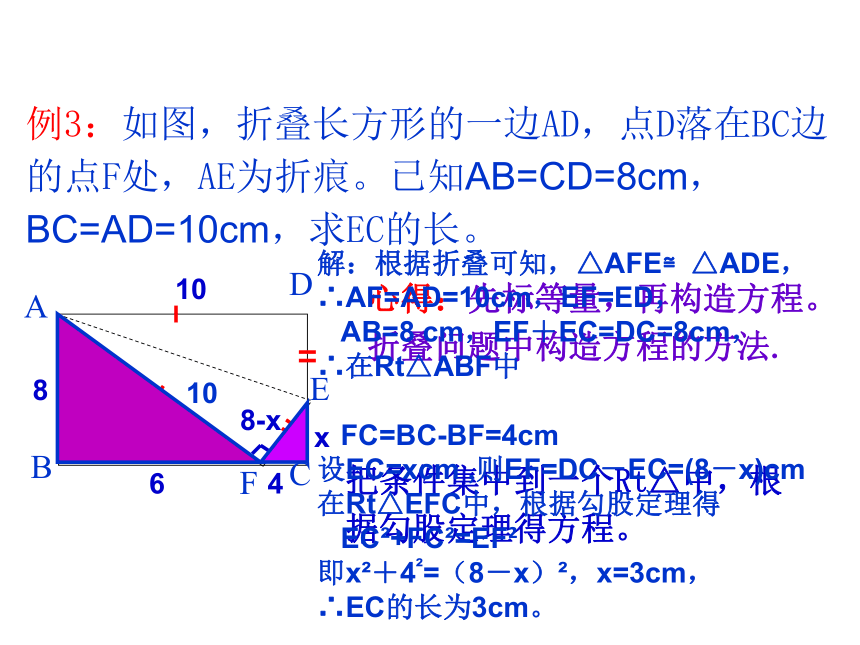
例3:如图,折叠长方形的一边AD,点D落在BC边
的点F处,AE为折痕。已知AB=CD=8cm,BC=AD=10cm,求EC的长。
A
B
C
D
F
E
8
10
10
6
x
4
8-x
心得:先标等量,再构造方程。
折叠问题中构造方程的方法.
把条件集中到一个Rt△中,根据勾股定理得方程。
解:根据折叠可知,△AFE≌△ADE,
∴AF=AD=10cm,EF=ED,
AB=8
cm,EF+EC=DC=8cm,
∴在Rt△ABF中
FC=BC-BF=4cm
设EC=xcm
,则EF=DC-EC=(8-x)cm
在Rt△EFC中,根据勾股定理得
EC?+FC?=EF?
即x?+4?=(8-x)?,x=3cm,
∴EC的长为3cm。
10
例4、如图,把长方形纸片ABCD折叠,使顶点A与顶点C重合在一起,EF为折痕。若AB=9,BC=3,试求折痕EF的长。
A
B
C
D
G
F
E
H
9
3
x
9-x
9-x
x2+32=(9-x)2
x=4
9-x=5
解:设BF=X在在R
t
△FBC中,
根据勾股定理FC2=FB2+BC2
5
5
4
1
3
本题还有其他解法?如有,怎么解?
例4、如图,把长方形纸片ABCD折叠,使顶点A与顶点C重合在一起,EF为折痕。若AB=9,BC=3,试求EF的长。
学生探究,教师点拨。
例4、如图,把长方形纸片ABCD折叠,使顶点A与顶点C重合在一起,EF为折痕。若AB=9,BC=3,试求EF的长。
学生探究,教师点拨。
思绪飞扬:
1,三角形ABC是等腰三角形AB=AC=13,BC=10,将AB向AC方向对折,再将CD折叠到CA边上,折痕为CE,求三角形ACE的面积
A
B
C
D
A
D
C
D
C
A
D1
E
13
5
12
5
12-x
5
x
x
8
2、如图,一块直角三角形的纸片,两直角边AC=6㎝,BC=8㎝。现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,求CD的长.
A
C
D
B
E
第8题图
D
x
6
x
8-x
4
6
3,折叠矩形ABCD的一边AD,点D落在BC边上的点F处,已知AB=8CM,BC=10CM,求
1.CF
2.EC.
A
B
C
D
E
F
8
10
10
6
X
8-X
4
8-X
A
M
N
P
Q
30°
160
80
E
我们一起来探究
例,如图,公路MN和小路PQ在P处交汇,∠QPN=30°,点A处有一所学校,AP=160m,假设拖拉机行使时,周围100m内受噪音影响,那么拖拉机在公路MN上以18km/h的速度沿PN方向行驶时,学校是否受到噪音的影响?如果学校受到影响,那么受影响将持续多长时间?
A
M
N
P
Q
B
D
E
例,如图,公路MN和小路PQ在P处交汇,∠QPN=30°,点A处有一所学校,AP=160m,假设拖拉机行使时,周围100m内受噪音影响,那么拖拉机在公路MN上以18km/h的速度沿PN方向行驶时,学校是否受到噪音的影响?如果学校受到影响,那么受影响将持续多长时间?
A
M
N
P
Q
30°
B
D
160
08
E
100
60
60
100
如图,公路MN和小路PQ在P处交汇,∠QPN=30°,点A处有一所学校,AP=160m,假设拖拉机行使时,周围100m内受噪音影响,那么拖拉机在公路MN上以18km/h的速度沿PN方向行驶时,学校是否受到噪音的影响?如果学校受到影响,那么受影响将持续多长时间?
解题步骤;
1、标已知,标问题,明确目标在哪个直角三角形中,设适当的未知数x。
2、利用折叠,找全等。
3、将已知边和未知边(用含x的代数式表示)转化到同一直角三角形中表示出来。
4、利用勾股定理,列出方程,解方程,得解。
画龙点睛
(一)过程,步骤
1、标已知;
2、找相等;
3、设未知,利用勾股定理,列方程;
4、解方程,得解。
(二)思想方法;方程的思想
小结
期末复习专题;
(勾股定理在折叠中的应用)
作业
勾股定理
在折叠问题中的应用
A
B
C
D
G
F
E
1,勾股定理;直角三角形两条直角边的平方和等于斜边的平方
知识回顾
那么勾股定理在直角三角形、长方形等图形中折叠问题又如何运用呢?
B
C
A
2,折叠的性质;(1)折叠后的对应线段相等,对应角相等
(2)对应点的连线被折痕垂直平分
发挥你的想象力
直角三角形、长方形可以怎样折叠,
C
B
A
D
E
A
C
B
例1,如图,小红同学折叠一个直角三角形的纸片,使A与C重合,折痕为DE,若已知AB=8,BC=6,你能求出BE的长吗?
D
E
6
8
x
8-x
8-x
展示你的风采
设BE=X,
X2+62=(8-x)2
X=1.75
折叠长方形纸片,先折出折痕对角线BD,再沿点D折叠,使点A落在BD的E处,折痕DG,若AB=4,BC=3,求AG的长。设AG=X,则;
D
A
G
B
C
E
例2:
?
4
x
3
4
3
4-x
x
3
你还能用其他方法求AG的长吗?
折叠长方形纸片,先折出折痕对角线BD,再沿点D折叠,使点A落在BD的E处,折痕DG,若AB=4,BC=3,求AG的长。
D
A
G
B
C
E
4
x
3
4
3
4-x
x
3
你还能用其他方法求AG的长吗?
请问;这两种解法用的是什么方法?
面积法
例3:如图,折叠长方形的一边AD,点D落在BC边
的点F处,AE为折痕。已知AB=CD=8cm,BC=AD=10cm,求EC的长。
A
B
C
D
F
E
8
10
10
6
x
4
8-x
心得:先标等量,再构造方程。
折叠问题中构造方程的方法.
把条件集中到一个Rt△中,根据勾股定理得方程。
解:根据折叠可知,△AFE≌△ADE,
∴AF=AD=10cm,EF=ED,
AB=8
cm,EF+EC=DC=8cm,
∴在Rt△ABF中
FC=BC-BF=4cm
设EC=xcm
,则EF=DC-EC=(8-x)cm
在Rt△EFC中,根据勾股定理得
EC?+FC?=EF?
即x?+4?=(8-x)?,x=3cm,
∴EC的长为3cm。
10
例4、如图,把长方形纸片ABCD折叠,使顶点A与顶点C重合在一起,EF为折痕。若AB=9,BC=3,试求折痕EF的长。
A
B
C
D
G
F
E
H
9
3
x
9-x
9-x
x2+32=(9-x)2
x=4
9-x=5
解:设BF=X在在R
t
△FBC中,
根据勾股定理FC2=FB2+BC2
5
5
4
1
3
本题还有其他解法?如有,怎么解?
例4、如图,把长方形纸片ABCD折叠,使顶点A与顶点C重合在一起,EF为折痕。若AB=9,BC=3,试求EF的长。
学生探究,教师点拨。
例4、如图,把长方形纸片ABCD折叠,使顶点A与顶点C重合在一起,EF为折痕。若AB=9,BC=3,试求EF的长。
学生探究,教师点拨。
思绪飞扬:
1,三角形ABC是等腰三角形AB=AC=13,BC=10,将AB向AC方向对折,再将CD折叠到CA边上,折痕为CE,求三角形ACE的面积
A
B
C
D
A
D
C
D
C
A
D1
E
13
5
12
5
12-x
5
x
x
8
2、如图,一块直角三角形的纸片,两直角边AC=6㎝,BC=8㎝。现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,求CD的长.
A
C
D
B
E
第8题图
D
x
6
x
8-x
4
6
3,折叠矩形ABCD的一边AD,点D落在BC边上的点F处,已知AB=8CM,BC=10CM,求
1.CF
2.EC.
A
B
C
D
E
F
8
10
10
6
X
8-X
4
8-X
A
M
N
P
Q
30°
160
80
E
我们一起来探究
例,如图,公路MN和小路PQ在P处交汇,∠QPN=30°,点A处有一所学校,AP=160m,假设拖拉机行使时,周围100m内受噪音影响,那么拖拉机在公路MN上以18km/h的速度沿PN方向行驶时,学校是否受到噪音的影响?如果学校受到影响,那么受影响将持续多长时间?
A
M
N
P
Q
B
D
E
例,如图,公路MN和小路PQ在P处交汇,∠QPN=30°,点A处有一所学校,AP=160m,假设拖拉机行使时,周围100m内受噪音影响,那么拖拉机在公路MN上以18km/h的速度沿PN方向行驶时,学校是否受到噪音的影响?如果学校受到影响,那么受影响将持续多长时间?
A
M
N
P
Q
30°
B
D
160
08
E
100
60
60
100
如图,公路MN和小路PQ在P处交汇,∠QPN=30°,点A处有一所学校,AP=160m,假设拖拉机行使时,周围100m内受噪音影响,那么拖拉机在公路MN上以18km/h的速度沿PN方向行驶时,学校是否受到噪音的影响?如果学校受到影响,那么受影响将持续多长时间?
解题步骤;
1、标已知,标问题,明确目标在哪个直角三角形中,设适当的未知数x。
2、利用折叠,找全等。
3、将已知边和未知边(用含x的代数式表示)转化到同一直角三角形中表示出来。
4、利用勾股定理,列出方程,解方程,得解。
画龙点睛
(一)过程,步骤
1、标已知;
2、找相等;
3、设未知,利用勾股定理,列方程;
4、解方程,得解。
(二)思想方法;方程的思想
小结
期末复习专题;
(勾股定理在折叠中的应用)
作业
