北师大版数学七年级下册2.1.1 对顶角、余角和补角 课件(25张)
文档属性
| 名称 | 北师大版数学七年级下册2.1.1 对顶角、余角和补角 课件(25张) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-19 21:53:38 | ||
图片预览








文档简介
第二章 相交线与平行线
1 两条直线的位置关系
课时1 对顶角、余角和补角
1.理解对顶角、补角、余角的概念;
2.掌握对顶角、补角、余角的性质,并能运用它们的
性质进行角的运算及一些实际问题.(重点、难点)
学习目标
新课导入
情境引入
新课导入
生活中处处可见道路、房屋、山川、桥梁.在大自然的杰作和人类的创造物中,蕴含着无数的相交线和平行线.
在同一平面内,两条直线的位置关系有相交和平行两种.若两条直线只有一个公共点,我们称这两条直线为相交线.在同一平面内,不相交的两条直线叫作平行线.
新课讲解
知识点1 对顶角的概念及性质
合作探究
如图,直线AB、CD相交于O,∠1和∠2有什么位置关系?
2
1
A
B
C
D
O
3
4
1.有公共顶点,
2.两边互为反向延长线.
新课讲解
请你观察图中∠1和∠2这组对顶角,你发现它们的大小有什么关系?
2
1
A
B
C
D
O
探究二:
∠1=∠2
对顶角相等
新课讲解
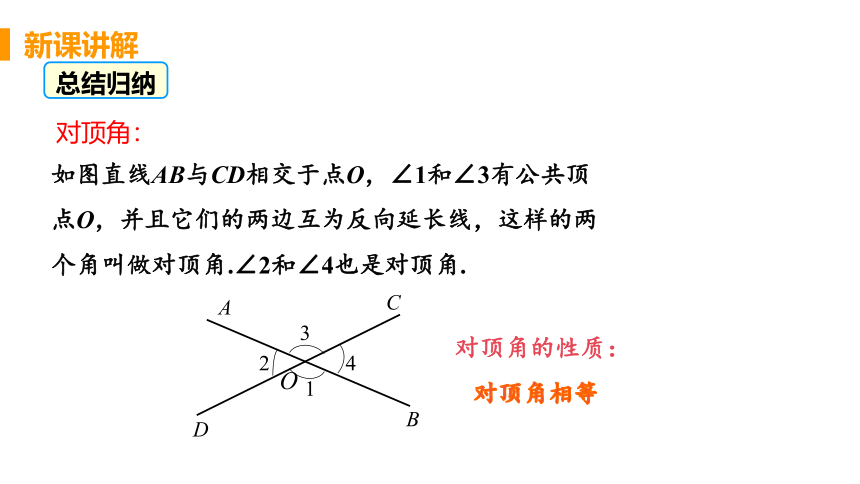
如图直线AB与CD相交于点O,∠1和∠3有公共顶点O,并且它们的两边互为反向延长线,这样的两个角叫做对顶角.∠2和∠4也是对顶角.
对顶角:
A
O
C
B
D
1
3
2
4
总结归纳
对顶角相等
对顶角的性质:
新课讲解
例1 下列各图中,∠1与∠2是对顶角的是( )
1
2
C
1
2
D
D
1
2
A
1
2
B
典例精析
方法总结:对顶角是由两条相交直线构成的,只有两条直线相交时,才能构成对顶角.
新课讲解
例2 如图,直线AB、CD,EF相交于点O,∠1=40°,∠BOC=110°,求∠2的度数.
解:因为∠1=40°,
∠BOC=110°(已知),
所以∠BOF=∠BOC-∠1
=110°-40°=70°.
因为∠BOF=∠2(对顶角相等),
所以∠2=70°(等量代换).
注意:隐含条件“对顶角相等”.
新课讲解
知识点2 补角和余角的概念
3
4
如果两个角的和等于180°(平角),就说这两个角互为补角(简称互补).可以说∠3是∠4的补角或∠4是∠3的补角.
定义:
新课讲解
2
1
如果两个角的和等于90°(直角),就说这两个角互为余角(简称互余).可以说∠1是∠2的余角或∠2是∠1的余角.
定义:
新课讲解
∠α
∠α的余角
∠α的补角
5°
32°
45°
77°
62°23′
27°37′
117°37′
85°
175°
58°
148°
45°
135°
103°
13°
x°(x<90)
90° x°
180° x°
同一个锐角的补角比它的余角大________.
做一做
90°
新课讲解
知识点3 补角和余角的性质
图1
N
2
D
C
O
1
3
4
A
B
图2
如图1,打台球时,选择适当的方向用白球击打红球,反弹后的红球会直接入袋,此时∠1=∠2,将图1简化成图2,ON与DC交于点O,∠DON=∠CON=900,∠1=∠2.
新课讲解
小组合作交流,解决下列问题:在图2中
问题1:哪些角互为补角?哪些角互为余角?
问题2:∠3与∠4有什么关系?为什么?
问题3:∠AOC与∠BOD有什么关系?为什么?
因为∠1= ∠2,
∠1+∠AOC=180°,
∠ 2+∠BOD=180°,
所以∠AOC=∠BOD.
同角(等角)的补角相等
N
2
D
C
O
1
3
4
A
B
图2
新课讲解
因为∠1= ∠2,
∠ 1+∠3=90° ,
∠ 2+∠4=90°,
所以 ∠ 3=∠4.
同角(等角)的余角相等
归纳总结:同角(等角)的补角相等,同角(等角)的余角相等.
N
2
D
C
O
1
3
4
A
B
图2
新课讲解
例3 如图,已知∠AOB在∠AOC内部,∠BOC=90°,OM、ON分别是∠AOB,∠AOC的平分线,∠AOB与∠COM互补,求∠BON的度数.
解:∵∠AOB与∠COM互补,
∴∠AOB+∠COM=180°,
即∠AOB+∠BOM+∠COB=180°.
∵∠COB=90°,
∴∠AOB+∠BOM=90°.
新课讲解
∵OM是∠AOB的平分线,
∴∠BOM= ∠AOB,即∠AOB+ ∠AOB=90°,解得∠AOB=60°,
∴∠AOC=∠BOC+∠AOB=90°+60°=150°.
∵ON平分∠AOC得∠AON= ∠AOC
= ×150°=75°.
由角的和差,
∴∠BON=∠AON-∠AOB
=75°-60°=15°.
互余
互补
两角间的数量关系
对应图形
性质
同角或等角的
余角相等
同角或等角的
补角相等
课堂小结
当堂小练
1.下列说法中,正确的有( )
①对顶角相等
②相等的角是对顶角
③不是对顶角的两个角就不相等
④不相等的角不是对顶角
A.1个 B.2个 C.3个 D.0个
B
√
√
当堂小练
2.判断下列各图中∠1和∠2是否为对顶角,并说明
理由?
1
2
1
2
1
2
1
2
1
2
1
2
√
×
×
×
×
×
当堂小练
3.图中给出的各角,哪些互为补角?
10o
30o
60o
80o
100o
120o
150o
170o
当堂小练
4.图中给出的各角,哪些互为余角?
15o
24o
66o
75o
46.2o
43.8o
当堂小练
5.如图,已知∠AOB=90°, ∠AOC= ∠BOD,则与
∠AOC互余的角有__________________.
∠BOC和 ∠AOD
拓展与延伸
6.如图已知:直线AB与CD交于点O, ∠EOD=900,
回答下列问题:
(1)∠AOE的余角是 ;补角是 ;
(2)∠AOC的余角是 ;补角是 ;
对顶角是 ;
C
A
B
D
O
E
∠AOC
∠BOE
∠AOE
∠BOC
∠BOD
布置作业
请完成对应习题
1 两条直线的位置关系
课时1 对顶角、余角和补角
1.理解对顶角、补角、余角的概念;
2.掌握对顶角、补角、余角的性质,并能运用它们的
性质进行角的运算及一些实际问题.(重点、难点)
学习目标
新课导入
情境引入
新课导入
生活中处处可见道路、房屋、山川、桥梁.在大自然的杰作和人类的创造物中,蕴含着无数的相交线和平行线.
在同一平面内,两条直线的位置关系有相交和平行两种.若两条直线只有一个公共点,我们称这两条直线为相交线.在同一平面内,不相交的两条直线叫作平行线.
新课讲解
知识点1 对顶角的概念及性质
合作探究
如图,直线AB、CD相交于O,∠1和∠2有什么位置关系?
2
1
A
B
C
D
O
3
4
1.有公共顶点,
2.两边互为反向延长线.
新课讲解
请你观察图中∠1和∠2这组对顶角,你发现它们的大小有什么关系?
2
1
A
B
C
D
O
探究二:
∠1=∠2
对顶角相等
新课讲解
如图直线AB与CD相交于点O,∠1和∠3有公共顶点O,并且它们的两边互为反向延长线,这样的两个角叫做对顶角.∠2和∠4也是对顶角.
对顶角:
A
O
C
B
D
1
3
2
4
总结归纳
对顶角相等
对顶角的性质:
新课讲解
例1 下列各图中,∠1与∠2是对顶角的是( )
1
2
C
1
2
D
D
1
2
A
1
2
B
典例精析
方法总结:对顶角是由两条相交直线构成的,只有两条直线相交时,才能构成对顶角.
新课讲解
例2 如图,直线AB、CD,EF相交于点O,∠1=40°,∠BOC=110°,求∠2的度数.
解:因为∠1=40°,
∠BOC=110°(已知),
所以∠BOF=∠BOC-∠1
=110°-40°=70°.
因为∠BOF=∠2(对顶角相等),
所以∠2=70°(等量代换).
注意:隐含条件“对顶角相等”.
新课讲解
知识点2 补角和余角的概念
3
4
如果两个角的和等于180°(平角),就说这两个角互为补角(简称互补).可以说∠3是∠4的补角或∠4是∠3的补角.
定义:
新课讲解
2
1
如果两个角的和等于90°(直角),就说这两个角互为余角(简称互余).可以说∠1是∠2的余角或∠2是∠1的余角.
定义:
新课讲解
∠α
∠α的余角
∠α的补角
5°
32°
45°
77°
62°23′
27°37′
117°37′
85°
175°
58°
148°
45°
135°
103°
13°
x°(x<90)
90° x°
180° x°
同一个锐角的补角比它的余角大________.
做一做
90°
新课讲解
知识点3 补角和余角的性质
图1
N
2
D
C
O
1
3
4
A
B
图2
如图1,打台球时,选择适当的方向用白球击打红球,反弹后的红球会直接入袋,此时∠1=∠2,将图1简化成图2,ON与DC交于点O,∠DON=∠CON=900,∠1=∠2.
新课讲解
小组合作交流,解决下列问题:在图2中
问题1:哪些角互为补角?哪些角互为余角?
问题2:∠3与∠4有什么关系?为什么?
问题3:∠AOC与∠BOD有什么关系?为什么?
因为∠1= ∠2,
∠1+∠AOC=180°,
∠ 2+∠BOD=180°,
所以∠AOC=∠BOD.
同角(等角)的补角相等
N
2
D
C
O
1
3
4
A
B
图2
新课讲解
因为∠1= ∠2,
∠ 1+∠3=90° ,
∠ 2+∠4=90°,
所以 ∠ 3=∠4.
同角(等角)的余角相等
归纳总结:同角(等角)的补角相等,同角(等角)的余角相等.
N
2
D
C
O
1
3
4
A
B
图2
新课讲解
例3 如图,已知∠AOB在∠AOC内部,∠BOC=90°,OM、ON分别是∠AOB,∠AOC的平分线,∠AOB与∠COM互补,求∠BON的度数.
解:∵∠AOB与∠COM互补,
∴∠AOB+∠COM=180°,
即∠AOB+∠BOM+∠COB=180°.
∵∠COB=90°,
∴∠AOB+∠BOM=90°.
新课讲解
∵OM是∠AOB的平分线,
∴∠BOM= ∠AOB,即∠AOB+ ∠AOB=90°,解得∠AOB=60°,
∴∠AOC=∠BOC+∠AOB=90°+60°=150°.
∵ON平分∠AOC得∠AON= ∠AOC
= ×150°=75°.
由角的和差,
∴∠BON=∠AON-∠AOB
=75°-60°=15°.
互余
互补
两角间的数量关系
对应图形
性质
同角或等角的
余角相等
同角或等角的
补角相等
课堂小结
当堂小练
1.下列说法中,正确的有( )
①对顶角相等
②相等的角是对顶角
③不是对顶角的两个角就不相等
④不相等的角不是对顶角
A.1个 B.2个 C.3个 D.0个
B
√
√
当堂小练
2.判断下列各图中∠1和∠2是否为对顶角,并说明
理由?
1
2
1
2
1
2
1
2
1
2
1
2
√
×
×
×
×
×
当堂小练
3.图中给出的各角,哪些互为补角?
10o
30o
60o
80o
100o
120o
150o
170o
当堂小练
4.图中给出的各角,哪些互为余角?
15o
24o
66o
75o
46.2o
43.8o
当堂小练
5.如图,已知∠AOB=90°, ∠AOC= ∠BOD,则与
∠AOC互余的角有__________________.
∠BOC和 ∠AOD
拓展与延伸
6.如图已知:直线AB与CD交于点O, ∠EOD=900,
回答下列问题:
(1)∠AOE的余角是 ;补角是 ;
(2)∠AOC的余角是 ;补角是 ;
对顶角是 ;
C
A
B
D
O
E
∠AOC
∠BOE
∠AOE
∠BOC
∠BOD
布置作业
请完成对应习题
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
