京改版九年级上册21.4圆周角(2) 教案(表格式)
文档属性
| 名称 | 京改版九年级上册21.4圆周角(2) 教案(表格式) |

|
|
| 格式 | zip | ||
| 文件大小 | 180.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-20 00:00:00 | ||
图片预览



文档简介
课程基本信息
课题
圆周角(2)
教科书
书名:《义务教育教科书.数学》
出版社:北京出版社
出版日期:2015年7月
教学目标
教学目标:
1.在探究圆周角定理的四个推论的过程中,进一步掌握圆心角、圆周角、所对弧和弦之间的关系;
2.引导学生在发现问题、提出问题并解决问题的过程中发展数学的学习能力;
3.在探究过程中培养学生的逻辑推理与合情推理能力及严谨求实的态度.
教学重点:探究圆周角定理的四个推论.
教学难点:在探究的过程中发展学生发现问题、提出问题、解决问题的能力.
教学过程
时间
教学环节
主要师生活动
1
分
钟
14
分
钟
4
分
钟
2
分
钟
复习
引入
探索
新知
练习巩固
课堂小结
作业提升
【活动一】
复习相关的知识:
1.圆周角的定义:顶点在圆上,且两边都与圆相交的角叫圆周角.
图1
图2
图3
2.圆周角定理:一条弧所对圆周角等于它所对的圆心角的一半.
3.在同圆或等圆中,如果两个圆心角、两条弧、两条弦中的一组量相等,那么它们所对应的其余各组量都分别相等.
4.思考:上面的定理中加入圆周角,它们之间又有怎样的关系?
【活动二】
1.请同学们在笔记本上画⊙O,画出所对的圆心角及圆周角.
预设:(所对的圆心角只有一个,但是圆周角
却有很多,先任取两个即∠ACB和∠ADB)
图4
2.问题:所对的圆周角,即∠C和∠D的大小有什么关系?
分析:根据圆周角定理“一条弧所对圆周角等于它所对的圆心角的一半”可知,
∠C和∠D都等于∠AOB的一半,因此,∠C和∠D是相等的.不仅如此,在这个圆中,所对的所有的圆周角都相等,它们都等于∠AOB的一半.请同学们用语言进行概括.
结论:同弧所对的圆周角相等.
3.问题:等弧所对的圆周角是否相等?
分析:(问题)如图4,如果等于,那么∠E和∠F相等吗?
从已知条件出发,弧AB等于弧CD可知,
等于所对的圆心角相等,即∠AOB=∠COD.
根据圆周角定理“一条弧所对圆周角等于它所对的圆心
角的一半”可得∠E=∠AOB,
∠F=∠COD,
由此可得∠E=∠F.
图5
结论:同弧或等弧所对的圆周角相等.
4.问题:相等的圆周角所对的弧是否相等呢,为什么?
预设:
图6
图7
图8
分析:如果是在同圆或者等圆中,根据圆周角和圆心角以及弧之间的关系,我们能够得到弧相等;如果不是同圆或者等圆呢?同学们可以动手画一画.
结论:在两个半径不相等的圆中,相等的圆周角所对的弧不相等.
结合以上的探究,可得:
推论1:同弧或等弧所对的圆周角相等;在同圆或等圆中,相等的圆周角所对的弧相等.
【活动三】
1.问题:同弧或等弧所对的圆周角相等,那么同弦或等弦所对的圆周角是否也相等?
2.画图:请同学们先在笔记本上画出同弦所对的两个圆周角.
预设:
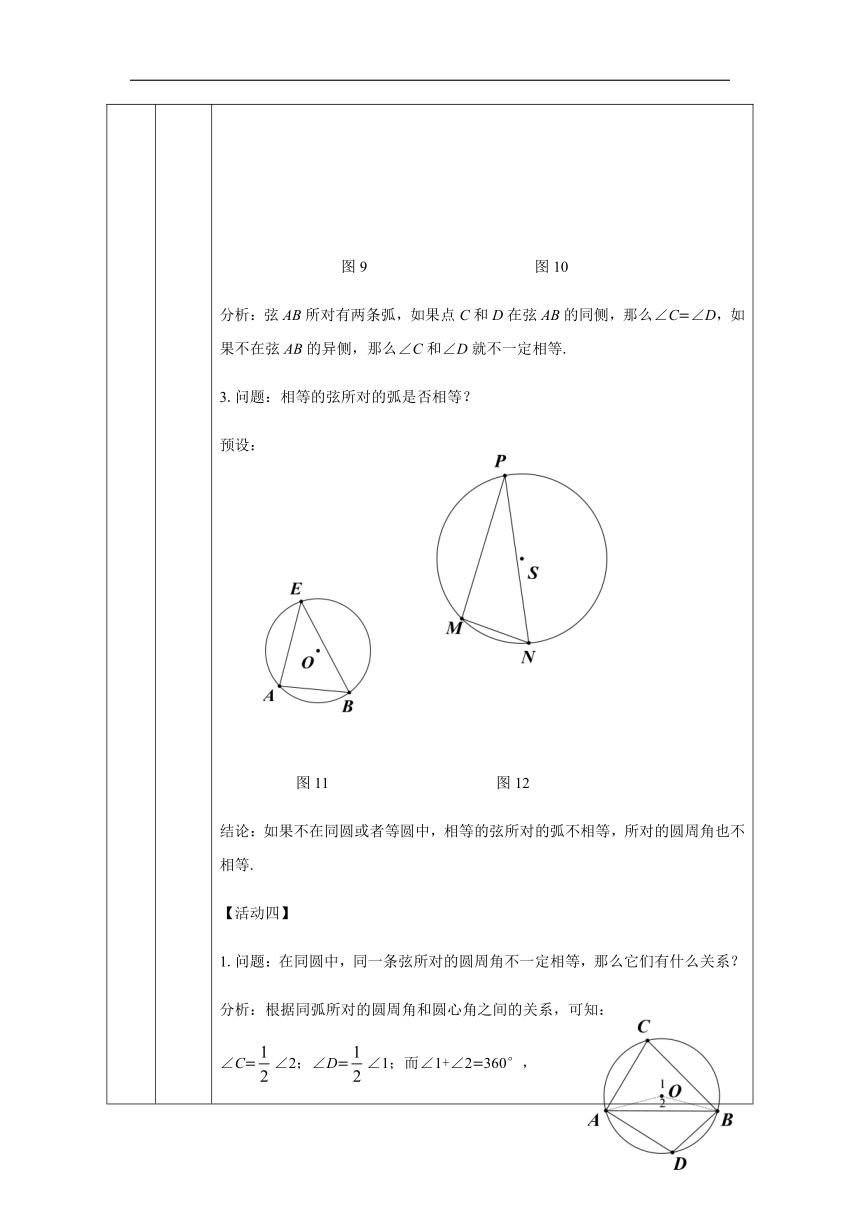
图9
图10
分析:弦AB所对有两条弧,如果点C和D在弦AB的同侧,那么∠C=∠D,如果不在弦AB的异侧,那么∠C和∠D就不一定相等.
3.问题:相等的弦所对的弧是否相等?
预设:
图11
图12
结论:如果不在同圆或者等圆中,相等的弦所对的弧不相等,所对的圆周角也不相等.
【活动四】
1.问题:在同圆中,同一条弦所对的圆周角不一定相等,那么它们有什么关系?
分析:根据同弧所对的圆周角和圆心角之间的关系,可知:
∠C=∠2;∠D=∠1;而∠1+∠2=360°,
所以∠C+∠D=180°,即:∠C和∠D互补.
图13
2.问题:在图13中,∠CAD和∠CBD有什么数量关系?
说明:四个顶点均在同一个圆上的四边形,叫做这个圆的内接四边形.
分析:圆内接四边形ACBD的内角和是360°,∠C和∠D互补,因此,∠CAD和∠CBD也是互补的.
推论2:圆内接四边形对角互补.
【活动五】
1.问题:如图14,∠C
和∠D有可能相等吗?什么时候相等?
分析:由于∠C+∠D
=180°,要使∠C
=∠D,
那么∠C和∠D就都等于90°,需要等于,
此时的两个弧也就是半圆,因此AB就是圆的直径.
由此可得:当AB是直径即和是半圆的时候,
∠C
和∠D相等,等于90°.
图14
推论3:半圆(或直径)所对的圆周角是直角.
从圆周角定理出发进行证明:
∵AB是⊙O的直径,
∴∠AOB
=180°,
∴∠C
=∠D
=∠AOB
=90°.
说明:反之,如果∠C等于90°,也可以得到∠AOB
等于180°,从而证得AB是直径.由此我们就得到了圆周角的第4条推论.
推论4:90°的圆周角所对弦是直径.
【活动六】
如图15,A,B,C,D是⊙O上的四个点,
(1)∠1=∠
______;∠2=∠
______.
(2)若∠1=∠2,你还能从图中找出哪些相等的量?
(3)若AC是直径,∠1=∠2,那么∠3=_______°.
图15
(4)若∠1+∠2=∠BAD=90°,那么AC______BD(填“>”、“<”、“=”).
【活动七】
1.知识小结:让我们一起回顾圆周角及其四个推论的探究过程:
圆周角定理:一条弧所对圆周角等于它所对的圆心角的一半.
圆周角不唯一
归纳共性
推论1:同弧或等弧所对的圆周角相等;
(反之)在同圆或等圆中,相等的圆周角所对的弧相等.
由等弧到等弦
由此及彼
推论2:圆内接四边形对角互补.
弦变直径
一般到特殊
推论3:
半圆(或直径)所对的圆周角是直角.
交换条件和结论
逆命题
推论4:
90°的圆周角所对弦是直径.
即:圆周角的四个推论探究的就是同弧或等弧的条件下,圆周角之间、所对的弦与圆周角之间的关系.
2.方法小结:通过归纳共性、改变条件、由特殊到一般或者由一般到特殊、得到逆命题等方法提出新的问题并加以探究.
A层:
1.已知,如图16,在⊙O中,AD是直径,BC是弦,
,
由这些条件你能推出哪些结论?(至少写出4个)
图16
2.将圆周角定理及其四个推论的条件和结论整理在笔记本上.
B层:
1.整理圆周角定理及四个推论,完善圆心角、圆周角、弧、弦之间的关系结构图.
2.如图17,在△ABC中,
AB=AC,以AB为直径作⊙O,
交BC于D,
交AC于E.
试说明∠BAD和∠EDC之间的数量关系.
图17
课题
圆周角(2)
教科书
书名:《义务教育教科书.数学》
出版社:北京出版社
出版日期:2015年7月
教学目标
教学目标:
1.在探究圆周角定理的四个推论的过程中,进一步掌握圆心角、圆周角、所对弧和弦之间的关系;
2.引导学生在发现问题、提出问题并解决问题的过程中发展数学的学习能力;
3.在探究过程中培养学生的逻辑推理与合情推理能力及严谨求实的态度.
教学重点:探究圆周角定理的四个推论.
教学难点:在探究的过程中发展学生发现问题、提出问题、解决问题的能力.
教学过程
时间
教学环节
主要师生活动
1
分
钟
14
分
钟
4
分
钟
2
分
钟
复习
引入
探索
新知
练习巩固
课堂小结
作业提升
【活动一】
复习相关的知识:
1.圆周角的定义:顶点在圆上,且两边都与圆相交的角叫圆周角.
图1
图2
图3
2.圆周角定理:一条弧所对圆周角等于它所对的圆心角的一半.
3.在同圆或等圆中,如果两个圆心角、两条弧、两条弦中的一组量相等,那么它们所对应的其余各组量都分别相等.
4.思考:上面的定理中加入圆周角,它们之间又有怎样的关系?
【活动二】
1.请同学们在笔记本上画⊙O,画出所对的圆心角及圆周角.
预设:(所对的圆心角只有一个,但是圆周角
却有很多,先任取两个即∠ACB和∠ADB)
图4
2.问题:所对的圆周角,即∠C和∠D的大小有什么关系?
分析:根据圆周角定理“一条弧所对圆周角等于它所对的圆心角的一半”可知,
∠C和∠D都等于∠AOB的一半,因此,∠C和∠D是相等的.不仅如此,在这个圆中,所对的所有的圆周角都相等,它们都等于∠AOB的一半.请同学们用语言进行概括.
结论:同弧所对的圆周角相等.
3.问题:等弧所对的圆周角是否相等?
分析:(问题)如图4,如果等于,那么∠E和∠F相等吗?
从已知条件出发,弧AB等于弧CD可知,
等于所对的圆心角相等,即∠AOB=∠COD.
根据圆周角定理“一条弧所对圆周角等于它所对的圆心
角的一半”可得∠E=∠AOB,
∠F=∠COD,
由此可得∠E=∠F.
图5
结论:同弧或等弧所对的圆周角相等.
4.问题:相等的圆周角所对的弧是否相等呢,为什么?
预设:
图6
图7
图8
分析:如果是在同圆或者等圆中,根据圆周角和圆心角以及弧之间的关系,我们能够得到弧相等;如果不是同圆或者等圆呢?同学们可以动手画一画.
结论:在两个半径不相等的圆中,相等的圆周角所对的弧不相等.
结合以上的探究,可得:
推论1:同弧或等弧所对的圆周角相等;在同圆或等圆中,相等的圆周角所对的弧相等.
【活动三】
1.问题:同弧或等弧所对的圆周角相等,那么同弦或等弦所对的圆周角是否也相等?
2.画图:请同学们先在笔记本上画出同弦所对的两个圆周角.
预设:
图9
图10
分析:弦AB所对有两条弧,如果点C和D在弦AB的同侧,那么∠C=∠D,如果不在弦AB的异侧,那么∠C和∠D就不一定相等.
3.问题:相等的弦所对的弧是否相等?
预设:
图11
图12
结论:如果不在同圆或者等圆中,相等的弦所对的弧不相等,所对的圆周角也不相等.
【活动四】
1.问题:在同圆中,同一条弦所对的圆周角不一定相等,那么它们有什么关系?
分析:根据同弧所对的圆周角和圆心角之间的关系,可知:
∠C=∠2;∠D=∠1;而∠1+∠2=360°,
所以∠C+∠D=180°,即:∠C和∠D互补.
图13
2.问题:在图13中,∠CAD和∠CBD有什么数量关系?
说明:四个顶点均在同一个圆上的四边形,叫做这个圆的内接四边形.
分析:圆内接四边形ACBD的内角和是360°,∠C和∠D互补,因此,∠CAD和∠CBD也是互补的.
推论2:圆内接四边形对角互补.
【活动五】
1.问题:如图14,∠C
和∠D有可能相等吗?什么时候相等?
分析:由于∠C+∠D
=180°,要使∠C
=∠D,
那么∠C和∠D就都等于90°,需要等于,
此时的两个弧也就是半圆,因此AB就是圆的直径.
由此可得:当AB是直径即和是半圆的时候,
∠C
和∠D相等,等于90°.
图14
推论3:半圆(或直径)所对的圆周角是直角.
从圆周角定理出发进行证明:
∵AB是⊙O的直径,
∴∠AOB
=180°,
∴∠C
=∠D
=∠AOB
=90°.
说明:反之,如果∠C等于90°,也可以得到∠AOB
等于180°,从而证得AB是直径.由此我们就得到了圆周角的第4条推论.
推论4:90°的圆周角所对弦是直径.
【活动六】
如图15,A,B,C,D是⊙O上的四个点,
(1)∠1=∠
______;∠2=∠
______.
(2)若∠1=∠2,你还能从图中找出哪些相等的量?
(3)若AC是直径,∠1=∠2,那么∠3=_______°.
图15
(4)若∠1+∠2=∠BAD=90°,那么AC______BD(填“>”、“<”、“=”).
【活动七】
1.知识小结:让我们一起回顾圆周角及其四个推论的探究过程:
圆周角定理:一条弧所对圆周角等于它所对的圆心角的一半.
圆周角不唯一
归纳共性
推论1:同弧或等弧所对的圆周角相等;
(反之)在同圆或等圆中,相等的圆周角所对的弧相等.
由等弧到等弦
由此及彼
推论2:圆内接四边形对角互补.
弦变直径
一般到特殊
推论3:
半圆(或直径)所对的圆周角是直角.
交换条件和结论
逆命题
推论4:
90°的圆周角所对弦是直径.
即:圆周角的四个推论探究的就是同弧或等弧的条件下,圆周角之间、所对的弦与圆周角之间的关系.
2.方法小结:通过归纳共性、改变条件、由特殊到一般或者由一般到特殊、得到逆命题等方法提出新的问题并加以探究.
A层:
1.已知,如图16,在⊙O中,AD是直径,BC是弦,
,
由这些条件你能推出哪些结论?(至少写出4个)
图16
2.将圆周角定理及其四个推论的条件和结论整理在笔记本上.
B层:
1.整理圆周角定理及四个推论,完善圆心角、圆周角、弧、弦之间的关系结构图.
2.如图17,在△ABC中,
AB=AC,以AB为直径作⊙O,
交BC于D,
交AC于E.
试说明∠BAD和∠EDC之间的数量关系.
图17
同课章节目录
- 第十八章 相似形
- 18.1 比例线段
- 18.2 黄金分割
- 18.3 平行线分三角形两边成比例
- 18.4 相似多边形
- 18.5 相似三角形的判定
- 18.6 相似三角形的性质
- 18.7 应用举例
- 第十九章 二次函数和反比例函数
- 19.1 二次函数
- 19.2 二次函数 y=ax2+bx+c(a≠0) 的图象
- 19.3 二次函数的性质
- 19.4 二次函数的应用
- 19.5 反比例函数
- 19.6 反比例函数的图象、性质和应用
- 第二十章 解直角三角形
- 20.1 锐角三角函数
- 20.2 30°、45°、60° 角的三角函数值
- 20.3 用科学计算器求锐角三角函数值
- 20.4 解直角三角形
- 20.5 测量与计算
- 第二十一章 圆(上)
- 21.1 圆的有关概念
- 21.2 过三点的圆
- 21.3 圆的对称性
- 21.4 圆周角
- 第二十二章 圆(下)
- 22.1 直线和圆的位置关系
- 22.2 圆的切线
- 22.3 正多边形的有关计算
