人教版 九年级上册24.2.2直线和圆的位置关系复习 教学设计(表格式)
文档属性
| 名称 | 人教版 九年级上册24.2.2直线和圆的位置关系复习 教学设计(表格式) |

|
|
| 格式 | zip | ||
| 文件大小 | 209.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-20 00:00:00 | ||
图片预览


文档简介
课程基本信息
课题
24.2.2直线和圆的位置关系复习
教科书
书名:《义务教育教科书?数学(九年级上册)》
出版社:
人民教育出版社
出版日期:2019
年7
月
教学目标
教学目标:1.掌握直线和圆的三种位置关系的判定方法和性质;
2.通过分析,对比,能够综合运用圆的切线性质和判定解决问题;
3.通过对基本图形的分析,理解直线与圆的基本性质,增强学生学习的
自信心.
教学重点:直线和圆的位置关系性质与判定的综合应用.
教学难点:圆的切线性质与判定的综合应用.
教学过程
时间
教学环节
主要师生活动
3min
20min
1min
活动1
复习直线和圆的位置关系
活动2
直线与圆的位置关系的综合应用
活动3
课堂小结
课后作业
1.1直线与圆的位置关系有哪几种?它们都是如何定义的?
如果直线与圆没有公共点,那么直线与圆相离;
如果直线与圆只有一个公共点,那么直线与圆相切;
如果直线与圆有两个公共点,那么直线与圆相交.
1.2判断直线与圆位置关系的方法有哪些?
用直线与圆公共点个数进行判断(即用定义法判断);
用圆心到直线的距离d与圆的半径r之间的数量关系进行判断.
1.3判断直线与圆相切的方法有哪些?
和圆只有一个公共点的直线是圆的切线;
和圆心的距离等于半径的直线是圆的切线;
经过半径外端且垂直于半径的直线是圆的切线.
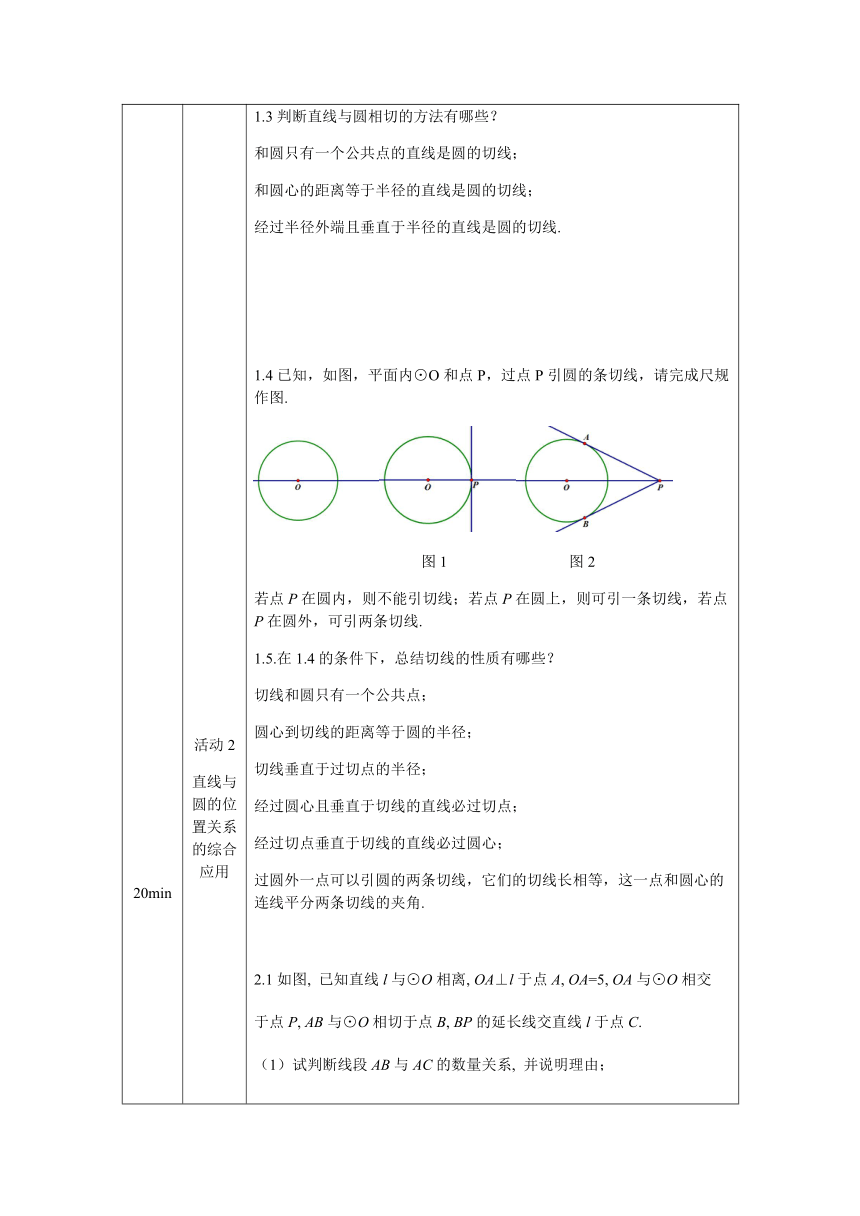
1.4已知,如图,平面内⊙O和点P,过点P引圆的条切线,请完成尺规作图.
图1
图2
若点P在圆内,则不能引切线;若点P在圆上,则可引一条切线,若点P在圆外,可引两条切线.
1.5.在1.4的条件下,总结切线的性质有哪些?
切线和圆只有一个公共点;
圆心到切线的距离等于圆的半径;
切线垂直于过切点的半径;
经过圆心且垂直于切线的直线必过切点;
经过切点垂直于切线的直线必过圆心;
过圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角.
2.1如图,
已知直线l与⊙O相离,
OA⊥l于点A,
OA=5,
OA与⊙O相交
于点P,
AB与⊙O相切于点B,
BP的延长线交直线l于点C.
(1)试判断线段AB与AC的数量关系,
并说明理由;
(2)若PC=2,
求⊙O的半径长.
归纳总结:利用直线与圆相切的位置关系解题.
基本思路:利用切线的性质构造直角三角形,借助直角三角形建立已知与未知之间的联系.
数学思想方法:转化,方程和函数思想.
数学模型:直角三角形.
2.2已知,
O为原点,
点A(4,
3),
⊙A半径为2,
过A作平行于x轴的直线l,
点P在l上运动.
(1)若点P的横坐标为12,
则判断直线OP与⊙A的位置关系.
(2)若直线OP与⊙A相切,求P点坐标.
归纳总结:判断直线与圆的位置关系,常用方法是用d与r的数量关系.
基本思路:结合直角三角形的基本图形,利用面积和勾股定理表示线段长度,布列方程.
数学思想方法:转化,方程和分类讨论思想.
数学模型:直角三角形,三角形面积表示.
课堂小结:在解决直线与圆的综合问题时
1.如果题目中给定了直线和圆的位置关系,则要充分挖掘由位置关系所产生的数量关系,用好基本图形;
2.如果题目中给定了线段及角的数量关系,则要充分挖掘由数量关系所产生的图形各元素之间的位置关系,用好基本图形;
3.学会从运动变化的角度分析问题。
1.如图,AB为O的直径,射线AP交O于C点,∠PCO的平分线交O于D点,过点D作交AP于E点.
(1)求证:DE为O的切线;
(2)若,,求直径的长.
2.在平面直角坐标系xOy中,过点作AB⊥x轴于点B.半径为
的⊙A与AB交于点C,过B点作⊙A的切线BD,切点为D,
连接DC并延长交x轴于点E.
(1)当时,EB的长等于
;
(2)点E的坐标为
(用含r的代数式表示).
课题
24.2.2直线和圆的位置关系复习
教科书
书名:《义务教育教科书?数学(九年级上册)》
出版社:
人民教育出版社
出版日期:2019
年7
月
教学目标
教学目标:1.掌握直线和圆的三种位置关系的判定方法和性质;
2.通过分析,对比,能够综合运用圆的切线性质和判定解决问题;
3.通过对基本图形的分析,理解直线与圆的基本性质,增强学生学习的
自信心.
教学重点:直线和圆的位置关系性质与判定的综合应用.
教学难点:圆的切线性质与判定的综合应用.
教学过程
时间
教学环节
主要师生活动
3min
20min
1min
活动1
复习直线和圆的位置关系
活动2
直线与圆的位置关系的综合应用
活动3
课堂小结
课后作业
1.1直线与圆的位置关系有哪几种?它们都是如何定义的?
如果直线与圆没有公共点,那么直线与圆相离;
如果直线与圆只有一个公共点,那么直线与圆相切;
如果直线与圆有两个公共点,那么直线与圆相交.
1.2判断直线与圆位置关系的方法有哪些?
用直线与圆公共点个数进行判断(即用定义法判断);
用圆心到直线的距离d与圆的半径r之间的数量关系进行判断.
1.3判断直线与圆相切的方法有哪些?
和圆只有一个公共点的直线是圆的切线;
和圆心的距离等于半径的直线是圆的切线;
经过半径外端且垂直于半径的直线是圆的切线.
1.4已知,如图,平面内⊙O和点P,过点P引圆的条切线,请完成尺规作图.
图1
图2
若点P在圆内,则不能引切线;若点P在圆上,则可引一条切线,若点P在圆外,可引两条切线.
1.5.在1.4的条件下,总结切线的性质有哪些?
切线和圆只有一个公共点;
圆心到切线的距离等于圆的半径;
切线垂直于过切点的半径;
经过圆心且垂直于切线的直线必过切点;
经过切点垂直于切线的直线必过圆心;
过圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角.
2.1如图,
已知直线l与⊙O相离,
OA⊥l于点A,
OA=5,
OA与⊙O相交
于点P,
AB与⊙O相切于点B,
BP的延长线交直线l于点C.
(1)试判断线段AB与AC的数量关系,
并说明理由;
(2)若PC=2,
求⊙O的半径长.
归纳总结:利用直线与圆相切的位置关系解题.
基本思路:利用切线的性质构造直角三角形,借助直角三角形建立已知与未知之间的联系.
数学思想方法:转化,方程和函数思想.
数学模型:直角三角形.
2.2已知,
O为原点,
点A(4,
3),
⊙A半径为2,
过A作平行于x轴的直线l,
点P在l上运动.
(1)若点P的横坐标为12,
则判断直线OP与⊙A的位置关系.
(2)若直线OP与⊙A相切,求P点坐标.
归纳总结:判断直线与圆的位置关系,常用方法是用d与r的数量关系.
基本思路:结合直角三角形的基本图形,利用面积和勾股定理表示线段长度,布列方程.
数学思想方法:转化,方程和分类讨论思想.
数学模型:直角三角形,三角形面积表示.
课堂小结:在解决直线与圆的综合问题时
1.如果题目中给定了直线和圆的位置关系,则要充分挖掘由位置关系所产生的数量关系,用好基本图形;
2.如果题目中给定了线段及角的数量关系,则要充分挖掘由数量关系所产生的图形各元素之间的位置关系,用好基本图形;
3.学会从运动变化的角度分析问题。
1.如图,AB为O的直径,射线AP交O于C点,∠PCO的平分线交O于D点,过点D作交AP于E点.
(1)求证:DE为O的切线;
(2)若,,求直径的长.
2.在平面直角坐标系xOy中,过点作AB⊥x轴于点B.半径为
的⊙A与AB交于点C,过B点作⊙A的切线BD,切点为D,
连接DC并延长交x轴于点E.
(1)当时,EB的长等于
;
(2)点E的坐标为
(用含r的代数式表示).
同课章节目录
