人教版九年级上册23.2.3关于原点对称的点的坐标 教学设计(表格式)
文档属性
| 名称 | 人教版九年级上册23.2.3关于原点对称的点的坐标 教学设计(表格式) |

|
|
| 格式 | zip | ||
| 文件大小 | 93.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-20 00:00:00 | ||
图片预览

文档简介
课程基本信息
课题
23.
2.
3
关于原点对称的点的坐标
教科书
书名:《义务教育教科书
数学(九年级上册)》
出版社:
人民教育出版社
出版日期:2014年3月
教学目标
教学目标:了解关于原点对称的点的坐标之间的关系;
教学重点:两个点关于原点对称时,
它们坐标之间的关系.
教学难点:运用关于原点对称的点的坐标之间的关系解决问题.
教学过程
时间
教学环节
主要师生活动
2min
复习回顾
复习如何画出一个点关于另一个点的对称点
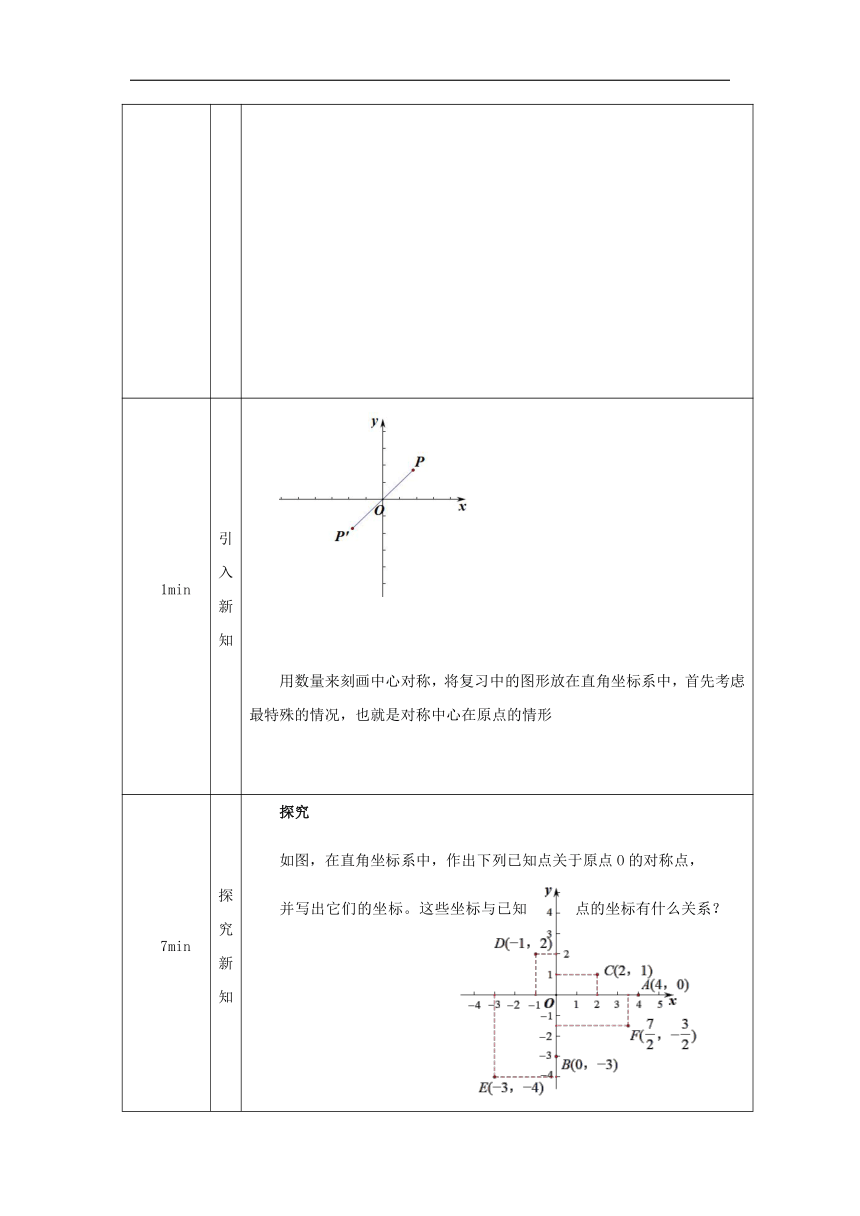
如图,画出点P关于点O的对称点。
1min
引入新知
用数量来刻画中心对称,将复习中的图形放在直角坐标系中,首先考虑最特殊的情况,也就是对称中心在原点的情形
7min
探究新知
探究
如图,在直角坐标系中,作出下列已知点关于原点O的对称点,
并写出它们的坐标。这些坐标与已知点的坐标有什么关系?
通过6个特殊点归纳出关于原点对称的点的坐标关系,然后利用全等三角形证明,最终得出结论:两个点关于原点对称时,它们的坐标符号相反,即点关于原点的对称点为
10min
例题解析
例1
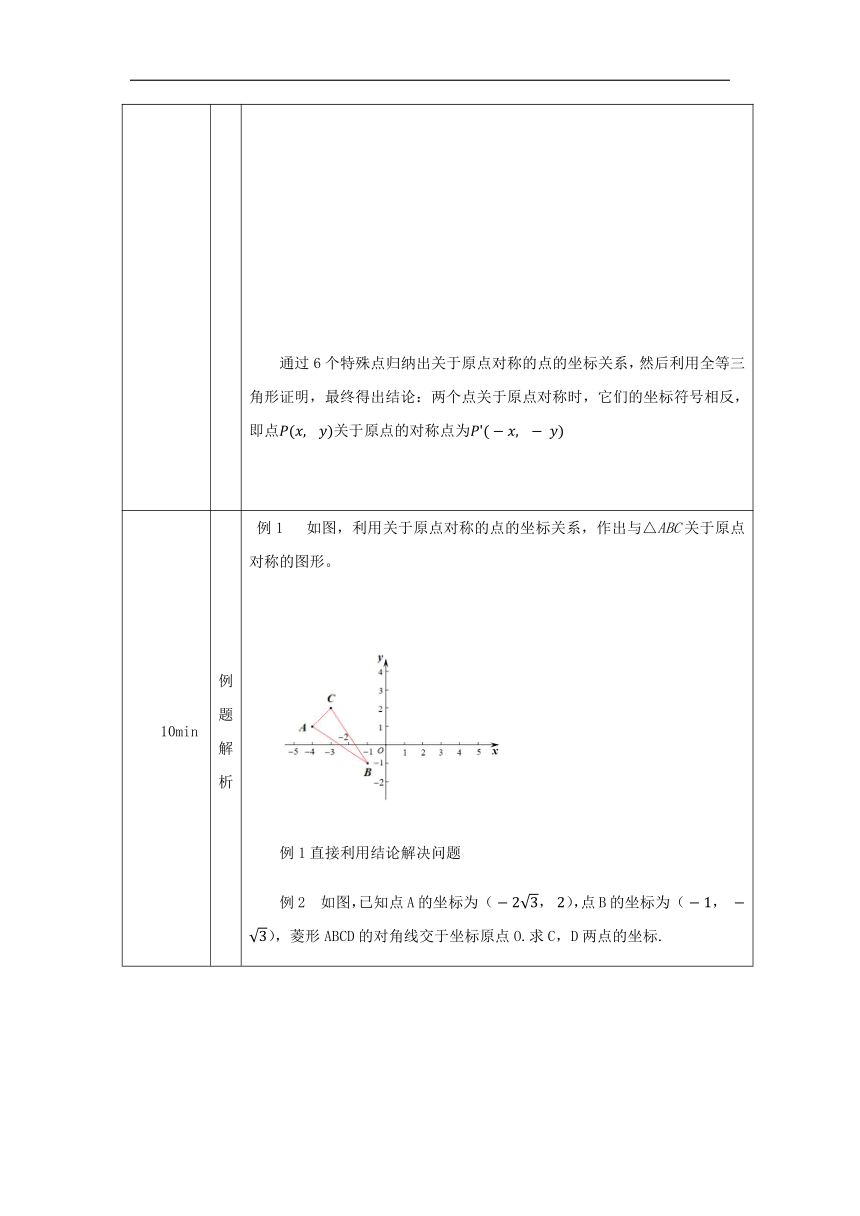
如图,利用关于原点对称的点的坐标关系,作出与△ABC关于原点对称的图形。
例1直接利用结论解决问题
例2
如图,已知点A的坐标为,点B的坐标为,菱形ABCD的对角线交于坐标原点O.求C,D两点的坐标.
例3
已知点原点的对称点在第一象限,求整数的值。
例2和例3是教材上的配套练习题,例2用到菱形的性质,例3要用到不等式的知识。
例4
如图,点关于点
的对称点为点。求证:
例4研究对称中心为一般点的情况,引导学生转化为对称中心在原点的情况,进而得到一般的结论。
例5
如图,利用例4所得的结论,作出△ABC关于点对称的图形。
例5是在例4的基础上解决问题,利用例4的结论可以求出一般情况下中心对称的点的坐标关系。
例6
已知直线画出直线关于原点O对称的直线,并求出直线的解析式.
由点到线,探求直线关于原点对称后解析式的求法,也为抛物线关于原点对称之后解析式的求法提供了思路
1min
课堂小结
两个点关于原点对称时,它们的坐标符号相反,坐标的绝对值相等,即点关于原点的对称点为
1min
布置作业
请同学们在作业本上完成下面三道课后作业:
下列各点中哪两个点关于原点O对称?
,,,,,,.
(1)
写出下列各点关于原点的对称点,,,的坐标:
,,,.
(2)
写出下列各点关于P(1,2)的对称点,,,的坐标:
,,,.
已知抛物线的解析式为
,画出这条抛物线,并求出它关于原点对称所得的抛物线的解析式.
课题
23.
2.
3
关于原点对称的点的坐标
教科书
书名:《义务教育教科书
数学(九年级上册)》
出版社:
人民教育出版社
出版日期:2014年3月
教学目标
教学目标:了解关于原点对称的点的坐标之间的关系;
教学重点:两个点关于原点对称时,
它们坐标之间的关系.
教学难点:运用关于原点对称的点的坐标之间的关系解决问题.
教学过程
时间
教学环节
主要师生活动
2min
复习回顾
复习如何画出一个点关于另一个点的对称点
如图,画出点P关于点O的对称点。
1min
引入新知
用数量来刻画中心对称,将复习中的图形放在直角坐标系中,首先考虑最特殊的情况,也就是对称中心在原点的情形
7min
探究新知
探究
如图,在直角坐标系中,作出下列已知点关于原点O的对称点,
并写出它们的坐标。这些坐标与已知点的坐标有什么关系?
通过6个特殊点归纳出关于原点对称的点的坐标关系,然后利用全等三角形证明,最终得出结论:两个点关于原点对称时,它们的坐标符号相反,即点关于原点的对称点为
10min
例题解析
例1
如图,利用关于原点对称的点的坐标关系,作出与△ABC关于原点对称的图形。
例1直接利用结论解决问题
例2
如图,已知点A的坐标为,点B的坐标为,菱形ABCD的对角线交于坐标原点O.求C,D两点的坐标.
例3
已知点原点的对称点在第一象限,求整数的值。
例2和例3是教材上的配套练习题,例2用到菱形的性质,例3要用到不等式的知识。
例4
如图,点关于点
的对称点为点。求证:
例4研究对称中心为一般点的情况,引导学生转化为对称中心在原点的情况,进而得到一般的结论。
例5
如图,利用例4所得的结论,作出△ABC关于点对称的图形。
例5是在例4的基础上解决问题,利用例4的结论可以求出一般情况下中心对称的点的坐标关系。
例6
已知直线画出直线关于原点O对称的直线,并求出直线的解析式.
由点到线,探求直线关于原点对称后解析式的求法,也为抛物线关于原点对称之后解析式的求法提供了思路
1min
课堂小结
两个点关于原点对称时,它们的坐标符号相反,坐标的绝对值相等,即点关于原点的对称点为
1min
布置作业
请同学们在作业本上完成下面三道课后作业:
下列各点中哪两个点关于原点O对称?
,,,,,,.
(1)
写出下列各点关于原点的对称点,,,的坐标:
,,,.
(2)
写出下列各点关于P(1,2)的对称点,,,的坐标:
,,,.
已知抛物线的解析式为
,画出这条抛物线,并求出它关于原点对称所得的抛物线的解析式.
同课章节目录
