_人教版九年级上册24.1.4圆周角(1) 教学设计(表格式)
文档属性
| 名称 | _人教版九年级上册24.1.4圆周角(1) 教学设计(表格式) |

|
|
| 格式 | zip | ||
| 文件大小 | 314.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-20 00:00:00 | ||
图片预览

文档简介
教学设计
课程基本信息
课题
24.1.4圆周角(1)
教科书
书名:《义务教育教科书
数学(九年级上册)》
出版社:
人民教育出版社
出版日期:
2014
年
3
月
教学目标
教学目标:
1.理解圆周角的概念,了解并证明圆周角定理及其推论;
2.准确地运用圆周角定理及其推论进行简单的证明计算;
3.通过观察、比较、分析圆周角与圆心角的关系发展学生合情推理和演绎推理的能力;
4.经历探究同弧或等弧所对圆周角与圆心角的关系的过程,进一步体会分类讨论、转化、归纳的思想方法;
5.经过探索圆周角定理的过程,发展学生的数学思考能力.
教学重点:圆周角定理及其推导;
教学难点:圆周角定理的证明中的分类讨论.
教学过程
时间
教学环节
主要师生活动
课程引入
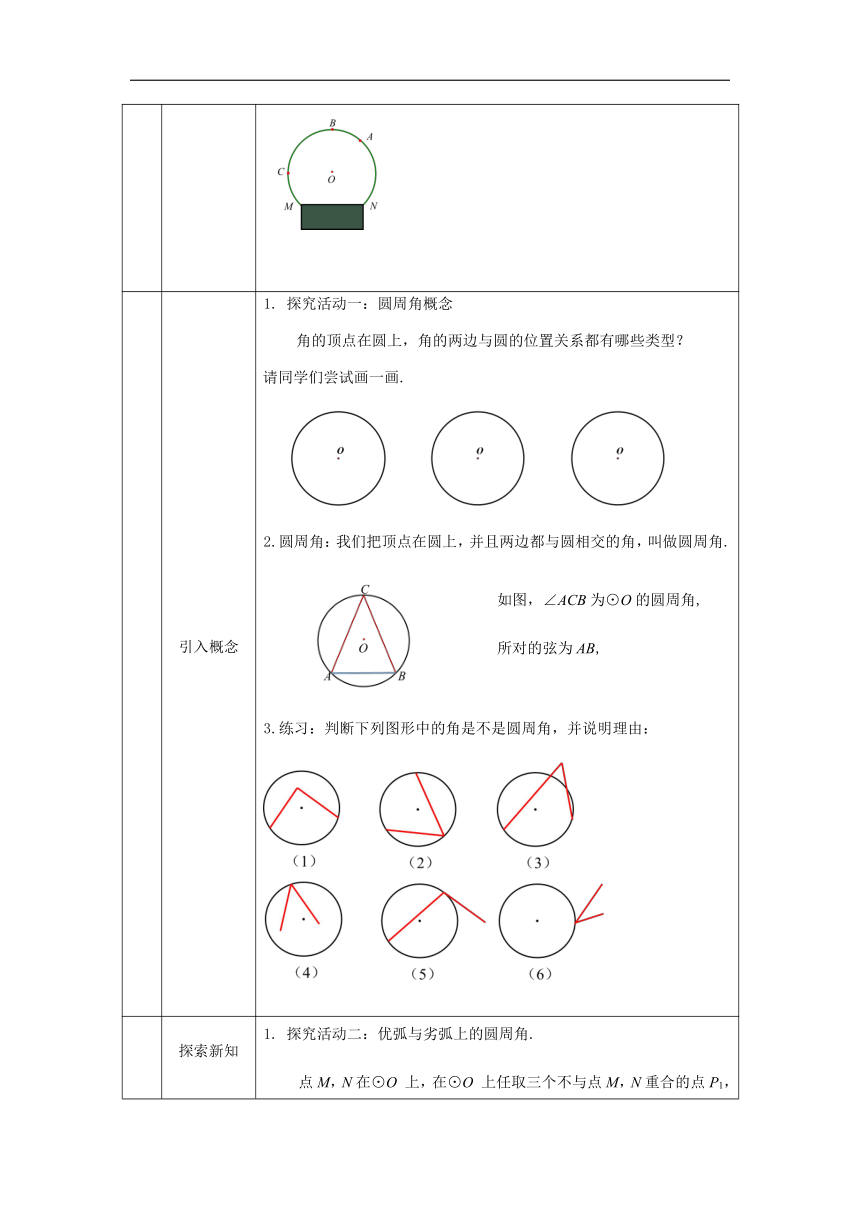
如图:教练让甲,
乙,
丙三人分别在A,
B,
C三处射门,仅从射门角度大小考虑,教练的做法公平吗?为什么?
引入概念
1.
探究活动一:圆周角概念
角的顶点在圆上,角的两边与圆的位置关系都有哪些类型?
请同学们尝试画一画.
2.圆周角:我们把顶点在圆上,并且两边都与圆相交的角,叫做圆周角.
3.练习:判断下列图形中的角是不是圆周角,并说明理由:
探索新知
1.
探究活动二:优弧与劣弧上的圆周角.
点M,N在⊙O
上,在⊙O
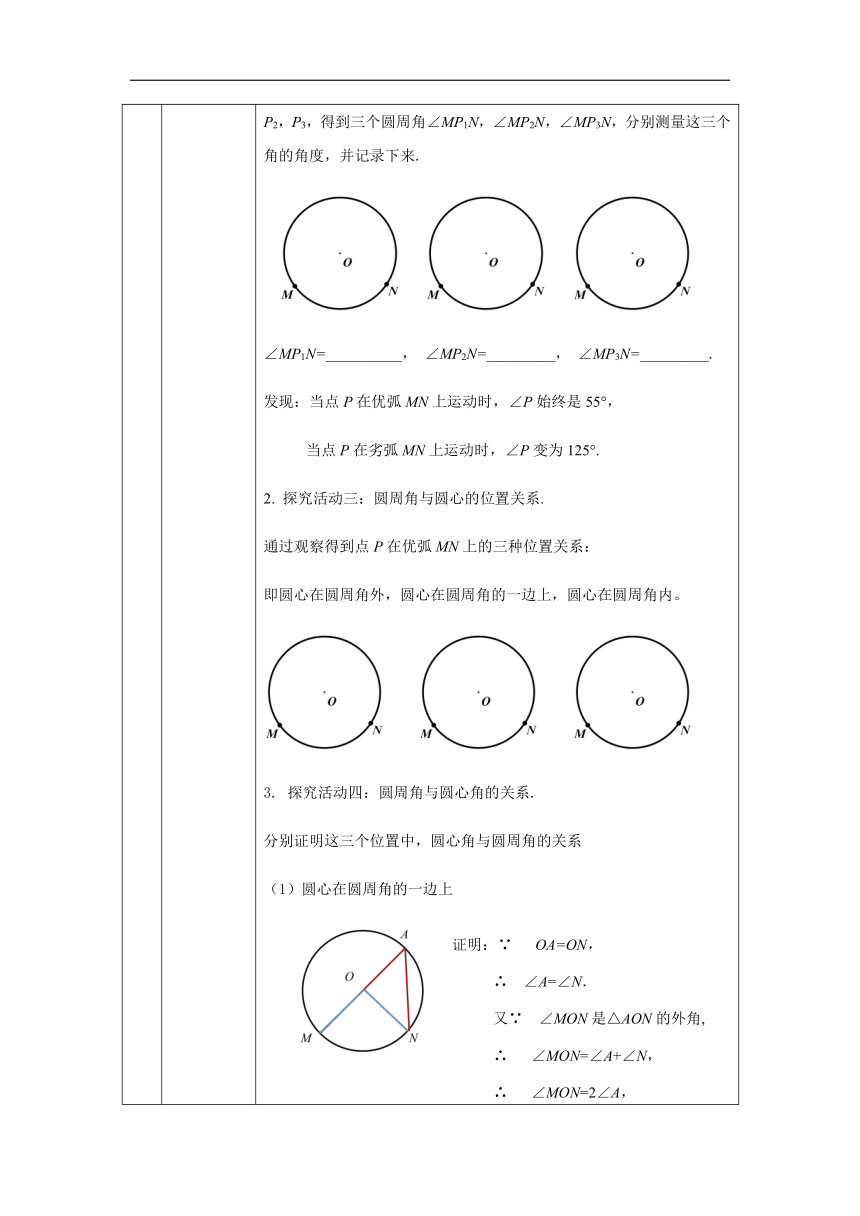
上任取三个不与点M,N重合的点P1,P2,P3,得到三个圆周角∠MP1N,∠MP2N,∠MP3N,分别测量这三个角的角度,并记录下来.
∠MP1N=__________,
∠MP2N=_________,
∠MP3N=_________.
发现:当点P在优弧MN上运动时,∠P始终是55°,
当点P在劣弧MN上运动时,∠P变为125°.
2.
探究活动三:圆周角与圆心的位置关系.
通过观察得到点P在优弧MN上的三种位置关系:
即圆心在圆周角外,圆心在圆周角的一边上,圆心在圆周角内。
3.
探究活动四:圆周角与圆心角的关系.
分别证明这三个位置中,圆心角与圆周角的关系
(1)圆心在圆周角的一边上
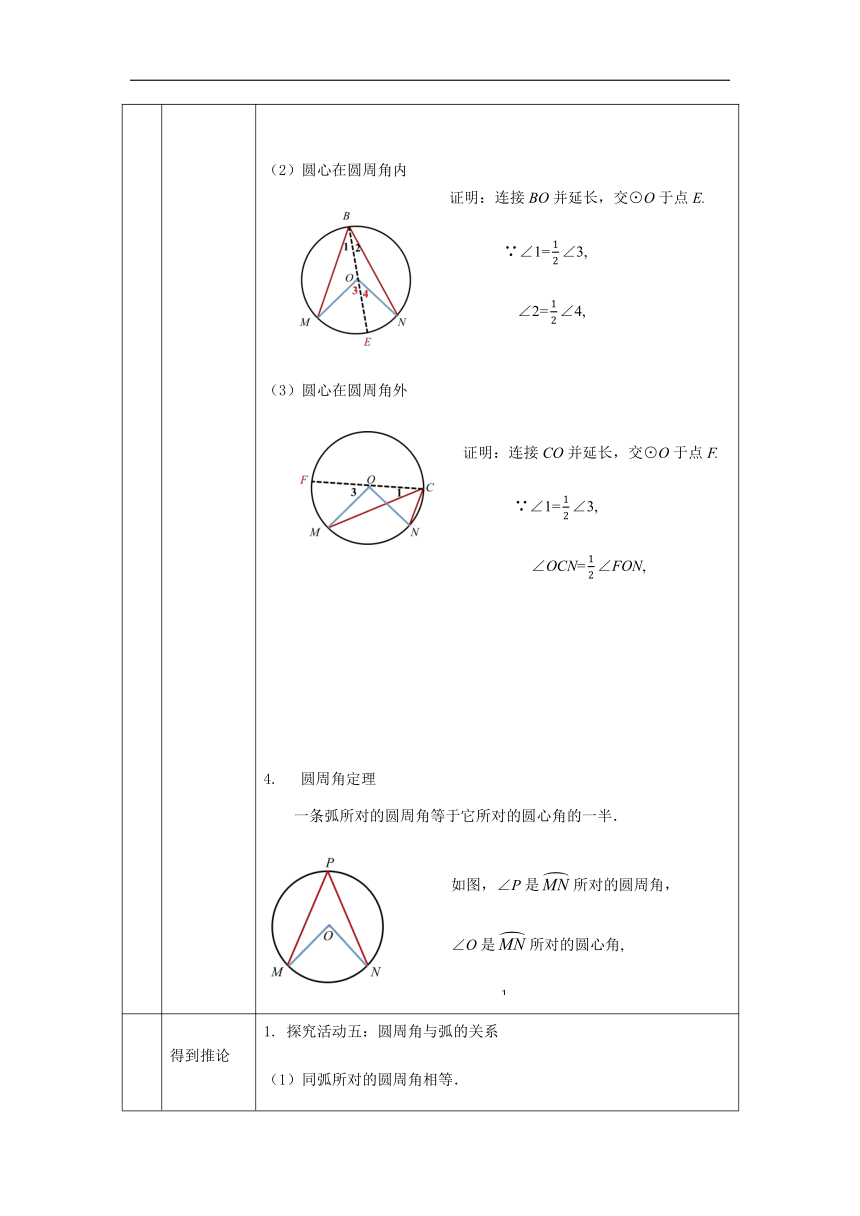
(2)圆心在圆周角内
(3)圆心在圆周角外
4.
圆周角定理
一条弧所对的圆周角等于它所对的圆心角的一半.
得到推论
1.
探究活动五:圆周角与弧的关系
(1)同弧所对的圆周角相等.
如图,∠P,∠Q是所对的圆周角,
2.等弧所对的圆周角相等.
已知:如图,与相等,求证:
3.
圆周角定理推论(一)
同弧或等弧所对的圆周角相等.
由一般
到特殊
1.探究活动六:特殊的角度
在左图⊙O上画出直径MN,及其所对的圆周角∠MPN,并测量∠MPN的角度.
在右图⊙O上画出个以点P为顶点的圆周角∠MPN,使∠MPN=90°,再画出它所对的圆心角∠MON,并测量∠MON的角度.
发现:
当∠O变为180°,即MN是圆O直径时,∠P=90°,
反之,圆周角∠P为90°时,圆心角∠O则为180°.
2.圆周角定理推论(二)
半圆(或直径)所对的圆周角是直角.
90°的圆周角所对的弦是直径.
3.练习
1.如图①,已知AB是⊙O的直径,点C在⊙O上,若∠CAB=40°,
则∠ABC=_______°.
2.如图②,△ABC的顶点都在⊙O上,BD是⊙O直径,若∠CBD=21°,则∠A=_______°.
例题分析
例:如图,⊙O
的直径
AB
为
10
cm,弦
AC
为
6
cm,∠ACB
的平分线交⊙O
于点
D,求
BC,AD,BD
的长.
课堂小结
1.圆周角、圆心角与弧之间的关系
2.直径与直角之间的关系
课后作业
1.如图,OA,OB,OC都是⊙O
的半径,∠AOB=2∠BOC.
求证:∠ACB=2∠BAC.
2.如图,你能用三角尺确定一张圆形纸片的圆心吗?有几种方法?与同学交流一下.
提高作业
提高题:如图,圆上分布着7个点,A1,A2,……,A7,从A1起顺次连接A3,A5,A7,A2,A4,A6,A1,得到“七角星”,则∠A1+∠A2+……+∠A7=_______
课程基本信息
课题
24.1.4圆周角(1)
教科书
书名:《义务教育教科书
数学(九年级上册)》
出版社:
人民教育出版社
出版日期:
2014
年
3
月
教学目标
教学目标:
1.理解圆周角的概念,了解并证明圆周角定理及其推论;
2.准确地运用圆周角定理及其推论进行简单的证明计算;
3.通过观察、比较、分析圆周角与圆心角的关系发展学生合情推理和演绎推理的能力;
4.经历探究同弧或等弧所对圆周角与圆心角的关系的过程,进一步体会分类讨论、转化、归纳的思想方法;
5.经过探索圆周角定理的过程,发展学生的数学思考能力.
教学重点:圆周角定理及其推导;
教学难点:圆周角定理的证明中的分类讨论.
教学过程
时间
教学环节
主要师生活动
课程引入
如图:教练让甲,
乙,
丙三人分别在A,
B,
C三处射门,仅从射门角度大小考虑,教练的做法公平吗?为什么?
引入概念
1.
探究活动一:圆周角概念
角的顶点在圆上,角的两边与圆的位置关系都有哪些类型?
请同学们尝试画一画.
2.圆周角:我们把顶点在圆上,并且两边都与圆相交的角,叫做圆周角.
3.练习:判断下列图形中的角是不是圆周角,并说明理由:
探索新知
1.
探究活动二:优弧与劣弧上的圆周角.
点M,N在⊙O
上,在⊙O
上任取三个不与点M,N重合的点P1,P2,P3,得到三个圆周角∠MP1N,∠MP2N,∠MP3N,分别测量这三个角的角度,并记录下来.
∠MP1N=__________,
∠MP2N=_________,
∠MP3N=_________.
发现:当点P在优弧MN上运动时,∠P始终是55°,
当点P在劣弧MN上运动时,∠P变为125°.
2.
探究活动三:圆周角与圆心的位置关系.
通过观察得到点P在优弧MN上的三种位置关系:
即圆心在圆周角外,圆心在圆周角的一边上,圆心在圆周角内。
3.
探究活动四:圆周角与圆心角的关系.
分别证明这三个位置中,圆心角与圆周角的关系
(1)圆心在圆周角的一边上
(2)圆心在圆周角内
(3)圆心在圆周角外
4.
圆周角定理
一条弧所对的圆周角等于它所对的圆心角的一半.
得到推论
1.
探究活动五:圆周角与弧的关系
(1)同弧所对的圆周角相等.
如图,∠P,∠Q是所对的圆周角,
2.等弧所对的圆周角相等.
已知:如图,与相等,求证:
3.
圆周角定理推论(一)
同弧或等弧所对的圆周角相等.
由一般
到特殊
1.探究活动六:特殊的角度
在左图⊙O上画出直径MN,及其所对的圆周角∠MPN,并测量∠MPN的角度.
在右图⊙O上画出个以点P为顶点的圆周角∠MPN,使∠MPN=90°,再画出它所对的圆心角∠MON,并测量∠MON的角度.
发现:
当∠O变为180°,即MN是圆O直径时,∠P=90°,
反之,圆周角∠P为90°时,圆心角∠O则为180°.
2.圆周角定理推论(二)
半圆(或直径)所对的圆周角是直角.
90°的圆周角所对的弦是直径.
3.练习
1.如图①,已知AB是⊙O的直径,点C在⊙O上,若∠CAB=40°,
则∠ABC=_______°.
2.如图②,△ABC的顶点都在⊙O上,BD是⊙O直径,若∠CBD=21°,则∠A=_______°.
例题分析
例:如图,⊙O
的直径
AB
为
10
cm,弦
AC
为
6
cm,∠ACB
的平分线交⊙O
于点
D,求
BC,AD,BD
的长.
课堂小结
1.圆周角、圆心角与弧之间的关系
2.直径与直角之间的关系
课后作业
1.如图,OA,OB,OC都是⊙O
的半径,∠AOB=2∠BOC.
求证:∠ACB=2∠BAC.
2.如图,你能用三角尺确定一张圆形纸片的圆心吗?有几种方法?与同学交流一下.
提高作业
提高题:如图,圆上分布着7个点,A1,A2,……,A7,从A1起顺次连接A3,A5,A7,A2,A4,A6,A1,得到“七角星”,则∠A1+∠A2+……+∠A7=_______
同课章节目录
