沪科版九年级数学下册第24章圆章末复习作业试卷(word解析版)
文档属性
| 名称 | 沪科版九年级数学下册第24章圆章末复习作业试卷(word解析版) |
|
|
| 格式 | zip | ||
| 文件大小 | 356.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-20 00:00:00 | ||
图片预览

文档简介
沪科版九年级数学下第24章 圆章末复习作业
一、选择题
1.
下列图形既是轴对称图形又是中心对称图形的是
( )
图1
2.
如图2,在平面直角坐标系中,将点P(2,3)绕原点O顺时针旋转90°得到点P',则点P'的坐标为
( )
图2
A.(3,2)
B.(3,-1)
C.(2,-3)
D.(3,-2)
3.
如图3,四边形ABCD内接于☉O,连接BD.若=,∠BDC=50°,则∠ADC的度数是
( )
图3
A.125°
B.130°
C.135°
D.140°
4.
如图4,点A,B,C在☉O上,∠ACB=54°,则∠ABO的度数是
( )
图4
A.54°
B.27°
C.36°
D.108°
5.
如图5,在6×6的正方形网格中,每个小正方形的边长都是1,点A,B,C均在网格线的交点上,☉O是△ABC的外接圆,则cos∠BAC的值为
( )
图5
A.
B.
C.
D.
6.
如图6,AD是☉O的直径,BC是弦,四边形OBCD是平行四边形,AC与OB相交于点P,下列结论错误的是
( )
图6
A.AP=2OP
B.CD=2OP
C.OB⊥AC
D.AC平分OB
7.
如图7,半径为3的☉A经过原点O和点C(0,2),B是y轴左侧☉A优弧上一点,则tan∠OBC的值为
( )
图7
A.
B.2
C.
D.
8.
如图8,在正六边形ABCDEF中,AC=2,则正六边形ABCDEF的边长是
( )
图8
A.1
B.
C.
D.2
9.
如图9,有一块半径为1
m,圆心角为90°的扇形铁皮,要把它做成一个圆锥形容器的侧面(接缝忽略不计),那么这个圆锥形容器的高为
( )
图9
A.
m
B.
m
C.
m
D.
m
10.
如图10,☉O是等边三角形ABC的内切圆,分别切AB,BC,AC于点E,F,D,P是上一点,则∠EPF的度数是
( )
图10
A.65°
B.60°
C.58°
D.50°
二、填空题
11.
如图11,点A,B,C在☉O上,BC=6,∠BAC=30°,则☉O的半径为 .?
图11
12.
如图12,已知AB是☉O的直径,AC是☉O的切线,连接OC交☉O于点D,连接BD.若∠C=40°,则∠B的度数是 .?
图12
13.
直角三角形的两条直角边长分别是5和12,则它的内切圆半径为 .?
14.
用一个圆心角为120°的扇形作一个圆锥的侧面,若这个圆锥的底面半径恰好等于4,则这个圆锥的母线长为 .?
15.
如图13,AC是☉O的弦,AC=5,B是☉O上的一个动点,且∠ABC=45°,若M,N分别是AC,BC的中点,则MN的最大值是 .?
图13
三、解答题
16.
如图14,点O是半圆圆心,BE是半圆的直径,点A,D在半圆上,且AD∥BO,∠ABO=60°,AB=8,过点D作DC⊥BE于点C,求阴影部分的面积.
图14
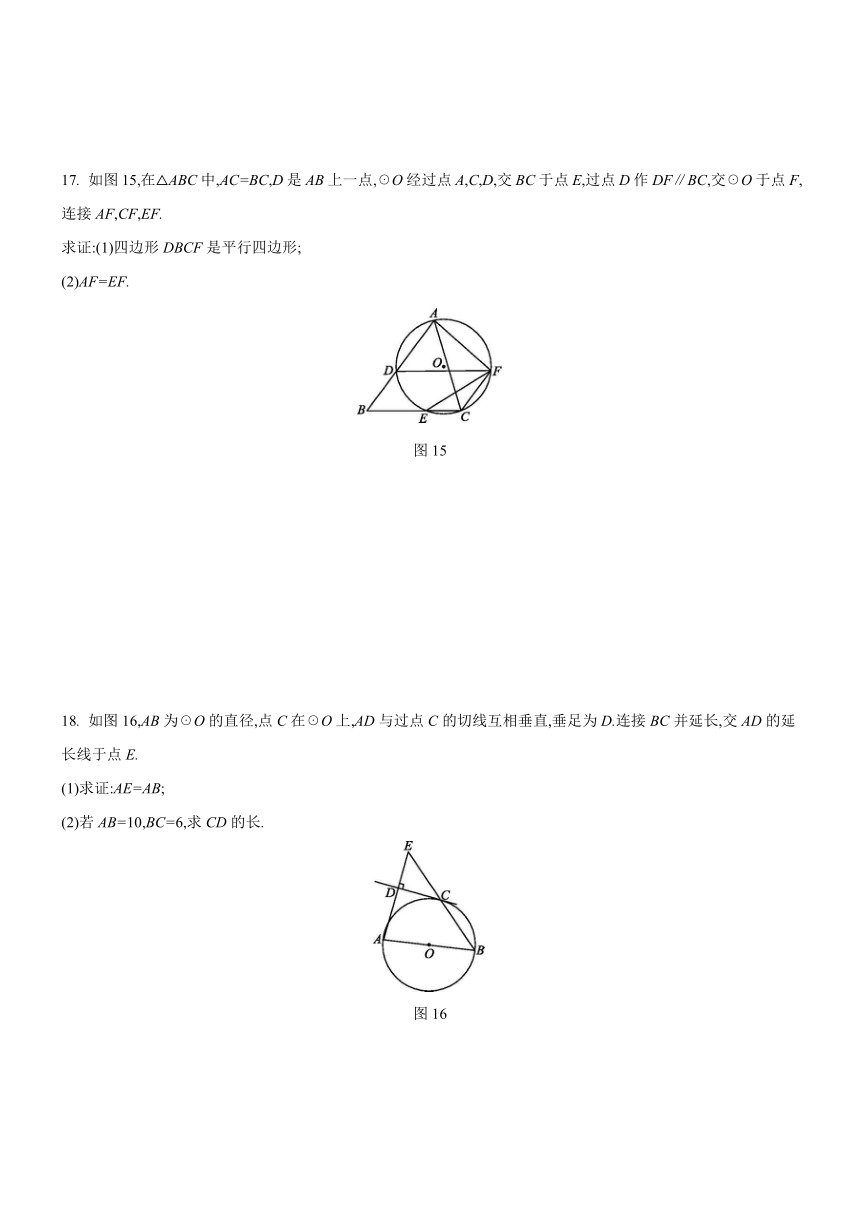
17.
如图15,在△ABC中,AC=BC,D是AB上一点,☉O经过点A,C,D,交BC于点E,过点D作DF∥BC,交☉O于点F,连接AF,CF,EF.
求证:(1)四边形DBCF是平行四边形;
(2)AF=EF.
图15
18.
如图16,AB为☉O的直径,点C在☉O上,AD与过点C的切线互相垂直,垂足为D.连接BC并延长,交AD的延长线于点E.
(1)求证:AE=AB;
(2)若AB=10,BC=6,求CD的长.
图16
参考答案
1.[答案]
B
2.[解析]
D 如图,过点P作PQ⊥y轴于点Q.
∵点P的坐标为(2,3),
∴PQ=2,OQ=3.
∵点P(2,3)绕原点O顺时针旋转90°得到点P',即把△OPQ绕原点O顺时针旋转90°得到△OP'Q',
∴∠P'Q'O=90°,P'Q'=PQ=2,OQ'=OQ=3,
∴点P'的坐标为(3,-2).故选D.
3.[解析]
B ∵=,∴∠BDC=∠ABC=50°,∴∠ADC=180°-∠ABC=130°.故选B.
4.[解析]
C ∵∠ACB=54°,
∴∠AOB=2∠ACB=108°.
∵OB=OA,∴∠ABO=∠BAO=×(180°-∠AOB)=36°.故选C.
5.[解析]
B 如图,作直径BD,连接CD.
由勾股定理,得BD==2.
在Rt△BDC中,cos∠BDC===.
由圆周角定理,得∠BAC=∠BDC,
∴cos∠BAC=cos∠BDC=.故选B.
6.[解析]
A ∵AD为☉O的直径,∴∠ACD=90°.
∵四边形OBCD为平行四边形,
∴CD∥OB,CD=OB,∴CD=OD=AD.
∵OP∥CD,CD⊥AC,
∴OP⊥AC,C选项正确;∴AP=CP.
在Rt△ACD中,sinA==,
∴∠A=30°.
在Rt△AOP中,AP=OP,∴A选项错误;
∵AP=CP,AO=DO,
∴OP为△ACD的中位线,
∴CD=2OP,∴B选项正确;∴OB=2OP,
从而AC平分OB,∴D选项正确.故选A.
7.[解析]
D 如图,作直径CD.
在Rt△OCD中,CD=6,OC=2,
则OD==4,
∴tan∠CDO==.
由圆周角定理,得∠OBC=∠CDO,
则tan∠OBC=.故选D.
8.[解析]
D 如图,过点B作BG⊥AC于点G.
∵BA=BC,BG⊥AC,
∴AG=AC=,∠BAC=∠BCA.
正六边形ABCDEF中,每个内角为(6-2)×180°÷6=120°,
∴∠ABC=120°,∴∠BAC=∠BCA=30°.
在Rt△ABG中,GB=AG·tan∠BAC=×=1,∴AB=2GB=2.即正六边形ABCDEF的边长为2.
故选D.
9.[解析]
C 先利用弧长公式求得圆锥形容器的底面半径,再利用勾股定理求圆锥的高.设圆锥形容器的底面半径为r
m,则有2πr=,解得r=,则圆锥形容器的高为=(m).
10.[解析]
B 如图,连接OE,OF.∵☉O是△ABC的内切圆,E,F是切点,∴OE⊥AB,OF⊥BC,
∴∠OEB=∠OFB=90°.
∵△ABC是等边三角形,∴∠B=60°,
∴∠EOF=120°,∴∠EPF=∠EOF=60°.故选B.
11.[答案]
6
[解析]
如图,连接OB,OC.
∵∠BOC=2∠BAC=60°,又OB=OC,
∴△BOC是等边三角形,∴OB=BC=6.
故答案为6.
12.[答案]
25°
[解析]
∵AC是☉O的切线,
∴OA⊥AC,∴∠OAC=90°,
∴∠AOC=90°-∠C=90°-40°=50°,
∴∠B=∠AOC=25°.
故答案为25°.
13.[答案]
2
[解析]
直角三角形的斜边长==13,
所以它的内切圆半径==2.
故答案为2.
14.[答案]
12
[解析]
设圆锥的母线长为l.
根据题意,得=2π×4,
解得l=12.
故答案为12.
15.[答案]
[解析]
∵M,N分别是AC,BC的中点,
∴MN=AB,
∴当AB取得最大值时,MN就取得最大值,
∴当AB是直径时,MN最大.
如图,连接AO并延长交☉O于点B',连接CB'.
∵AB'是☉O的直径,
∴∠ACB'=90°.
∵∠ABC=45°,
∴∠AB'C=45°,
∴AB'===5,
∴MN最大=.
故答案为.
16.解:如图,连接OA.∵∠ABO=60°,OA=OB,∴△AOB是等边三角形.
∵AB=8,∴☉O的半径为8.
∵AD∥BO,∴∠DAO=∠AOB=60°.
又∵OA=OD,
∴△OAD是等边三角形,∴∠AOD=60°.
∵∠AOB=∠AOD=60°,∴∠DOE=60°.
∵DC⊥BE于点C,
∴CD=OD=4,OC=OD=4,
∴BC=8+4=12,
∴S阴影=S△AOB+S扇形AOD+S扇形DOE-S△BCD=×8×4+2×-×12×4=-8.
17.证明:(1)∵AC=BC,∴∠BAC=∠B.
∵DF∥BC,∴∠ADF=∠B.
又∵∠BAC=∠CFD,∴∠ADF=∠CFD,
∴BD∥CF.
又∵DF∥BC,
∴四边形DBCF是平行四边形.
(2)如图,连接AE.
∵∠ADF=∠B,∠ADF=∠AEF,
∴∠AEF=∠B.
∵四边形AECF是☉O的内接四边形,
∴∠ECF+∠EAF=180°.
∵BD∥CF,∴∠ECF+∠B=180°,
∴∠EAF=∠B,∴∠AEF=∠EAF,
∴AF=EF.
18.解:(1)证明:如图,连接OC.∵CD为切线,∴OC⊥CD.
又∵CD⊥AD,∴OC∥AD,
∴∠OCB=∠E.
∵OB=OC,
∴∠OCB=∠B,
∴∠B=∠E,∴AE=AB.
(2)如图,连接AC.∵AB为直径,∴∠ACB=90°,
∴AC==8.
∵AB=AE=10,AC⊥BE,
∴CE=BC=6.
∵CD·AE=AC·CE,
∴CD==.
一、选择题
1.
下列图形既是轴对称图形又是中心对称图形的是
( )
图1
2.
如图2,在平面直角坐标系中,将点P(2,3)绕原点O顺时针旋转90°得到点P',则点P'的坐标为
( )
图2
A.(3,2)
B.(3,-1)
C.(2,-3)
D.(3,-2)
3.
如图3,四边形ABCD内接于☉O,连接BD.若=,∠BDC=50°,则∠ADC的度数是
( )
图3
A.125°
B.130°
C.135°
D.140°
4.
如图4,点A,B,C在☉O上,∠ACB=54°,则∠ABO的度数是
( )
图4
A.54°
B.27°
C.36°
D.108°
5.
如图5,在6×6的正方形网格中,每个小正方形的边长都是1,点A,B,C均在网格线的交点上,☉O是△ABC的外接圆,则cos∠BAC的值为
( )
图5
A.
B.
C.
D.
6.
如图6,AD是☉O的直径,BC是弦,四边形OBCD是平行四边形,AC与OB相交于点P,下列结论错误的是
( )
图6
A.AP=2OP
B.CD=2OP
C.OB⊥AC
D.AC平分OB
7.
如图7,半径为3的☉A经过原点O和点C(0,2),B是y轴左侧☉A优弧上一点,则tan∠OBC的值为
( )
图7
A.
B.2
C.
D.
8.
如图8,在正六边形ABCDEF中,AC=2,则正六边形ABCDEF的边长是
( )
图8
A.1
B.
C.
D.2
9.
如图9,有一块半径为1
m,圆心角为90°的扇形铁皮,要把它做成一个圆锥形容器的侧面(接缝忽略不计),那么这个圆锥形容器的高为
( )
图9
A.
m
B.
m
C.
m
D.
m
10.
如图10,☉O是等边三角形ABC的内切圆,分别切AB,BC,AC于点E,F,D,P是上一点,则∠EPF的度数是
( )
图10
A.65°
B.60°
C.58°
D.50°
二、填空题
11.
如图11,点A,B,C在☉O上,BC=6,∠BAC=30°,则☉O的半径为 .?
图11
12.
如图12,已知AB是☉O的直径,AC是☉O的切线,连接OC交☉O于点D,连接BD.若∠C=40°,则∠B的度数是 .?
图12
13.
直角三角形的两条直角边长分别是5和12,则它的内切圆半径为 .?
14.
用一个圆心角为120°的扇形作一个圆锥的侧面,若这个圆锥的底面半径恰好等于4,则这个圆锥的母线长为 .?
15.
如图13,AC是☉O的弦,AC=5,B是☉O上的一个动点,且∠ABC=45°,若M,N分别是AC,BC的中点,则MN的最大值是 .?
图13
三、解答题
16.
如图14,点O是半圆圆心,BE是半圆的直径,点A,D在半圆上,且AD∥BO,∠ABO=60°,AB=8,过点D作DC⊥BE于点C,求阴影部分的面积.
图14
17.
如图15,在△ABC中,AC=BC,D是AB上一点,☉O经过点A,C,D,交BC于点E,过点D作DF∥BC,交☉O于点F,连接AF,CF,EF.
求证:(1)四边形DBCF是平行四边形;
(2)AF=EF.
图15
18.
如图16,AB为☉O的直径,点C在☉O上,AD与过点C的切线互相垂直,垂足为D.连接BC并延长,交AD的延长线于点E.
(1)求证:AE=AB;
(2)若AB=10,BC=6,求CD的长.
图16
参考答案
1.[答案]
B
2.[解析]
D 如图,过点P作PQ⊥y轴于点Q.
∵点P的坐标为(2,3),
∴PQ=2,OQ=3.
∵点P(2,3)绕原点O顺时针旋转90°得到点P',即把△OPQ绕原点O顺时针旋转90°得到△OP'Q',
∴∠P'Q'O=90°,P'Q'=PQ=2,OQ'=OQ=3,
∴点P'的坐标为(3,-2).故选D.
3.[解析]
B ∵=,∴∠BDC=∠ABC=50°,∴∠ADC=180°-∠ABC=130°.故选B.
4.[解析]
C ∵∠ACB=54°,
∴∠AOB=2∠ACB=108°.
∵OB=OA,∴∠ABO=∠BAO=×(180°-∠AOB)=36°.故选C.
5.[解析]
B 如图,作直径BD,连接CD.
由勾股定理,得BD==2.
在Rt△BDC中,cos∠BDC===.
由圆周角定理,得∠BAC=∠BDC,
∴cos∠BAC=cos∠BDC=.故选B.
6.[解析]
A ∵AD为☉O的直径,∴∠ACD=90°.
∵四边形OBCD为平行四边形,
∴CD∥OB,CD=OB,∴CD=OD=AD.
∵OP∥CD,CD⊥AC,
∴OP⊥AC,C选项正确;∴AP=CP.
在Rt△ACD中,sinA==,
∴∠A=30°.
在Rt△AOP中,AP=OP,∴A选项错误;
∵AP=CP,AO=DO,
∴OP为△ACD的中位线,
∴CD=2OP,∴B选项正确;∴OB=2OP,
从而AC平分OB,∴D选项正确.故选A.
7.[解析]
D 如图,作直径CD.
在Rt△OCD中,CD=6,OC=2,
则OD==4,
∴tan∠CDO==.
由圆周角定理,得∠OBC=∠CDO,
则tan∠OBC=.故选D.
8.[解析]
D 如图,过点B作BG⊥AC于点G.
∵BA=BC,BG⊥AC,
∴AG=AC=,∠BAC=∠BCA.
正六边形ABCDEF中,每个内角为(6-2)×180°÷6=120°,
∴∠ABC=120°,∴∠BAC=∠BCA=30°.
在Rt△ABG中,GB=AG·tan∠BAC=×=1,∴AB=2GB=2.即正六边形ABCDEF的边长为2.
故选D.
9.[解析]
C 先利用弧长公式求得圆锥形容器的底面半径,再利用勾股定理求圆锥的高.设圆锥形容器的底面半径为r
m,则有2πr=,解得r=,则圆锥形容器的高为=(m).
10.[解析]
B 如图,连接OE,OF.∵☉O是△ABC的内切圆,E,F是切点,∴OE⊥AB,OF⊥BC,
∴∠OEB=∠OFB=90°.
∵△ABC是等边三角形,∴∠B=60°,
∴∠EOF=120°,∴∠EPF=∠EOF=60°.故选B.
11.[答案]
6
[解析]
如图,连接OB,OC.
∵∠BOC=2∠BAC=60°,又OB=OC,
∴△BOC是等边三角形,∴OB=BC=6.
故答案为6.
12.[答案]
25°
[解析]
∵AC是☉O的切线,
∴OA⊥AC,∴∠OAC=90°,
∴∠AOC=90°-∠C=90°-40°=50°,
∴∠B=∠AOC=25°.
故答案为25°.
13.[答案]
2
[解析]
直角三角形的斜边长==13,
所以它的内切圆半径==2.
故答案为2.
14.[答案]
12
[解析]
设圆锥的母线长为l.
根据题意,得=2π×4,
解得l=12.
故答案为12.
15.[答案]
[解析]
∵M,N分别是AC,BC的中点,
∴MN=AB,
∴当AB取得最大值时,MN就取得最大值,
∴当AB是直径时,MN最大.
如图,连接AO并延长交☉O于点B',连接CB'.
∵AB'是☉O的直径,
∴∠ACB'=90°.
∵∠ABC=45°,
∴∠AB'C=45°,
∴AB'===5,
∴MN最大=.
故答案为.
16.解:如图,连接OA.∵∠ABO=60°,OA=OB,∴△AOB是等边三角形.
∵AB=8,∴☉O的半径为8.
∵AD∥BO,∴∠DAO=∠AOB=60°.
又∵OA=OD,
∴△OAD是等边三角形,∴∠AOD=60°.
∵∠AOB=∠AOD=60°,∴∠DOE=60°.
∵DC⊥BE于点C,
∴CD=OD=4,OC=OD=4,
∴BC=8+4=12,
∴S阴影=S△AOB+S扇形AOD+S扇形DOE-S△BCD=×8×4+2×-×12×4=-8.
17.证明:(1)∵AC=BC,∴∠BAC=∠B.
∵DF∥BC,∴∠ADF=∠B.
又∵∠BAC=∠CFD,∴∠ADF=∠CFD,
∴BD∥CF.
又∵DF∥BC,
∴四边形DBCF是平行四边形.
(2)如图,连接AE.
∵∠ADF=∠B,∠ADF=∠AEF,
∴∠AEF=∠B.
∵四边形AECF是☉O的内接四边形,
∴∠ECF+∠EAF=180°.
∵BD∥CF,∴∠ECF+∠B=180°,
∴∠EAF=∠B,∴∠AEF=∠EAF,
∴AF=EF.
18.解:(1)证明:如图,连接OC.∵CD为切线,∴OC⊥CD.
又∵CD⊥AD,∴OC∥AD,
∴∠OCB=∠E.
∵OB=OC,
∴∠OCB=∠B,
∴∠B=∠E,∴AE=AB.
(2)如图,连接AC.∵AB为直径,∴∠ACB=90°,
∴AC==8.
∵AB=AE=10,AC⊥BE,
∴CE=BC=6.
∵CD·AE=AC·CE,
∴CD==.
