京改版九年级上册21.4圆周角(1)-1教学设计
文档属性
| 名称 | 京改版九年级上册21.4圆周角(1)-1教学设计 |

|
|
| 格式 | zip | ||
| 文件大小 | 228.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-20 00:00:00 | ||
图片预览



文档简介
课程基本信息
课题
圆周角(1)
教科书
书名:《义务教育教科书.数学》
出版社:北京出版社
出版日期:2015年7月
教学目标
教学目标:
1.通过观察、测量、猜想、证明、归纳、探索圆周角定理的过程,理解分类讨论的必要性,渗透由特殊到一般及转化的思想方法.
2.通过对比、分析、归纳圆周角与圆心角的区别与联系,进一步理解圆心角、圆周角、所对弧的度数关系.
3.在定理的探索过程中发展学生的合情推理能力、实践能力及严谨求实的态度.
教学重点:探索圆周角定理
教学难点:圆周角定理的证明.
教学过程
时间
教学环节
主要师生活动
复习
回顾
探索
新知
对比分析
练习巩固
归纳
总结
布置作业
【活动一】
1.在图中任意画一个圆心角,与⊙O交于A、B.
问题:什么是圆心角?如何求出这个圆心角的度数?
预设:顶点在圆心的角是圆心角.转化为圆心角所对弧的度数.
问题:劣弧所对圆心角有几个?(只有一个)
【活动二】
问题:如果只改变顶点的位置,除了圆心外还可以在哪里?
预设:顶点C在圆外,在圆上,在圆内(不含圆心).
顶点C在圆上;顶点C在圆内(不含圆心);
顶点C在圆外.
师:本节课我们一起研究顶点在圆上的角.
问题:图中的有什么特征?
预设:角的顶点C在圆上,角的两条边CA、CB与圆相交.我们把符合这些特点的角叫做圆周角.
问题:什么是圆周角?
预设:圆周角是顶点在圆上,两边都与圆相交的角.
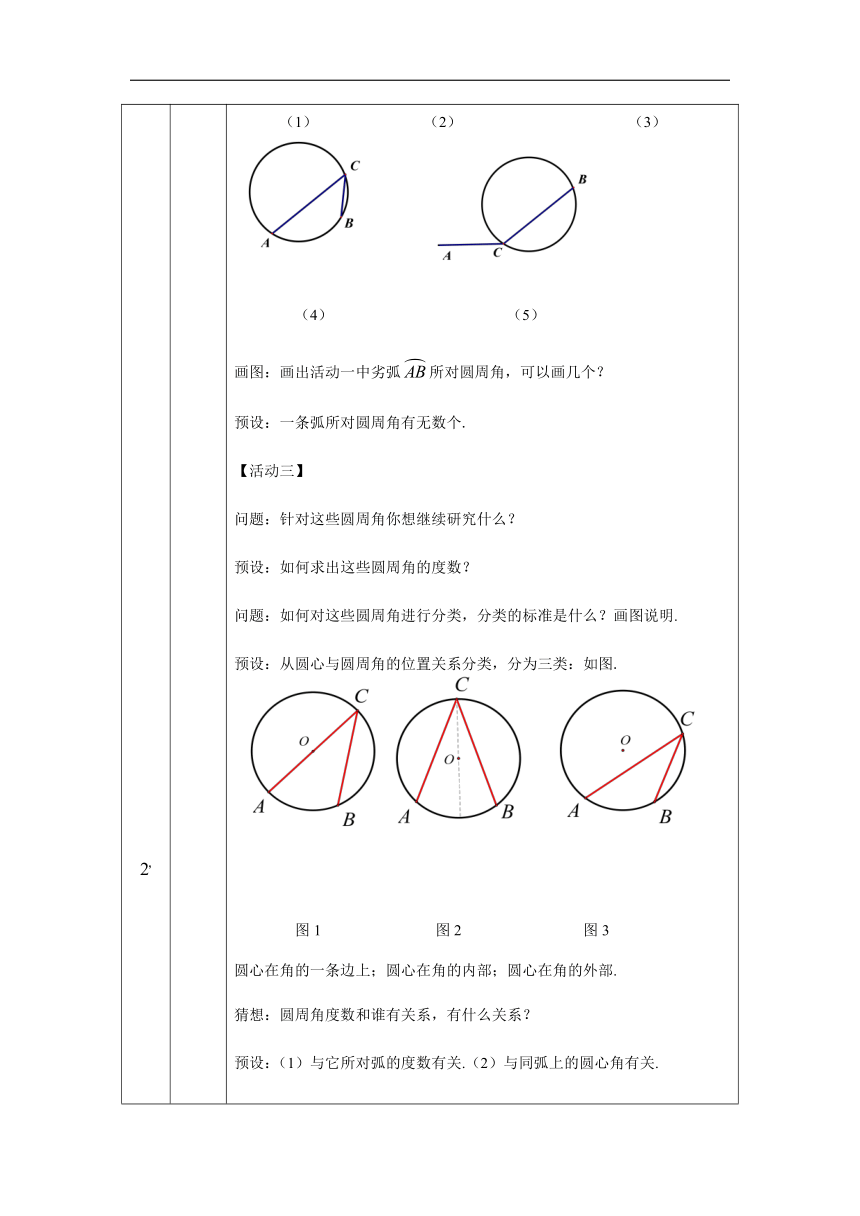
判断:下列各图中的角是不是圆周角,并说理.
(1)
(2)
(3)
(4)
(5)
画图:画出活动一中劣弧所对圆周角,可以画几个?
预设:一条弧所对圆周角有无数个.
【活动三】
问题:针对这些圆周角你想继续研究什么?
预设:如何求出这些圆周角的度数?
问题:如何对这些圆周角进行分类,分类的标准是什么?画图说明.
预设:从圆心与圆周角的位置关系分类,分为三类:如图.
图1
图2
图3
圆心在角的一条边上;圆心在角的内部;圆心在角的外部.
猜想:圆周角度数和谁有关系,有什么关系?
预设:(1)与它所对弧的度数有关.(2)与同弧上的圆心角有关.
【活动四】
1.动手实验,发现猜想
分别测量所画的三种情况圆周角、圆心角的度数,猜想它们的关系.(结果保留整数)
分类圆周角圆心角弧度三者的关系圆心在角的一条边上圆心在角的内部圆心在角的外部
预设:(1)圆周角度数等于所对弧的度数的一半.
(2)圆周角度数等于同弧上圆心角度数的一半.
猜想:一条弧所对的圆周角等于它所对的圆心角的一半.
2.说理论证,证明猜想
问题:如何证明猜想?已知、求证分别是什么?
已知:在⊙O中,所对的圆周角是∠ACB,圆心角是∠AOB.
求证:∠ACB=∠AOB.
问题:是否上述三种情况都需要证明?如果都要证明,先证哪一种情况,为什么?
预设:第一类情况最特殊容易验证,第二、第三类情况教师引导学生由圆的轴对称性联想到作辅助线“直径”,可以把第二、第三类情况转化为第一类来验证.
第一类:圆心在圆周角的边上
∠C=∠AOB∠B=∠COB=OC
第二类:圆心在圆周角内部
∠C=∠AOB∠ACD+∠BCD=(∠AOD+∠BOD
)∠ACD=
∠AOD、∠BCD=∠BOD
第三类:圆心在圆周角外部
∠C=∠AOB∠BCD─∠ACD
=(∠BOD─∠AOD)∠ACD=
∠AOD、∠BCD=∠BOD
3.语言表述,归纳定理
圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半.
∵所对的圆周角是∠ACB,圆心角是∠AOB,
∴∠C=∠AOB.
【活动五】填表,对比圆心角与圆周角.
角定义图形定理三者的关系圆心角圆周角
【活动六】练习
1.如图1,A、B、C、D四点都在⊙O上,∠BOC=100o,你还可以求哪些角或弧的度数?
图1
2.
如图2,在⊙O中,AB是⊙O的直径,为108°,求∠AOC的度数.
图2
变式1:如图2,在⊙O中,AB是⊙O的直径,∠BOC=72°,求∠AOC的度数.
变式2:如图2,在⊙O中,AB是⊙O的直径,为72°,求∠AOC的度数.
变式3:如图2,在⊙O中,AB是⊙O的直径,∠D=36°,求∠AOC的度数.
【活动七】小结
本节课我们都学习了哪些知识,我们是如何研究的?
【活动八】作业
1.如图1,半径为2,∠BDA=45°,则AB=
.
图1
2.如图2,∠A是⊙O的圆周角,∠A=40°,则∠OBC
=
°.
图2
3.在⊙O中,BC是弦,∠BOC=100o,则BC所对的圆周角是
°.
4.如图3,AD是⊙O直径,,∠A=30°,则∠B=
°.
图3
5.如图4,求∠A+∠B+∠C+∠D+∠E=
°.
图4
课题
圆周角(1)
教科书
书名:《义务教育教科书.数学》
出版社:北京出版社
出版日期:2015年7月
教学目标
教学目标:
1.通过观察、测量、猜想、证明、归纳、探索圆周角定理的过程,理解分类讨论的必要性,渗透由特殊到一般及转化的思想方法.
2.通过对比、分析、归纳圆周角与圆心角的区别与联系,进一步理解圆心角、圆周角、所对弧的度数关系.
3.在定理的探索过程中发展学生的合情推理能力、实践能力及严谨求实的态度.
教学重点:探索圆周角定理
教学难点:圆周角定理的证明.
教学过程
时间
教学环节
主要师生活动
复习
回顾
探索
新知
对比分析
练习巩固
归纳
总结
布置作业
【活动一】
1.在图中任意画一个圆心角,与⊙O交于A、B.
问题:什么是圆心角?如何求出这个圆心角的度数?
预设:顶点在圆心的角是圆心角.转化为圆心角所对弧的度数.
问题:劣弧所对圆心角有几个?(只有一个)
【活动二】
问题:如果只改变顶点的位置,除了圆心外还可以在哪里?
预设:顶点C在圆外,在圆上,在圆内(不含圆心).
顶点C在圆上;顶点C在圆内(不含圆心);
顶点C在圆外.
师:本节课我们一起研究顶点在圆上的角.
问题:图中的有什么特征?
预设:角的顶点C在圆上,角的两条边CA、CB与圆相交.我们把符合这些特点的角叫做圆周角.
问题:什么是圆周角?
预设:圆周角是顶点在圆上,两边都与圆相交的角.
判断:下列各图中的角是不是圆周角,并说理.
(1)
(2)
(3)
(4)
(5)
画图:画出活动一中劣弧所对圆周角,可以画几个?
预设:一条弧所对圆周角有无数个.
【活动三】
问题:针对这些圆周角你想继续研究什么?
预设:如何求出这些圆周角的度数?
问题:如何对这些圆周角进行分类,分类的标准是什么?画图说明.
预设:从圆心与圆周角的位置关系分类,分为三类:如图.
图1
图2
图3
圆心在角的一条边上;圆心在角的内部;圆心在角的外部.
猜想:圆周角度数和谁有关系,有什么关系?
预设:(1)与它所对弧的度数有关.(2)与同弧上的圆心角有关.
【活动四】
1.动手实验,发现猜想
分别测量所画的三种情况圆周角、圆心角的度数,猜想它们的关系.(结果保留整数)
分类圆周角圆心角弧度三者的关系圆心在角的一条边上圆心在角的内部圆心在角的外部
预设:(1)圆周角度数等于所对弧的度数的一半.
(2)圆周角度数等于同弧上圆心角度数的一半.
猜想:一条弧所对的圆周角等于它所对的圆心角的一半.
2.说理论证,证明猜想
问题:如何证明猜想?已知、求证分别是什么?
已知:在⊙O中,所对的圆周角是∠ACB,圆心角是∠AOB.
求证:∠ACB=∠AOB.
问题:是否上述三种情况都需要证明?如果都要证明,先证哪一种情况,为什么?
预设:第一类情况最特殊容易验证,第二、第三类情况教师引导学生由圆的轴对称性联想到作辅助线“直径”,可以把第二、第三类情况转化为第一类来验证.
第一类:圆心在圆周角的边上
∠C=∠AOB∠B=∠COB=OC
第二类:圆心在圆周角内部
∠C=∠AOB∠ACD+∠BCD=(∠AOD+∠BOD
)∠ACD=
∠AOD、∠BCD=∠BOD
第三类:圆心在圆周角外部
∠C=∠AOB∠BCD─∠ACD
=(∠BOD─∠AOD)∠ACD=
∠AOD、∠BCD=∠BOD
3.语言表述,归纳定理
圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半.
∵所对的圆周角是∠ACB,圆心角是∠AOB,
∴∠C=∠AOB.
【活动五】填表,对比圆心角与圆周角.
角定义图形定理三者的关系圆心角圆周角
【活动六】练习
1.如图1,A、B、C、D四点都在⊙O上,∠BOC=100o,你还可以求哪些角或弧的度数?
图1
2.
如图2,在⊙O中,AB是⊙O的直径,为108°,求∠AOC的度数.
图2
变式1:如图2,在⊙O中,AB是⊙O的直径,∠BOC=72°,求∠AOC的度数.
变式2:如图2,在⊙O中,AB是⊙O的直径,为72°,求∠AOC的度数.
变式3:如图2,在⊙O中,AB是⊙O的直径,∠D=36°,求∠AOC的度数.
【活动七】小结
本节课我们都学习了哪些知识,我们是如何研究的?
【活动八】作业
1.如图1,半径为2,∠BDA=45°,则AB=
.
图1
2.如图2,∠A是⊙O的圆周角,∠A=40°,则∠OBC
=
°.
图2
3.在⊙O中,BC是弦,∠BOC=100o,则BC所对的圆周角是
°.
4.如图3,AD是⊙O直径,,∠A=30°,则∠B=
°.
图3
5.如图4,求∠A+∠B+∠C+∠D+∠E=
°.
图4
同课章节目录
- 第十八章 相似形
- 18.1 比例线段
- 18.2 黄金分割
- 18.3 平行线分三角形两边成比例
- 18.4 相似多边形
- 18.5 相似三角形的判定
- 18.6 相似三角形的性质
- 18.7 应用举例
- 第十九章 二次函数和反比例函数
- 19.1 二次函数
- 19.2 二次函数 y=ax2+bx+c(a≠0) 的图象
- 19.3 二次函数的性质
- 19.4 二次函数的应用
- 19.5 反比例函数
- 19.6 反比例函数的图象、性质和应用
- 第二十章 解直角三角形
- 20.1 锐角三角函数
- 20.2 30°、45°、60° 角的三角函数值
- 20.3 用科学计算器求锐角三角函数值
- 20.4 解直角三角形
- 20.5 测量与计算
- 第二十一章 圆(上)
- 21.1 圆的有关概念
- 21.2 过三点的圆
- 21.3 圆的对称性
- 21.4 圆周角
- 第二十二章 圆(下)
- 22.1 直线和圆的位置关系
- 22.2 圆的切线
- 22.3 正多边形的有关计算
