人教版九年级数学下册 第二十七章 相似 综合训练题(word版含答案)
文档属性
| 名称 | 人教版九年级数学下册 第二十七章 相似 综合训练题(word版含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-20 00:00:00 | ||
图片预览


文档简介
人教版九年级数学下册
第二十七章
相似
综合训练题
一、选择题
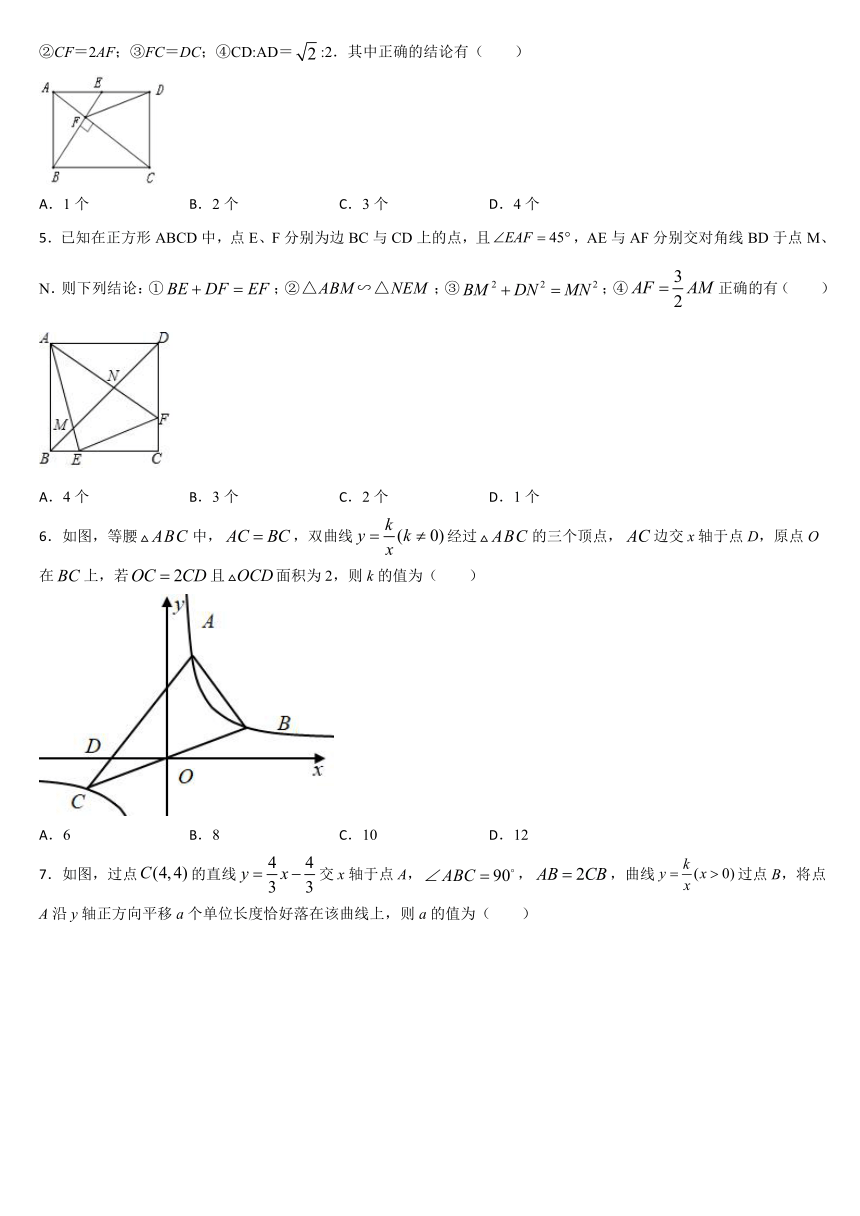
1.如图,在矩形中,,分别为边,的中点,线段,与对角线分别交于点,.设矩形的面积为,则以下4个结论中:①;②;③;④.正确的结论有(
)
A.1个
B.2个
C.3个
D.4个
2.如图,在△ABC中,过点A作AE⊥BC于点E,过点C作CD⊥AB于点D,AE,CD交于点F,连接BF.将△ABF沿BF翻折得到△A′BF,点A′恰好落在线段AC上且BA′交CD于点G,若AE=EC,AC=3,BE=1,则BG=( )
A.5
B.
C.
D.3
3.如图,点M是正方形内一点,是等边三角形,连接、.对角线交于点N,现有以下结论:①;②;③;④,其中正确的结论有( )
A.①②③④
B.②③
C.①②④
D.①③④
4.如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③FC=DC;④CD:AD=:2.其中正确的结论有(
)
A.1个
B.2个
C.3个
D.4个
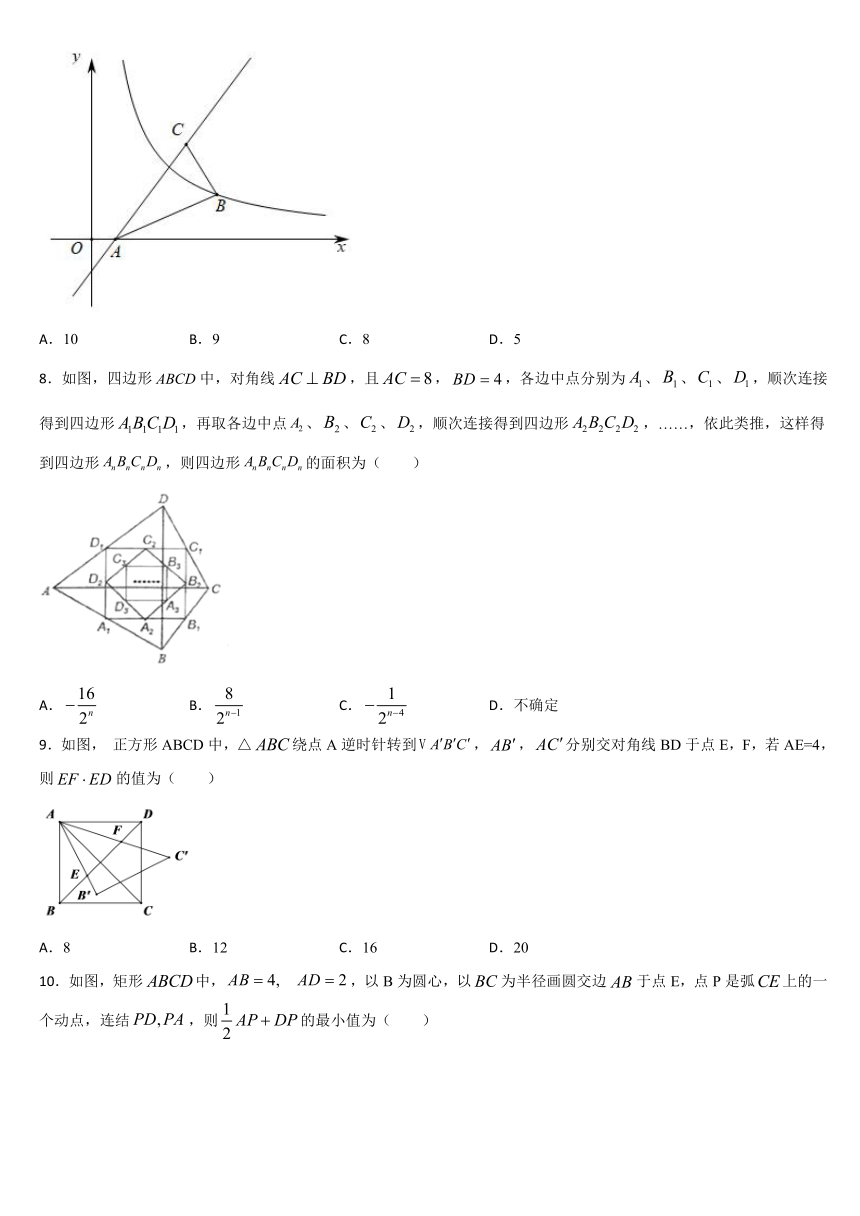
5.已知在正方形ABCD中,点E、F分别为边BC与CD上的点,且,AE与AF分别交对角线BD于点M、N.则下列结论:①;②;③;④正确的有(
)
A.4个
B.3个
C.2个
D.1个
6.如图,等腰中,,双曲线经过的三个顶点,边交x轴于点D,原点O在上,若且面积为2,则k的值为(
)
A.6
B.8
C.10
D.12
7.如图,过点的直线交x轴于点A,,,曲线过点B,将点A沿y轴正方向平移a个单位长度恰好落在该曲线上,则a的值为(
)
A.10
B.9
C.8
D.5
8.如图,四边形ABCD中,对角线,且,,各边中点分别为、、、,顺次连接得到四边形,再取各边中点、、、,顺次连接得到四边形,……,依此类推,这样得到四边形,则四边形的面积为(
)
A.
B.
C.
D.不确定
9.如图,
正方形ABCD中,△绕点A逆时针转到,,分别交对角线BD于点E,F,若AE=4,则的值为(
)
A.8
B.12
C.16
D.20
10.如图,矩形中,,以B为圆心,以为半径画圆交边于点E,点P是弧上的一个动点,连结,则的最小值为(
)
A.
B.
C.
D.
第II卷(非选择题)
请点击修改第II卷的文字说明
二、填空题
11.如图,,∠ABO=30°,M为的中点,,将绕点O旋转一周,直线交于点P,连接,则的最小值是__________.
12.如图,是边长为等边三角形,动点P、Q同时从A、B出发,分别沿、方向匀速运动,其中点P运动的速度是,点Q运动的速度是,当点Q到达点C时,P、Q两点停止运动,在运动过程中作交于点R,连接,设运动的时间为,当t=__________s时.
13.如图,正方形中,,点是对角线上的一点,连接.过点作,交于点,以、为邻边作矩形,连接.①矩形是正方形;②;③;④若为中点,连接交于点,则,正确的有________.(填序号).
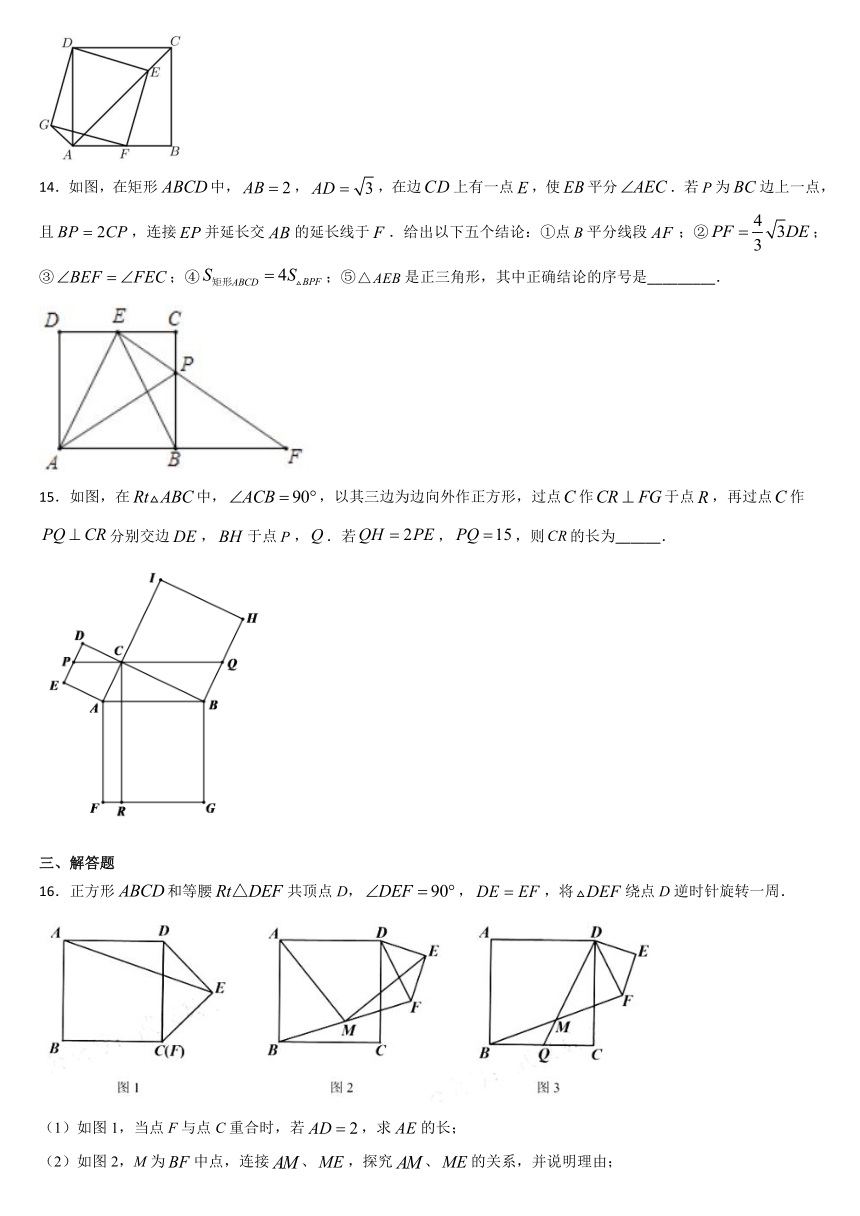
14.如图,在矩形中,,,在边上有一点,使平分.若为边上一点,且,连接并延长交的延长线于.给出以下五个结论:①点平分线段;②;③;④;⑤是正三角形,其中正确结论的序号是_________.
15.如图,在中,,以其三边为边向外作正方形,过点作于点,再过点作分别交边,于点,.若,,则的长为______.
三、解答题
16.正方形和等腰共顶点D,,,将绕点D逆时针旋转一周.
(1)如图1,当点F与点C重合时,若,求的长;
(2)如图2,M为中点,连接、,探究、的关系,并说明理由;
(3)如图3,在(2)条件下,连接并延长交于点Q,若,在旋转过程中,的最小值为_________.
17.如图1
,已知中,,点在、上,且.
(1)求证:.
(2)如图,过点作交于点,作交于点,求证:.
(3)在图
2中,
与交于点,若,求的值.
18.如图,在矩形中,点C在x轴上,点B的坐标是.矩形沿直线折叠,使得点A落在对角线上的点E处,且直线与、x轴分别交于点D、F.
(1)求线段的长;
(2)求直线的解析式;
(3)若点P是平面内任意一点,点M是直线上的一个动点,过点M作轴,垂足为点N.在点M的运动过程中是否存在以P、N、E、O为顶点的四边形是菱形,且该菱形的一边为.若存在,直接写出点M的坐标;若不存在,请说明理由.
19.如图1,在中,是边上一点,E是在边上的一个动点(与点不重合),与射线相交于点F.
(1)如图2,如果点D是边的中点,求证:;
(2)如果,求的值;
(3)如果,设,求y关于x的函数关系式,并写出定义域;
20.如图,在中,,,.点从点开始沿边向点以每秒的速度移动,点从点开始沿边向点以每秒的速度移动,点,分别从点,同时出发,且当一点到达终点时,另一点也停止运动.
(1)经过多少秒,可使的面积等于?
(2)经过多少秒,与相似?
(3)线段能否将分成面积相等的两部分?若能,求出运动时间;若不能,请说明理由.
21.如图,中,,是斜边上一个动点,以为直径作交于点,与的另一个交点,连接.
(1)当时,
①若,求的度数;
②求证;
(2)当,时,是否存在点,使得是等腰三角形,若存在,求出所有符合条件的的长.
22.如图,是的中位线,是的中点,的延长线交于点,若的面积为4,求四边形的面积.
23.如图1,在矩形中,,,为中点,是线段上一动点,以为圆心,为半径作⊙分别交及延长线于点,,延长交于点.
(1)当时,求的长.
(2)如图2,当交⊙于另一点时,连接,,作于点,求证:.
(3)连结,当是直角三角形时,求的长.
【参考答案】
1.C
2.C
3.A
4.C
5.B
6.A
7.A
8.B
9.C
10.C
11.6-.
12.
13.①③④
14.①②③⑤
15.14
16.解:(1)过点作交延长线于点,如图:
∵四边形为正方形
∴,
∵,
∴,
∴
∴
∴.
(2)结论:,
理由:延长至,使,连接、,延长、交于点,如图:
∵,
∴
∴,
∴
∴
∴
∴
∴
∴,
∴,.
(3)根据已知条件可知若越小,则即越靠近点,而点是的中点,点位置不变,而点的位置改变,由于绕点D逆时针旋转一周且可知点的运动轨迹为:以点为圆心以为半径的圆,不难看出当点、、共线即旋转到时,最小,过点作、,过点作交的延长线于点,如图:
∴,点是的中点
∴,且相似比为;,
即
∴,;
∴
∵,点是的中点
∴,且相似比为
∴
∴的最小值为.
17.(1)在与中,
,
∴,
∴,
∵,
∴,
∴,
即;
(2)如图,过点作交的延长线于,
∵,
∴,
又∵,
∴,
在与中
,
∴,
∴,
∵,
∴,
∴,
∴,
又∵,
∴,
∵,,
∴,
∴,
∴,
∴,
∴;
(3)由(2)得,
又,
∴,
∴,
∵,
∴设,
已证:,,
∴,
∴,
∴,
代入得,
∴,
由,得,
∴,
∴,
作的高,
则,
∴
.
18.解:(1)由B(-6,8)可得OC=6,BC=8.
∵四边形ABCO是矩形,
∴∠BCO=90°,
由勾股定理可得:BO=
,
由折叠可知BE=BA=6,
∴EO=OB-BE=10-6=4.
(2)设D(0,b),则由题意可得:∠DEO=90°,DE=DA=8-b,
在直角三角形DEO中由勾股定理可列:OE2+DE2=DO2,
即42+(8-b)2=b2,
解得b=5,
所以D(0,5)
∴设直线BD的解析式为y=kx+5,
把B(-6,8)代入得8=-6k+5,,
∴,
所以直线BD的解析式为:;
(3)当ON是菱形的一边时,即ON=OE=4,
所以N?(4,0)或N?(-4,0),
此时分别将4和-4代入,
得点M的坐标为(4,3)或(-4,7).
当ON是菱形的对角线时,即NE=OE时,作NH⊥OC于H,如图,
可知,
∴,
∴,
∴,
∴,
把代入得点M的坐标为,
综上所述:在点M的运动过程中存在以P、N、E、O为顶点的四边形是菱形.点M的坐标为:(4,3)或(-4,7)或.
19.(1)证明:如图2,连接DC.
∵∠ACB=90°,AC=BC,
∴∠A=∠B=45°,
∵点D是AB中点,
∴∠BCD=∠ACD=45°,CD=BD,
∴∠ACD=∠B=45°.
∵ED⊥DF,CD⊥AB,
∴∠EDC+∠CDF=90°,∠CDF+∠FDB=90°,
∴∠EDC=∠FDB,
∴△CED≌△BFD(ASA),
∴DE=DF;
(2)解:如图1,作DP⊥AC,DQ⊥BC,垂足分别为点Q,P.
∵∠B=∠A,∠APD=∠BQD=90°,
∴△ADP∽△BDQ,
∴DP:DQ=AD:DB=k.
∵∠CPD=∠CQD=90°,∠C=90°,
∴∠QDP=90°,
∵DF⊥DE,∴∠EDF=90°,
∴∠QDF=∠PDE,
∵∠DQF=∠DPE=90°,
∴△DQF∽△DPE,
∴DE:DF=DP:DQ,
∴DE:DF=DP:DQ=AD:DB=k;
(3)解:如备用图1,作EG⊥AB,FH⊥AB,垂足分别为点G、H.
在Rt△ABC中,∠C=90°,AC=BC=6,
∴AB=
∵AD:DB=1:2,
∴AD=2,DB=4.
由∠AGE=∠BHF=90°,∠A=∠B=45°,
可得AG=EG=x,BH=FH=y,
GD=2-x,HD=4-y,
∵DF⊥DE
∴∠EDF=90°,
∴∠GED=∠HDF,∠EDG=∠DFH
∴△DGE∽△FHD,
∴y=8-2x,
定义域是0<x≤4.
20.(1)设经过秒,可使的面积等于.
由题意列方程,得
整理,得,
解得,,
即经过2秒或4秒,可使的面积等于.
(2)设经过秒,与相似.
情况1:若,
则,即,
解得;
情况2:若,
则,即,
解得.
综上,经过2.4秒或秒时,与相似.
(3)线段不能将分成面积相等的两部分.
理由:假设经过秒线段能将分成面积相等的两部分,
则,
整理得,,,
∴此方程无实根,即假设不成立,
∴线段不能将分成面积相等的两部分.
21.(1)①解:连接,如图1所示:
是直径,
,
,
,
,
,
,
;
②证明:,
,
,,
,,,
,
;
(2)解:由,,
由勾股定理得:,
,
即
,
连接,如图所示:
是直径,
,
,
,
,
,
,
是等腰三角形,分三种情况:
当时,,
,
;
当时,可知点是斜边的中线,
,
;
当时,作,则是中点,,如图所示:
,
,,
,
,
即,
解得:,
,
,
;
综上所述,是等腰三角形,符合条件的的长为10或或7.
22.解:作于交于,
是的中位线,
,,
是的中点,
,
,
,
,
,,
∴
∵,
∴,
即有:,
∴
即,
∴
∵,
∴
即,
∴.
23.解:(1)如图1中,
∵四边形ABCD是矩形,
∴∠BAD=90°,AD∥BC,
∵AB=3,AO=OD=4,
∴OB==5,
∵OP=OE=2,
∴BE=3,
∵BH∥OA,
∴=,
∴=,
∴BH=6.
(2)如图2中,
∵EF是直径,
∴∠EGF=90°,
∵OA=OD,∠AOE=∠DOF,OE=OF,
∴AOE≌DOF(SAS),
∴∠EAO=∠ODF,
∴AH∥DF,
∴∠DFG=∠EGF=90°,
∵DM⊥BF,
∴∠DMF=∠EGF=90°,
∵∠GFE+∠DFM=90°,∠DFM+∠FDM=90°,
∴∠EFG=∠FDM,
∴EFG∽FDM.
(3)如图3﹣1中,当∠HEO=90°时,
∵?AB?AO=?OB?AE,
∴AE=,
∴OE==,
∴OP=OE=.
如图3﹣2中,当∠EOH=90°时,
∵BC∥AD,
∴∠BOA=∠OBH,
∵∠BAO=∠BOH=90°,
∴ABO∽OHB,
∴=,
∴=,
∴BH=,
∵OA∥BH,
∴===,
∴OE=?OB=,
∴OP=OE=,
综上所述,OP的值为或.
第二十七章
相似
综合训练题
一、选择题
1.如图,在矩形中,,分别为边,的中点,线段,与对角线分别交于点,.设矩形的面积为,则以下4个结论中:①;②;③;④.正确的结论有(
)
A.1个
B.2个
C.3个
D.4个
2.如图,在△ABC中,过点A作AE⊥BC于点E,过点C作CD⊥AB于点D,AE,CD交于点F,连接BF.将△ABF沿BF翻折得到△A′BF,点A′恰好落在线段AC上且BA′交CD于点G,若AE=EC,AC=3,BE=1,则BG=( )
A.5
B.
C.
D.3
3.如图,点M是正方形内一点,是等边三角形,连接、.对角线交于点N,现有以下结论:①;②;③;④,其中正确的结论有( )
A.①②③④
B.②③
C.①②④
D.①③④
4.如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③FC=DC;④CD:AD=:2.其中正确的结论有(
)
A.1个
B.2个
C.3个
D.4个
5.已知在正方形ABCD中,点E、F分别为边BC与CD上的点,且,AE与AF分别交对角线BD于点M、N.则下列结论:①;②;③;④正确的有(
)
A.4个
B.3个
C.2个
D.1个
6.如图,等腰中,,双曲线经过的三个顶点,边交x轴于点D,原点O在上,若且面积为2,则k的值为(
)
A.6
B.8
C.10
D.12
7.如图,过点的直线交x轴于点A,,,曲线过点B,将点A沿y轴正方向平移a个单位长度恰好落在该曲线上,则a的值为(
)
A.10
B.9
C.8
D.5
8.如图,四边形ABCD中,对角线,且,,各边中点分别为、、、,顺次连接得到四边形,再取各边中点、、、,顺次连接得到四边形,……,依此类推,这样得到四边形,则四边形的面积为(
)
A.
B.
C.
D.不确定
9.如图,
正方形ABCD中,△绕点A逆时针转到,,分别交对角线BD于点E,F,若AE=4,则的值为(
)
A.8
B.12
C.16
D.20
10.如图,矩形中,,以B为圆心,以为半径画圆交边于点E,点P是弧上的一个动点,连结,则的最小值为(
)
A.
B.
C.
D.
第II卷(非选择题)
请点击修改第II卷的文字说明
二、填空题
11.如图,,∠ABO=30°,M为的中点,,将绕点O旋转一周,直线交于点P,连接,则的最小值是__________.
12.如图,是边长为等边三角形,动点P、Q同时从A、B出发,分别沿、方向匀速运动,其中点P运动的速度是,点Q运动的速度是,当点Q到达点C时,P、Q两点停止运动,在运动过程中作交于点R,连接,设运动的时间为,当t=__________s时.
13.如图,正方形中,,点是对角线上的一点,连接.过点作,交于点,以、为邻边作矩形,连接.①矩形是正方形;②;③;④若为中点,连接交于点,则,正确的有________.(填序号).
14.如图,在矩形中,,,在边上有一点,使平分.若为边上一点,且,连接并延长交的延长线于.给出以下五个结论:①点平分线段;②;③;④;⑤是正三角形,其中正确结论的序号是_________.
15.如图,在中,,以其三边为边向外作正方形,过点作于点,再过点作分别交边,于点,.若,,则的长为______.
三、解答题
16.正方形和等腰共顶点D,,,将绕点D逆时针旋转一周.
(1)如图1,当点F与点C重合时,若,求的长;
(2)如图2,M为中点,连接、,探究、的关系,并说明理由;
(3)如图3,在(2)条件下,连接并延长交于点Q,若,在旋转过程中,的最小值为_________.
17.如图1
,已知中,,点在、上,且.
(1)求证:.
(2)如图,过点作交于点,作交于点,求证:.
(3)在图
2中,
与交于点,若,求的值.
18.如图,在矩形中,点C在x轴上,点B的坐标是.矩形沿直线折叠,使得点A落在对角线上的点E处,且直线与、x轴分别交于点D、F.
(1)求线段的长;
(2)求直线的解析式;
(3)若点P是平面内任意一点,点M是直线上的一个动点,过点M作轴,垂足为点N.在点M的运动过程中是否存在以P、N、E、O为顶点的四边形是菱形,且该菱形的一边为.若存在,直接写出点M的坐标;若不存在,请说明理由.
19.如图1,在中,是边上一点,E是在边上的一个动点(与点不重合),与射线相交于点F.
(1)如图2,如果点D是边的中点,求证:;
(2)如果,求的值;
(3)如果,设,求y关于x的函数关系式,并写出定义域;
20.如图,在中,,,.点从点开始沿边向点以每秒的速度移动,点从点开始沿边向点以每秒的速度移动,点,分别从点,同时出发,且当一点到达终点时,另一点也停止运动.
(1)经过多少秒,可使的面积等于?
(2)经过多少秒,与相似?
(3)线段能否将分成面积相等的两部分?若能,求出运动时间;若不能,请说明理由.
21.如图,中,,是斜边上一个动点,以为直径作交于点,与的另一个交点,连接.
(1)当时,
①若,求的度数;
②求证;
(2)当,时,是否存在点,使得是等腰三角形,若存在,求出所有符合条件的的长.
22.如图,是的中位线,是的中点,的延长线交于点,若的面积为4,求四边形的面积.
23.如图1,在矩形中,,,为中点,是线段上一动点,以为圆心,为半径作⊙分别交及延长线于点,,延长交于点.
(1)当时,求的长.
(2)如图2,当交⊙于另一点时,连接,,作于点,求证:.
(3)连结,当是直角三角形时,求的长.
【参考答案】
1.C
2.C
3.A
4.C
5.B
6.A
7.A
8.B
9.C
10.C
11.6-.
12.
13.①③④
14.①②③⑤
15.14
16.解:(1)过点作交延长线于点,如图:
∵四边形为正方形
∴,
∵,
∴,
∴
∴
∴.
(2)结论:,
理由:延长至,使,连接、,延长、交于点,如图:
∵,
∴
∴,
∴
∴
∴
∴
∴
∴,
∴,.
(3)根据已知条件可知若越小,则即越靠近点,而点是的中点,点位置不变,而点的位置改变,由于绕点D逆时针旋转一周且可知点的运动轨迹为:以点为圆心以为半径的圆,不难看出当点、、共线即旋转到时,最小,过点作、,过点作交的延长线于点,如图:
∴,点是的中点
∴,且相似比为;,
即
∴,;
∴
∵,点是的中点
∴,且相似比为
∴
∴的最小值为.
17.(1)在与中,
,
∴,
∴,
∵,
∴,
∴,
即;
(2)如图,过点作交的延长线于,
∵,
∴,
又∵,
∴,
在与中
,
∴,
∴,
∵,
∴,
∴,
∴,
又∵,
∴,
∵,,
∴,
∴,
∴,
∴,
∴;
(3)由(2)得,
又,
∴,
∴,
∵,
∴设,
已证:,,
∴,
∴,
∴,
代入得,
∴,
由,得,
∴,
∴,
作的高,
则,
∴
.
18.解:(1)由B(-6,8)可得OC=6,BC=8.
∵四边形ABCO是矩形,
∴∠BCO=90°,
由勾股定理可得:BO=
,
由折叠可知BE=BA=6,
∴EO=OB-BE=10-6=4.
(2)设D(0,b),则由题意可得:∠DEO=90°,DE=DA=8-b,
在直角三角形DEO中由勾股定理可列:OE2+DE2=DO2,
即42+(8-b)2=b2,
解得b=5,
所以D(0,5)
∴设直线BD的解析式为y=kx+5,
把B(-6,8)代入得8=-6k+5,,
∴,
所以直线BD的解析式为:;
(3)当ON是菱形的一边时,即ON=OE=4,
所以N?(4,0)或N?(-4,0),
此时分别将4和-4代入,
得点M的坐标为(4,3)或(-4,7).
当ON是菱形的对角线时,即NE=OE时,作NH⊥OC于H,如图,
可知,
∴,
∴,
∴,
∴,
把代入得点M的坐标为,
综上所述:在点M的运动过程中存在以P、N、E、O为顶点的四边形是菱形.点M的坐标为:(4,3)或(-4,7)或.
19.(1)证明:如图2,连接DC.
∵∠ACB=90°,AC=BC,
∴∠A=∠B=45°,
∵点D是AB中点,
∴∠BCD=∠ACD=45°,CD=BD,
∴∠ACD=∠B=45°.
∵ED⊥DF,CD⊥AB,
∴∠EDC+∠CDF=90°,∠CDF+∠FDB=90°,
∴∠EDC=∠FDB,
∴△CED≌△BFD(ASA),
∴DE=DF;
(2)解:如图1,作DP⊥AC,DQ⊥BC,垂足分别为点Q,P.
∵∠B=∠A,∠APD=∠BQD=90°,
∴△ADP∽△BDQ,
∴DP:DQ=AD:DB=k.
∵∠CPD=∠CQD=90°,∠C=90°,
∴∠QDP=90°,
∵DF⊥DE,∴∠EDF=90°,
∴∠QDF=∠PDE,
∵∠DQF=∠DPE=90°,
∴△DQF∽△DPE,
∴DE:DF=DP:DQ,
∴DE:DF=DP:DQ=AD:DB=k;
(3)解:如备用图1,作EG⊥AB,FH⊥AB,垂足分别为点G、H.
在Rt△ABC中,∠C=90°,AC=BC=6,
∴AB=
∵AD:DB=1:2,
∴AD=2,DB=4.
由∠AGE=∠BHF=90°,∠A=∠B=45°,
可得AG=EG=x,BH=FH=y,
GD=2-x,HD=4-y,
∵DF⊥DE
∴∠EDF=90°,
∴∠GED=∠HDF,∠EDG=∠DFH
∴△DGE∽△FHD,
∴y=8-2x,
定义域是0<x≤4.
20.(1)设经过秒,可使的面积等于.
由题意列方程,得
整理,得,
解得,,
即经过2秒或4秒,可使的面积等于.
(2)设经过秒,与相似.
情况1:若,
则,即,
解得;
情况2:若,
则,即,
解得.
综上,经过2.4秒或秒时,与相似.
(3)线段不能将分成面积相等的两部分.
理由:假设经过秒线段能将分成面积相等的两部分,
则,
整理得,,,
∴此方程无实根,即假设不成立,
∴线段不能将分成面积相等的两部分.
21.(1)①解:连接,如图1所示:
是直径,
,
,
,
,
,
,
;
②证明:,
,
,,
,,,
,
;
(2)解:由,,
由勾股定理得:,
,
即
,
连接,如图所示:
是直径,
,
,
,
,
,
,
是等腰三角形,分三种情况:
当时,,
,
;
当时,可知点是斜边的中线,
,
;
当时,作,则是中点,,如图所示:
,
,,
,
,
即,
解得:,
,
,
;
综上所述,是等腰三角形,符合条件的的长为10或或7.
22.解:作于交于,
是的中位线,
,,
是的中点,
,
,
,
,
,,
∴
∵,
∴,
即有:,
∴
即,
∴
∵,
∴
即,
∴.
23.解:(1)如图1中,
∵四边形ABCD是矩形,
∴∠BAD=90°,AD∥BC,
∵AB=3,AO=OD=4,
∴OB==5,
∵OP=OE=2,
∴BE=3,
∵BH∥OA,
∴=,
∴=,
∴BH=6.
(2)如图2中,
∵EF是直径,
∴∠EGF=90°,
∵OA=OD,∠AOE=∠DOF,OE=OF,
∴AOE≌DOF(SAS),
∴∠EAO=∠ODF,
∴AH∥DF,
∴∠DFG=∠EGF=90°,
∵DM⊥BF,
∴∠DMF=∠EGF=90°,
∵∠GFE+∠DFM=90°,∠DFM+∠FDM=90°,
∴∠EFG=∠FDM,
∴EFG∽FDM.
(3)如图3﹣1中,当∠HEO=90°时,
∵?AB?AO=?OB?AE,
∴AE=,
∴OE==,
∴OP=OE=.
如图3﹣2中,当∠EOH=90°时,
∵BC∥AD,
∴∠BOA=∠OBH,
∵∠BAO=∠BOH=90°,
∴ABO∽OHB,
∴=,
∴=,
∴BH=,
∵OA∥BH,
∴===,
∴OE=?OB=,
∴OP=OE=,
综上所述,OP的值为或.
