北师大版数学七年级下册4.1.4三角形的高线 课件(15张PPT)
文档属性
| 名称 | 北师大版数学七年级下册4.1.4三角形的高线 课件(15张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 361.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-24 10:19:43 | ||
图片预览



文档简介
第四章 三角形
1 认识三角形
课时4 三角形的高线
1.掌握三角形的高线的概念.(重点)
2.掌握三角形的高线的画法.(难点)
3.了解三角形的重心的概念.
学习目标
新课导入
知识回
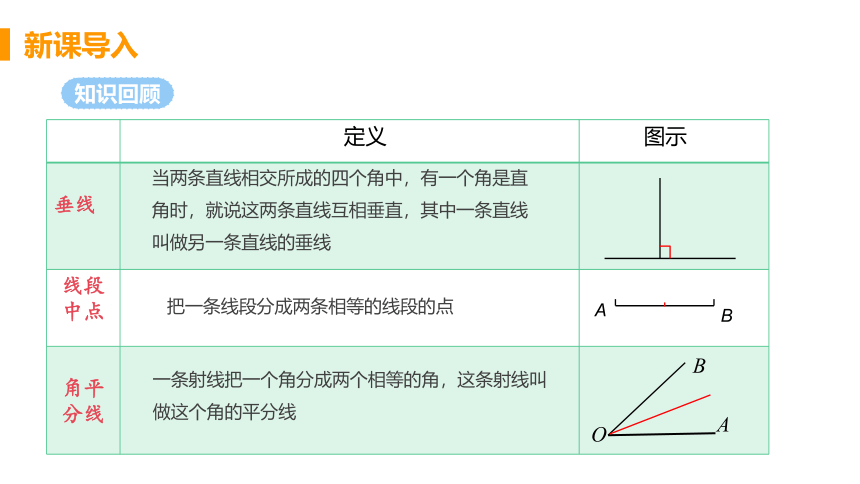
知识回顾
{8799B23B-EC83-4686-B30A-512413B5E67A}
定义
图示
垂线
线段中点
角平分线
当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线
把一条线段分成两条相等的线段的点
A
B
一条射线把一个角分成两个相等的角,这条射线叫做这个角的平分线
O
B
A
新课讲解
知识点1 三角形的稳定性
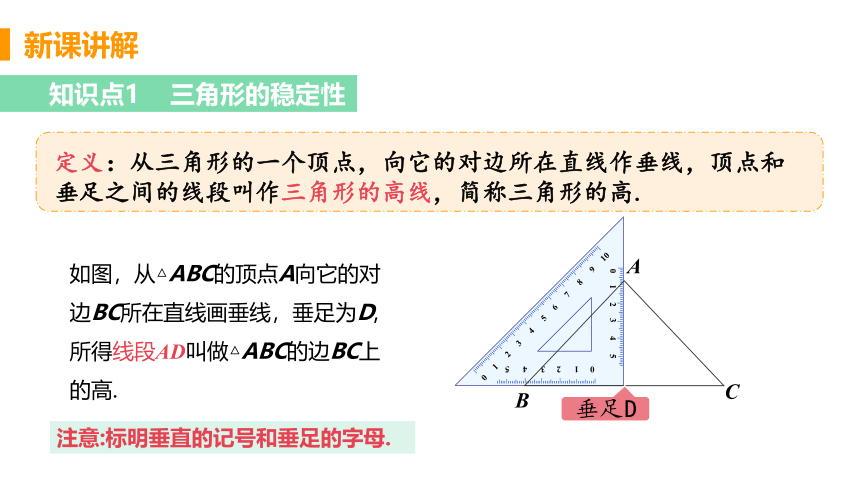
定义:从三角形的一个顶点,向它的对边所在直线作垂线,顶点和垂足之间的线段叫作三角形的高线,简称三角形的高.
如图,从△ABC的顶点A向它的对边BC所在直线画垂线,垂足为D,所得线段AD叫做△ABC的边BC上的高.
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
A
B
C
垂足D
注意:标明垂直的记号和垂足的字母.
新课讲解
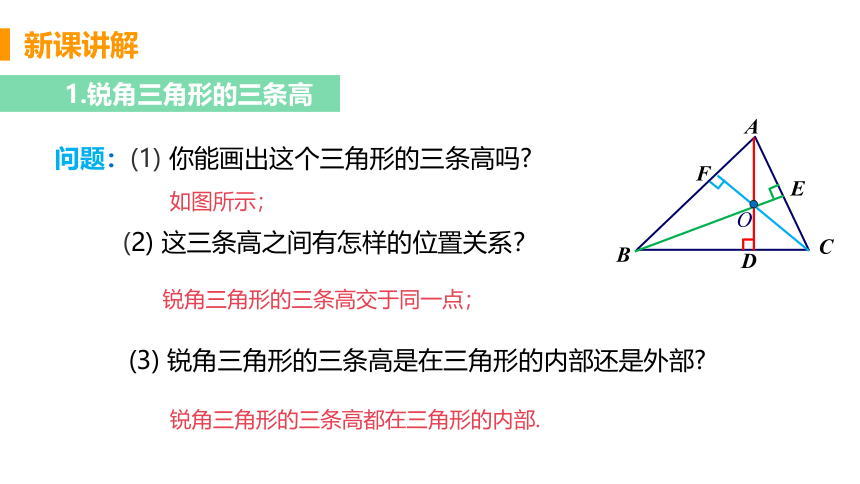
1.锐角三角形的三条高
F
E
A
B
O
C
D
问题:(1) 你能画出这个三角形的三条高吗?
(2) 这三条高之间有怎样的位置关系?
(3) 锐角三角形的三条高是在三角形的内部还是外部?
如图所示;
锐角三角形的三条高交于同一点;
锐角三角形的三条高都在三角形的内部.
新课讲解
2.直角三角形的三条高
问题: 画出直角三角形的三条高,直角三角形的三条高又有怎样的位置关系吗?
直角三角形的三条高交于直角顶点;
A
B
C
D
AC边上的高是 ;
直角边BC边上的高是 ;
直角边AB边上的高是 ;
BD
AB
BC
新课讲解
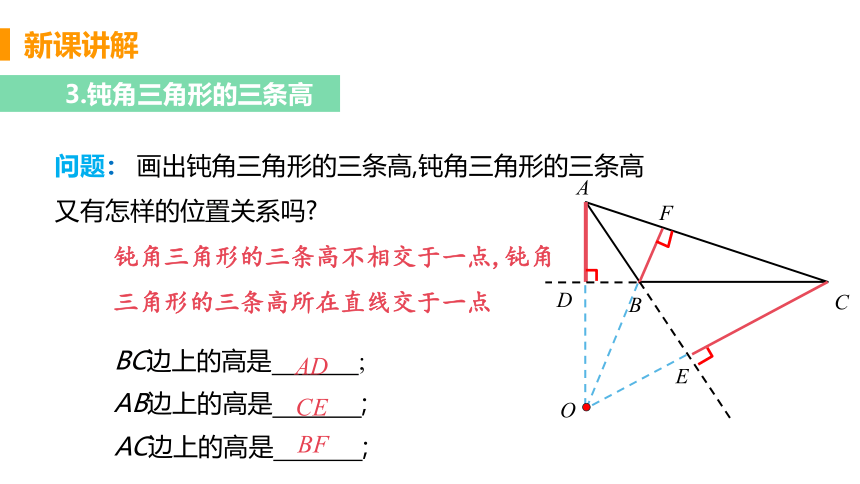
3.钝角三角形的三条高
问题: 画出钝角三角形的三条高,钝角三角形的三条高又有怎样的位置关系吗?
钝角三角形的三条高不相交于一点,钝角三角形的三条高所在直线交于一点
AC边上的高是 ;
BC边上的高是 ;
AB边上的高是 ;
BF
AD
CE
A
B
D
F
O
E
C
新课讲解
要点归纳
新课讲解
例1
典例分析
作△ABC的边AB上的高,下列作法中,正确的是( )
D
方法总结:三角形任意一边上的高必须满足:(1)过该边所对的顶点;(2)垂足必须在该边或在该边的延长线上.
课堂小结
三角形重要线段
三角形的三条角平分线交于三角形内部一点,这一点我们称为三角形的内心
直角三角形:三条高交于直角顶点
锐角三角形:三条高交于在三角形的内部一点
钝角三角形:三条高所在直线交于三角形外部一点
高
中线
三角形的三条中线交于三角形内部一点,这一点我们称为三角形的重心
一边上的中线把原三角形分成两个面积相等的三角形,这两个三角形的周长差等于原三角形其余两边的差
角平分线
当堂小练
1.如图,在△ABC中, ∠1=∠2,G为AD中点,延长BG交 AC于E,F为AB上一点,CF交AD于H,判断下列说法的正误.
(1)AD是△ABE的角平分线( )
(2)BE是△ABD边AD上的中线( )
(3)BE是△ABC边AC上的中线( )
⌒
⌒
A
B
C
D
E
1
2
F
G
H
×
×
解析:(1)AD线段不在△ABE内部,所以不是其角平分线
(2)BE 线段不在△ABD内部,所以不是其角平分线
(3)AE不等于CE,所以BE不是△ABC边AC上的中线
×
当堂小练
?
B
当堂小练
3.如图,AE是 △ABC的角平分线.已知∠B=45°,∠C=60°,求∠BAE和∠AEB的度数.
????
?
????
?
????
?
????
?
D
拓展与延伸
3.如图所示,在等腰三角形ABC 中,AB = AC,一腰上的中线BD 将这个等腰三角形的周长分成12 和6 两部分, 求这个等腰三角形的腰长及底边长.
解:设AB = AC = 2x,则AD = CD = x.
(1)当AB+AD = 12,BC+CD = 6 时,有2x+x = 12,
所以x = 4,2x = 8. 所以AB = AC = 8,BC = 6-4 = 2.
(2)当BC+CD = 12,AB+AD = 6 时,有2x+x = 6,
解得x = 2,所以2x = 4.
所以AB = AC = 4,BC = 12-2 = 10.
因为4+4<10,所以此时不能构成三角形.
综上所述,等腰三角形ABC 的腰长为8,底边长为2.
布置作业
请完成对应习题
1 认识三角形
课时4 三角形的高线
1.掌握三角形的高线的概念.(重点)
2.掌握三角形的高线的画法.(难点)
3.了解三角形的重心的概念.
学习目标
新课导入
知识回
知识回顾
{8799B23B-EC83-4686-B30A-512413B5E67A}
定义
图示
垂线
线段中点
角平分线
当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线
把一条线段分成两条相等的线段的点
A
B
一条射线把一个角分成两个相等的角,这条射线叫做这个角的平分线
O
B
A
新课讲解
知识点1 三角形的稳定性
定义:从三角形的一个顶点,向它的对边所在直线作垂线,顶点和垂足之间的线段叫作三角形的高线,简称三角形的高.
如图,从△ABC的顶点A向它的对边BC所在直线画垂线,垂足为D,所得线段AD叫做△ABC的边BC上的高.
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
A
B
C
垂足D
注意:标明垂直的记号和垂足的字母.
新课讲解
1.锐角三角形的三条高
F
E
A
B
O
C
D
问题:(1) 你能画出这个三角形的三条高吗?
(2) 这三条高之间有怎样的位置关系?
(3) 锐角三角形的三条高是在三角形的内部还是外部?
如图所示;
锐角三角形的三条高交于同一点;
锐角三角形的三条高都在三角形的内部.
新课讲解
2.直角三角形的三条高
问题: 画出直角三角形的三条高,直角三角形的三条高又有怎样的位置关系吗?
直角三角形的三条高交于直角顶点;
A
B
C
D
AC边上的高是 ;
直角边BC边上的高是 ;
直角边AB边上的高是 ;
BD
AB
BC
新课讲解
3.钝角三角形的三条高
问题: 画出钝角三角形的三条高,钝角三角形的三条高又有怎样的位置关系吗?
钝角三角形的三条高不相交于一点,钝角三角形的三条高所在直线交于一点
AC边上的高是 ;
BC边上的高是 ;
AB边上的高是 ;
BF
AD
CE
A
B
D
F
O
E
C
新课讲解
要点归纳
新课讲解
例1
典例分析
作△ABC的边AB上的高,下列作法中,正确的是( )
D
方法总结:三角形任意一边上的高必须满足:(1)过该边所对的顶点;(2)垂足必须在该边或在该边的延长线上.
课堂小结
三角形重要线段
三角形的三条角平分线交于三角形内部一点,这一点我们称为三角形的内心
直角三角形:三条高交于直角顶点
锐角三角形:三条高交于在三角形的内部一点
钝角三角形:三条高所在直线交于三角形外部一点
高
中线
三角形的三条中线交于三角形内部一点,这一点我们称为三角形的重心
一边上的中线把原三角形分成两个面积相等的三角形,这两个三角形的周长差等于原三角形其余两边的差
角平分线
当堂小练
1.如图,在△ABC中, ∠1=∠2,G为AD中点,延长BG交 AC于E,F为AB上一点,CF交AD于H,判断下列说法的正误.
(1)AD是△ABE的角平分线( )
(2)BE是△ABD边AD上的中线( )
(3)BE是△ABC边AC上的中线( )
⌒
⌒
A
B
C
D
E
1
2
F
G
H
×
×
解析:(1)AD线段不在△ABE内部,所以不是其角平分线
(2)BE 线段不在△ABD内部,所以不是其角平分线
(3)AE不等于CE,所以BE不是△ABC边AC上的中线
×
当堂小练
?
B
当堂小练
3.如图,AE是 △ABC的角平分线.已知∠B=45°,∠C=60°,求∠BAE和∠AEB的度数.
????
?
????
?
????
?
????
?
D
拓展与延伸
3.如图所示,在等腰三角形ABC 中,AB = AC,一腰上的中线BD 将这个等腰三角形的周长分成12 和6 两部分, 求这个等腰三角形的腰长及底边长.
解:设AB = AC = 2x,则AD = CD = x.
(1)当AB+AD = 12,BC+CD = 6 时,有2x+x = 12,
所以x = 4,2x = 8. 所以AB = AC = 8,BC = 6-4 = 2.
(2)当BC+CD = 12,AB+AD = 6 时,有2x+x = 6,
解得x = 2,所以2x = 4.
所以AB = AC = 4,BC = 12-2 = 10.
因为4+4<10,所以此时不能构成三角形.
综上所述,等腰三角形ABC 的腰长为8,底边长为2.
布置作业
请完成对应习题
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
