北师大版数学七年级下册4.3.2 用“角边角”“角角边”判定三角形全等 课件(37张)
文档属性
| 名称 | 北师大版数学七年级下册4.3.2 用“角边角”“角角边”判定三角形全等 课件(37张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 986.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-19 00:00:00 | ||
图片预览






文档简介
第四章 三角形
3 探索三角形全等的条件
课时2 用“角边角”“角角边”判定三角形全等
1.理解并掌握三角形全等判定“角边角、角角边”条件的内容.(重点)
2.熟练利用“角边角、角角边”条件证明两个三角形全等.(难点)
3.通过探究判定三角形全等条件的过程,提高分析和解决问题的能力.
学习目标
新课讲解
思考
先任意画出一个△ABC,再画一个△A′B′C′,使得AB=A′B′,∠A=∠A′,∠B=∠B′(即两角和它们的夹边分别相等).此时的△ABC和△A′B′C′全等吗?
画法:1、画A′B′=AB.
2、在A′B′的同旁画∠DA′B′=∠A
∠EB′A′=∠B, A′D,B′E相交于点C′.
3、△A′B′C′即为所作三角形.
通过画图,你能得出什么样的结论?
新课讲解
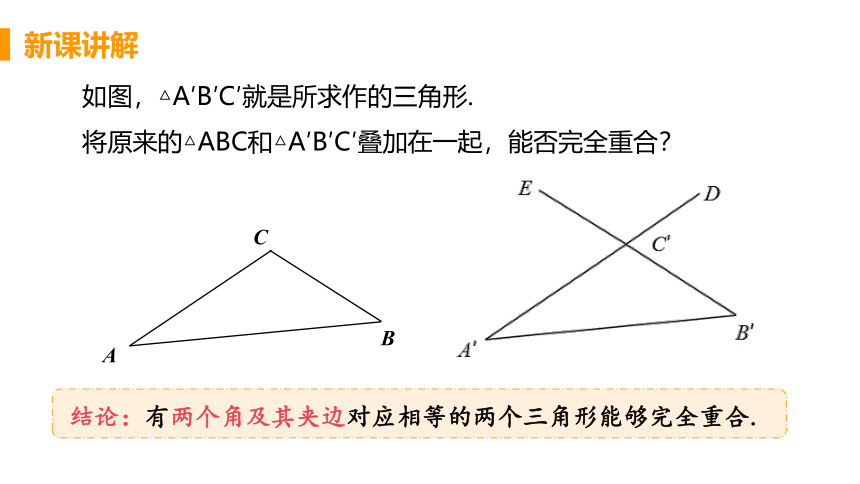
如图,△A′B′C′就是所求作的三角形.
将原来的△ABC和△A′B′C′叠加在一起,能否完全重合?
C
A
B
结论:有两个角及其夹边对应相等的两个三角形能够完全重合.
新课讲解
知识点1 全等形的判定3
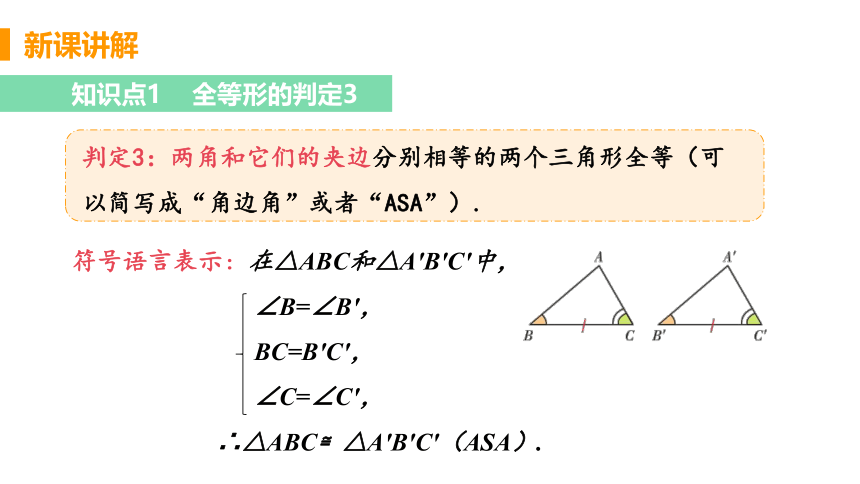
判定3:两角和它们的夹边分别相等的两个三角形全等(可以简写成“角边角”或者“ASA”).
符号语言表示:在△ABC和△A′B′C′中,
∠B=∠B′,
BC=B′C′,
∠C=∠C′,
∴△ABC≌△A′B′C′(ASA).
新课讲解
例
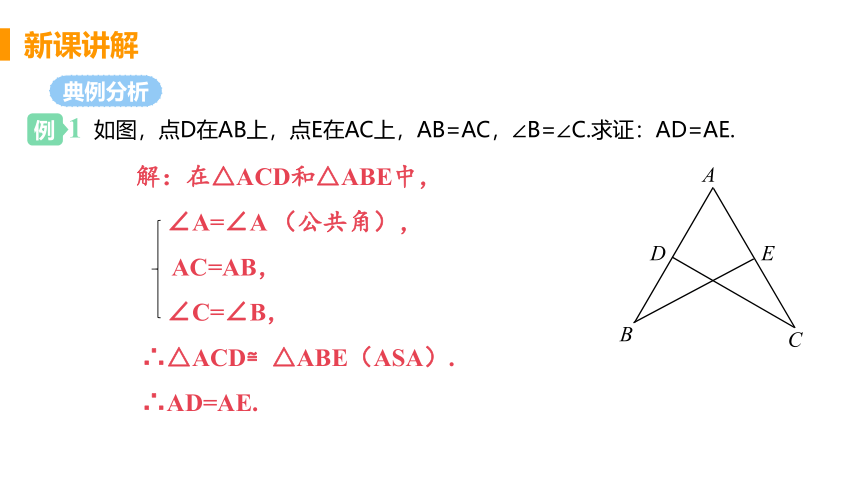
1 如图,点D在AB上,点E在AC上,AB=AC,∠B=∠C.求证:AD=AE.
典例分析
D
E
B
C
A
解:在△ACD和△ABE中,
∠A=∠A (公共角),
AC=AB,
∠C=∠B,
∴△ACD≌△ABE(ASA).
∴AD=AE.
新课讲解
例
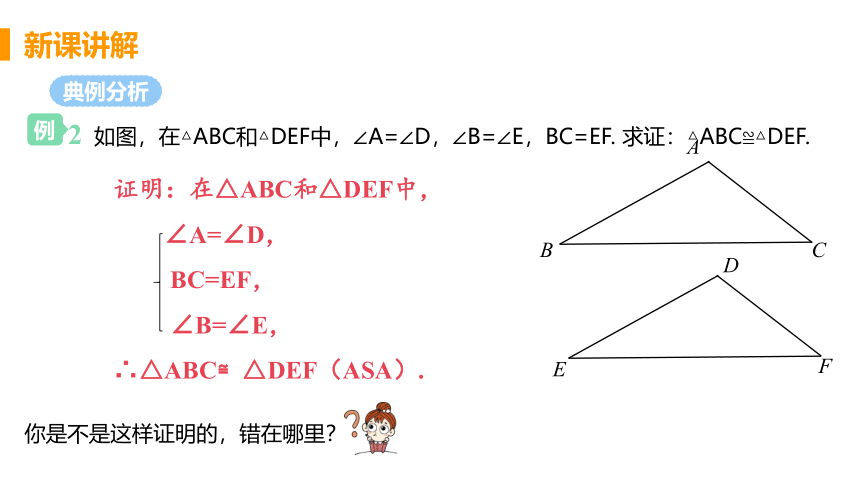
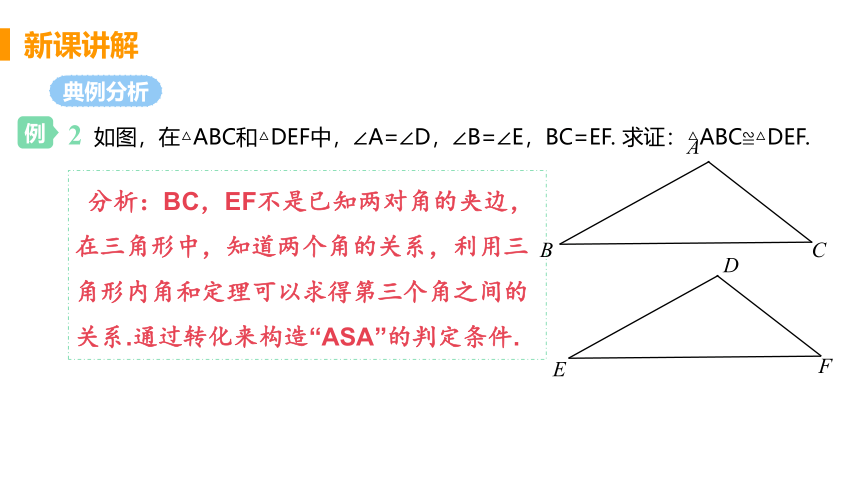
2 如图,在△ABC和△DEF中,∠A=∠D,∠B=∠E,BC=EF. 求证:△ABC≌△DEF.
典例分析
证明:在△ABC和△DEF中,
∠A=∠D,
BC=EF,
∠B=∠E,
∴△ABC≌△DEF(ASA).
A
B
E
D
C
F
你是不是这样证明的,错在哪里?
新课讲解
例
2 如图,在△ABC和△DEF中,∠A=∠D,∠B=∠E,BC=EF. 求证:△ABC≌△DEF.
典例分析
分析:BC,EF不是已知两对角的夹边,在三角形中,知道两个角的关系,利用三角形内角和定理可以求得第三个角之间的关系.通过转化来构造“ASA”的判定条件.
A
B
E
D
C
F
新课讲解
例
如图,在△ABC和△DEF中,∠A=∠D,∠B=∠E,BC=EF. 求证:△ABC≌△DEF.
证明:在△ABC和△DEF中,
∵∠A=∠D,∠B=∠E,
∠C=180°-∠A-∠B,∠F=180°-∠D-∠E,
∴∠C=∠F.
在△ABC和△DEF中,
∠B=∠E,
BC=EF,
∠C=∠F,
∴△ABC≌△DEF(ASA).
A
B
E
D
C
F
新课讲解
如图,AB⊥BC,AD⊥DC,垂足分别为点B,点D,∠1=∠2.
求证:AB=AD.
练一练
分析:图中的两个三角形有公共边AC,有一对角相等可以选择“SAS”或者“ASA”.根据题意,有AB⊥BC,AD⊥DC,则构成∠ABC=∠ADC=90°.可以选择“ASA”,需要将已知角转化成两角及其夹边,即可求证.
A
B
C
D
1
2
新课讲解
如图,AB⊥BC,AD⊥DC,垂足分别为点B,点D,∠1=∠2.
求证:AB=AD.
练一练
A
B
C
D
1
2
证明:∵AB⊥BC,AD⊥DC, ∴∠ABC=∠ADC=90°.
∵在△ABC和△ADC中,∠1=∠2,∠ABC=∠ADC,
∴∠ACB=∠ACD.
在△ABC和△ADC中,
∠1=∠2,
AC=AC(公共边),
∠ACB=∠ACD,
∴△ABC≌△ADC(ASA), ∴AB=AD.
新课讲解
练一练
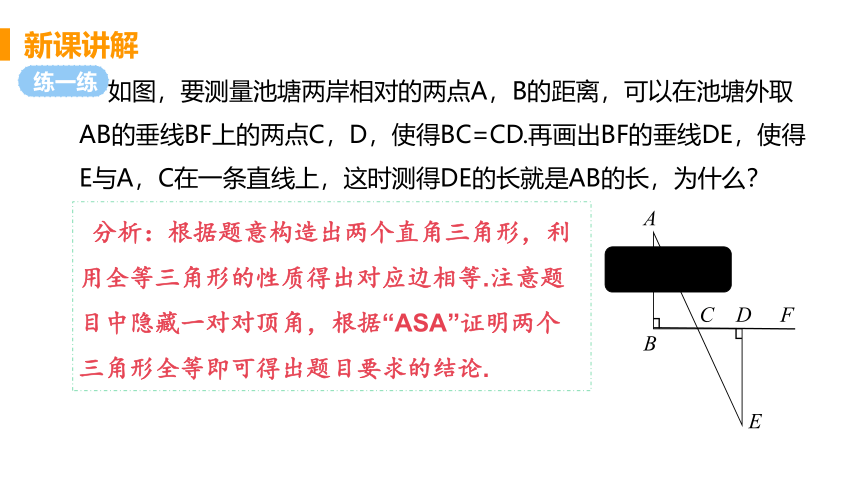
如图,要测量池塘两岸相对的两点A,B的距离,可以在池塘外取AB的垂线BF上的两点C,D,使得BC=CD.再画出BF的垂线DE,使得E与A,C在一条直线上,这时测得DE的长就是AB的长,为什么?
A
B
C
D
F
E
┐
┐
分析:根据题意构造出两个直角三角形,利用全等三角形的性质得出对应边相等.注意题目中隐藏一对对顶角,根据“ASA”证明两个三角形全等即可得出题目要求的结论.
新课讲解
练一练
如图,要测量池塘两岸相对的两点A,B的距离,可以在池塘外取AB的垂线BF上的两点C,D,使得BC=CD.再画出BF的垂线DE,使得E与A,C在一条直线上,这时测得DE的长就是AB的长,为什么?
A
B
C
D
F
E
┐
┐
解:由题可知:AB⊥BC,ED⊥DC,
则∠ABC=∠EDC=90°.
在△ABC和△EDC中,
∠ABC=∠EDC,
BC=DC,
∠ACB=∠ECD,
∴△ABC≌△EDC(ASA).
∴AB=ED,则DE的长就是AB的长.
新课讲解
练一练
如下图,已知∠B=∠D,DC=BC,还需要给出什么条件,即可用学过的判定得出△ABC≌△EDC.根据哪个判定?
C
E
A
D
B
(1)条件( ),
根据( ).
(2)条件( ),
根据( ).
AB=ED
两边及其夹角分别相等的两个三角形全等
∠ACB=∠ECD
两角及其夹边分别相等的两个三角形全等
新课讲解
思考
两角分别相等且其中一组等角的对边相等,这样的两个三角形全等吗?
在△ABC和△A'B'C'中,使得AB=A'B',∠C=∠C',∠B=∠B'.
此时的△ABC和△A'B'C'全等吗?
A
B
B'
A'
C
C'
请选用已经学过的全等三角形的判定来证明△ABC和△A'B'C'全等.
新课讲解
已知,在△ABC和△A′B′C′中,AB=A′B′,∠C=∠C′,∠B=∠B′.
证明△ABC≌△A′B′C′.?
A
B
B'
A'
C
C'
证明:∵∠C=∠C′,∠B=∠B′,
∠A=180°-∠B-∠C,
∠A′=180°-∠B′-∠C′,
∴∠A=∠A′.
在△ABC和△A′B′C′中,
∠A=∠A′,
AB=A′B′,
∠B=∠B′,
∴△ABC≌△A′B′C′(ASA).
新课讲解
知识点1 全等形的判定4
判定4:两角分别相等且其中一组等角的对边相等的两个三角形全等.(可以简写成“角角边”或者“AAS”).
符号语言表示:在△ABC和△A′B′C′中,
∠A=∠A′,
∠B=∠B′,
BC=B′C′,
∴△ABC≌△A′B′C′(AAS).
要按照”角—角—边“的顺序书写.
新课讲解
例
1 如图,在△ABC和△ADC中,∠B=∠D=90°,∠BAC=∠DAC.
求证:△ABC≌△ADC.
典例分析
解:在△ABC和△ADC中,
∠B=∠D,
∠BAC=∠DAC,
AC=AC(公共边),
∴△ABC≌△ADC(AAS).
┐
A
B
D
C
┐
新课讲解
如图,BE=CD,∠1=∠2,则AB=AC吗?为什么?
练一练
分析: 利用三角形全等的性质说明AB=AC.
AB,AC分别在△AEB和△ADC中, 则需要证明△AEB≌△ADC.题目中已有一边和两角相等,可以考虑选择 “ASA”或者“AAS”,将∠1=∠2转化成△AEB 和△ADC中相等的角即可.
1
B
D
A
E
2
新课讲解
如图,BE=CD,∠1=∠2,则AB=AC吗?为什么?
练一练
1
B
D
A
E
2
证明:∵∠2是△AEB的外角,∴∠AEB=180°-∠2.
∵∠1是△ADC的外角,∴∠ADC=180°-∠1.
∵∠1=∠2,∴ ∠AEB=∠ADC.
在△AEB和△ADC中, ∠A=∠A
∠AEB=∠ADC,
BE=CD,
∴△AEB≌△ADC(AAS). ∴AB=AC.
新课讲解
如果两个三角形中,有两个角和一条边分别相等,那么这两个三角形是全等三角形.
有两个角和一条边分别对应相等的两个三角形是否一定全等?
思考
思考
“ASA”和“AAS”之间有什么关系?
在证明两个三角形全等过程中,“ASA”和“AAS”两个判定是可以相互转化的.
你能总结一下“ASA”和“AAS”的区别与联系吗?
新课讲解
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}ASA
“ASA”和'AAS”的区别与联系
“S”的意义
书写格式
联系
ASA
“S”是两角的夹边
把夹边相等写在两角相等的中间
由三角形的内角和定理可知,“ASA”和“AAS”可以互相转化
AAS
“S”是其中一角的对边
把两角相等写在一起,边相等放在最后
新课讲解
练一练
如图,点O是AB的中点,∠C=∠D,则△AOC和△BOD全等吗?请用两种方法证明.
B
A
O
D
C
解:△AOC和△BOD全等,理由如下:
∵点O是AB的中点, ∴OA=OB.
∵在△AOC和△BOD中,∠C=∠D,∠AOC=∠BOD,
∴∠A=∠B(三角形内角和定理).
在△AOC和△BOD中, ∠A=∠B,
OA=OB,
∠AOC=∠BOD,
∴△AOC≌△BOD(ASA).
新课讲解
练一练
如图,点O是AB的中点,∠C=∠D,则△AOC和△BOD全等吗?请用两种方法证明.
B
A
O
D
C
解:△AOC和△BOD全等,理由如下:
∵点O是AB的中点, ∴OA=OB.
∵在△AOC和△BOD中, ∠C=∠D,
∠AOC=∠BOD,
OA=OB,
∴△AOC≌△BOD(AAS).
新课讲解
练一练
已知,如图,点E是AC上一点,AB=CE,AB//CD,∠ACB=∠D.
求证:BC=ED.
证明:∵AB//CD, ∴∠A=∠ECD.
在△ACB和△CDE中,
∠ACB=∠D,
∠A=∠ECD,
AB=CE,
∴△ACB≌△CDE(AAS).
∴BC=ED.
A
B
E
C
D
课堂小结
两角和它们的夹边分别相等的两个三角形全等
ASA
应用
利用“ASA、AAS”解决实际问题
分类探讨
两角及其夹边分别相等
两角及其中一角的对边分别相等
三角形全等的判定
AAS
两角和其中一组角的对边分别相等的两个三角形全等
对比探究
对比“ASA”和“AAS”的区别和联系
当堂小练
如图,已知∠1=∠2,∠C=∠D.求证:AC=AD.
证明:∵∠1=∠2,∠C=∠D,
∴∠ABC=∠ABD (三角形内角和定理).
在△ABC和△ABD中,
∠1=∠2,
AB=AB(公共边),
∠ABC=∠ABD,
∴△ABC≌△ABD(ASA).
∴AC=AD.
A
B
1
2
C
D
当堂小练
如图,已知D是AC上一点,AB=DA,DE//AB,∠B=∠DAE.
求证:△ABC≌△DAE.
证明:∵DE//AB, ∴ ∠CAB=∠EDA.
在△ABC和△DAE中,
∠CAB=∠EDA,
AB=DA,
∠B=∠DAE,
∴△ABC≌△DAE(ASA).
为你支招:有平行线就可以转化出相等的角.
当堂小练
如图,在Rt△ABC中,∠ACB=90°,BC=2cm,CD⊥AB,在AC上取一点E,使EC=BC,过点E作EF⊥AC交CD的延长线于点F,如果EF=5cm,那么AE=( )cm.
分析:题目中已经给出一对边相等,可以选择“SSS”,“SAS”或者“ASA”.根据题意的垂直关系可以转化出相等的角,所以本题选择“ASA”.
利用好垂直关系和余角定理是解决本题的关键.
当堂小练
如图,在Rt△ABC中,∠ACB=90°,BC=2cm,CD⊥AB,在AC上取一点E,使EC=BC,过点E作EF⊥AC交CD的延长线于点F,如果EF=5cm,那么AE=( )cm.
3
解:∵CD⊥AB, ∴∠A+∠ACD=90°.
∵∠ACB=90°,∴∠A+∠B=90°. ∴∠B=∠ACD.
∵EF⊥AC, ∴∠FEC=90°. ∴∠ACB=∠FEC.
在△ACB和△FEC中,∠B=∠FCE,
BC=CE,
∠ACB=∠FEC,
∴△ACB≌△FEC(ASA). ∴ AC=EF.
∵BC=2cm,EF=5cm. ∴ AE=3cm.
当堂小练
如图,已知点B,E,C,F在同一直线上,AB=DE,∠A=∠D,AC//DF.
求证:(1)△ABC≌△DEF.(2)BE=CF.
证明:(1)∵AC//DF, ∴∠ACB=∠F.
在△ABC和△DEF中,
∠ACB=∠F,
∠A=∠D,
AB=DE,
∴△ABC≌△DEF(AAS).
A
C
D
F
B
E
(2)∵△ABC≌△DEF, ∴BC=EF.∴BC-EC=EF-EC,即BE=CF.
等边加(减)等边,其和(差)还是等边,等角加(减)等角,其和(差)还是等角.
D
拓展与延伸
如图,已知∠1=∠2,∠E=∠C,AC=AE.求证:AB=AD,∠B=∠D.
1
B
E
D
A
2
分析:等角加等角,其和仍然是等角;同理,等角减等角,其差仍然是等角.利用题目中已经给出的角转化出新的相等的角,从而证明三角形全等,利用全等的性质得出对应角相等,对应边相等.
D
拓展与延伸
如图,已知∠1=∠2,∠E=∠C,AC=AE.求证:AB=AD,∠B=∠D.
1
B
E
D
A
2
证明:∵∠1=∠2,
∴∠1+∠EAC=∠2+∠EAC,即∠BAC=∠DAE.
在△ABC和△ADE中,
∠BAC=∠DAE,
AC=AE,
∠C=∠E,
∴△ABC≌△ADE(ASA).
∴AB=AD,∠B=∠D.
D
拓展与延伸
如图,已知AD是∠BAC的平分线,在不添加任何辅助线的前提下,要△AED≌△AFD,可添加一个什么条件?并给予证明.
已有一边和一角分别相等,可以构造一边相等选择“SAS”.
解:(1) 添加AE=AF,证明如下:
∵AD是∠BAC的平分线, ∴∠EAD=∠FAD.
∵在△AED和△AFD中,AE=AF,
∠EAD=∠FAD,
AD=AD,
∴△AED≌△AFD(SAS).
D
拓展与延伸
如图,已知AD是∠BAC的平分线,在不添加任何辅助线的前提下,要△AED≌△AFD,可添加一个什么条件?并给予证明.
解:(2) 添加∠EDA=∠FDA ,证明如下:
∵AD是∠BAC的平分线, ∴∠EAD=∠FAD.
∵在△AED和△AFD中,∠EDA=∠FDA,
AD=AD,
∠EAD=∠FAD,
∴△AED≌△AFD(ASA).
已有一边和一角分别相等,可以构造一角相等选择“ASA”.
D
拓展与延伸
如图,已知AD是∠BAC的平分线,在不添加任何辅助线的前提下,要△AED≌△AFD,可添加一个什么条件?并给予证明.
解:(3) 添加∠DEA=∠DFA,证明如下:
∵AD是∠BAC的平分线, ∴∠EAD=∠FAD.
∵在△AED和△AFD中,∠DEA=∠DFA,
∠EAD=∠FAD,
AD=AD,
∴△AED≌△AFD(AAS).
已有一边和一角分别相等,可以构造一边相等选择“AAS”.
布置作业
请完成对应习题
3 探索三角形全等的条件
课时2 用“角边角”“角角边”判定三角形全等
1.理解并掌握三角形全等判定“角边角、角角边”条件的内容.(重点)
2.熟练利用“角边角、角角边”条件证明两个三角形全等.(难点)
3.通过探究判定三角形全等条件的过程,提高分析和解决问题的能力.
学习目标
新课讲解
思考
先任意画出一个△ABC,再画一个△A′B′C′,使得AB=A′B′,∠A=∠A′,∠B=∠B′(即两角和它们的夹边分别相等).此时的△ABC和△A′B′C′全等吗?
画法:1、画A′B′=AB.
2、在A′B′的同旁画∠DA′B′=∠A
∠EB′A′=∠B, A′D,B′E相交于点C′.
3、△A′B′C′即为所作三角形.
通过画图,你能得出什么样的结论?
新课讲解
如图,△A′B′C′就是所求作的三角形.
将原来的△ABC和△A′B′C′叠加在一起,能否完全重合?
C
A
B
结论:有两个角及其夹边对应相等的两个三角形能够完全重合.
新课讲解
知识点1 全等形的判定3
判定3:两角和它们的夹边分别相等的两个三角形全等(可以简写成“角边角”或者“ASA”).
符号语言表示:在△ABC和△A′B′C′中,
∠B=∠B′,
BC=B′C′,
∠C=∠C′,
∴△ABC≌△A′B′C′(ASA).
新课讲解
例
1 如图,点D在AB上,点E在AC上,AB=AC,∠B=∠C.求证:AD=AE.
典例分析
D
E
B
C
A
解:在△ACD和△ABE中,
∠A=∠A (公共角),
AC=AB,
∠C=∠B,
∴△ACD≌△ABE(ASA).
∴AD=AE.
新课讲解
例
2 如图,在△ABC和△DEF中,∠A=∠D,∠B=∠E,BC=EF. 求证:△ABC≌△DEF.
典例分析
证明:在△ABC和△DEF中,
∠A=∠D,
BC=EF,
∠B=∠E,
∴△ABC≌△DEF(ASA).
A
B
E
D
C
F
你是不是这样证明的,错在哪里?
新课讲解
例
2 如图,在△ABC和△DEF中,∠A=∠D,∠B=∠E,BC=EF. 求证:△ABC≌△DEF.
典例分析
分析:BC,EF不是已知两对角的夹边,在三角形中,知道两个角的关系,利用三角形内角和定理可以求得第三个角之间的关系.通过转化来构造“ASA”的判定条件.
A
B
E
D
C
F
新课讲解
例
如图,在△ABC和△DEF中,∠A=∠D,∠B=∠E,BC=EF. 求证:△ABC≌△DEF.
证明:在△ABC和△DEF中,
∵∠A=∠D,∠B=∠E,
∠C=180°-∠A-∠B,∠F=180°-∠D-∠E,
∴∠C=∠F.
在△ABC和△DEF中,
∠B=∠E,
BC=EF,
∠C=∠F,
∴△ABC≌△DEF(ASA).
A
B
E
D
C
F
新课讲解
如图,AB⊥BC,AD⊥DC,垂足分别为点B,点D,∠1=∠2.
求证:AB=AD.
练一练
分析:图中的两个三角形有公共边AC,有一对角相等可以选择“SAS”或者“ASA”.根据题意,有AB⊥BC,AD⊥DC,则构成∠ABC=∠ADC=90°.可以选择“ASA”,需要将已知角转化成两角及其夹边,即可求证.
A
B
C
D
1
2
新课讲解
如图,AB⊥BC,AD⊥DC,垂足分别为点B,点D,∠1=∠2.
求证:AB=AD.
练一练
A
B
C
D
1
2
证明:∵AB⊥BC,AD⊥DC, ∴∠ABC=∠ADC=90°.
∵在△ABC和△ADC中,∠1=∠2,∠ABC=∠ADC,
∴∠ACB=∠ACD.
在△ABC和△ADC中,
∠1=∠2,
AC=AC(公共边),
∠ACB=∠ACD,
∴△ABC≌△ADC(ASA), ∴AB=AD.
新课讲解
练一练
如图,要测量池塘两岸相对的两点A,B的距离,可以在池塘外取AB的垂线BF上的两点C,D,使得BC=CD.再画出BF的垂线DE,使得E与A,C在一条直线上,这时测得DE的长就是AB的长,为什么?
A
B
C
D
F
E
┐
┐
分析:根据题意构造出两个直角三角形,利用全等三角形的性质得出对应边相等.注意题目中隐藏一对对顶角,根据“ASA”证明两个三角形全等即可得出题目要求的结论.
新课讲解
练一练
如图,要测量池塘两岸相对的两点A,B的距离,可以在池塘外取AB的垂线BF上的两点C,D,使得BC=CD.再画出BF的垂线DE,使得E与A,C在一条直线上,这时测得DE的长就是AB的长,为什么?
A
B
C
D
F
E
┐
┐
解:由题可知:AB⊥BC,ED⊥DC,
则∠ABC=∠EDC=90°.
在△ABC和△EDC中,
∠ABC=∠EDC,
BC=DC,
∠ACB=∠ECD,
∴△ABC≌△EDC(ASA).
∴AB=ED,则DE的长就是AB的长.
新课讲解
练一练
如下图,已知∠B=∠D,DC=BC,还需要给出什么条件,即可用学过的判定得出△ABC≌△EDC.根据哪个判定?
C
E
A
D
B
(1)条件( ),
根据( ).
(2)条件( ),
根据( ).
AB=ED
两边及其夹角分别相等的两个三角形全等
∠ACB=∠ECD
两角及其夹边分别相等的两个三角形全等
新课讲解
思考
两角分别相等且其中一组等角的对边相等,这样的两个三角形全等吗?
在△ABC和△A'B'C'中,使得AB=A'B',∠C=∠C',∠B=∠B'.
此时的△ABC和△A'B'C'全等吗?
A
B
B'
A'
C
C'
请选用已经学过的全等三角形的判定来证明△ABC和△A'B'C'全等.
新课讲解
已知,在△ABC和△A′B′C′中,AB=A′B′,∠C=∠C′,∠B=∠B′.
证明△ABC≌△A′B′C′.?
A
B
B'
A'
C
C'
证明:∵∠C=∠C′,∠B=∠B′,
∠A=180°-∠B-∠C,
∠A′=180°-∠B′-∠C′,
∴∠A=∠A′.
在△ABC和△A′B′C′中,
∠A=∠A′,
AB=A′B′,
∠B=∠B′,
∴△ABC≌△A′B′C′(ASA).
新课讲解
知识点1 全等形的判定4
判定4:两角分别相等且其中一组等角的对边相等的两个三角形全等.(可以简写成“角角边”或者“AAS”).
符号语言表示:在△ABC和△A′B′C′中,
∠A=∠A′,
∠B=∠B′,
BC=B′C′,
∴△ABC≌△A′B′C′(AAS).
要按照”角—角—边“的顺序书写.
新课讲解
例
1 如图,在△ABC和△ADC中,∠B=∠D=90°,∠BAC=∠DAC.
求证:△ABC≌△ADC.
典例分析
解:在△ABC和△ADC中,
∠B=∠D,
∠BAC=∠DAC,
AC=AC(公共边),
∴△ABC≌△ADC(AAS).
┐
A
B
D
C
┐
新课讲解
如图,BE=CD,∠1=∠2,则AB=AC吗?为什么?
练一练
分析: 利用三角形全等的性质说明AB=AC.
AB,AC分别在△AEB和△ADC中, 则需要证明△AEB≌△ADC.题目中已有一边和两角相等,可以考虑选择 “ASA”或者“AAS”,将∠1=∠2转化成△AEB 和△ADC中相等的角即可.
1
B
D
A
E
2
新课讲解
如图,BE=CD,∠1=∠2,则AB=AC吗?为什么?
练一练
1
B
D
A
E
2
证明:∵∠2是△AEB的外角,∴∠AEB=180°-∠2.
∵∠1是△ADC的外角,∴∠ADC=180°-∠1.
∵∠1=∠2,∴ ∠AEB=∠ADC.
在△AEB和△ADC中, ∠A=∠A
∠AEB=∠ADC,
BE=CD,
∴△AEB≌△ADC(AAS). ∴AB=AC.
新课讲解
如果两个三角形中,有两个角和一条边分别相等,那么这两个三角形是全等三角形.
有两个角和一条边分别对应相等的两个三角形是否一定全等?
思考
思考
“ASA”和“AAS”之间有什么关系?
在证明两个三角形全等过程中,“ASA”和“AAS”两个判定是可以相互转化的.
你能总结一下“ASA”和“AAS”的区别与联系吗?
新课讲解
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}ASA
“ASA”和'AAS”的区别与联系
“S”的意义
书写格式
联系
ASA
“S”是两角的夹边
把夹边相等写在两角相等的中间
由三角形的内角和定理可知,“ASA”和“AAS”可以互相转化
AAS
“S”是其中一角的对边
把两角相等写在一起,边相等放在最后
新课讲解
练一练
如图,点O是AB的中点,∠C=∠D,则△AOC和△BOD全等吗?请用两种方法证明.
B
A
O
D
C
解:△AOC和△BOD全等,理由如下:
∵点O是AB的中点, ∴OA=OB.
∵在△AOC和△BOD中,∠C=∠D,∠AOC=∠BOD,
∴∠A=∠B(三角形内角和定理).
在△AOC和△BOD中, ∠A=∠B,
OA=OB,
∠AOC=∠BOD,
∴△AOC≌△BOD(ASA).
新课讲解
练一练
如图,点O是AB的中点,∠C=∠D,则△AOC和△BOD全等吗?请用两种方法证明.
B
A
O
D
C
解:△AOC和△BOD全等,理由如下:
∵点O是AB的中点, ∴OA=OB.
∵在△AOC和△BOD中, ∠C=∠D,
∠AOC=∠BOD,
OA=OB,
∴△AOC≌△BOD(AAS).
新课讲解
练一练
已知,如图,点E是AC上一点,AB=CE,AB//CD,∠ACB=∠D.
求证:BC=ED.
证明:∵AB//CD, ∴∠A=∠ECD.
在△ACB和△CDE中,
∠ACB=∠D,
∠A=∠ECD,
AB=CE,
∴△ACB≌△CDE(AAS).
∴BC=ED.
A
B
E
C
D
课堂小结
两角和它们的夹边分别相等的两个三角形全等
ASA
应用
利用“ASA、AAS”解决实际问题
分类探讨
两角及其夹边分别相等
两角及其中一角的对边分别相等
三角形全等的判定
AAS
两角和其中一组角的对边分别相等的两个三角形全等
对比探究
对比“ASA”和“AAS”的区别和联系
当堂小练
如图,已知∠1=∠2,∠C=∠D.求证:AC=AD.
证明:∵∠1=∠2,∠C=∠D,
∴∠ABC=∠ABD (三角形内角和定理).
在△ABC和△ABD中,
∠1=∠2,
AB=AB(公共边),
∠ABC=∠ABD,
∴△ABC≌△ABD(ASA).
∴AC=AD.
A
B
1
2
C
D
当堂小练
如图,已知D是AC上一点,AB=DA,DE//AB,∠B=∠DAE.
求证:△ABC≌△DAE.
证明:∵DE//AB, ∴ ∠CAB=∠EDA.
在△ABC和△DAE中,
∠CAB=∠EDA,
AB=DA,
∠B=∠DAE,
∴△ABC≌△DAE(ASA).
为你支招:有平行线就可以转化出相等的角.
当堂小练
如图,在Rt△ABC中,∠ACB=90°,BC=2cm,CD⊥AB,在AC上取一点E,使EC=BC,过点E作EF⊥AC交CD的延长线于点F,如果EF=5cm,那么AE=( )cm.
分析:题目中已经给出一对边相等,可以选择“SSS”,“SAS”或者“ASA”.根据题意的垂直关系可以转化出相等的角,所以本题选择“ASA”.
利用好垂直关系和余角定理是解决本题的关键.
当堂小练
如图,在Rt△ABC中,∠ACB=90°,BC=2cm,CD⊥AB,在AC上取一点E,使EC=BC,过点E作EF⊥AC交CD的延长线于点F,如果EF=5cm,那么AE=( )cm.
3
解:∵CD⊥AB, ∴∠A+∠ACD=90°.
∵∠ACB=90°,∴∠A+∠B=90°. ∴∠B=∠ACD.
∵EF⊥AC, ∴∠FEC=90°. ∴∠ACB=∠FEC.
在△ACB和△FEC中,∠B=∠FCE,
BC=CE,
∠ACB=∠FEC,
∴△ACB≌△FEC(ASA). ∴ AC=EF.
∵BC=2cm,EF=5cm. ∴ AE=3cm.
当堂小练
如图,已知点B,E,C,F在同一直线上,AB=DE,∠A=∠D,AC//DF.
求证:(1)△ABC≌△DEF.(2)BE=CF.
证明:(1)∵AC//DF, ∴∠ACB=∠F.
在△ABC和△DEF中,
∠ACB=∠F,
∠A=∠D,
AB=DE,
∴△ABC≌△DEF(AAS).
A
C
D
F
B
E
(2)∵△ABC≌△DEF, ∴BC=EF.∴BC-EC=EF-EC,即BE=CF.
等边加(减)等边,其和(差)还是等边,等角加(减)等角,其和(差)还是等角.
D
拓展与延伸
如图,已知∠1=∠2,∠E=∠C,AC=AE.求证:AB=AD,∠B=∠D.
1
B
E
D
A
2
分析:等角加等角,其和仍然是等角;同理,等角减等角,其差仍然是等角.利用题目中已经给出的角转化出新的相等的角,从而证明三角形全等,利用全等的性质得出对应角相等,对应边相等.
D
拓展与延伸
如图,已知∠1=∠2,∠E=∠C,AC=AE.求证:AB=AD,∠B=∠D.
1
B
E
D
A
2
证明:∵∠1=∠2,
∴∠1+∠EAC=∠2+∠EAC,即∠BAC=∠DAE.
在△ABC和△ADE中,
∠BAC=∠DAE,
AC=AE,
∠C=∠E,
∴△ABC≌△ADE(ASA).
∴AB=AD,∠B=∠D.
D
拓展与延伸
如图,已知AD是∠BAC的平分线,在不添加任何辅助线的前提下,要△AED≌△AFD,可添加一个什么条件?并给予证明.
已有一边和一角分别相等,可以构造一边相等选择“SAS”.
解:(1) 添加AE=AF,证明如下:
∵AD是∠BAC的平分线, ∴∠EAD=∠FAD.
∵在△AED和△AFD中,AE=AF,
∠EAD=∠FAD,
AD=AD,
∴△AED≌△AFD(SAS).
D
拓展与延伸
如图,已知AD是∠BAC的平分线,在不添加任何辅助线的前提下,要△AED≌△AFD,可添加一个什么条件?并给予证明.
解:(2) 添加∠EDA=∠FDA ,证明如下:
∵AD是∠BAC的平分线, ∴∠EAD=∠FAD.
∵在△AED和△AFD中,∠EDA=∠FDA,
AD=AD,
∠EAD=∠FAD,
∴△AED≌△AFD(ASA).
已有一边和一角分别相等,可以构造一角相等选择“ASA”.
D
拓展与延伸
如图,已知AD是∠BAC的平分线,在不添加任何辅助线的前提下,要△AED≌△AFD,可添加一个什么条件?并给予证明.
解:(3) 添加∠DEA=∠DFA,证明如下:
∵AD是∠BAC的平分线, ∴∠EAD=∠FAD.
∵在△AED和△AFD中,∠DEA=∠DFA,
∠EAD=∠FAD,
AD=AD,
∴△AED≌△AFD(AAS).
已有一边和一角分别相等,可以构造一边相等选择“AAS”.
布置作业
请完成对应习题
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
