沪科版(2012)初中数学九年级下册 24.4.2直线与圆的位置关系——切线的判定 教案
文档属性
| 名称 | 沪科版(2012)初中数学九年级下册 24.4.2直线与圆的位置关系——切线的判定 教案 |
|
|
| 格式 | zip | ||
| 文件大小 | 78.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-20 00:00:00 | ||
图片预览

文档简介
24.4直线与圆的位置关系——切线的判定学习任务单
学习目标:
1、理解和掌握切线的判定定理,掌握切线的几种判定方法;
2、通过练习,学会运用切线的判定定理进行简单的推理。
学习任务一:复习回顾
1、如何判断一条直线是圆的切线?
方法一:定义;
方法二:比较圆心到直线的距离与半径的关系。
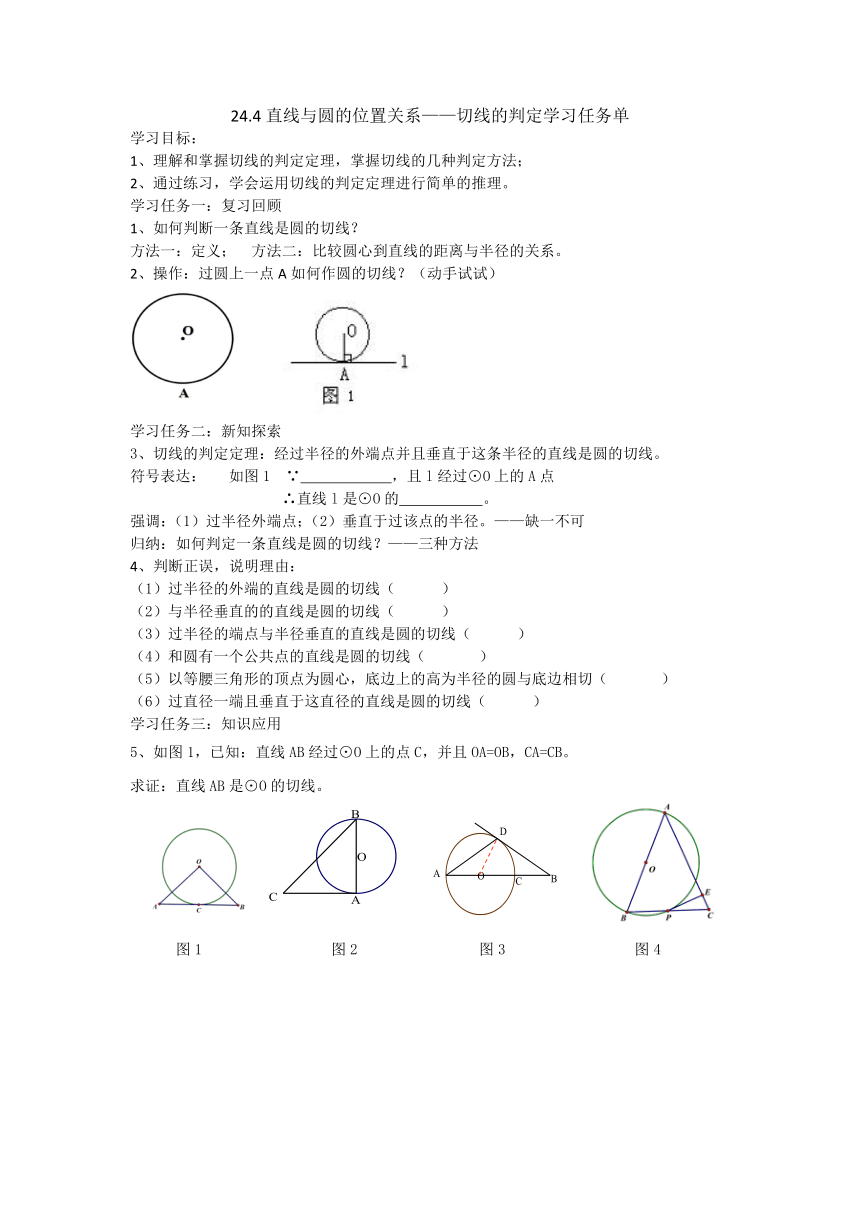
2、操作:过圆上一点A如何作圆的切线?(动手试试)
学习任务二:新知探索
3、切线的判定定理:经过半径的外端点并且垂直于这条半径的直线是圆的切线。
符号表达:
如图1
∵
,且l经过⊙O上的A点
∴直线l是⊙O的
。
强调:(1)过半径外端点;(2)垂直于过该点的半径。——缺一不可
归纳:如何判定一条直线是圆的切线?——三种方法
4、判断正误,说明理由:
(1)过半径的外端的直线是圆的切线(
)
(2)与半径垂直的的直线是圆的切线(
)
(3)过半径的端点与半径垂直的直线是圆的切线(
)
(4)和圆有一个公共点的直线是圆的切线(
)
(5)以等腰三角形的顶点为圆心,底边上的高为半径的圆与底边相切(
)
(6)过直径一端且垂直于这直径的直线是圆的切线(
)
学习任务三:知识应用
5、如图1,已知:直线AB经过⊙O上的点C,并且OA=OB,CA=CB。
求证:直线AB是⊙O的切线。
图1
图2
图3
图4
变式应用:
6、如图2,AB是⊙O的直径,∠ABC=45°,AC=AB,AC是⊙O的切线吗?为什么?
7、如图3:线段AB经过圆心O,交⊙O于点A、C,∠BAD=∠B
=
30°,边BD交圆于点D。BD是⊙O的切线吗?为什么?
8、如图4,△ABC中,以AB为直径的⊙O交边BC于P,BP=PC,
PE⊥AC于E。
求证:PE是⊙O的切线。
9、如图5,已知:O为∠BAC平分线上一点,OD⊥AB于D,以O为圆心,OD为半径作⊙O。求证:⊙O与AC相切。
图5
图7
图8
图9
变式应用:
练习4、已知如图6,△ABC为等腰三角形,O是底边BC的中点,⊙O与腰AB相切于点D。AC与⊙O相切吗?为什么?
学习任务四:自主练习
10、如图7,AB是⊙O的直径,
C为⊙O上一点,AD和过点C的切线互相垂直,垂足为D。
求证:AC平分∠DAB。
11、如图8:AC是⊙O的切线,∠B=600。求∠CAD=
。
12、如图9:以O为圆心的同心圆,大圆的弦AB是小圆的切线,C是切点,求证:C是AB的中点。
学习任务五:总结收获、巩固拓展
略
学习目标:
1、理解和掌握切线的判定定理,掌握切线的几种判定方法;
2、通过练习,学会运用切线的判定定理进行简单的推理。
学习任务一:复习回顾
1、如何判断一条直线是圆的切线?
方法一:定义;
方法二:比较圆心到直线的距离与半径的关系。
2、操作:过圆上一点A如何作圆的切线?(动手试试)
学习任务二:新知探索
3、切线的判定定理:经过半径的外端点并且垂直于这条半径的直线是圆的切线。
符号表达:
如图1
∵
,且l经过⊙O上的A点
∴直线l是⊙O的
。
强调:(1)过半径外端点;(2)垂直于过该点的半径。——缺一不可
归纳:如何判定一条直线是圆的切线?——三种方法
4、判断正误,说明理由:
(1)过半径的外端的直线是圆的切线(
)
(2)与半径垂直的的直线是圆的切线(
)
(3)过半径的端点与半径垂直的直线是圆的切线(
)
(4)和圆有一个公共点的直线是圆的切线(
)
(5)以等腰三角形的顶点为圆心,底边上的高为半径的圆与底边相切(
)
(6)过直径一端且垂直于这直径的直线是圆的切线(
)
学习任务三:知识应用
5、如图1,已知:直线AB经过⊙O上的点C,并且OA=OB,CA=CB。
求证:直线AB是⊙O的切线。
图1
图2
图3
图4
变式应用:
6、如图2,AB是⊙O的直径,∠ABC=45°,AC=AB,AC是⊙O的切线吗?为什么?
7、如图3:线段AB经过圆心O,交⊙O于点A、C,∠BAD=∠B
=
30°,边BD交圆于点D。BD是⊙O的切线吗?为什么?
8、如图4,△ABC中,以AB为直径的⊙O交边BC于P,BP=PC,
PE⊥AC于E。
求证:PE是⊙O的切线。
9、如图5,已知:O为∠BAC平分线上一点,OD⊥AB于D,以O为圆心,OD为半径作⊙O。求证:⊙O与AC相切。
图5
图7
图8
图9
变式应用:
练习4、已知如图6,△ABC为等腰三角形,O是底边BC的中点,⊙O与腰AB相切于点D。AC与⊙O相切吗?为什么?
学习任务四:自主练习
10、如图7,AB是⊙O的直径,
C为⊙O上一点,AD和过点C的切线互相垂直,垂足为D。
求证:AC平分∠DAB。
11、如图8:AC是⊙O的切线,∠B=600。求∠CAD=
。
12、如图9:以O为圆心的同心圆,大圆的弦AB是小圆的切线,C是切点,求证:C是AB的中点。
学习任务五:总结收获、巩固拓展
略
