沪科版(2012)初中数学九年级下册 24.8 综合与实践:射门线路与最佳射门角 教案
文档属性
| 名称 | 沪科版(2012)初中数学九年级下册 24.8 综合与实践:射门线路与最佳射门角 教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 81.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-20 00:00:00 | ||
图片预览

文档简介
课题:24.8
综合与实践 进球线路与最佳射门角
【学习目标】
经历最佳射门角的探索过程;理解在弦的同侧同弦所对的圆外角、圆周角和圆内角的大小关系.
【学习重点】
最佳射门角的探索和推导;根据不同的带球路线寻找最佳射门点.
【学习难点】
运用在弦的同侧,同弦所对的圆外角、圆周角与圆内角的大小关系解决简单的实际射门问题.
知识链接:最佳射门角的实质是同弦所对的圆外角α、圆周角β和圆内角θ的大小比较,结果为α<β<θ.
【教学准备】课件、学案
教学过程
1、情景导入:
请大家先欣赏一段足球比赛视频。
设计意图:用激烈的足球比赛视频点燃激情,引发学生思考本节课探索和学习的内容.
2、新知介绍
足球运动员在球场上常需带球跑到一定位置后再进行射门,这个位置叫做射门点,射门点与球门边框两端点的夹角叫做射门角,一般来说射门角越大射门进球的可能性就越大.
3、新授
(1)
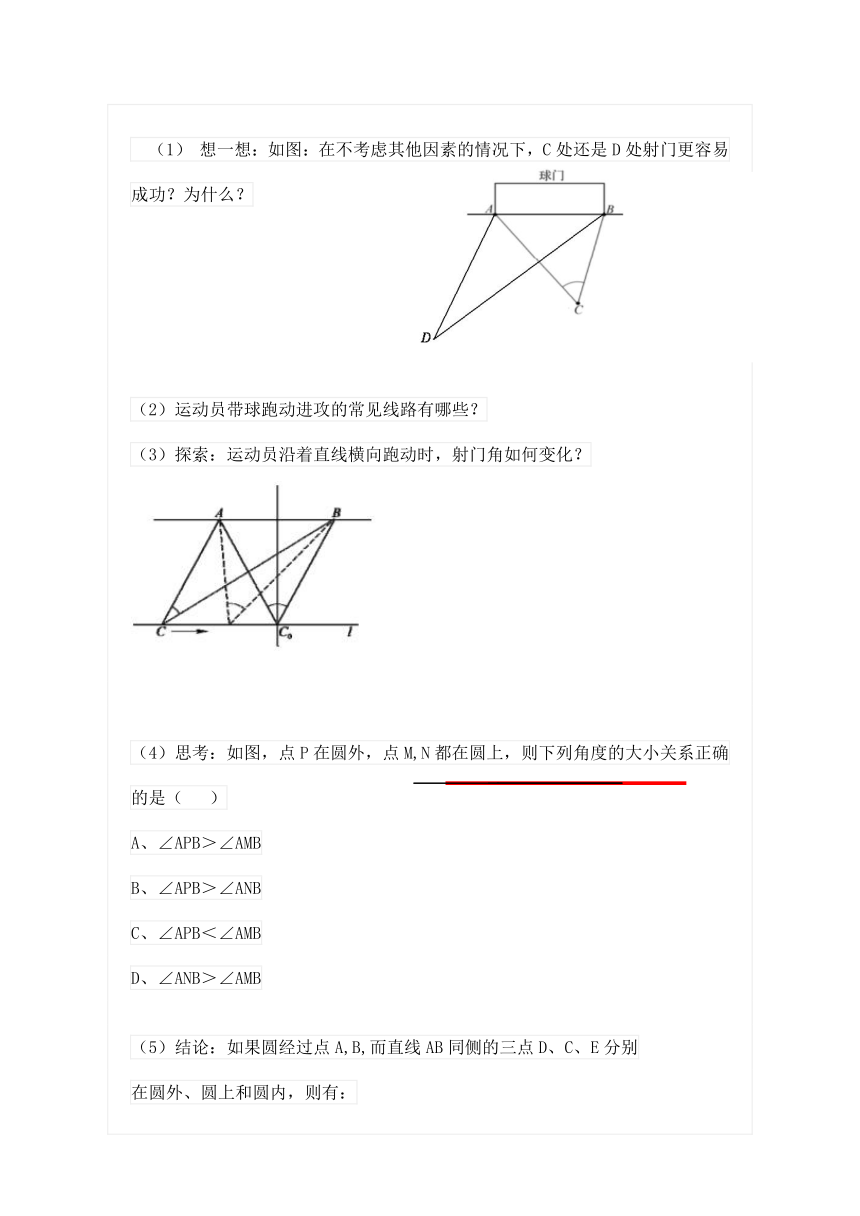
想一想:如图:在不考虑其他因素的情况下,C处还是D处射门更容易成功?为什么?
(2)运动员带球跑动进攻的常见线路有哪些?
(3)探索:运动员沿着直线横向跑动时,射门角如何变化?
(
A
B
M
P
N
)(4)思考:如图,点P在圆外,点M,N都在圆上,则下列角度的大小关系正确的是(
)
A、∠APB>∠AMB
B、∠APB>∠ANB
C、∠APB<∠AMB
D、∠ANB>∠AMB
(5)结论:如果圆经过点A,B,而直线AB同侧的三点D、C、E分别
在圆外、圆上和圆内,则有:
圆外角<圆周角<圆内角
请与同伴合作证明以上结论.
4、例题讲解
(
A
B
C
D
E
F
)例1:在足球比赛射门时,球对球门AB张开的角(射门角)越大,球越容易射进.在一场足球比赛中,如图队员甲已经把球带到对方球门前C处由于遇到防守队员死死盯防,他选择带球摆脱然后射门,有D、E、F三点供选择,则他选择哪个点射门效果最好?
5.继续新授
纵向跑动时的最佳射门点
(
A
B
D
C
)
当运动员的跑动路线垂直穿过球门AB时,∠ACB的大小如何变化?直线CD上还有最佳射门点吗?
6、当跑动路线与AB垂直但是垂足在线段AB外时,∠ACB的大小如何变化?最佳射门点在哪里?
结论:当直线与经过A、B的圆相切时,切点是最佳射门点.
7、学以致用
(
A
B
D
C
)如图,若AB=7,BD=3,当点C是垂直于AB的直线上的最佳射门点时,求CD的长.
8、课堂总结(颗粒归仓)
本节课你有哪些收获?
9.课后探索:当运动员斜向跑动时是否存在最佳射门点?如果存在,在哪里?
请你独立或与同学一起研究.
课后反思
1收获:____________________________________________________________________
2存在困惑:____________________________________________________________________
综合与实践 进球线路与最佳射门角
【学习目标】
经历最佳射门角的探索过程;理解在弦的同侧同弦所对的圆外角、圆周角和圆内角的大小关系.
【学习重点】
最佳射门角的探索和推导;根据不同的带球路线寻找最佳射门点.
【学习难点】
运用在弦的同侧,同弦所对的圆外角、圆周角与圆内角的大小关系解决简单的实际射门问题.
知识链接:最佳射门角的实质是同弦所对的圆外角α、圆周角β和圆内角θ的大小比较,结果为α<β<θ.
【教学准备】课件、学案
教学过程
1、情景导入:
请大家先欣赏一段足球比赛视频。
设计意图:用激烈的足球比赛视频点燃激情,引发学生思考本节课探索和学习的内容.
2、新知介绍
足球运动员在球场上常需带球跑到一定位置后再进行射门,这个位置叫做射门点,射门点与球门边框两端点的夹角叫做射门角,一般来说射门角越大射门进球的可能性就越大.
3、新授
(1)
想一想:如图:在不考虑其他因素的情况下,C处还是D处射门更容易成功?为什么?
(2)运动员带球跑动进攻的常见线路有哪些?
(3)探索:运动员沿着直线横向跑动时,射门角如何变化?
(
A
B
M
P
N
)(4)思考:如图,点P在圆外,点M,N都在圆上,则下列角度的大小关系正确的是(
)
A、∠APB>∠AMB
B、∠APB>∠ANB
C、∠APB<∠AMB
D、∠ANB>∠AMB
(5)结论:如果圆经过点A,B,而直线AB同侧的三点D、C、E分别
在圆外、圆上和圆内,则有:
圆外角<圆周角<圆内角
请与同伴合作证明以上结论.
4、例题讲解
(
A
B
C
D
E
F
)例1:在足球比赛射门时,球对球门AB张开的角(射门角)越大,球越容易射进.在一场足球比赛中,如图队员甲已经把球带到对方球门前C处由于遇到防守队员死死盯防,他选择带球摆脱然后射门,有D、E、F三点供选择,则他选择哪个点射门效果最好?
5.继续新授
纵向跑动时的最佳射门点
(
A
B
D
C
)
当运动员的跑动路线垂直穿过球门AB时,∠ACB的大小如何变化?直线CD上还有最佳射门点吗?
6、当跑动路线与AB垂直但是垂足在线段AB外时,∠ACB的大小如何变化?最佳射门点在哪里?
结论:当直线与经过A、B的圆相切时,切点是最佳射门点.
7、学以致用
(
A
B
D
C
)如图,若AB=7,BD=3,当点C是垂直于AB的直线上的最佳射门点时,求CD的长.
8、课堂总结(颗粒归仓)
本节课你有哪些收获?
9.课后探索:当运动员斜向跑动时是否存在最佳射门点?如果存在,在哪里?
请你独立或与同学一起研究.
课后反思
1收获:____________________________________________________________________
2存在困惑:____________________________________________________________________
