北师大版数学七年级下册5.1 轴对称现象 课件(23张)
文档属性
| 名称 | 北师大版数学七年级下册5.1 轴对称现象 课件(23张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-19 00:00:00 | ||
图片预览








文档简介
第五章 生活中的轴对称
1 轴对称现象
1.通过观察实例,了解轴对称图形和两个图形成轴对称的概念.(重点)
2.掌握轴对称图形的性质和成轴对称的两个图形的性质并能解决实际问题.(难点)
学习目标
新课导入
情境导入
仔细观察,你能从这些图片中得到什么规律?
归 纳
以上图形沿着一条直线翻折后,直线两旁的两个部分能够完全重合.
新课讲解
知识点1 轴对称图形
概念: 如果一个平面图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形,这条直线就是它的对称轴.
此时,也说这个图形关于这条直线(成轴)对称.
(1)轴对称图形是对一个图形来讲的,它是一个图形自身的对称特征,它被对称轴分成的两部分能够互相重合.
(2)一个轴对称图形的对称轴可以有一条,也可以有多条.
新课讲解
知识点1 全等形
根据以上的定义,你能举出生活中见过的一些轴对称图形的例子吗?
新课讲解
练一练
以下图形哪些是轴对称图形
1
是 是 不是
是 不是 是
新课讲解
练一练
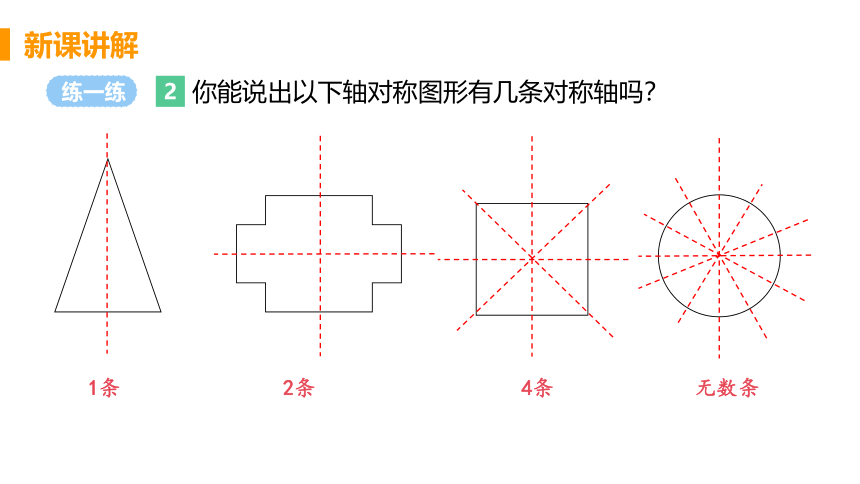
你能说出以下轴对称图形有几条对称轴吗?
2
1条 2条 4条 无数条
新课讲解
1、一个轴对称图形的对称轴可以有一条,也可以有多条,甚至有无数条.
2、轴对称图形的对称轴通常画成直线、虚线.
思考:以下常见的轴对称图形分别有几条对称轴,对称轴分别是哪些直线?
角、等腰三角形、等边三角形、等腰梯形、长方形、正方形、正五边形、正六边形、圆.
新课讲解
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}图形名称
图形
对称轴
对称轴的条数
角
角平分线所在的直线
1
等腰三角形
底边上的高(底边上的中线、顶角平分线)所在的直线
1
等边三角形
各边上的高(内角平分线、各边上的中线)所在的直线
3
等腰梯形
上、下底的中点所在的直线
1
长方形
对边中点所在的直线
2
新课讲解
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}图形名称
图形
对称轴
对称轴的条数
正方形
对边中点所在的直线
两条对角线所在的直线
4
正五边形
过一边中点且与该边垂直的直线
5
正六边形
相对的顶点所在的直线
对边中点所在的直线
6
圆
过圆心的每一条直线
无数
新课导入
情境导入
仔细观察,下列每对图片有什么共同特点?
图中的每一对图形沿着虚线折叠,左边的图形能够和右边的图形重合.
归 纳
新课讲解
知识点2 轴对称
概念:把一个图形沿着某一条直线折叠,如果它能够与另外一个图形重合,那么就说这两个图形关于这条直线(成轴)对称.这条直线叫做对称轴,折叠后能够重合的点是对应点,叫做对称点.
理解轴对称定义的三点:1、有两个图形;2、存在一条直线;3、使得一个图形沿着这条直线折叠后与另外一个图形重合.
新课讲解
练一练
分别观察以下每组图形,判断它们是否关于某条直线成轴对称?
1
是 不是 是
不是 不是 是
E
E
E
E
E
E
E
E
E
E
E
E
新课讲解
练一练
仔细观察,下列两个图形有什么区别?
2
轴对称图形
两个图形成轴对称
新课讲解
轴对称图形和轴对称的区别和联系
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A} 名 称
关 系
轴对称图形
轴对称
区别
对象不同
意义不同
对称点和位置不同
对称轴的数量不同
联系
一个图形
两个图形
一个形状特殊的图形
两个图形之间的特殊关系
对称点在这个图形上
对称点分别在这两个图形上
一条或者多条或者无数条
只有一条
1、都能沿着某条直线折叠后相互重合;
2、把成轴对称的两个图形看成一个整体,它就是一个轴对称图形.把一个轴对称图形沿着对称轴分成两个图形,这两个图形关于这条轴对称.
新课讲解
练一练
1
D
如下字体的四个汉字,是轴对称图形的是( )
A.书 B.香 C.宜 D.昌
选项D中的汉字沿着竖直的一条直线折叠,直线两旁的部分能够互相重合.注意B选项和C选项中均不能满足轴对称图形的定义,要看清楚香的“禾”和宜的 “宀”.
新课讲解
练一练
2
如图所示的每个图形是轴对称图形吗?如果是,指出它的对称轴.
是,1条
不是
是,2条
是,4条
新课讲解
练一练
如图所示的每幅图形中的两个图案是轴对称吗?如果是,指出它的对称轴和对称点.
3
C1
A1
B1
D1
E1
是
A和A1,B和B1,C和C1,D和D1,E和E1.
A1
B1
C1
D1
是
A和A1,B和B1,
C和C1,D和D1.
G
G
不是
课堂小结
轴对称图形
轴对称图形和两个图形成轴对称
区别和联系
应用
利用轴对称图形和两个图形成轴对称的定义进行判断
定义
1、轴对称图形
2、两个图形成轴对称
当堂小练
下列图形,不是轴对称图形的是( )
C
A
B
C
D
当堂小练
判断下列说法的对错:
1、轴对称图形必有对称轴.( )
2、轴对称图形至少有一条对称轴.( )
3、关于某直线成轴对称的两个图形必能互相重合.( )
4、两个完全互相重合的图形必是轴对称.( )
5、两个图形成轴对称,则这两个图形是全等形.( )
√
√
√
×
√
D
拓展与延伸
完成下列填空:
1、成轴对称的两个图形的对应角( ),对应边( ).
2、在“线段、钝角、长方形、等边三角形”这四个图形中,是轴对称图形的有( )个,其中对称轴最多的是( ),线段的对称轴是( ).
3、成轴对称的两个图形( )全等形;把一个轴对称图形沿着对称轴分成两个图形,这两个图形( )全等形.(填“是”或“否”)
相等
相等
4
等边三角形
经过线段中点且垂直于线段的直线
是
是
布置作业
请完成对应习题
1 轴对称现象
1.通过观察实例,了解轴对称图形和两个图形成轴对称的概念.(重点)
2.掌握轴对称图形的性质和成轴对称的两个图形的性质并能解决实际问题.(难点)
学习目标
新课导入
情境导入
仔细观察,你能从这些图片中得到什么规律?
归 纳
以上图形沿着一条直线翻折后,直线两旁的两个部分能够完全重合.
新课讲解
知识点1 轴对称图形
概念: 如果一个平面图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形,这条直线就是它的对称轴.
此时,也说这个图形关于这条直线(成轴)对称.
(1)轴对称图形是对一个图形来讲的,它是一个图形自身的对称特征,它被对称轴分成的两部分能够互相重合.
(2)一个轴对称图形的对称轴可以有一条,也可以有多条.
新课讲解
知识点1 全等形
根据以上的定义,你能举出生活中见过的一些轴对称图形的例子吗?
新课讲解
练一练
以下图形哪些是轴对称图形
1
是 是 不是
是 不是 是
新课讲解
练一练
你能说出以下轴对称图形有几条对称轴吗?
2
1条 2条 4条 无数条
新课讲解
1、一个轴对称图形的对称轴可以有一条,也可以有多条,甚至有无数条.
2、轴对称图形的对称轴通常画成直线、虚线.
思考:以下常见的轴对称图形分别有几条对称轴,对称轴分别是哪些直线?
角、等腰三角形、等边三角形、等腰梯形、长方形、正方形、正五边形、正六边形、圆.
新课讲解
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}图形名称
图形
对称轴
对称轴的条数
角
角平分线所在的直线
1
等腰三角形
底边上的高(底边上的中线、顶角平分线)所在的直线
1
等边三角形
各边上的高(内角平分线、各边上的中线)所在的直线
3
等腰梯形
上、下底的中点所在的直线
1
长方形
对边中点所在的直线
2
新课讲解
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}图形名称
图形
对称轴
对称轴的条数
正方形
对边中点所在的直线
两条对角线所在的直线
4
正五边形
过一边中点且与该边垂直的直线
5
正六边形
相对的顶点所在的直线
对边中点所在的直线
6
圆
过圆心的每一条直线
无数
新课导入
情境导入
仔细观察,下列每对图片有什么共同特点?
图中的每一对图形沿着虚线折叠,左边的图形能够和右边的图形重合.
归 纳
新课讲解
知识点2 轴对称
概念:把一个图形沿着某一条直线折叠,如果它能够与另外一个图形重合,那么就说这两个图形关于这条直线(成轴)对称.这条直线叫做对称轴,折叠后能够重合的点是对应点,叫做对称点.
理解轴对称定义的三点:1、有两个图形;2、存在一条直线;3、使得一个图形沿着这条直线折叠后与另外一个图形重合.
新课讲解
练一练
分别观察以下每组图形,判断它们是否关于某条直线成轴对称?
1
是 不是 是
不是 不是 是
E
E
E
E
E
E
E
E
E
E
E
E
新课讲解
练一练
仔细观察,下列两个图形有什么区别?
2
轴对称图形
两个图形成轴对称
新课讲解
轴对称图形和轴对称的区别和联系
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A} 名 称
关 系
轴对称图形
轴对称
区别
对象不同
意义不同
对称点和位置不同
对称轴的数量不同
联系
一个图形
两个图形
一个形状特殊的图形
两个图形之间的特殊关系
对称点在这个图形上
对称点分别在这两个图形上
一条或者多条或者无数条
只有一条
1、都能沿着某条直线折叠后相互重合;
2、把成轴对称的两个图形看成一个整体,它就是一个轴对称图形.把一个轴对称图形沿着对称轴分成两个图形,这两个图形关于这条轴对称.
新课讲解
练一练
1
D
如下字体的四个汉字,是轴对称图形的是( )
A.书 B.香 C.宜 D.昌
选项D中的汉字沿着竖直的一条直线折叠,直线两旁的部分能够互相重合.注意B选项和C选项中均不能满足轴对称图形的定义,要看清楚香的“禾”和宜的 “宀”.
新课讲解
练一练
2
如图所示的每个图形是轴对称图形吗?如果是,指出它的对称轴.
是,1条
不是
是,2条
是,4条
新课讲解
练一练
如图所示的每幅图形中的两个图案是轴对称吗?如果是,指出它的对称轴和对称点.
3
C1
A1
B1
D1
E1
是
A和A1,B和B1,C和C1,D和D1,E和E1.
A1
B1
C1
D1
是
A和A1,B和B1,
C和C1,D和D1.
G
G
不是
课堂小结
轴对称图形
轴对称图形和两个图形成轴对称
区别和联系
应用
利用轴对称图形和两个图形成轴对称的定义进行判断
定义
1、轴对称图形
2、两个图形成轴对称
当堂小练
下列图形,不是轴对称图形的是( )
C
A
B
C
D
当堂小练
判断下列说法的对错:
1、轴对称图形必有对称轴.( )
2、轴对称图形至少有一条对称轴.( )
3、关于某直线成轴对称的两个图形必能互相重合.( )
4、两个完全互相重合的图形必是轴对称.( )
5、两个图形成轴对称,则这两个图形是全等形.( )
√
√
√
×
√
D
拓展与延伸
完成下列填空:
1、成轴对称的两个图形的对应角( ),对应边( ).
2、在“线段、钝角、长方形、等边三角形”这四个图形中,是轴对称图形的有( )个,其中对称轴最多的是( ),线段的对称轴是( ).
3、成轴对称的两个图形( )全等形;把一个轴对称图形沿着对称轴分成两个图形,这两个图形( )全等形.(填“是”或“否”)
相等
相等
4
等边三角形
经过线段中点且垂直于线段的直线
是
是
布置作业
请完成对应习题
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
