北师大版数学七年级下册5.3.2 线段的垂直平分线 课件(22张)
文档属性
| 名称 | 北师大版数学七年级下册5.3.2 线段的垂直平分线 课件(22张) |  | |
| 格式 | pptx | ||
| 文件大小 | 749.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-19 23:41:52 | ||
图片预览








文档简介
第五章 生活中的轴对称
3 简单的轴对称图形
课时2 线段的垂直平分线
1.理解并掌握线段垂直平分线的定义.(重点)
2.熟悉轴对称图形和轴对称图形的性质.(难点)
3.综合运用轴对称图形的性质、线段垂直平分线来解决实际问题.
学习目标
新课导入
思 考
如图,△ABC和△A'B'C'关于直线MN对称,点A',B',C'分别是点A,B,C的对称点,线段AA',BB',CC'与直线MN有什么关系?
解:∵△ABC和△A'B'C'关于直线MN对称,
∴将△ABC沿着MN折叠后能和△A'B'C'完全重合.
∴点A和点A',点B和点B',点C和点C'是对称点.
C'
B
B'
A'
M
N
A
C
新课导入
C'
B
B'
A'
M
N
A
C
设AA',BB',CC'分别交直线MN于点P,E,F,
则有AP=A'P,∠MPA=∠MPA'=90°;
BE=B'E,∠MEB=∠MEB'=90°;
CF=C'F',∠MFC=∠MFC'=90°.
因此,对称轴经过对称点所连线段的中点,并且
垂直于这条线段.
新课讲解
知识点1 线段的垂直平分线
概念: 经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线.
几何语言:如图所示,直线l是线段AB的垂直平分线.
则:AO=BO,l⊥AB.
A
B
l
O
┐
1、线段的垂直平分线必须满足两个条件:①经过这条线段的中点;②垂直于这条线段.这二者缺一不可.
2、线段的垂直平分线是一条直线.
3、线段垂直平分线也可以称为“中垂线”.
新课讲解
知识点2 图形轴对称的性质
如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.
如图,五边形ABCDE是轴对称图形,直线MN是对称轴,则直线 MN是线段AD,BC的垂直平分线.
A
B
D
C
M
N
E
新课讲解
知识点2 图形轴对称的性质:
新课讲解
练一练
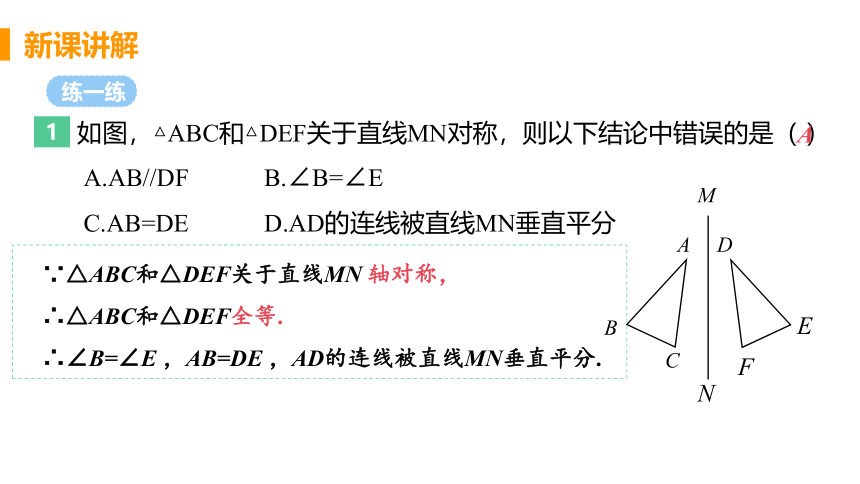
如图,△ABC和△DEF关于直线MN对称,则以下结论中错误的是( )
A.AB//DF B.∠B=∠E
C.AB=DE D.AD的连线被直线MN垂直平分
1
A
B
C
D
E
F
M
N
∵△ABC和△DEF关于直线MN 轴对称,
∴△ABC和△DEF全等.
∴∠B=∠E ,AB=DE ,AD的连线被直线MN垂直平分.
A
新课讲解
练一练
如图,直线MN是四边形AMBN的对称轴,点P是直线MN上的点,下列判断错误的是( )
A.AM=BM B.AP=BN
C.∠MAP=∠MBP D.∠ANM=∠BNM
3
∵直线MN是四边形AMBN的对称轴,且点A和点B是对称点,
∴AM=BM,AN=BN,∠ANM=∠BNM.
∵点P是直线MN上的点,
∴∠PAN=∠PBN,∠MAN=∠MBN.
∴∠MAN-∠PAN=∠MBN-∠PBN,即∠MAP=∠MBP.
B
A
N
M
B
课堂小结
线段垂直平分线
轴对称图形的对称轴,是任何一对对应点所连线段的垂直平分线
轴对称图形的性质
图形轴对称的性质
如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线
定义
经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线
当堂小练
如图,在3×3的正方形网格中,有两个小正方形已被涂上阴影,再将图中剩余小正方形中任意一个涂上阴影,那么能使整个图案构成一个轴对称图形的涂法有( )
A.5种 B.6种 C.4种 D.7种
分析:图中是3×3的正方形网格,已经涂上2个阴影,还剩下7个,选择合适的对称轴,根据轴对称图形的概念找出正确的图法,保证不重不漏.
当堂小练
如图,在3×3的正方形网格中,有两个小正方形已被涂上阴影,再将图中剩余小正方形中任意一个涂上阴影,那么能使整个图案构成一个轴对称图形的涂法有( )
A.5种 B.6种 C.4种 D.7种
A
当堂小练
如果三角形三条边的垂直平分线的交点在三角形的外部,那么这个三角形是( )
A.直角三角形 B.锐角三角形
C.钝角三角形 D. 等边三角形
C
拓展与延伸
如图,在正方形中均匀分布着一些数字,小明利用轴对称的思想,用了一种非常简便的方法,迅速地将这些数字的和求了出来,你知道他是怎么求出来的吗?
从正方形中数字的排列可以看出,其中一条对角线上的数字都是5,若把对角线所在的直线当作对称轴,把正方形翻折一下,则除对称轴以外的其他对称位置的两数之和都是10.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}1
2
3
4
5
2
3
4
5
6
3
4
5
6
7
4
5
6
7
8
5
6
7
8
9
拓展与延伸
如图,在正方形中均匀分布着一些数字,小明利用轴对称的思想,用了一种非常简便的方法,迅速地将这些数字的和求了出来,你知道他是怎么求出来的吗?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}1
2
3
4
5
2
3
4
5
6
3
4
5
6
7
4
5
6
7
8
5
6
7
8
9
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
5
5
10
5
10
10
5
10
10
10
5
10
10
10
10
正方形的数字之和10×10+5×5=125
拓展与延伸
(1)在△ABC中,AB=AC,AB的垂直平分线交AB于N,交BC的延长线于 M,∠A=50°,求∠NMB的大小.
(2)如果将(1)中∠A的度数改为80°,其余条件不变,再求∠NMB的大小.
(3)你发现有什么规律?请尝试证明.
(4)将(1)中的∠A改为钝角,对这个问题发现的规律是否需要加以修改?
A
B
C
A
B
C
A
B
C
N
M
N
M
N
M
拓展与延伸
(1)在△ABC中,AB=AC,AB的垂直平分线交AB于N,交BC的延长线于 M,∠A=50°,求∠NMB的大小.
(2)如果将(1)中∠A的度数改为80°,其余条件不变,再求∠NMB的大小.
(3)你发现有什么规律?请尝试证明.
(4)将(1)中的∠A改为钝角,对这个问题发现的规律是否需要加以修改?
A
B
C
A
B
C
A
B
C
N
M
N
M
N
M
拓展与延伸
(1)在△ABC中,AB=AC,AB的垂直平分线交AB于N,交BC的延长线于 M,∠A=50°,求∠NMB的大小.
(2)如果将(1)中∠A的度数改为80°,其余条件不变,再求∠NMB的大小.
(3)你发现有什么规律?请尝试证明.
(4)将(1)中的∠A改为钝角,对这个问题发现的规律是否需要加以修改?
A
B
C
A
B
C
A
B
C
N
M
N
M
N
M
拓展与延伸
(1)在△ABC中,AB=AC,AB的垂直平分线交AB于N,交BC的延长线于 M,∠A=50°,求∠NMB的大小.
(2)如果将(1)中∠A的度数改为80°,其余条件不变,再求∠NMB的大小.
(3)你发现有什么规律?请尝试证明.
(4)将(1)中的∠A改为钝角,对这个问题发现的规律是否需要加以修改?
A
B
C
A
B
C
A
B
C
N
M
N
M
N
M
拓展与延伸
(1)解:∵AB的垂直平分线交AB于N, ∴∠MNB=∠MNA=90°.
∵∠B= (180°-∠A)=65°, ∴∠NMB=90°-∠B=25°.
(2)解:∵AB的垂直平分线交AB于N, ∴∠MNB=∠MNA=90°.
∵∠B= (180°-∠A)=50°, ∴∠NMB=90°-∠B=40°.
(3)证明:设∠A=a,
∵AB的垂直平分线交AB于N, ∴∠MNB=∠MNA=90°.
∵∠B= (180°-a) , ∴∠NMB=90°-∠B=a.
拓展与延伸
(4)改为钝角后规律仍然成立,上述规律为:等腰三角形一腰的垂直平分线与底边相交所构成的锐角等于顶角的一半.
布置作业
请完成对应习题
3 简单的轴对称图形
课时2 线段的垂直平分线
1.理解并掌握线段垂直平分线的定义.(重点)
2.熟悉轴对称图形和轴对称图形的性质.(难点)
3.综合运用轴对称图形的性质、线段垂直平分线来解决实际问题.
学习目标
新课导入
思 考
如图,△ABC和△A'B'C'关于直线MN对称,点A',B',C'分别是点A,B,C的对称点,线段AA',BB',CC'与直线MN有什么关系?
解:∵△ABC和△A'B'C'关于直线MN对称,
∴将△ABC沿着MN折叠后能和△A'B'C'完全重合.
∴点A和点A',点B和点B',点C和点C'是对称点.
C'
B
B'
A'
M
N
A
C
新课导入
C'
B
B'
A'
M
N
A
C
设AA',BB',CC'分别交直线MN于点P,E,F,
则有AP=A'P,∠MPA=∠MPA'=90°;
BE=B'E,∠MEB=∠MEB'=90°;
CF=C'F',∠MFC=∠MFC'=90°.
因此,对称轴经过对称点所连线段的中点,并且
垂直于这条线段.
新课讲解
知识点1 线段的垂直平分线
概念: 经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线.
几何语言:如图所示,直线l是线段AB的垂直平分线.
则:AO=BO,l⊥AB.
A
B
l
O
┐
1、线段的垂直平分线必须满足两个条件:①经过这条线段的中点;②垂直于这条线段.这二者缺一不可.
2、线段的垂直平分线是一条直线.
3、线段垂直平分线也可以称为“中垂线”.
新课讲解
知识点2 图形轴对称的性质
如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.
如图,五边形ABCDE是轴对称图形,直线MN是对称轴,则直线 MN是线段AD,BC的垂直平分线.
A
B
D
C
M
N
E
新课讲解
知识点2 图形轴对称的性质:
新课讲解
练一练
如图,△ABC和△DEF关于直线MN对称,则以下结论中错误的是( )
A.AB//DF B.∠B=∠E
C.AB=DE D.AD的连线被直线MN垂直平分
1
A
B
C
D
E
F
M
N
∵△ABC和△DEF关于直线MN 轴对称,
∴△ABC和△DEF全等.
∴∠B=∠E ,AB=DE ,AD的连线被直线MN垂直平分.
A
新课讲解
练一练
如图,直线MN是四边形AMBN的对称轴,点P是直线MN上的点,下列判断错误的是( )
A.AM=BM B.AP=BN
C.∠MAP=∠MBP D.∠ANM=∠BNM
3
∵直线MN是四边形AMBN的对称轴,且点A和点B是对称点,
∴AM=BM,AN=BN,∠ANM=∠BNM.
∵点P是直线MN上的点,
∴∠PAN=∠PBN,∠MAN=∠MBN.
∴∠MAN-∠PAN=∠MBN-∠PBN,即∠MAP=∠MBP.
B
A
N
M
B
课堂小结
线段垂直平分线
轴对称图形的对称轴,是任何一对对应点所连线段的垂直平分线
轴对称图形的性质
图形轴对称的性质
如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线
定义
经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线
当堂小练
如图,在3×3的正方形网格中,有两个小正方形已被涂上阴影,再将图中剩余小正方形中任意一个涂上阴影,那么能使整个图案构成一个轴对称图形的涂法有( )
A.5种 B.6种 C.4种 D.7种
分析:图中是3×3的正方形网格,已经涂上2个阴影,还剩下7个,选择合适的对称轴,根据轴对称图形的概念找出正确的图法,保证不重不漏.
当堂小练
如图,在3×3的正方形网格中,有两个小正方形已被涂上阴影,再将图中剩余小正方形中任意一个涂上阴影,那么能使整个图案构成一个轴对称图形的涂法有( )
A.5种 B.6种 C.4种 D.7种
A
当堂小练
如果三角形三条边的垂直平分线的交点在三角形的外部,那么这个三角形是( )
A.直角三角形 B.锐角三角形
C.钝角三角形 D. 等边三角形
C
拓展与延伸
如图,在正方形中均匀分布着一些数字,小明利用轴对称的思想,用了一种非常简便的方法,迅速地将这些数字的和求了出来,你知道他是怎么求出来的吗?
从正方形中数字的排列可以看出,其中一条对角线上的数字都是5,若把对角线所在的直线当作对称轴,把正方形翻折一下,则除对称轴以外的其他对称位置的两数之和都是10.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}1
2
3
4
5
2
3
4
5
6
3
4
5
6
7
4
5
6
7
8
5
6
7
8
9
拓展与延伸
如图,在正方形中均匀分布着一些数字,小明利用轴对称的思想,用了一种非常简便的方法,迅速地将这些数字的和求了出来,你知道他是怎么求出来的吗?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}1
2
3
4
5
2
3
4
5
6
3
4
5
6
7
4
5
6
7
8
5
6
7
8
9
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
5
5
10
5
10
10
5
10
10
10
5
10
10
10
10
正方形的数字之和10×10+5×5=125
拓展与延伸
(1)在△ABC中,AB=AC,AB的垂直平分线交AB于N,交BC的延长线于 M,∠A=50°,求∠NMB的大小.
(2)如果将(1)中∠A的度数改为80°,其余条件不变,再求∠NMB的大小.
(3)你发现有什么规律?请尝试证明.
(4)将(1)中的∠A改为钝角,对这个问题发现的规律是否需要加以修改?
A
B
C
A
B
C
A
B
C
N
M
N
M
N
M
拓展与延伸
(1)在△ABC中,AB=AC,AB的垂直平分线交AB于N,交BC的延长线于 M,∠A=50°,求∠NMB的大小.
(2)如果将(1)中∠A的度数改为80°,其余条件不变,再求∠NMB的大小.
(3)你发现有什么规律?请尝试证明.
(4)将(1)中的∠A改为钝角,对这个问题发现的规律是否需要加以修改?
A
B
C
A
B
C
A
B
C
N
M
N
M
N
M
拓展与延伸
(1)在△ABC中,AB=AC,AB的垂直平分线交AB于N,交BC的延长线于 M,∠A=50°,求∠NMB的大小.
(2)如果将(1)中∠A的度数改为80°,其余条件不变,再求∠NMB的大小.
(3)你发现有什么规律?请尝试证明.
(4)将(1)中的∠A改为钝角,对这个问题发现的规律是否需要加以修改?
A
B
C
A
B
C
A
B
C
N
M
N
M
N
M
拓展与延伸
(1)在△ABC中,AB=AC,AB的垂直平分线交AB于N,交BC的延长线于 M,∠A=50°,求∠NMB的大小.
(2)如果将(1)中∠A的度数改为80°,其余条件不变,再求∠NMB的大小.
(3)你发现有什么规律?请尝试证明.
(4)将(1)中的∠A改为钝角,对这个问题发现的规律是否需要加以修改?
A
B
C
A
B
C
A
B
C
N
M
N
M
N
M
拓展与延伸
(1)解:∵AB的垂直平分线交AB于N, ∴∠MNB=∠MNA=90°.
∵∠B= (180°-∠A)=65°, ∴∠NMB=90°-∠B=25°.
(2)解:∵AB的垂直平分线交AB于N, ∴∠MNB=∠MNA=90°.
∵∠B= (180°-∠A)=50°, ∴∠NMB=90°-∠B=40°.
(3)证明:设∠A=a,
∵AB的垂直平分线交AB于N, ∴∠MNB=∠MNA=90°.
∵∠B= (180°-a) , ∴∠NMB=90°-∠B=a.
拓展与延伸
(4)改为钝角后规律仍然成立,上述规律为:等腰三角形一腰的垂直平分线与底边相交所构成的锐角等于顶角的一半.
布置作业
请完成对应习题
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
