甘肃省油田第一中学2020-2021学年高一上学期期末考试数学试题 Word版含答案
文档属性
| 名称 | 甘肃省油田第一中学2020-2021学年高一上学期期末考试数学试题 Word版含答案 |
|
|
| 格式 | doc | ||
| 文件大小 | 629.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-20 00:00:00 | ||
图片预览



文档简介
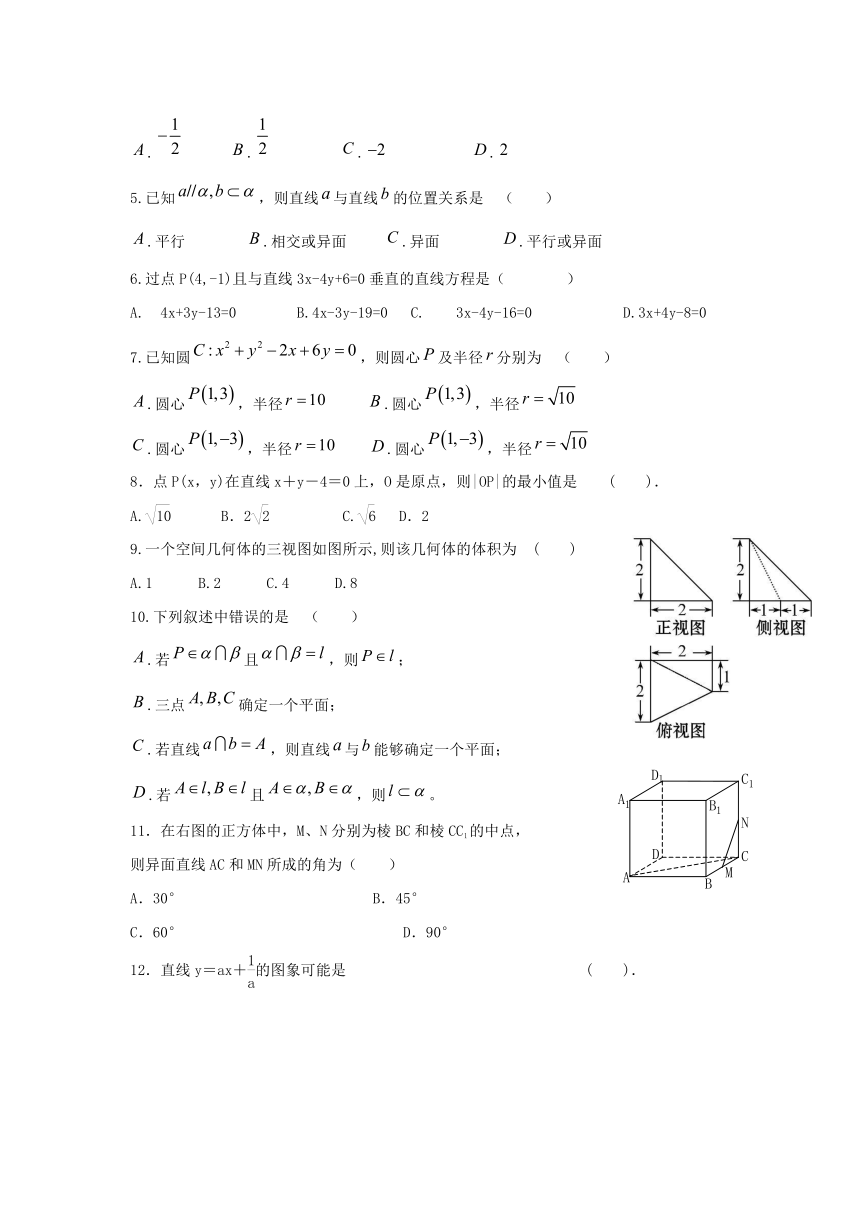
玉门油田第一中学2020-2021学年第一学期期末考试
高一数学试卷
命题:
一、选择题(本大题共12道小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的)
1.直线的方程为x-y+2018=0,则直线的倾斜角为 ( )
A.30° B.60° C.120° D.150°
2. 如图⑴、⑵、⑶、⑷为四个几何体的三视图,根据三视图可以判断这四个几何体依次分别为( )
A.三棱台、三棱柱、圆锥、圆台 B.三棱台、三棱锥、圆锥、圆台
C.三棱柱、正四棱锥、圆锥、圆台 D三棱柱、三棱台、圆锥、圆台
3.边长为正四面体的表面积是 ( )
. . . .
4.已知两条直线,且,则满足条件的值为 ( )
. . . .
5.已知,则直线与直线的位置关系是 ( )
.平行 .相交或异面 .异面 .平行或异面
6.过点P(4,-1)且与直线3x-4y+6=0垂直的直线方程是(????)
A.?4x+3y-13=0????B.4x-3y-19=0 C.??3x-4y-16=0??????D.3x+4y-8=0
7.已知圆,则圆心及半径分别为 ( )
.圆心,半径 .圆心,半径
.圆心,半径 .圆心,半径
8.点P(x,y)在直线x+y-4=0上,O是原点,则|OP|的最小值是 ( ).
A. B.2 C. D.2
9.一个空间几何体的三视图如图所示,则该几何体的体积为 ( )
A.1 B.2 C.4 D.8
10.下列叙述中错误的是 ( )
.若且,则;
.三点确定一个平面;
.若直线,则直线与能够确定一个平面;
.若且,则。
11.在右图的正方体中,M、N分别为棱BC和棱CC1的中点,
则异面直线AC和MN所成的角为( )
A.30° B.45°
C.60° D.90°
12.直线y=ax+的图象可能是 ( ).
二、填空题(本大题共4道小题,每小题5分,共20分。把答案填在题中横线上)
13.过点(1,2),且在两坐标轴上截距相等的直线方程__________
14.已知点A(2,1),B(-2,3),C(0,1),在△ABC中,BC边上的中线长为________.
15.图(1)为长方体积木块堆成的几何体的三视图,此几何体共由________块木块堆成;
图(2)中的三视图表示的实物为_____________。
16.给出以下四个命题:
①如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行,
②如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直于这个平面
③如果一个平面内的无数条直线都平行于另一个平面,那么这两个平面互相平行
(4)如果一个平面经过另一个平面的一条垂线,则这两个平面垂直
其中正确的命题_______________
玉门油田第一中学2020-2021学年第一学期期末考试
高一数学答题卷
考号_____________班级__________姓名____________总分______________
一、选择题(本大题共12道小题,每小题5分,共60分)
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案
二、填空题(本大题共4道小题,每小题5分,共20分)
13.________________14___________________15_________________16___________________
三、解答题(本大题共6道小题,共74分。解答应写出文字说明、证明过程或演算步骤)
17.(本题10分)如图,在圆锥PO中,已知PO=,☉O的直径AB=2,C是的中点,D为AC的中点.求证:平面POD⊥平面PAC.
18.(本题12分)已知直线经过点,且斜率为.
(Ⅰ)求直线的方程;(Ⅱ)求与直线切于点(2,2),圆心在直线上的圆的方程.
19.(本题12分)如图所示,在空间四边形ABCD中,E,F分别为AB,AD的中点,G,H分别在BC,CD上,且BG∶GC=DH∶HC=1∶2,求证: (1)E,F,G,H四点共面.
(2)EG与HF的交点在直线AC上.
20.(本题12分)求经过直线L1:3x + 4y – 5 = 0与直线L2:2x – 3y + 8 = 0的交点M,且满足下列条件的直线方程
(1)与直线2x + y + 5 = 0平行 ; (2)与直线2x + y + 5 = 0垂直;
21.(本题12分)如图所示,在直三棱柱中,,,、分别为、的中点.
(Ⅰ)求证:; (Ⅱ)求证:.
22.(本题12分)已知圆的方程为:.
(1)试求的值,使圆的面积最小;
(2)求与满足(1)中条件的圆相切,且过点的直线方程.
答案
高一数学 命题人:
一.选择题(本大题共12道小题,每小题5分,共60分)
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 A C D C D A D B B B C B
二.填空题(本大题共4道小题,每小题5分,共20分)
14.
15.4 圆锥 16.①②④
三.解答题
17.PO⊥☉O,CA?平面☉O,
所以OP⊥AC.
因为AD=CD,所以OD⊥AC.
因为OP∩OD=O,
所以AC⊥平面POD.
因为AC?平面PAC,
所以平面POD⊥平面PAC...........(10)
18.(Ⅰ)由直线方程的点斜式,得
整理,得所求直线方程为 ……………4分
(Ⅱ)过点(2,2)与垂直的直线方程为, ……………6分
由得圆心为(5,6), ……………8分
∴半径, ……………10分
故所求圆的方程为. ………12分
19.(1)因为BG∶GC=DH∶HC=1∶2,
所以GH∥BD,
因为E,F分别为AB,AD的中点,
所以EF∥BD,所以EF∥GH,
所以E,F,G,H四点共面......................6分
(2)因为G,H不是BC,CD的中点,
所以EF∥GH,且EF≠GH,
所以EG与FH必相交,设交点为M,
因为EG?平面ABC,HG?平面ACD,
所以M∈平面ABC,且M∈平面ACD,
因为平面ABC∩平面ACD=AC,
所以M∈AC,
所以EG与HF的交点在直线AC上......................12分
20.解:解得--------4分
所以交点(-1,2)
(1)-----6分
直线方程为--------8分
(2)---------10分
直线方程为--------12分
21.解析:(Ⅰ)在直三棱柱中,
侧面⊥底面,且侧面∩底面=,
∵∠=90°,即,
∴平面
∵平面,∴. ……4分
∵,,∴是正方形,
∴,∴. …………… 6分
(Ⅱ)取的中点,连、. ………………8分
在△中,、是中点,
∴,,又∵,,∴,,………6分
故四边形是平行四边形,∴,…………10分
而 面,平面,∴面 ……12分
22.配方得圆的方程:
(1)当时,圆的半径有最小值1,此时圆的面积最小。
(2)当时,圆的方程为
设所求的直线方程为
即
由直线与圆相切,得,
所以切线方程为,即
又过点且与轴垂直的直线与圆也相切
所发所求的切线方程为与。
高一数学试卷
命题:
一、选择题(本大题共12道小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的)
1.直线的方程为x-y+2018=0,则直线的倾斜角为 ( )
A.30° B.60° C.120° D.150°
2. 如图⑴、⑵、⑶、⑷为四个几何体的三视图,根据三视图可以判断这四个几何体依次分别为( )
A.三棱台、三棱柱、圆锥、圆台 B.三棱台、三棱锥、圆锥、圆台
C.三棱柱、正四棱锥、圆锥、圆台 D三棱柱、三棱台、圆锥、圆台
3.边长为正四面体的表面积是 ( )
. . . .
4.已知两条直线,且,则满足条件的值为 ( )
. . . .
5.已知,则直线与直线的位置关系是 ( )
.平行 .相交或异面 .异面 .平行或异面
6.过点P(4,-1)且与直线3x-4y+6=0垂直的直线方程是(????)
A.?4x+3y-13=0????B.4x-3y-19=0 C.??3x-4y-16=0??????D.3x+4y-8=0
7.已知圆,则圆心及半径分别为 ( )
.圆心,半径 .圆心,半径
.圆心,半径 .圆心,半径
8.点P(x,y)在直线x+y-4=0上,O是原点,则|OP|的最小值是 ( ).
A. B.2 C. D.2
9.一个空间几何体的三视图如图所示,则该几何体的体积为 ( )
A.1 B.2 C.4 D.8
10.下列叙述中错误的是 ( )
.若且,则;
.三点确定一个平面;
.若直线,则直线与能够确定一个平面;
.若且,则。
11.在右图的正方体中,M、N分别为棱BC和棱CC1的中点,
则异面直线AC和MN所成的角为( )
A.30° B.45°
C.60° D.90°
12.直线y=ax+的图象可能是 ( ).
二、填空题(本大题共4道小题,每小题5分,共20分。把答案填在题中横线上)
13.过点(1,2),且在两坐标轴上截距相等的直线方程__________
14.已知点A(2,1),B(-2,3),C(0,1),在△ABC中,BC边上的中线长为________.
15.图(1)为长方体积木块堆成的几何体的三视图,此几何体共由________块木块堆成;
图(2)中的三视图表示的实物为_____________。
16.给出以下四个命题:
①如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行,
②如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直于这个平面
③如果一个平面内的无数条直线都平行于另一个平面,那么这两个平面互相平行
(4)如果一个平面经过另一个平面的一条垂线,则这两个平面垂直
其中正确的命题_______________
玉门油田第一中学2020-2021学年第一学期期末考试
高一数学答题卷
考号_____________班级__________姓名____________总分______________
一、选择题(本大题共12道小题,每小题5分,共60分)
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案
二、填空题(本大题共4道小题,每小题5分,共20分)
13.________________14___________________15_________________16___________________
三、解答题(本大题共6道小题,共74分。解答应写出文字说明、证明过程或演算步骤)
17.(本题10分)如图,在圆锥PO中,已知PO=,☉O的直径AB=2,C是的中点,D为AC的中点.求证:平面POD⊥平面PAC.
18.(本题12分)已知直线经过点,且斜率为.
(Ⅰ)求直线的方程;(Ⅱ)求与直线切于点(2,2),圆心在直线上的圆的方程.
19.(本题12分)如图所示,在空间四边形ABCD中,E,F分别为AB,AD的中点,G,H分别在BC,CD上,且BG∶GC=DH∶HC=1∶2,求证: (1)E,F,G,H四点共面.
(2)EG与HF的交点在直线AC上.
20.(本题12分)求经过直线L1:3x + 4y – 5 = 0与直线L2:2x – 3y + 8 = 0的交点M,且满足下列条件的直线方程
(1)与直线2x + y + 5 = 0平行 ; (2)与直线2x + y + 5 = 0垂直;
21.(本题12分)如图所示,在直三棱柱中,,,、分别为、的中点.
(Ⅰ)求证:; (Ⅱ)求证:.
22.(本题12分)已知圆的方程为:.
(1)试求的值,使圆的面积最小;
(2)求与满足(1)中条件的圆相切,且过点的直线方程.
答案
高一数学 命题人:
一.选择题(本大题共12道小题,每小题5分,共60分)
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 A C D C D A D B B B C B
二.填空题(本大题共4道小题,每小题5分,共20分)
14.
15.4 圆锥 16.①②④
三.解答题
17.PO⊥☉O,CA?平面☉O,
所以OP⊥AC.
因为AD=CD,所以OD⊥AC.
因为OP∩OD=O,
所以AC⊥平面POD.
因为AC?平面PAC,
所以平面POD⊥平面PAC...........(10)
18.(Ⅰ)由直线方程的点斜式,得
整理,得所求直线方程为 ……………4分
(Ⅱ)过点(2,2)与垂直的直线方程为, ……………6分
由得圆心为(5,6), ……………8分
∴半径, ……………10分
故所求圆的方程为. ………12分
19.(1)因为BG∶GC=DH∶HC=1∶2,
所以GH∥BD,
因为E,F分别为AB,AD的中点,
所以EF∥BD,所以EF∥GH,
所以E,F,G,H四点共面......................6分
(2)因为G,H不是BC,CD的中点,
所以EF∥GH,且EF≠GH,
所以EG与FH必相交,设交点为M,
因为EG?平面ABC,HG?平面ACD,
所以M∈平面ABC,且M∈平面ACD,
因为平面ABC∩平面ACD=AC,
所以M∈AC,
所以EG与HF的交点在直线AC上......................12分
20.解:解得--------4分
所以交点(-1,2)
(1)-----6分
直线方程为--------8分
(2)---------10分
直线方程为--------12分
21.解析:(Ⅰ)在直三棱柱中,
侧面⊥底面,且侧面∩底面=,
∵∠=90°,即,
∴平面
∵平面,∴. ……4分
∵,,∴是正方形,
∴,∴. …………… 6分
(Ⅱ)取的中点,连、. ………………8分
在△中,、是中点,
∴,,又∵,,∴,,………6分
故四边形是平行四边形,∴,…………10分
而 面,平面,∴面 ……12分
22.配方得圆的方程:
(1)当时,圆的半径有最小值1,此时圆的面积最小。
(2)当时,圆的方程为
设所求的直线方程为
即
由直线与圆相切,得,
所以切线方程为,即
又过点且与轴垂直的直线与圆也相切
所发所求的切线方程为与。
同课章节目录
