第六章 1.1构成空间几何体的基本元素-【新教材】北师大版(2019)高中数学必修第二册课件23张PPT
文档属性
| 名称 | 第六章 1.1构成空间几何体的基本元素-【新教材】北师大版(2019)高中数学必修第二册课件23张PPT |

|
|
| 格式 | ppt | ||
| 文件大小 | 750.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-20 00:00:00 | ||
图片预览








文档简介
1.1 构成空间几何体的基本元素
课标阐释
1.借助几何体,理解点、线、面是构成几何体的基本元素.(数学抽象)
2.平面的特征性质及其表示.(数学抽象)
3.初步了解空间中直线与直线、直线与平面、平面与平面间的位置关系.(几何直观)
思维脉络
激趣诱思
知识点拨
在现实生活中,有很多自然现象值得我们深入思考,也有一些生活细节需要大家用心体会.夜晚一颗流星突然划破长空,形成一道美丽的弧线;雨雪天气中行驶的汽车,不时地转动着雨刷;清晨起床后洗漱挤出的牙膏……看似风马牛不相及的事物,其实都包含着“点动成线”“线动成面”“面动成体”的数学规律.构成空间几何体的基本元素你找到了吗?
激趣诱思
知识点拨
一、构成空间几何体的基本元素
空间几何体的基本几何元素是点、线(直线和曲线)、面(平面和曲面)等.
名师点析1.我们所学的几何体只考虑一个物体占有空间部分的形状和大小,而不考虑其他因素.
2.以长方体为例:长方体由六个面围成,每个面都是矩形(包括它的内部);相邻两个面的公共边,叫作长方体的棱;棱和棱的公共点,叫作长方体的顶点.长方体有6个面、12条棱、8个顶点.
3.从运动的角度理解点、线、面,“点动成线”“线动成面”“面动成体”.
激趣诱思
知识点拨
微思考
天空中飘浮的气球是空间几何体吗?它是否由点、线、面构成?
提示气球的内部虽是空的,但气球仍占有一定的空间,具有大小和形状,因此气球是空间几何体,它也是由点、线、面构成的.
微练习
下列不属于构成几何体的基本元素的是( )
A.点 B.线
C.曲面 D.多边形(不含内部的点)
解析本题考查了构成空间几何体的基本元素,关键是对概念的理解.由于一个几何体是由点、线、面组成的,而线有直线和曲线之分,面有平面和曲面之分,故而只有D不属于构成几何体的基本元素,故选D.
答案D
激趣诱思
知识点拨
二、平面
1.特征:平面是空间最基本的图形,平面是无限延展的.
2.画法:一般地,用平行四边形表示平面,当平面水平放置时,通常把平行四边形的锐角画成45°,横边长画成邻边长的两倍.
3.命名:平面通常用希腊字母α,β,γ等来表示,也可以用表示平行四边形顶点的字母表示,还可以用表示平行四边形顶点的两个相对顶点的字母表示.
名师点析1.平面是只描述不定义的原始概念,它具有无限延展性,是理想的、处处平直的,因此它没有厚度、没有大小,也没有面积、体积、重量等,即平面在各个项目上都是不可度量的.
2.平面的无限延展性,使其能将空间一分为二,也正是由于它的无限延展性,可以根据我们的需要向四周延展.
激趣诱思
知识点拨
微练习
(多选)下列说法中正确的是( )
A.平面是由空间点、线组成的无限集合
B.平静的太平洋面是平面
C.平面就是平行四边形
D.平面多边形和圆、椭圆都可以用来表示平面
解析本题考查平面的描述性定义和平面的性质.A正确,根据平面的特征可知正确;B不正确,太平洋面即使再平静也不是平的(因为地球是圆的),更不可能是无限延展的;C不正确,平面是无限延展的,我们一般用平行四边形来表示平面;D正确,它符合平面表示方法的规定.
答案AD
激趣诱思
知识点拨
三、空间中直线、平面的位置关系
如图,直线AB和平面A1B1C1D1没有公共点,即直线AB与平面A1B1C1D1平行;直线AA1和平面ABCD 中的AD,AB均垂直,可以看作AA1垂直于平面ABCD;平面ABCD和平面A1B1C1D1没有公共点,我们说这两个平面是平行的;平面ABCD和平面A1ABB1反映了两个平面相交.
激趣诱思
知识点拨
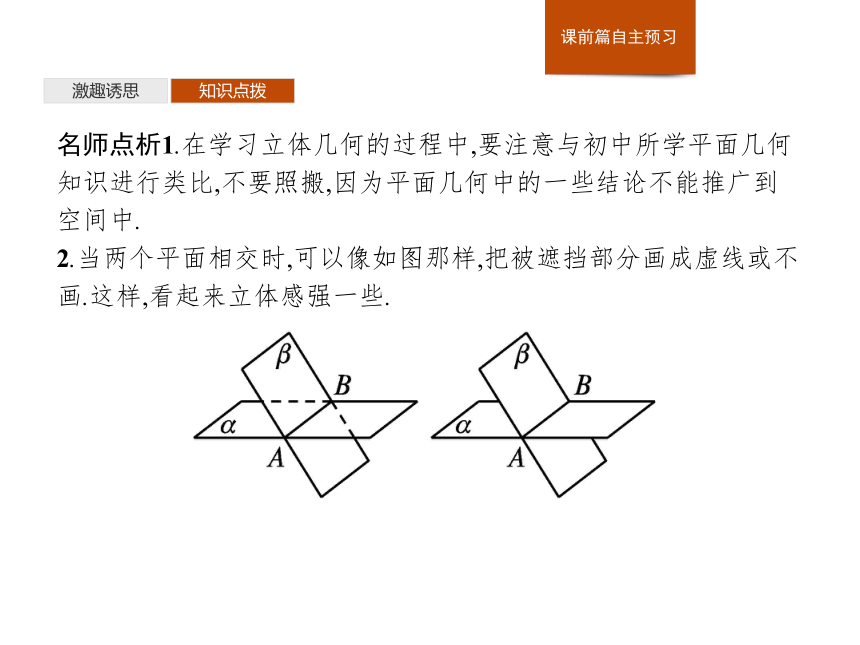
名师点析1.在学习立体几何的过程中,要注意与初中所学平面几何知识进行类比,不要照搬,因为平面几何中的一些结论不能推广到空间中.
2.当两个平面相交时,可以像如图那样,把被遮挡部分画成虚线或不画.这样,看起来立体感强一些.
激趣诱思
知识点拨
微练习1
在正方体ABCD-A1B1C1D1中,与对角线BD1既不相交又不平行的棱有( )
A.3条 B.4条 C.6条 D.8条
答案C
微练习2
下列关于长方体ABCD-A1B1C1D1中点、线、面位置关系的说法正确的是 .(填序号)?
①直线AA1与直线BB1平行;
②直线AA1与平面C1D1DC相交;
③直线AA1与平面ABCD垂直;
④点A1与点B1到平面ABCD的距离相等.
答案①③④
探究一
探究二
探究三
当堂检测
构成几何体的基本元素
例1试指出下图中组成各几何体的基本元素.
解(1)中几何体有6个顶点、12条棱和8个面.
(2)中几何体有12个顶点、18条棱和8个面.
(3)中几何体有6个顶点、10条棱和6个面.
探究一
探究二
探究三
当堂检测
反思感悟 点是最基本的元素,只有位置,没有大小;直线没有粗细,向两方无限延伸;平面没有厚度,向四周无限延展.要熟记这三种基本元素的特点.在现实生活中要多观察几何体,以便加深对构成空间几何体的基本元素的认识.
探究一
探究二
探究三
当堂检测
变式训练1如图,在长方体ABCD-A1B1C1D1中,下列说法正确的有 .(填序号)?
①长方体一共有8个顶点;
②线段AA1所在的直线是长方体的一条棱;
③矩形ABCD所在的平面是长方体的一个面;
④长方体由六个平面围成.
答案①
探究一
探究二
探究三
当堂检测
对于平面的理解
例2判断下列说法是否正确,并说明理由.
(1)平面的形状是平行四边形;
(2)圆和平面多边形都可以表示平面;
(3)若S?ABCD>S?A'B'C'D',则平面ABCD大于平面A'B'C'D'.
解(1)不正确.我们常用平行四边形表示平面,但不能说平面的形状是平行四边形,平面是无形状可言的.
(2)正确.通常情况下我们利用平行四边形来表示平面,但有时根据需要也可以用圆或其他平面多边形来表示平面.
(3)不正确.因为平面无大小可言.
探究一
探究二
探究三
当堂检测
反思感悟 1.在空间几何体中,平面是无限延展的,是理想的、绝对平直的.
2.平面是抽象出来的,没有厚度、没有大小,因此无法度量.平面几何中的平面图形,如三角形、四边形等都是有大小的,可以度量的,它们本身不是平面.
3.任何一个平面都可以将空间分为两部分,如果想从平面的一侧到另一侧,那么必须穿过这个平面.
探究一
探究二
探究三
当堂检测
变式训练2下列说法正确的是( )
A.生活中的几何体都是由平面组成的
B.曲面都是有一定大小的
C.直线是无限个点组成的,而线段是由有限个点组成的
D.平面图形是空间图形的重要组成部分
解析组成几何体的面既可以是平面,也可以是曲面;曲面也可以是无限延展的;直线和线段都是由无数个点组成的.根据这些特点可以排除A,B,C.
答案D
探究一
探究二
探究三
当堂检测
几何中基本元素的位置关系
例3如图所示的长方体ABCD-A1B1C1D1,在长方体的面与棱中,
(1)与棱BC平行的棱是哪几条?
(2)与棱BC平行的平面是哪几个?
(3)与棱BC垂直的平面是哪几个?
(4)与平面BC1垂直的平面是哪几个?
解在长方体的面与棱中,
(1)与棱BC平行的棱有棱B1C1,棱A1D1,棱AD.
(2)与棱BC平行的平面有平面A1C1,平面AD1.
(3)与棱BC垂直的平面有平面AB1,平面DC1.
(4)与平面BC1垂直的平面有平面AB1,平面A1C1,平面DC1,平面AC.
探究一
探究二
探究三
当堂检测
反思感悟 通过本例可以得到如下规律:
1.平行关系
(1)直线与直线的平行关系:
如图,在长方体的12条棱中,分成“长”“宽”“高”三组,
其中“高”AA1,BB1,CC1,DD1相互平行;“长”AB,DC,
A1B1,D1C1相互平行;“宽”AD,BC,A1D1,B1C1相互平行.
(2)直线与平面的平行关系:
在长方体的12条棱及表面中,若棱所在的直线与某一平面(棱不在该平面内)不相交,则二者平行.
(3)平面与平面的平行关系:长方体的对面相互平行.
探究一
探究二
探究三
当堂检测
2.垂直关系
(1)直线与平面的垂直关系:
在长方体的棱所在直线与各表面中,若直线与平面有且只有一个公共点,则二者垂直.
(2)平面与平面的垂直关系:
在长方体的各表面中,若两平面有公共点,则二者垂直.
探究一
探究二
探究三
当堂检测
延伸探究(1)本例中与棱A1D1相交的棱有哪几条?它们与棱A1D1所成的角的度数是多少?
(2)在本例长方体的12条棱中,可以用来表示面A1B与面D1C之间距离的是哪些棱长?
解(1)与棱A1D1相交的棱有4条,分别是棱A1A,棱A1B1,棱D1D,棱D1C1.因为长方体六个面都是矩形,所以它们与棱A1D1所成的角的度数都是90°.
(2)由长方体的性质知棱A1D1,棱B1C1,棱BC,棱AD的长都可以用来表示面A1B与面D1C之间的距离.
探究一
探究二
探究三
当堂检测
1.给出以下说法:
①铺得很平的一张白纸是一个平面;②一个平面的面积是6 cm2;③平行四边形是一个平面;④任何一个平面图形都是一个平面;⑤平面多边形和圆都可以用来表示平面.
其中正确说法的个数是( )
A.0 B.1 C.2 D.3
解析由平面的概念知⑤正确,其余说法均错误.
答案B
探究一
探究二
探究三
当堂检测
2.下列说法正确的是( )
A.在空间中,一个点运动成直线
B.在空间中,直线平行移动形成平面
C.在空间中,直线绕与其相交的另一条直线转动形成平面或锥面
D.在空间中,矩形上各点沿同一方向移动形成长方体
解析一个点运动也可以成曲线,故A错;在空间中,直线平行移动可以形成平面或曲面,故B错;在空间中,矩形上各点沿铅垂线向上(或向下)移动相同距离所形成的几何体是长方体,故D错.
答案C
探究一
探究二
探究三
当堂检测
3.如图是一个正方体的表面展开图,A,B,C均为所在棱的中点,D为正方体的顶点.若正方体的棱长为2,求封闭折线ABCDA的长.
课标阐释
1.借助几何体,理解点、线、面是构成几何体的基本元素.(数学抽象)
2.平面的特征性质及其表示.(数学抽象)
3.初步了解空间中直线与直线、直线与平面、平面与平面间的位置关系.(几何直观)
思维脉络
激趣诱思
知识点拨
在现实生活中,有很多自然现象值得我们深入思考,也有一些生活细节需要大家用心体会.夜晚一颗流星突然划破长空,形成一道美丽的弧线;雨雪天气中行驶的汽车,不时地转动着雨刷;清晨起床后洗漱挤出的牙膏……看似风马牛不相及的事物,其实都包含着“点动成线”“线动成面”“面动成体”的数学规律.构成空间几何体的基本元素你找到了吗?
激趣诱思
知识点拨
一、构成空间几何体的基本元素
空间几何体的基本几何元素是点、线(直线和曲线)、面(平面和曲面)等.
名师点析1.我们所学的几何体只考虑一个物体占有空间部分的形状和大小,而不考虑其他因素.
2.以长方体为例:长方体由六个面围成,每个面都是矩形(包括它的内部);相邻两个面的公共边,叫作长方体的棱;棱和棱的公共点,叫作长方体的顶点.长方体有6个面、12条棱、8个顶点.
3.从运动的角度理解点、线、面,“点动成线”“线动成面”“面动成体”.
激趣诱思
知识点拨
微思考
天空中飘浮的气球是空间几何体吗?它是否由点、线、面构成?
提示气球的内部虽是空的,但气球仍占有一定的空间,具有大小和形状,因此气球是空间几何体,它也是由点、线、面构成的.
微练习
下列不属于构成几何体的基本元素的是( )
A.点 B.线
C.曲面 D.多边形(不含内部的点)
解析本题考查了构成空间几何体的基本元素,关键是对概念的理解.由于一个几何体是由点、线、面组成的,而线有直线和曲线之分,面有平面和曲面之分,故而只有D不属于构成几何体的基本元素,故选D.
答案D
激趣诱思
知识点拨
二、平面
1.特征:平面是空间最基本的图形,平面是无限延展的.
2.画法:一般地,用平行四边形表示平面,当平面水平放置时,通常把平行四边形的锐角画成45°,横边长画成邻边长的两倍.
3.命名:平面通常用希腊字母α,β,γ等来表示,也可以用表示平行四边形顶点的字母表示,还可以用表示平行四边形顶点的两个相对顶点的字母表示.
名师点析1.平面是只描述不定义的原始概念,它具有无限延展性,是理想的、处处平直的,因此它没有厚度、没有大小,也没有面积、体积、重量等,即平面在各个项目上都是不可度量的.
2.平面的无限延展性,使其能将空间一分为二,也正是由于它的无限延展性,可以根据我们的需要向四周延展.
激趣诱思
知识点拨
微练习
(多选)下列说法中正确的是( )
A.平面是由空间点、线组成的无限集合
B.平静的太平洋面是平面
C.平面就是平行四边形
D.平面多边形和圆、椭圆都可以用来表示平面
解析本题考查平面的描述性定义和平面的性质.A正确,根据平面的特征可知正确;B不正确,太平洋面即使再平静也不是平的(因为地球是圆的),更不可能是无限延展的;C不正确,平面是无限延展的,我们一般用平行四边形来表示平面;D正确,它符合平面表示方法的规定.
答案AD
激趣诱思
知识点拨
三、空间中直线、平面的位置关系
如图,直线AB和平面A1B1C1D1没有公共点,即直线AB与平面A1B1C1D1平行;直线AA1和平面ABCD 中的AD,AB均垂直,可以看作AA1垂直于平面ABCD;平面ABCD和平面A1B1C1D1没有公共点,我们说这两个平面是平行的;平面ABCD和平面A1ABB1反映了两个平面相交.
激趣诱思
知识点拨
名师点析1.在学习立体几何的过程中,要注意与初中所学平面几何知识进行类比,不要照搬,因为平面几何中的一些结论不能推广到空间中.
2.当两个平面相交时,可以像如图那样,把被遮挡部分画成虚线或不画.这样,看起来立体感强一些.
激趣诱思
知识点拨
微练习1
在正方体ABCD-A1B1C1D1中,与对角线BD1既不相交又不平行的棱有( )
A.3条 B.4条 C.6条 D.8条
答案C
微练习2
下列关于长方体ABCD-A1B1C1D1中点、线、面位置关系的说法正确的是 .(填序号)?
①直线AA1与直线BB1平行;
②直线AA1与平面C1D1DC相交;
③直线AA1与平面ABCD垂直;
④点A1与点B1到平面ABCD的距离相等.
答案①③④
探究一
探究二
探究三
当堂检测
构成几何体的基本元素
例1试指出下图中组成各几何体的基本元素.
解(1)中几何体有6个顶点、12条棱和8个面.
(2)中几何体有12个顶点、18条棱和8个面.
(3)中几何体有6个顶点、10条棱和6个面.
探究一
探究二
探究三
当堂检测
反思感悟 点是最基本的元素,只有位置,没有大小;直线没有粗细,向两方无限延伸;平面没有厚度,向四周无限延展.要熟记这三种基本元素的特点.在现实生活中要多观察几何体,以便加深对构成空间几何体的基本元素的认识.
探究一
探究二
探究三
当堂检测
变式训练1如图,在长方体ABCD-A1B1C1D1中,下列说法正确的有 .(填序号)?
①长方体一共有8个顶点;
②线段AA1所在的直线是长方体的一条棱;
③矩形ABCD所在的平面是长方体的一个面;
④长方体由六个平面围成.
答案①
探究一
探究二
探究三
当堂检测
对于平面的理解
例2判断下列说法是否正确,并说明理由.
(1)平面的形状是平行四边形;
(2)圆和平面多边形都可以表示平面;
(3)若S?ABCD>S?A'B'C'D',则平面ABCD大于平面A'B'C'D'.
解(1)不正确.我们常用平行四边形表示平面,但不能说平面的形状是平行四边形,平面是无形状可言的.
(2)正确.通常情况下我们利用平行四边形来表示平面,但有时根据需要也可以用圆或其他平面多边形来表示平面.
(3)不正确.因为平面无大小可言.
探究一
探究二
探究三
当堂检测
反思感悟 1.在空间几何体中,平面是无限延展的,是理想的、绝对平直的.
2.平面是抽象出来的,没有厚度、没有大小,因此无法度量.平面几何中的平面图形,如三角形、四边形等都是有大小的,可以度量的,它们本身不是平面.
3.任何一个平面都可以将空间分为两部分,如果想从平面的一侧到另一侧,那么必须穿过这个平面.
探究一
探究二
探究三
当堂检测
变式训练2下列说法正确的是( )
A.生活中的几何体都是由平面组成的
B.曲面都是有一定大小的
C.直线是无限个点组成的,而线段是由有限个点组成的
D.平面图形是空间图形的重要组成部分
解析组成几何体的面既可以是平面,也可以是曲面;曲面也可以是无限延展的;直线和线段都是由无数个点组成的.根据这些特点可以排除A,B,C.
答案D
探究一
探究二
探究三
当堂检测
几何中基本元素的位置关系
例3如图所示的长方体ABCD-A1B1C1D1,在长方体的面与棱中,
(1)与棱BC平行的棱是哪几条?
(2)与棱BC平行的平面是哪几个?
(3)与棱BC垂直的平面是哪几个?
(4)与平面BC1垂直的平面是哪几个?
解在长方体的面与棱中,
(1)与棱BC平行的棱有棱B1C1,棱A1D1,棱AD.
(2)与棱BC平行的平面有平面A1C1,平面AD1.
(3)与棱BC垂直的平面有平面AB1,平面DC1.
(4)与平面BC1垂直的平面有平面AB1,平面A1C1,平面DC1,平面AC.
探究一
探究二
探究三
当堂检测
反思感悟 通过本例可以得到如下规律:
1.平行关系
(1)直线与直线的平行关系:
如图,在长方体的12条棱中,分成“长”“宽”“高”三组,
其中“高”AA1,BB1,CC1,DD1相互平行;“长”AB,DC,
A1B1,D1C1相互平行;“宽”AD,BC,A1D1,B1C1相互平行.
(2)直线与平面的平行关系:
在长方体的12条棱及表面中,若棱所在的直线与某一平面(棱不在该平面内)不相交,则二者平行.
(3)平面与平面的平行关系:长方体的对面相互平行.
探究一
探究二
探究三
当堂检测
2.垂直关系
(1)直线与平面的垂直关系:
在长方体的棱所在直线与各表面中,若直线与平面有且只有一个公共点,则二者垂直.
(2)平面与平面的垂直关系:
在长方体的各表面中,若两平面有公共点,则二者垂直.
探究一
探究二
探究三
当堂检测
延伸探究(1)本例中与棱A1D1相交的棱有哪几条?它们与棱A1D1所成的角的度数是多少?
(2)在本例长方体的12条棱中,可以用来表示面A1B与面D1C之间距离的是哪些棱长?
解(1)与棱A1D1相交的棱有4条,分别是棱A1A,棱A1B1,棱D1D,棱D1C1.因为长方体六个面都是矩形,所以它们与棱A1D1所成的角的度数都是90°.
(2)由长方体的性质知棱A1D1,棱B1C1,棱BC,棱AD的长都可以用来表示面A1B与面D1C之间的距离.
探究一
探究二
探究三
当堂检测
1.给出以下说法:
①铺得很平的一张白纸是一个平面;②一个平面的面积是6 cm2;③平行四边形是一个平面;④任何一个平面图形都是一个平面;⑤平面多边形和圆都可以用来表示平面.
其中正确说法的个数是( )
A.0 B.1 C.2 D.3
解析由平面的概念知⑤正确,其余说法均错误.
答案B
探究一
探究二
探究三
当堂检测
2.下列说法正确的是( )
A.在空间中,一个点运动成直线
B.在空间中,直线平行移动形成平面
C.在空间中,直线绕与其相交的另一条直线转动形成平面或锥面
D.在空间中,矩形上各点沿同一方向移动形成长方体
解析一个点运动也可以成曲线,故A错;在空间中,直线平行移动可以形成平面或曲面,故B错;在空间中,矩形上各点沿铅垂线向上(或向下)移动相同距离所形成的几何体是长方体,故D错.
答案C
探究一
探究二
探究三
当堂检测
3.如图是一个正方体的表面展开图,A,B,C均为所在棱的中点,D为正方体的顶点.若正方体的棱长为2,求封闭折线ABCDA的长.
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
