第六章 4.2平面与平面平行-【新教材】北师大版(2019)高中数学必修第二册课件24张PPT
文档属性
| 名称 | 第六章 4.2平面与平面平行-【新教材】北师大版(2019)高中数学必修第二册课件24张PPT |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-20 00:00:00 | ||
图片预览








文档简介
4.2 平面与平面平行
课标阐释
1.理解平面与平面平行的性质定理的含义,并能用图形语言、文字语言、符号语言进行描述.(几何直观、数学抽象)
2.理解平面与平面平行的判定定理的含义,并能用图形语言、文字语言、符号语言进行描述.(几何直观、数学抽象)
3.能运用平面与平面平行的性质定理和平面与平面平行的判定定理证明一些空间中相关的平行问题.(逻辑推理)
思维脉络
激趣诱思
知识点拨
《老子》中说:上善若水,水善利万物而不争.一滴水,可方可圆,泽润万物;一个人,能方能圆,方圆相济,便可活得豁达、圆满.方中有圆,圆中有方,是大自然的规律,也是为人处世的准则.“天行健,君子以自强不息;地势坤,君子以厚德载物”,在这里,圆是天地周而复始运转不息的象征,方是大地之旷远宽厚稳重的象征.我国古代的钱币,外部是圆形,内部是方孔,看似朴实无华,但蕴含着古人智慧和人生哲理.我们学习过的旋转体圆柱就蕴含着长方形的截面,它是如何得到的?能否用数学原理解释截面的形状?
激趣诱思
知识点拨
一、平面与平面平行的性质定理
文字语言
两个平面平行,如果另一个平面与这两个平面相交,那么两条交线平行
图形语言
?
符号语言
α∥β,α∩γ=a,β∩γ=b?a∥b
作用
证明两条直线平行
激趣诱思
知识点拨
名师点析正确理解面面平行的性质定理
(1)面面平行的性质定理可以作为证明线线平行的一种方法.
(2)已知两个平面平行,虽然一个平面内的任何直线都平行于另一个平面,但是这两个平面内的所有直线并不一定相互平行.
(3)面面平行的其他性质:
①在两个平行平面中,一个平面内的直线必平行于另一个平面.即“面面平行,则线面平行”.这可以作为证明线面平行的一种方法.
②夹在两个平行平面间的平行线段相等.
③如果两个平面都与第三个平面平行,那么这两个平面互相平行.
④两条直线被三个平行平面所截,截得的对应线段成比例.
⑤经过平面外一点有且只有一个平面与已知平面平行.
激趣诱思
知识点拨
微判断
判断(正确的打“√”,错误的打“×”).
(1)若三个平面α,β,γ满足α∥β∥γ,且平面δ与这三个平面相交,交线分别为a,b,c,则有a∥b∥c成立.( )
(2)若直线a?平面α,直线b?平面β,且α∥β,则a,b无交点.( )
(3)若平面α∥平面β,且a?α,b?β,则a∥b.( )
答案(1)√ (2)√ (3)×
激趣诱思
知识点拨
微练习
已知平面α∥平面β,平面γ∥平面δ,且α∩γ=a,α∩δ=b,β∩γ=c,β∩δ=d,则交线a,b,c,d的位置关系是( )
A.互相平行
B.交于一点
C.相互异面
D.不能确定
解析由面面平行的性质定理,可知答案为A.
答案A
激趣诱思
知识点拨
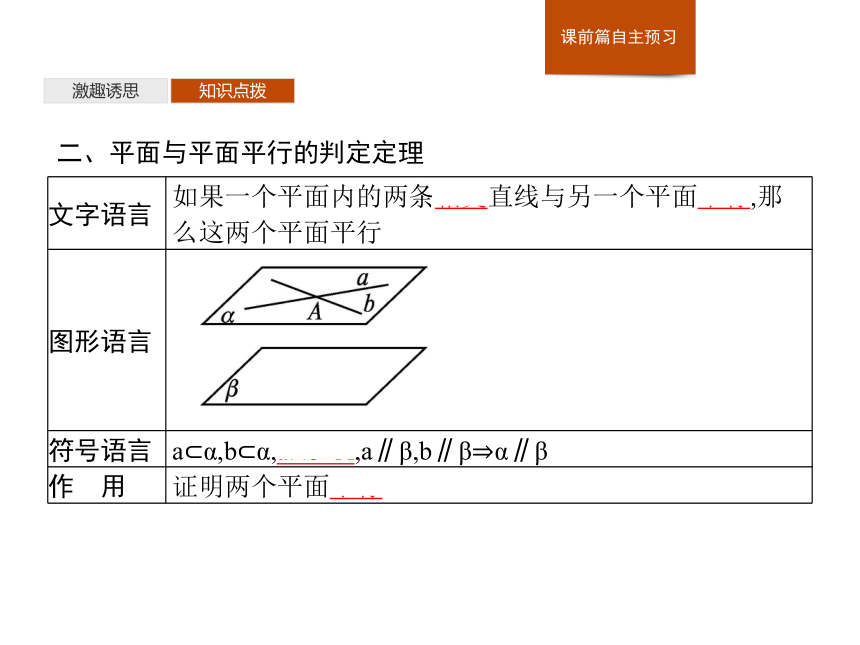
二、平面与平面平行的判定定理
文字语言
如果一个平面内的两条相交直线与另一个平面平行,那么这两个平面平行
图形语言
?
符号语言
a?α,b?α,a∩b=A,a∥β,b∥β?α∥β
作 用
证明两个平面平行
激趣诱思
知识点拨
名师点析应用面面平行判定定理应具备的条件
(1)平面α内两条相交直线a,b,即a?α,b?α,a∩b=A.
(2)两条相交直线a,b都与β平行,即a∥β,b∥β.
微思考
使三角板的一条边所在直线与桌面平行,这个三角板所在的平面与桌面平行吗?
提示不一定,也可能相交.
激趣诱思
知识点拨
微判断
判断(正确的打“√”,错误的打“×”).
(1)若一个平面内的两条直线都与另一个平面平行,则这两个平面平行.( )
(2)直线a∥平面β,直线b∥平面β,a?平面α,b?平面α?平面α∥平面β.( )
答案(1)× (2)×
激趣诱思
知识点拨
微练习
若一个平面内的两条直线分别平行于另一个平面内的两条直线,则这两个平面的位置关系是( )
A.一定平行 B.一定相交
C.平行或相交 D.以上都不对
解析当每个平面内的两条直线都是相交直线时,可推出两个平面一定平行.否则,两个平面有可能相交.
答案C
探究一
探究二
探究三
当堂检测
平面与平面平行的性质定理的应用
例1如图,已知平面α∥平面β,点P是平面α,β外的一点(不在α与β之间),直线PB,PD分别与α,β相交于点A,B和C,D.
(1)求证:AC∥BD;
(2)已知PA=4,AB=5,PC=3,求PD的长.
(1)证明因为PB∩PD=P,
所以直线PB和PD确定一个平面γ,
则α∩γ=AC,β∩γ=BD.又α∥β,所以AC∥BD.
(2)解由(1)得AC∥BD,
探究一
探究二
探究三
当堂检测
反思感悟 证明线线平行的方法
(1)定义法:在同一个平面内没有公共点的两条直线平行.
(2)平行公理:平行于同一条直线的两条直线平行.
探究一
探究二
探究三
当堂检测
延伸探究在本例中,若P在α与β之间,在第(2)问条件下求CD的长.
解如图,因为PB∩PC=P,
所以PB,PC确定平面γ,γ∩α=AC,γ∩β=BD.
又α∥β,所以AC∥BD,所以△PAC∽△PBD,
探究一
探究二
探究三
当堂检测
平面与平面平行的判定定理的应用
例2如图,在四棱锥P-ABCD中,E,F,G分别是PC,PD,BC的中点,DC∥AB,求证:平面PAB∥平面EFG.
证明因为E,G分别是PC,BC的中点,所以EG∥PB.
又因为EG?平面PAB,PB?平面PAB,所以EG∥平面PAB.
因为E,F分别是PC,PD的中点,所以EF∥CD.
又因为AB∥CD,所以EF∥AB.
因为EF?平面PAB,AB?平面PAB,
所以EF∥平面PAB,又EF∩EG=E,EF?平面EFG,EG?平面EFG,所以平面EFG∥平面PAB.
探究一
探究二
探究三
当堂检测
反思感悟 证明两个平面平行,可以用定义,也可以用判定定理.但用定义证明时,需说明两个平面没有公共点,这一点也不容易做到(可用反证法),所以通常用判定定理证明两个平面平行,其步骤如下:
探究一
探究二
探究三
当堂检测
变式训练如图,在三棱柱ABC-A1B1C1中,E,F,G,H分别是AB,AC,A1B1,A1C1的中点.
求证:(1)B,C,H,G四点共面;
(2)平面EFA1∥平面BCHG.
探究一
探究二
探究三
当堂检测
证明(1)因为GH是△A1B1C1的中位线,所以GH∥B1C1.
又B1C1∥BC,所以GH∥BC,
所以B,C,H,G四点共面.
(2)因为E,F分别为AB,AC的中点,所以EF∥BC.
因为EF?平面BCHG,BC?平面BCHG,
所以EF∥平面BCHG.
因为A1G∥EB,且A1G=EB,
所以四边形A1EBG是平行四边形,所以A1E∥GB.
因为A1E?平面BCHG,GB?平面BCHG,
所以A1E∥平面BCHG.
因为A1E∩EF=E,A1E?平面EFA1,EF?平面EFA1,
所以平面EFA1∥平面BCHG.
探究一
探究二
探究三
当堂检测
线面平行、面面平行的综合问题
例3如图所示,在三棱柱ABC-A1B1C1中,平面ABC∥平面A1B1C1.若D是棱CC1的中点,在棱AB上是否存在一点E,使DE∥平面AB1C1?证明你的结论.
探究一
探究二
探究三
当堂检测
解当E为棱AB的中点时,DE∥平面AB1C1.
证明如下:
如图所示,取BB1的中点F,连接EF,FD,DE.
因为D,E,F分别为CC1,AB,BB1的中点,所以EF∥AB1.
因为AB1?平面AB1C1,EF?平面AB1C1,
所以EF∥平面AB1C1.
同理可证FD∥平面AB1C1.
因为EF∩FD=F,所以平面EFD∥平面AB1C1.
因为DE?平面EFD,所以DE∥平面AB1C1.
探究一
探究二
探究三
当堂检测
反思感悟 1.证明直线与平面平行,除了定义法、判定定理法以外,还可以用两平面平行的性质,也就是说为了证明直线与平面平行,也可以先证明两平面平行,再由两平面平行的性质得到线面平行.
2.空间中线线、线面、面面平行关系的转化如下:
探究一
探究二
探究三
当堂检测
1.(2019全国Ⅱ高考)设α,β为两个平面,则α∥β的充要条件是( )
A.α内有无数条直线与β平行
B.α内有两条相交直线与β平行
C.α,β平行于同一条直线
D.α,β垂直于同一平面
解析由面面平行的判定定理知,“α内有两条相交直线与β平行”是“α∥β”的充分条件.由面面平行的性质知,“α内有两条相交直线与β平行”是“α∥β”的必要条件,故选B.
答案B
探究一
探究二
探究三
当堂检测
2.如图,在长方体ABCD-A1B1C1D1中,过BB1的中点E作一个与平面ACB1平行的平面交AB于点M,交BC于点N,则 = .?
解析因为平面MNE∥平面ACB1,
由平面平行的性质定理可得
EN∥B1C,EM∥B1A,
又因为E为BB1的中点,
所以M,N分别为BA,BC的中点,
探究一
探究二
探究三
当堂检测
3.如图所示,在正方体ABCD-A1B1C1D1中,求证:平面A1BD∥平面CD1B1.
证明由正方体性质可知,B1B∥D1D,且B1B=D1D,
所以四边形BB1D1D是平行四边形,所以D1B1∥DB.
又DB?平面A1BD,D1B1?平面A1BD,
所以D1B1∥平面A1BD.
同理B1C∥平面A1BD.
而B1C?平面CD1B1,B1D1?平面CD1B1,D1B1∩B1C=B1,所以平面A1BD∥平面CD1B1.
课标阐释
1.理解平面与平面平行的性质定理的含义,并能用图形语言、文字语言、符号语言进行描述.(几何直观、数学抽象)
2.理解平面与平面平行的判定定理的含义,并能用图形语言、文字语言、符号语言进行描述.(几何直观、数学抽象)
3.能运用平面与平面平行的性质定理和平面与平面平行的判定定理证明一些空间中相关的平行问题.(逻辑推理)
思维脉络
激趣诱思
知识点拨
《老子》中说:上善若水,水善利万物而不争.一滴水,可方可圆,泽润万物;一个人,能方能圆,方圆相济,便可活得豁达、圆满.方中有圆,圆中有方,是大自然的规律,也是为人处世的准则.“天行健,君子以自强不息;地势坤,君子以厚德载物”,在这里,圆是天地周而复始运转不息的象征,方是大地之旷远宽厚稳重的象征.我国古代的钱币,外部是圆形,内部是方孔,看似朴实无华,但蕴含着古人智慧和人生哲理.我们学习过的旋转体圆柱就蕴含着长方形的截面,它是如何得到的?能否用数学原理解释截面的形状?
激趣诱思
知识点拨
一、平面与平面平行的性质定理
文字语言
两个平面平行,如果另一个平面与这两个平面相交,那么两条交线平行
图形语言
?
符号语言
α∥β,α∩γ=a,β∩γ=b?a∥b
作用
证明两条直线平行
激趣诱思
知识点拨
名师点析正确理解面面平行的性质定理
(1)面面平行的性质定理可以作为证明线线平行的一种方法.
(2)已知两个平面平行,虽然一个平面内的任何直线都平行于另一个平面,但是这两个平面内的所有直线并不一定相互平行.
(3)面面平行的其他性质:
①在两个平行平面中,一个平面内的直线必平行于另一个平面.即“面面平行,则线面平行”.这可以作为证明线面平行的一种方法.
②夹在两个平行平面间的平行线段相等.
③如果两个平面都与第三个平面平行,那么这两个平面互相平行.
④两条直线被三个平行平面所截,截得的对应线段成比例.
⑤经过平面外一点有且只有一个平面与已知平面平行.
激趣诱思
知识点拨
微判断
判断(正确的打“√”,错误的打“×”).
(1)若三个平面α,β,γ满足α∥β∥γ,且平面δ与这三个平面相交,交线分别为a,b,c,则有a∥b∥c成立.( )
(2)若直线a?平面α,直线b?平面β,且α∥β,则a,b无交点.( )
(3)若平面α∥平面β,且a?α,b?β,则a∥b.( )
答案(1)√ (2)√ (3)×
激趣诱思
知识点拨
微练习
已知平面α∥平面β,平面γ∥平面δ,且α∩γ=a,α∩δ=b,β∩γ=c,β∩δ=d,则交线a,b,c,d的位置关系是( )
A.互相平行
B.交于一点
C.相互异面
D.不能确定
解析由面面平行的性质定理,可知答案为A.
答案A
激趣诱思
知识点拨
二、平面与平面平行的判定定理
文字语言
如果一个平面内的两条相交直线与另一个平面平行,那么这两个平面平行
图形语言
?
符号语言
a?α,b?α,a∩b=A,a∥β,b∥β?α∥β
作 用
证明两个平面平行
激趣诱思
知识点拨
名师点析应用面面平行判定定理应具备的条件
(1)平面α内两条相交直线a,b,即a?α,b?α,a∩b=A.
(2)两条相交直线a,b都与β平行,即a∥β,b∥β.
微思考
使三角板的一条边所在直线与桌面平行,这个三角板所在的平面与桌面平行吗?
提示不一定,也可能相交.
激趣诱思
知识点拨
微判断
判断(正确的打“√”,错误的打“×”).
(1)若一个平面内的两条直线都与另一个平面平行,则这两个平面平行.( )
(2)直线a∥平面β,直线b∥平面β,a?平面α,b?平面α?平面α∥平面β.( )
答案(1)× (2)×
激趣诱思
知识点拨
微练习
若一个平面内的两条直线分别平行于另一个平面内的两条直线,则这两个平面的位置关系是( )
A.一定平行 B.一定相交
C.平行或相交 D.以上都不对
解析当每个平面内的两条直线都是相交直线时,可推出两个平面一定平行.否则,两个平面有可能相交.
答案C
探究一
探究二
探究三
当堂检测
平面与平面平行的性质定理的应用
例1如图,已知平面α∥平面β,点P是平面α,β外的一点(不在α与β之间),直线PB,PD分别与α,β相交于点A,B和C,D.
(1)求证:AC∥BD;
(2)已知PA=4,AB=5,PC=3,求PD的长.
(1)证明因为PB∩PD=P,
所以直线PB和PD确定一个平面γ,
则α∩γ=AC,β∩γ=BD.又α∥β,所以AC∥BD.
(2)解由(1)得AC∥BD,
探究一
探究二
探究三
当堂检测
反思感悟 证明线线平行的方法
(1)定义法:在同一个平面内没有公共点的两条直线平行.
(2)平行公理:平行于同一条直线的两条直线平行.
探究一
探究二
探究三
当堂检测
延伸探究在本例中,若P在α与β之间,在第(2)问条件下求CD的长.
解如图,因为PB∩PC=P,
所以PB,PC确定平面γ,γ∩α=AC,γ∩β=BD.
又α∥β,所以AC∥BD,所以△PAC∽△PBD,
探究一
探究二
探究三
当堂检测
平面与平面平行的判定定理的应用
例2如图,在四棱锥P-ABCD中,E,F,G分别是PC,PD,BC的中点,DC∥AB,求证:平面PAB∥平面EFG.
证明因为E,G分别是PC,BC的中点,所以EG∥PB.
又因为EG?平面PAB,PB?平面PAB,所以EG∥平面PAB.
因为E,F分别是PC,PD的中点,所以EF∥CD.
又因为AB∥CD,所以EF∥AB.
因为EF?平面PAB,AB?平面PAB,
所以EF∥平面PAB,又EF∩EG=E,EF?平面EFG,EG?平面EFG,所以平面EFG∥平面PAB.
探究一
探究二
探究三
当堂检测
反思感悟 证明两个平面平行,可以用定义,也可以用判定定理.但用定义证明时,需说明两个平面没有公共点,这一点也不容易做到(可用反证法),所以通常用判定定理证明两个平面平行,其步骤如下:
探究一
探究二
探究三
当堂检测
变式训练如图,在三棱柱ABC-A1B1C1中,E,F,G,H分别是AB,AC,A1B1,A1C1的中点.
求证:(1)B,C,H,G四点共面;
(2)平面EFA1∥平面BCHG.
探究一
探究二
探究三
当堂检测
证明(1)因为GH是△A1B1C1的中位线,所以GH∥B1C1.
又B1C1∥BC,所以GH∥BC,
所以B,C,H,G四点共面.
(2)因为E,F分别为AB,AC的中点,所以EF∥BC.
因为EF?平面BCHG,BC?平面BCHG,
所以EF∥平面BCHG.
因为A1G∥EB,且A1G=EB,
所以四边形A1EBG是平行四边形,所以A1E∥GB.
因为A1E?平面BCHG,GB?平面BCHG,
所以A1E∥平面BCHG.
因为A1E∩EF=E,A1E?平面EFA1,EF?平面EFA1,
所以平面EFA1∥平面BCHG.
探究一
探究二
探究三
当堂检测
线面平行、面面平行的综合问题
例3如图所示,在三棱柱ABC-A1B1C1中,平面ABC∥平面A1B1C1.若D是棱CC1的中点,在棱AB上是否存在一点E,使DE∥平面AB1C1?证明你的结论.
探究一
探究二
探究三
当堂检测
解当E为棱AB的中点时,DE∥平面AB1C1.
证明如下:
如图所示,取BB1的中点F,连接EF,FD,DE.
因为D,E,F分别为CC1,AB,BB1的中点,所以EF∥AB1.
因为AB1?平面AB1C1,EF?平面AB1C1,
所以EF∥平面AB1C1.
同理可证FD∥平面AB1C1.
因为EF∩FD=F,所以平面EFD∥平面AB1C1.
因为DE?平面EFD,所以DE∥平面AB1C1.
探究一
探究二
探究三
当堂检测
反思感悟 1.证明直线与平面平行,除了定义法、判定定理法以外,还可以用两平面平行的性质,也就是说为了证明直线与平面平行,也可以先证明两平面平行,再由两平面平行的性质得到线面平行.
2.空间中线线、线面、面面平行关系的转化如下:
探究一
探究二
探究三
当堂检测
1.(2019全国Ⅱ高考)设α,β为两个平面,则α∥β的充要条件是( )
A.α内有无数条直线与β平行
B.α内有两条相交直线与β平行
C.α,β平行于同一条直线
D.α,β垂直于同一平面
解析由面面平行的判定定理知,“α内有两条相交直线与β平行”是“α∥β”的充分条件.由面面平行的性质知,“α内有两条相交直线与β平行”是“α∥β”的必要条件,故选B.
答案B
探究一
探究二
探究三
当堂检测
2.如图,在长方体ABCD-A1B1C1D1中,过BB1的中点E作一个与平面ACB1平行的平面交AB于点M,交BC于点N,则 = .?
解析因为平面MNE∥平面ACB1,
由平面平行的性质定理可得
EN∥B1C,EM∥B1A,
又因为E为BB1的中点,
所以M,N分别为BA,BC的中点,
探究一
探究二
探究三
当堂检测
3.如图所示,在正方体ABCD-A1B1C1D1中,求证:平面A1BD∥平面CD1B1.
证明由正方体性质可知,B1B∥D1D,且B1B=D1D,
所以四边形BB1D1D是平行四边形,所以D1B1∥DB.
又DB?平面A1BD,D1B1?平面A1BD,
所以D1B1∥平面A1BD.
同理B1C∥平面A1BD.
而B1C?平面CD1B1,B1D1?平面CD1B1,D1B1∩B1C=B1,所以平面A1BD∥平面CD1B1.
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
