第六章 5.1直线与平面垂直-【新教材】北师大版(2019)高中数学必修第二册课件36张PPT
文档属性
| 名称 | 第六章 5.1直线与平面垂直-【新教材】北师大版(2019)高中数学必修第二册课件36张PPT |  | |
| 格式 | ppt | ||
| 文件大小 | 967.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-20 18:29:38 | ||
图片预览








文档简介
5.1 直线与平面垂直
课标阐释
1.借助常见几何体了解直线与平面垂直的定义,了解直线与平面所成角的概念.(数学抽象,几何直观)
2.掌握直线与平面垂直的性质定理,并会用定理证明相关问题.(逻辑推理)
3.掌握直线与平面垂直的判定定理,并会用定理判定线面垂直.(逻辑推理)
4.会求简单的空间距离问题(点面距离、线面距离、面面距离).(数学运算)
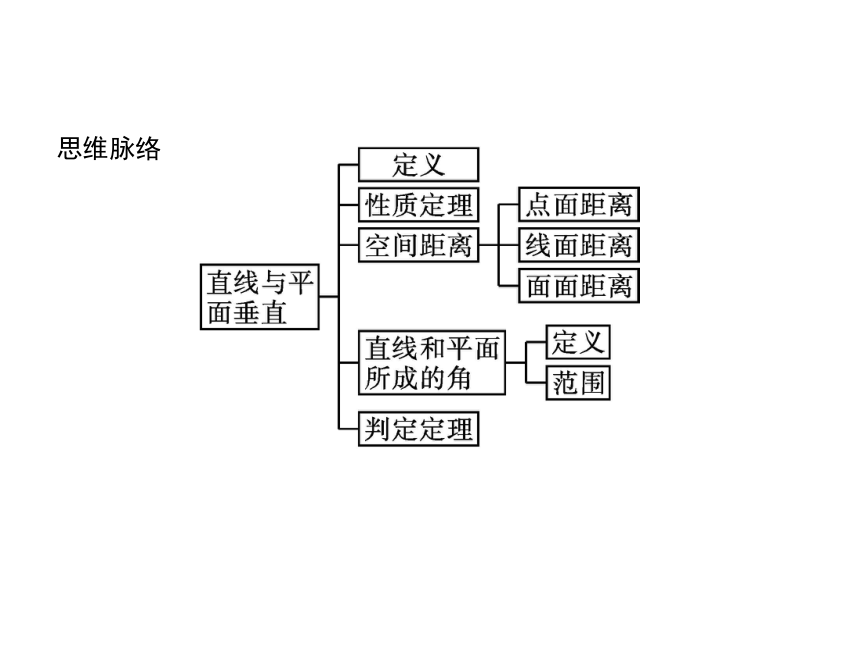
思维脉络
激趣诱思
知识点拨
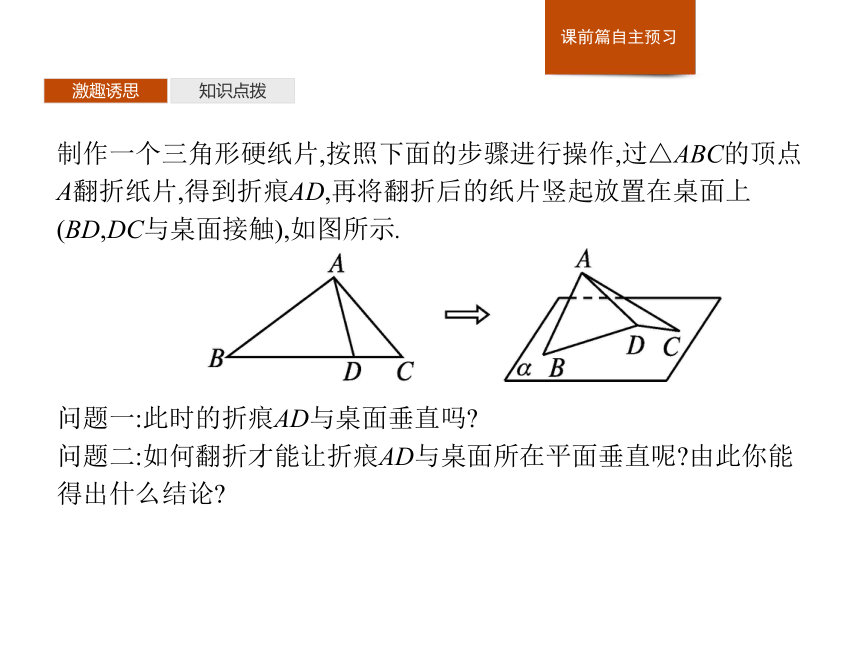
制作一个三角形硬纸片,按照下面的步骤进行操作,过△ABC的顶点A翻折纸片,得到折痕AD,再将翻折后的纸片竖起放置在桌面上(BD,DC与桌面接触),如图所示.
问题一:此时的折痕AD与桌面垂直吗?
问题二:如何翻折才能让折痕AD与桌面所在平面垂直呢?由此你能得出什么结论?
激趣诱思
知识点拨
一、直线与平面垂直
定义
如果直线l与平面α内的任意一条直线都垂直,那么称直线l与平面α垂直
记法
l⊥α
有关概念
直线l称为平面α的垂线,平面α称为直线l的垂面,它们唯一的公共点P称为垂足
图示
?
画法
画直线与平面垂直时,通常把直线画成与表示平面的平行四边形的一边垂直
激趣诱思
知识点拨
名师点析过一点垂直于已知平面的直线有且只有一条,该点与垂足间的线段称为这个点到该平面的垂线段,垂线段的长度称为这个点到该平面的距离.
微思考
空间两条直线垂直一定相交吗?
提示不一定相交,空间两条直线垂直分为两种情况:一种是相交垂直,一种是异面垂直.
微练习
直线l与平面α内的无数条直线垂直,则( )
A.l和α相互平行 B.l和α相互垂直
C.l在平面α内 D.不能确定
答案D
文字语言
垂直于同一个平面的两条直线平行
符号语言
图形语言
?
激趣诱思
知识点拨
二、直线与平面垂直的性质
名师点析一条直线与一个平面平行时,这条直线上任意一点到这个平面的距离,叫作这条直线到这个平面的距离,如果两个平面平行,那么其中一个平面内的任意一点到另一个平面的距离都相等,我们把它叫作这两个平行平面间的距离.
激趣诱思
知识点拨
微思考
垂直于同一平面的两条垂线一定共面吗?
提示共面,由线面垂直的性质定理可知这两条直线是平行的,故能确定一个平面.
微练习
在正方体ABCD-A1B1C1D1中,若直线l(与直线BB1不重合)⊥平面A1C1,则( )
A.B1B⊥l B.B1B∥l
C.B1B与l异面但不垂直 D.B1B与l相交但不垂直
解析因为B1B⊥平面A1C1,又因为l⊥平面A1C1,所以l∥B1B.
答案B
激趣诱思
知识点拨
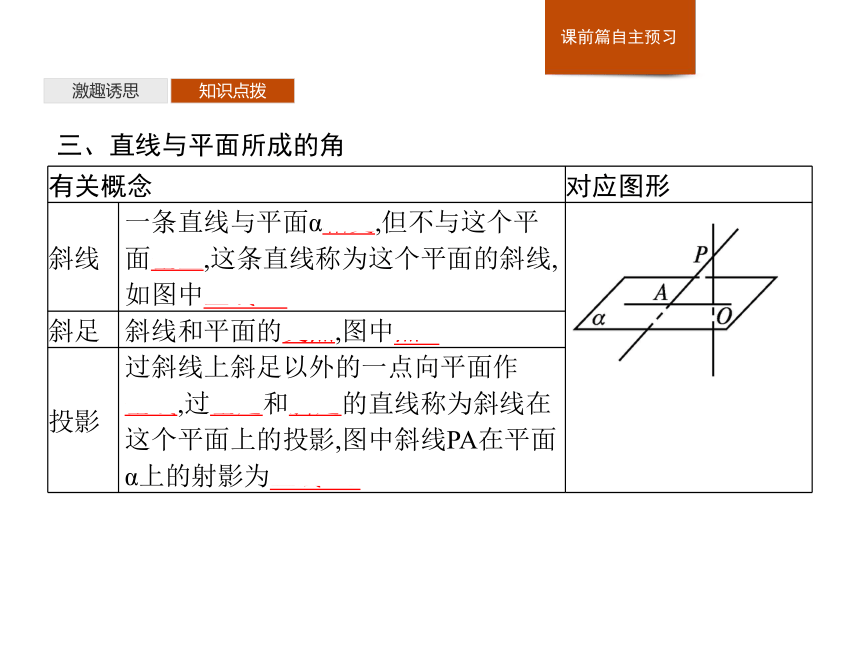
三、直线与平面所成的角
有关概念
对应图形
斜线
一条直线与平面α相交,但不与这个平面垂直,这条直线称为这个平面的斜线,如图中直线PA
?
斜足
斜线和平面的交点,图中点A
投影
过斜线上斜足以外的一点向平面作
垂线,过垂足和斜足的直线称为斜线在这个平面上的投影,图中斜线PA在平面α上的射影为直线AO
激趣诱思
知识点拨
直线与
平面所
成的角
定义:平面的一条斜线与它在平面上的投影所成的锐角,图中∠PAO
规定:一条直线垂直于平面,它们所成的角是直角;一条直线与平面平行,或在平面内,它们所成的角是0°的角
名师点析1.直线与平面所成的角是通过线线角来刻画的.
2.直线(斜线)与平面内的直线所成的角是不唯一的,而斜线与它在平面上的投影所成的角是唯一的,也是斜线与平面内的直线所成角中最小的一个.
激趣诱思
知识点拨
微思考
直线与平面所成的角θ的取值范围是什么?
提示一条直线垂直于平面,我们说它们所成的角等于90°;一条直线和平面平行,或在平面内,我们说它们所成的角等于0°.因此,直线与平面所成的角θ的范围是0°≤θ≤90°.
激趣诱思
知识点拨
微练习
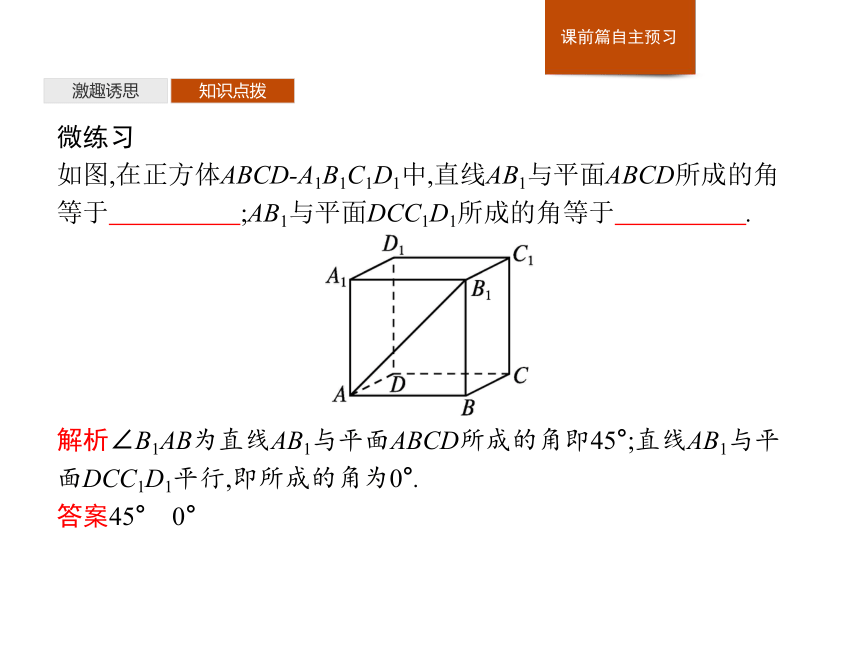
如图,在正方体ABCD-A1B1C1D1中,直线AB1与平面ABCD所成的角等于 ;AB1与平面DCC1D1所成的角等于 .?
解析∠B1AB为直线AB1与平面ABCD所成的角即45°;直线AB1与平面DCC1D1平行,即所成的角为0°.
答案45° 0°
激趣诱思
知识点拨
四、直线与平面垂直的判定
文字语言
如果一条直线与一个平面内的两条相交直线垂直,那么该直线与此平面垂直
符号语言
l⊥a,l⊥b,a?α,b?α,a∩b=P?l⊥α
图形语言
?
激趣诱思
知识点拨
名师点析 理解线面垂直的判定定理注意以下几点
(1)定理可表述为“线线垂直,则线面垂直”.
(2)“两条相交直线”是关键词,一定不要忽视这个条件,否则将导致结论错误,即“线不在多,相交就行”.
(3)要证明一条直线与一个平面垂直,只需在平面内找到两条相交直线和该直线垂直即可,至于这两条相交直线是否和已知直线有公共点无关紧要.
(4)线面垂直的判定定理与线面垂直的定义往往在证题过程中要反复交替使用.
激趣诱思
知识点拨
微思考
若把定理中的“两条相交直线”改为“两条直线”,直线与平面一定垂直吗?
提示当这两条直线平行时,直线可与平面平行或相交或在平面内,但不一定垂直.
激趣诱思
知识点拨
微判断
判断(正确的打“√”,错误的打“×”).
(1)如果一条直线垂直于平面内的无数条直线,那么这条直线和这个平面垂直.( )
(2)若直线垂直于平面内的两条直线,则这条直线与平面垂直.( )
(3)若直线垂直于梯形的两腰所在的直线,则这条直线垂直于两底边所在的直线.( )
(4)若直线垂直于梯形的两底边所在的直线,则这条直线垂直于两腰所在的直线.( )
答案(1)× (2)× (3)√ (4)×
激趣诱思
知识点拨
微练习
若三条直线OA,OB,OC两两垂直,则直线OA垂直于( )
A.平面OAB B.平面OAC
C.平面OBC D.平面ABC
答案C
探究一
探究二
探究三
探究四
当堂检测
证明直线与平面垂直
例1如图所示,AB⊥BC,△ABC所在平面外有一点S,且SA=SB=SC,AC中点为D.求证:SD⊥平面ABC.
证明因为SA=SC,D为AC中点,
所以SD⊥AC.
在Rt△ABC中,AD=DC=BD,
又SA=SB,所以△SDA≌△SDB.
所以∠SDA=∠SDB,即SD⊥DB.
又AC∩BD=D,所以SD⊥平面ABC.
探究一
探究二
探究三
探究四
当堂检测
反思感悟 判定直线与平面垂直,可以用定义,就是证明这条直线与平面内的任一直线垂直,但这种方法一般不用.最常用也最好用的是直线与平面垂直的判定定理,根据定理,只需证明这条直线与平面内的两条相交直线垂直即可.
另外,判定直线与平面垂直还有如下两个结论可用:
(1)两条平行直线中的一条垂直于一个平面,则另一条也垂直于这个平面.
(2)若一条直线与两平行平面中的一个面垂直,则它与另一个平面也垂直.
探究一
探究二
探究三
探究四
当堂检测
延伸探究在本例条件下,若AB=BC,求证:BD⊥平面SAC.
证明因为BA=BC,D为AC中点,
所以BD⊥AC.
因为SD⊥平面ABC,BD?平面ABC,
所以BD⊥SD,
因为AC与SD都在平面SAC内且相交,
所以BD⊥平面SAC.
探究一
探究二
探究三
探究四
当堂检测
求直线与平面所成的角
例2如图,在正方体ABCD-A1B1C1D1中,A1B与平面AA1D1D所成的角为 .?
解析因为AB⊥平面AA1D1D,
所以∠AA1B就是A1B与平面AA1D1D所成的角,
在Rt△AA1B中,∠BAA1=90°,AB=AA1,
所以∠AA1B=45°,
所以A1B与平面AA1D1D所成的角是45°.
答案45°
探究一
探究二
探究三
探究四
当堂检测
反思感悟 求直线与平面所成角的方法
(1)寻找过斜线上一点与平面垂直的直线.
(2)连接垂足和斜足得到斜线在平面上的投影,斜线与其投影所成的锐角或直角即为所求的角.
(3)把该角归结在某个三角形中,通过解三角形,求出该角.
探究一
探究二
探究三
探究四
当堂检测
变式训练1如图所示,三棱锥P-ABC中,PA⊥平面ABC,PA=AB,则直线PB与平面ABC所成角的度数为 .?
解析因为PA⊥平面ABC,所以斜线PB在平面ABC上的投影为AB,所以∠PBA即为直线PB与平面ABC所成的角.在△PAB中,∠BAP=90°,PA=AB,所以∠PBA=45°,即直线PB与平面ABC所成的角等于45°.
答案45°
探究一
探究二
探究三
探究四
当堂检测
直线与平面垂直的性质的应用
例3如图,在四棱锥P-ABCD中,底面ABCD是矩形,AB⊥平面PAD,AD=AP,E是PD的中点,M,N分别在AB,PC上,且MN⊥AB,MN⊥PC.证明:AE∥MN.
探究一
探究二
探究三
探究四
当堂检测
证明因为AB⊥平面PAD,AE?平面PAD,
所以AE⊥AB.
又AB∥CD,所以AE⊥CD.
因为AD=AP,E是PD的中点,所以AE⊥PD.
又CD∩PD=D,CD?平面PCD,PD?平面PCD,
所以AE⊥平面PCD.
因为MN⊥AB,AB∥CD,
所以MN⊥CD.
又因为MN⊥PC,PC∩CD=C,PC?平面PCD,CD?平面PCD,所以MN⊥平面PCD,
所以AE∥MN.
探究一
探究二
探究三
探究四
当堂检测
反思感悟 证明线线平行的常用方法
(1)利用线线平行定义:证共面且无公共点.
(2)利用基本事实4:证两线同时平行于第三条直线.
(3)利用线面平行的性质定理:把证线线平行转化为证线面平行.
(4)利用线面垂直的性质定理:把证线线平行转化为证线面垂直.
(5)利用面面平行的性质定理:把证线线平行转化为证面面平行.
探究一
探究二
探究三
探究四
当堂检测
变式训练2如图,α∩β=l,PA⊥α,PB⊥β,垂足分别为A,B,a?α,a⊥AB.求证:a∥l.
证明因为PA⊥α,l?α,所以PA⊥l.同理PB⊥l.
因为PA∩PB=P,PA?平面PAB,PB?平面PAB,
所以l⊥平面PAB.
又因为PA⊥α,a?α,所以PA⊥a.
因为a⊥AB,PA∩AB=A,PA?平面PAB,AB?平面PAB,
所以a⊥平面PAB.所以a∥l.
探究一
探究二
探究三
探究四
当堂检测
距离问题
例4如图所示,已知P为△ABC外一点,PA,PB,PC两两垂直,且PA=PB=PC=a,求点P到平面ABC的距离.
解过点P作PO⊥平面ABC于点O,连接AO,BO,CO,所以PO⊥OA,PO⊥OB,PO⊥OC.
因为PA=PB=PC=a,所以△PAO≌△PBO≌△PCO.
所以OA=OB=OC,所以O为△ABC的外心.
因为PA,PB,PC两两垂直,所以AB=BC=CA= a.
探究一
探究二
探究三
探究四
当堂检测
反思感悟 求点到平面距离的基本步骤
(1)找到或作出要求的距离;
(2)使所求距离在某一个三角形中;
(3)在三角形中根据三角形的边角关系求出距离.
探究一
探究二
探究三
探究四
当堂检测
变式训练3(2019全国Ⅰ高考)已知∠ACB=90°,P为平面ABC外一点,PC=2,点P到∠ACB两边AC,BC的距离均为 ,那么P到平面ABC的距离为 .?
探究一
探究二
探究三
探究四
当堂检测
解析作PD,PE分别垂直于AC,BC,PO⊥平面ABC.连接CO,OD,知CD⊥PD,CD⊥PO,PD∩PO=P,
所以CD⊥平面PDO,OD?平面PDO,
所以CD⊥OD.
探究一
探究二
探究三
探究四
当堂检测
1.(多选)在空间中,下列哪些命题是正确的( )
A.平行于同一条直线的两条直线互相平行
B.垂直于同一条直线的两条直线互相平行
C.平行于同一个平面的两条直线互相平行
D.垂直于同一个平面的两条直线互相平行
答案AD
探究一
探究二
探究三
探究四
当堂检测
2.如图,在正方体ABCD-A1B1C1D1中,与AD1垂直的平面是( )
A.平面DD1C1C
B.平面A1DB1
C.平面A1B1C1D1
D.平面A1DB
解析因为AD1⊥A1D,AD1⊥A1B1,A1D∩A1B1=A1,A1D?平面A1DB1,A1B1?平面A1DB1,所以AD1⊥平面A1DB1.
答案B
探究一
探究二
探究三
探究四
当堂检测
3.在长方体ABCD-A1B1C1D1中,AB= ,BC=AA1=1,则BD1与平面A1B1C1D1所成的角的大小为 .?
解析如图所示,连接B1D1,
则B1D1是BD1在平面A1B1C1D1上的投影,
则∠BD1B1是BD1与平面A1B1C1D1所成的角.
则∠BD1B1=30°.
答案30°
探究一
探究二
探究三
探究四
当堂检测
4.如图所示,在正方体ABCD-A1B1C1D1中,EF与异面直线AC,A1D都垂直相交.求证:EF∥BD1.
探究一
探究二
探究三
探究四
当堂检测
证明如图,连接AB1,B1C,BD,B1D1.
因为DD1⊥平面ABCD,AC?平面ABCD,
所以DD1⊥AC.
又AC⊥BD,DD1∩BD=D,
所以AC⊥平面BDD1B1,所以AC⊥BD1.
同理,BD1⊥B1C,且AC∩B1C=C,
所以BD1⊥平面AB1C.
因为EF⊥A1D,且A1D∥B1C,所以EF⊥B1C.
又因为EF⊥AC,B1C∩AC=C,
所以EF⊥平面AB1C,所以EF∥BD1.
课标阐释
1.借助常见几何体了解直线与平面垂直的定义,了解直线与平面所成角的概念.(数学抽象,几何直观)
2.掌握直线与平面垂直的性质定理,并会用定理证明相关问题.(逻辑推理)
3.掌握直线与平面垂直的判定定理,并会用定理判定线面垂直.(逻辑推理)
4.会求简单的空间距离问题(点面距离、线面距离、面面距离).(数学运算)
思维脉络
激趣诱思
知识点拨
制作一个三角形硬纸片,按照下面的步骤进行操作,过△ABC的顶点A翻折纸片,得到折痕AD,再将翻折后的纸片竖起放置在桌面上(BD,DC与桌面接触),如图所示.
问题一:此时的折痕AD与桌面垂直吗?
问题二:如何翻折才能让折痕AD与桌面所在平面垂直呢?由此你能得出什么结论?
激趣诱思
知识点拨
一、直线与平面垂直
定义
如果直线l与平面α内的任意一条直线都垂直,那么称直线l与平面α垂直
记法
l⊥α
有关概念
直线l称为平面α的垂线,平面α称为直线l的垂面,它们唯一的公共点P称为垂足
图示
?
画法
画直线与平面垂直时,通常把直线画成与表示平面的平行四边形的一边垂直
激趣诱思
知识点拨
名师点析过一点垂直于已知平面的直线有且只有一条,该点与垂足间的线段称为这个点到该平面的垂线段,垂线段的长度称为这个点到该平面的距离.
微思考
空间两条直线垂直一定相交吗?
提示不一定相交,空间两条直线垂直分为两种情况:一种是相交垂直,一种是异面垂直.
微练习
直线l与平面α内的无数条直线垂直,则( )
A.l和α相互平行 B.l和α相互垂直
C.l在平面α内 D.不能确定
答案D
文字语言
垂直于同一个平面的两条直线平行
符号语言
图形语言
?
激趣诱思
知识点拨
二、直线与平面垂直的性质
名师点析一条直线与一个平面平行时,这条直线上任意一点到这个平面的距离,叫作这条直线到这个平面的距离,如果两个平面平行,那么其中一个平面内的任意一点到另一个平面的距离都相等,我们把它叫作这两个平行平面间的距离.
激趣诱思
知识点拨
微思考
垂直于同一平面的两条垂线一定共面吗?
提示共面,由线面垂直的性质定理可知这两条直线是平行的,故能确定一个平面.
微练习
在正方体ABCD-A1B1C1D1中,若直线l(与直线BB1不重合)⊥平面A1C1,则( )
A.B1B⊥l B.B1B∥l
C.B1B与l异面但不垂直 D.B1B与l相交但不垂直
解析因为B1B⊥平面A1C1,又因为l⊥平面A1C1,所以l∥B1B.
答案B
激趣诱思
知识点拨
三、直线与平面所成的角
有关概念
对应图形
斜线
一条直线与平面α相交,但不与这个平面垂直,这条直线称为这个平面的斜线,如图中直线PA
?
斜足
斜线和平面的交点,图中点A
投影
过斜线上斜足以外的一点向平面作
垂线,过垂足和斜足的直线称为斜线在这个平面上的投影,图中斜线PA在平面α上的射影为直线AO
激趣诱思
知识点拨
直线与
平面所
成的角
定义:平面的一条斜线与它在平面上的投影所成的锐角,图中∠PAO
规定:一条直线垂直于平面,它们所成的角是直角;一条直线与平面平行,或在平面内,它们所成的角是0°的角
名师点析1.直线与平面所成的角是通过线线角来刻画的.
2.直线(斜线)与平面内的直线所成的角是不唯一的,而斜线与它在平面上的投影所成的角是唯一的,也是斜线与平面内的直线所成角中最小的一个.
激趣诱思
知识点拨
微思考
直线与平面所成的角θ的取值范围是什么?
提示一条直线垂直于平面,我们说它们所成的角等于90°;一条直线和平面平行,或在平面内,我们说它们所成的角等于0°.因此,直线与平面所成的角θ的范围是0°≤θ≤90°.
激趣诱思
知识点拨
微练习
如图,在正方体ABCD-A1B1C1D1中,直线AB1与平面ABCD所成的角等于 ;AB1与平面DCC1D1所成的角等于 .?
解析∠B1AB为直线AB1与平面ABCD所成的角即45°;直线AB1与平面DCC1D1平行,即所成的角为0°.
答案45° 0°
激趣诱思
知识点拨
四、直线与平面垂直的判定
文字语言
如果一条直线与一个平面内的两条相交直线垂直,那么该直线与此平面垂直
符号语言
l⊥a,l⊥b,a?α,b?α,a∩b=P?l⊥α
图形语言
?
激趣诱思
知识点拨
名师点析 理解线面垂直的判定定理注意以下几点
(1)定理可表述为“线线垂直,则线面垂直”.
(2)“两条相交直线”是关键词,一定不要忽视这个条件,否则将导致结论错误,即“线不在多,相交就行”.
(3)要证明一条直线与一个平面垂直,只需在平面内找到两条相交直线和该直线垂直即可,至于这两条相交直线是否和已知直线有公共点无关紧要.
(4)线面垂直的判定定理与线面垂直的定义往往在证题过程中要反复交替使用.
激趣诱思
知识点拨
微思考
若把定理中的“两条相交直线”改为“两条直线”,直线与平面一定垂直吗?
提示当这两条直线平行时,直线可与平面平行或相交或在平面内,但不一定垂直.
激趣诱思
知识点拨
微判断
判断(正确的打“√”,错误的打“×”).
(1)如果一条直线垂直于平面内的无数条直线,那么这条直线和这个平面垂直.( )
(2)若直线垂直于平面内的两条直线,则这条直线与平面垂直.( )
(3)若直线垂直于梯形的两腰所在的直线,则这条直线垂直于两底边所在的直线.( )
(4)若直线垂直于梯形的两底边所在的直线,则这条直线垂直于两腰所在的直线.( )
答案(1)× (2)× (3)√ (4)×
激趣诱思
知识点拨
微练习
若三条直线OA,OB,OC两两垂直,则直线OA垂直于( )
A.平面OAB B.平面OAC
C.平面OBC D.平面ABC
答案C
探究一
探究二
探究三
探究四
当堂检测
证明直线与平面垂直
例1如图所示,AB⊥BC,△ABC所在平面外有一点S,且SA=SB=SC,AC中点为D.求证:SD⊥平面ABC.
证明因为SA=SC,D为AC中点,
所以SD⊥AC.
在Rt△ABC中,AD=DC=BD,
又SA=SB,所以△SDA≌△SDB.
所以∠SDA=∠SDB,即SD⊥DB.
又AC∩BD=D,所以SD⊥平面ABC.
探究一
探究二
探究三
探究四
当堂检测
反思感悟 判定直线与平面垂直,可以用定义,就是证明这条直线与平面内的任一直线垂直,但这种方法一般不用.最常用也最好用的是直线与平面垂直的判定定理,根据定理,只需证明这条直线与平面内的两条相交直线垂直即可.
另外,判定直线与平面垂直还有如下两个结论可用:
(1)两条平行直线中的一条垂直于一个平面,则另一条也垂直于这个平面.
(2)若一条直线与两平行平面中的一个面垂直,则它与另一个平面也垂直.
探究一
探究二
探究三
探究四
当堂检测
延伸探究在本例条件下,若AB=BC,求证:BD⊥平面SAC.
证明因为BA=BC,D为AC中点,
所以BD⊥AC.
因为SD⊥平面ABC,BD?平面ABC,
所以BD⊥SD,
因为AC与SD都在平面SAC内且相交,
所以BD⊥平面SAC.
探究一
探究二
探究三
探究四
当堂检测
求直线与平面所成的角
例2如图,在正方体ABCD-A1B1C1D1中,A1B与平面AA1D1D所成的角为 .?
解析因为AB⊥平面AA1D1D,
所以∠AA1B就是A1B与平面AA1D1D所成的角,
在Rt△AA1B中,∠BAA1=90°,AB=AA1,
所以∠AA1B=45°,
所以A1B与平面AA1D1D所成的角是45°.
答案45°
探究一
探究二
探究三
探究四
当堂检测
反思感悟 求直线与平面所成角的方法
(1)寻找过斜线上一点与平面垂直的直线.
(2)连接垂足和斜足得到斜线在平面上的投影,斜线与其投影所成的锐角或直角即为所求的角.
(3)把该角归结在某个三角形中,通过解三角形,求出该角.
探究一
探究二
探究三
探究四
当堂检测
变式训练1如图所示,三棱锥P-ABC中,PA⊥平面ABC,PA=AB,则直线PB与平面ABC所成角的度数为 .?
解析因为PA⊥平面ABC,所以斜线PB在平面ABC上的投影为AB,所以∠PBA即为直线PB与平面ABC所成的角.在△PAB中,∠BAP=90°,PA=AB,所以∠PBA=45°,即直线PB与平面ABC所成的角等于45°.
答案45°
探究一
探究二
探究三
探究四
当堂检测
直线与平面垂直的性质的应用
例3如图,在四棱锥P-ABCD中,底面ABCD是矩形,AB⊥平面PAD,AD=AP,E是PD的中点,M,N分别在AB,PC上,且MN⊥AB,MN⊥PC.证明:AE∥MN.
探究一
探究二
探究三
探究四
当堂检测
证明因为AB⊥平面PAD,AE?平面PAD,
所以AE⊥AB.
又AB∥CD,所以AE⊥CD.
因为AD=AP,E是PD的中点,所以AE⊥PD.
又CD∩PD=D,CD?平面PCD,PD?平面PCD,
所以AE⊥平面PCD.
因为MN⊥AB,AB∥CD,
所以MN⊥CD.
又因为MN⊥PC,PC∩CD=C,PC?平面PCD,CD?平面PCD,所以MN⊥平面PCD,
所以AE∥MN.
探究一
探究二
探究三
探究四
当堂检测
反思感悟 证明线线平行的常用方法
(1)利用线线平行定义:证共面且无公共点.
(2)利用基本事实4:证两线同时平行于第三条直线.
(3)利用线面平行的性质定理:把证线线平行转化为证线面平行.
(4)利用线面垂直的性质定理:把证线线平行转化为证线面垂直.
(5)利用面面平行的性质定理:把证线线平行转化为证面面平行.
探究一
探究二
探究三
探究四
当堂检测
变式训练2如图,α∩β=l,PA⊥α,PB⊥β,垂足分别为A,B,a?α,a⊥AB.求证:a∥l.
证明因为PA⊥α,l?α,所以PA⊥l.同理PB⊥l.
因为PA∩PB=P,PA?平面PAB,PB?平面PAB,
所以l⊥平面PAB.
又因为PA⊥α,a?α,所以PA⊥a.
因为a⊥AB,PA∩AB=A,PA?平面PAB,AB?平面PAB,
所以a⊥平面PAB.所以a∥l.
探究一
探究二
探究三
探究四
当堂检测
距离问题
例4如图所示,已知P为△ABC外一点,PA,PB,PC两两垂直,且PA=PB=PC=a,求点P到平面ABC的距离.
解过点P作PO⊥平面ABC于点O,连接AO,BO,CO,所以PO⊥OA,PO⊥OB,PO⊥OC.
因为PA=PB=PC=a,所以△PAO≌△PBO≌△PCO.
所以OA=OB=OC,所以O为△ABC的外心.
因为PA,PB,PC两两垂直,所以AB=BC=CA= a.
探究一
探究二
探究三
探究四
当堂检测
反思感悟 求点到平面距离的基本步骤
(1)找到或作出要求的距离;
(2)使所求距离在某一个三角形中;
(3)在三角形中根据三角形的边角关系求出距离.
探究一
探究二
探究三
探究四
当堂检测
变式训练3(2019全国Ⅰ高考)已知∠ACB=90°,P为平面ABC外一点,PC=2,点P到∠ACB两边AC,BC的距离均为 ,那么P到平面ABC的距离为 .?
探究一
探究二
探究三
探究四
当堂检测
解析作PD,PE分别垂直于AC,BC,PO⊥平面ABC.连接CO,OD,知CD⊥PD,CD⊥PO,PD∩PO=P,
所以CD⊥平面PDO,OD?平面PDO,
所以CD⊥OD.
探究一
探究二
探究三
探究四
当堂检测
1.(多选)在空间中,下列哪些命题是正确的( )
A.平行于同一条直线的两条直线互相平行
B.垂直于同一条直线的两条直线互相平行
C.平行于同一个平面的两条直线互相平行
D.垂直于同一个平面的两条直线互相平行
答案AD
探究一
探究二
探究三
探究四
当堂检测
2.如图,在正方体ABCD-A1B1C1D1中,与AD1垂直的平面是( )
A.平面DD1C1C
B.平面A1DB1
C.平面A1B1C1D1
D.平面A1DB
解析因为AD1⊥A1D,AD1⊥A1B1,A1D∩A1B1=A1,A1D?平面A1DB1,A1B1?平面A1DB1,所以AD1⊥平面A1DB1.
答案B
探究一
探究二
探究三
探究四
当堂检测
3.在长方体ABCD-A1B1C1D1中,AB= ,BC=AA1=1,则BD1与平面A1B1C1D1所成的角的大小为 .?
解析如图所示,连接B1D1,
则B1D1是BD1在平面A1B1C1D1上的投影,
则∠BD1B1是BD1与平面A1B1C1D1所成的角.
则∠BD1B1=30°.
答案30°
探究一
探究二
探究三
探究四
当堂检测
4.如图所示,在正方体ABCD-A1B1C1D1中,EF与异面直线AC,A1D都垂直相交.求证:EF∥BD1.
探究一
探究二
探究三
探究四
当堂检测
证明如图,连接AB1,B1C,BD,B1D1.
因为DD1⊥平面ABCD,AC?平面ABCD,
所以DD1⊥AC.
又AC⊥BD,DD1∩BD=D,
所以AC⊥平面BDD1B1,所以AC⊥BD1.
同理,BD1⊥B1C,且AC∩B1C=C,
所以BD1⊥平面AB1C.
因为EF⊥A1D,且A1D∥B1C,所以EF⊥B1C.
又因为EF⊥AC,B1C∩AC=C,
所以EF⊥平面AB1C,所以EF∥BD1.
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
