高一数学人教B版(2019)必修第一册3.1.1函数及其表示方法(1)-课件24张PPT
文档属性
| 名称 | 高一数学人教B版(2019)必修第一册3.1.1函数及其表示方法(1)-课件24张PPT |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-20 00:00:00 | ||
图片预览







文档简介
函数及其表示方法(1)
高一年级 数学
一、复习初中函数概念:
在一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么就称y是x的函数.
初中学过很多函数都可以用一个解析式表示,如正比例函数y=2x,二次函数y=x?+2x-3等.
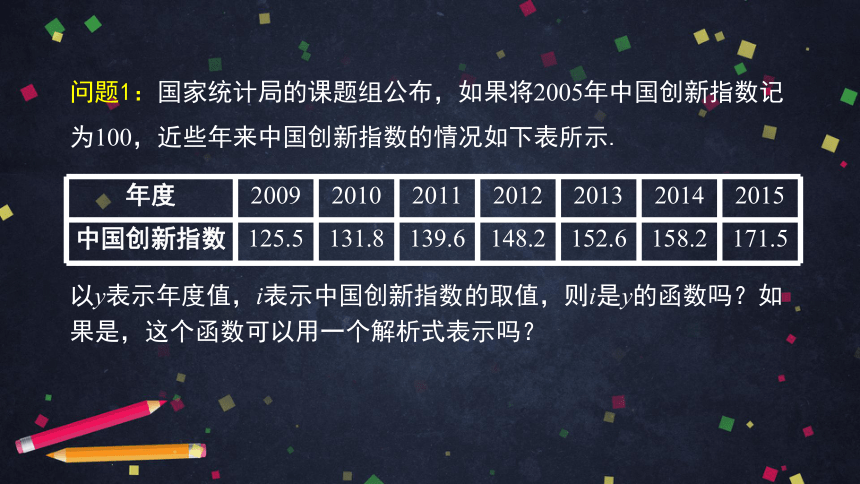
问题1:国家统计局的课题组公布,如果将2005年中国创新指数记为100,近些年来中国创新指数的情况如下表所示.
以y表示年度值,i表示中国创新指数的取值,则i是y的函数吗?如果是,这个函数可以用一个解析式表示吗?
{2D5ABB26-0587-4C30-8999-92F81FD0307C}年度
2009
2010
2011
2012
2013
2014
2015
中国创新指数
125.5
131.8
139.6
148.2
152.6
158.2
171.5
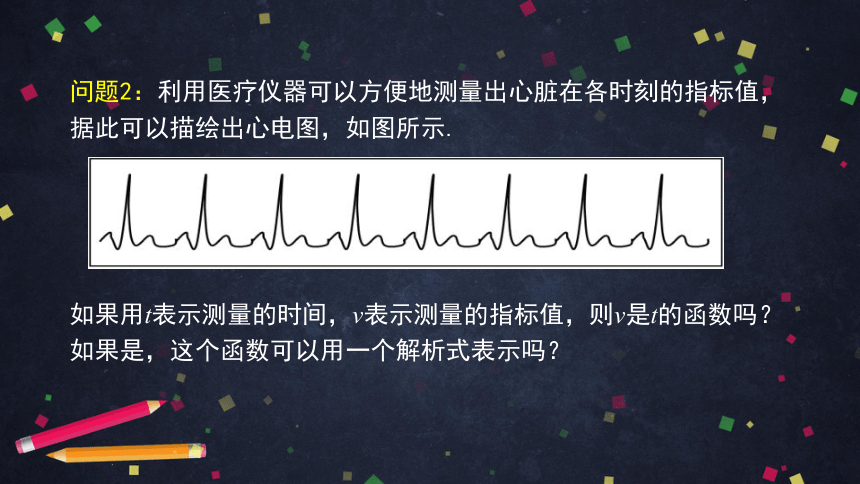
问题2:利用医疗仪器可以方便地测量出心脏在各时刻的指标值,据此可以描绘出心电图,如图所示.
如果用t表示测量的时间,v表示测量的指标值,则v是t的函数吗?如果是,这个函数可以用一个解析式表示吗?
一般地,给定两个非空实数集A与B,以及对应关系f,如果对于集合A中的每一个实数x,在集合B中都有唯一确定的实数y与x对应,则称f为定义在集合A上的一个函数.
二、函数概念:
其中对应关系f具有不同的数学形式,有的是一个解析式,有的是一个表格,有的是一个图像.
x称为自变量,y称为因变量,自变量取值的范围(即数集A)称为这个函数的定义域.
与x对应的函数值记作f(x),即y=f(x). 如y=x?中,x=2时,y=4,可记为f(2)=4. 所有函数值组成的集合
称为函数的值域.
由此对应关系确定的函数记作
函数的对应关系一般用小写英文字母f,g,h…表示,有时也可用大写英文字母F,G,H,…表示.
如:正比例函数y=2x,若记其对应关系为f,则f是定义在A=R上的一个函数,此函数可记为f(x)=2x,f(0)表示与x=0对应的函数值,即f(0)=2×0=0; f(3)表示与3对应的函数值,即f(3)= ;
函数f(x)=2x的定义域为 ,值域为 ;
6
R
R
{2D5ABB26-0587-4C30-8999-92F81FD0307C}年度
2009
2010
2011
2012
2013
2014
2015
中国创新指数
125.5
131.8
139.6
148.2
152.6
158.2
171.5
问题1中,若记其对应关系为g,则g是定义在A={2009,…,2015}上的一个函数,此函数函数可记为i=g(y),g(2009)= ,g(2012)= ;
其定义域为 ,
值域为 .
125.5
148.2
{125.5, 131.8, 139.6, 148.2, 152.6, 158.2, 171.5}
{2009, 2010, 2011, 2012, 2013, 2014, 2015}
说明:
⑴在此定义下,函数就有了统一的、一般的符号表示,如正比例函数可记为y=f(x)=2x,问题1中的函数可记为i=g(y),问题2中的函数可记为v=h(t);
⑵在函数的这种表示中,自变量、因变量以及对应关系用什么字母来表示是无关紧要的,例如函数f(x)=2x+1,x?R与g(s)=2s+1,s?R应该看成同一个函数. 习惯上,人们总是用x表示自变量,y表示因变量.
三、思考判断:
1.分别判断 f 是否为A上的一个函数(函数值均为R中的元素):
⑴ A=R,f 为“加1”;
⑵ A=[0,+∞),f 为“求平方根”;
⑶ A=R,f 为“求倒数”.
(是)
(不是)
(不是)
总结:f 不是A上的函数的两种常见情形
⑴ ;
⑵ .
存在A中某元素在B中没有元素与之对应
存在A中某元素在B中有2个或2个以上的元素与之对应
2.判断下列各组函数是否为同一个函数:
⑴
⑵
⑶
(不是,定义域不同)
(不是,对应关系不同)
(是)
总结:如果两个函数的 相同, 也相同(则____一定相同),那么这两个函数就是同一个函数.
定义域
对应关系
值域
说明:在表示函数时,如果不会产生歧义,函数的定义域通常省略不写,此时约定:函数的定义域就是使得这个函数有意义的所有实数组成的集合. 如函数f(x)=2x+1, 其定义域就是R.
四、例题选讲
例1.求下列函数的定义域:
⑴
解:因为函数有意义当且仅当
所以函数定义域为
⑵
解:因为函数有意义当且仅当
所以函数定义域为
总结:⑴求函数定义域常用依据,
① ;
② ;
③ .
⑵常见错误: .
分式中分母不能为零
二次根式中被开方数要大于或等于零
零次幂的底数不能为零
把函数化为 再求定义域
例2.已知函数 .
⑴求f(0), f(1), f(3)的值;
⑵当x∈[0,3]时,求f(x)的值域.
解:⑴由已知可得
例2.已知函数 .
⑴求f(0), f(1), f(3)的值;
⑵当x∈[0,3]时,求f(x)的值域.
解:⑵因为 ,其图像
为开口向上抛物线,且对称轴为x=1,
所以当x=1时,有最小值为2;
由⑴知,f(0) 所以当x=3时,有最大值为6.
综上所述,函数值域为[2,6].
总结:求函数值域的一种常用方法是画出函数图像,根据定义域观察截取函数图像,进而求得函数值域.
常见错误:把定义域两个端点直接代入计算!
五、课堂小结
1.你有哪些收获?
①知识: ;
②思想方法: ;
③经验: .
2.你还有什么困惑?
.
函数概念、符号、定义域、值域、对应关系等
抽象概括、数形结合等数学思想方法
函数值域不能只代入定义域端点值等
作业
人教社B版课本
P93练习A第1,2题
作业
P94练习B第5,6题
谢谢
高一年级 数学
一、复习初中函数概念:
在一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么就称y是x的函数.
初中学过很多函数都可以用一个解析式表示,如正比例函数y=2x,二次函数y=x?+2x-3等.
问题1:国家统计局的课题组公布,如果将2005年中国创新指数记为100,近些年来中国创新指数的情况如下表所示.
以y表示年度值,i表示中国创新指数的取值,则i是y的函数吗?如果是,这个函数可以用一个解析式表示吗?
{2D5ABB26-0587-4C30-8999-92F81FD0307C}年度
2009
2010
2011
2012
2013
2014
2015
中国创新指数
125.5
131.8
139.6
148.2
152.6
158.2
171.5
问题2:利用医疗仪器可以方便地测量出心脏在各时刻的指标值,据此可以描绘出心电图,如图所示.
如果用t表示测量的时间,v表示测量的指标值,则v是t的函数吗?如果是,这个函数可以用一个解析式表示吗?
一般地,给定两个非空实数集A与B,以及对应关系f,如果对于集合A中的每一个实数x,在集合B中都有唯一确定的实数y与x对应,则称f为定义在集合A上的一个函数.
二、函数概念:
其中对应关系f具有不同的数学形式,有的是一个解析式,有的是一个表格,有的是一个图像.
x称为自变量,y称为因变量,自变量取值的范围(即数集A)称为这个函数的定义域.
与x对应的函数值记作f(x),即y=f(x). 如y=x?中,x=2时,y=4,可记为f(2)=4. 所有函数值组成的集合
称为函数的值域.
由此对应关系确定的函数记作
函数的对应关系一般用小写英文字母f,g,h…表示,有时也可用大写英文字母F,G,H,…表示.
如:正比例函数y=2x,若记其对应关系为f,则f是定义在A=R上的一个函数,此函数可记为f(x)=2x,f(0)表示与x=0对应的函数值,即f(0)=2×0=0; f(3)表示与3对应的函数值,即f(3)= ;
函数f(x)=2x的定义域为 ,值域为 ;
6
R
R
{2D5ABB26-0587-4C30-8999-92F81FD0307C}年度
2009
2010
2011
2012
2013
2014
2015
中国创新指数
125.5
131.8
139.6
148.2
152.6
158.2
171.5
问题1中,若记其对应关系为g,则g是定义在A={2009,…,2015}上的一个函数,此函数函数可记为i=g(y),g(2009)= ,g(2012)= ;
其定义域为 ,
值域为 .
125.5
148.2
{125.5, 131.8, 139.6, 148.2, 152.6, 158.2, 171.5}
{2009, 2010, 2011, 2012, 2013, 2014, 2015}
说明:
⑴在此定义下,函数就有了统一的、一般的符号表示,如正比例函数可记为y=f(x)=2x,问题1中的函数可记为i=g(y),问题2中的函数可记为v=h(t);
⑵在函数的这种表示中,自变量、因变量以及对应关系用什么字母来表示是无关紧要的,例如函数f(x)=2x+1,x?R与g(s)=2s+1,s?R应该看成同一个函数. 习惯上,人们总是用x表示自变量,y表示因变量.
三、思考判断:
1.分别判断 f 是否为A上的一个函数(函数值均为R中的元素):
⑴ A=R,f 为“加1”;
⑵ A=[0,+∞),f 为“求平方根”;
⑶ A=R,f 为“求倒数”.
(是)
(不是)
(不是)
总结:f 不是A上的函数的两种常见情形
⑴ ;
⑵ .
存在A中某元素在B中没有元素与之对应
存在A中某元素在B中有2个或2个以上的元素与之对应
2.判断下列各组函数是否为同一个函数:
⑴
⑵
⑶
(不是,定义域不同)
(不是,对应关系不同)
(是)
总结:如果两个函数的 相同, 也相同(则____一定相同),那么这两个函数就是同一个函数.
定义域
对应关系
值域
说明:在表示函数时,如果不会产生歧义,函数的定义域通常省略不写,此时约定:函数的定义域就是使得这个函数有意义的所有实数组成的集合. 如函数f(x)=2x+1, 其定义域就是R.
四、例题选讲
例1.求下列函数的定义域:
⑴
解:因为函数有意义当且仅当
所以函数定义域为
⑵
解:因为函数有意义当且仅当
所以函数定义域为
总结:⑴求函数定义域常用依据,
① ;
② ;
③ .
⑵常见错误: .
分式中分母不能为零
二次根式中被开方数要大于或等于零
零次幂的底数不能为零
把函数化为 再求定义域
例2.已知函数 .
⑴求f(0), f(1), f(3)的值;
⑵当x∈[0,3]时,求f(x)的值域.
解:⑴由已知可得
例2.已知函数 .
⑴求f(0), f(1), f(3)的值;
⑵当x∈[0,3]时,求f(x)的值域.
解:⑵因为 ,其图像
为开口向上抛物线,且对称轴为x=1,
所以当x=1时,有最小值为2;
由⑴知,f(0)
综上所述,函数值域为[2,6].
总结:求函数值域的一种常用方法是画出函数图像,根据定义域观察截取函数图像,进而求得函数值域.
常见错误:把定义域两个端点直接代入计算!
五、课堂小结
1.你有哪些收获?
①知识: ;
②思想方法: ;
③经验: .
2.你还有什么困惑?
.
函数概念、符号、定义域、值域、对应关系等
抽象概括、数形结合等数学思想方法
函数值域不能只代入定义域端点值等
作业
人教社B版课本
P93练习A第1,2题
作业
P94练习B第5,6题
谢谢
