高中数学人教A版必修二:4.2.3 直线与圆的方程的应用 课件20张PPT
文档属性
| 名称 | 高中数学人教A版必修二:4.2.3 直线与圆的方程的应用 课件20张PPT |

|
|
| 格式 | ppt | ||
| 文件大小 | 183.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-20 19:04:18 | ||
图片预览






文档简介
4.2.3《直线与圆
的方程的应用》
学习目标:
1.理解直线与圆的位置关系的几何性质;
2.利用平面直角坐标系解决直线与圆的位置关系;
3.会用“数形结合”的数学思想解决问题.
复习:
(1)直线方程有几种形式?分别为什么?
(2)圆的方程有几种形式?分别是哪些?
(3)求圆的方程时,什么条件下,用标准方程?什么条件下用一般方程?
(4)如何用直线和圆的方程判断它们之间的位置关系?
(5)如何根据圆的方程,判断它们之间的位置关系?
求直线l:2x-y-2=0被圆C:(x-3)?+y?=9所截得的弦长。
前提测试:
知识探究:直线与圆的方程在实际生活中的应用
问题Ⅰ:一艘轮船在沿直线返回港口的途中,接到气象台的台风预报:台风中心位于轮船正西70 km处, 受影响的范围是半径长为30km的圆形区域. 已知港口位于台风中心正北40 km处,如果这艘轮船不改变航线,那么它是否会受到台风的影响?
轮船
港口
台风
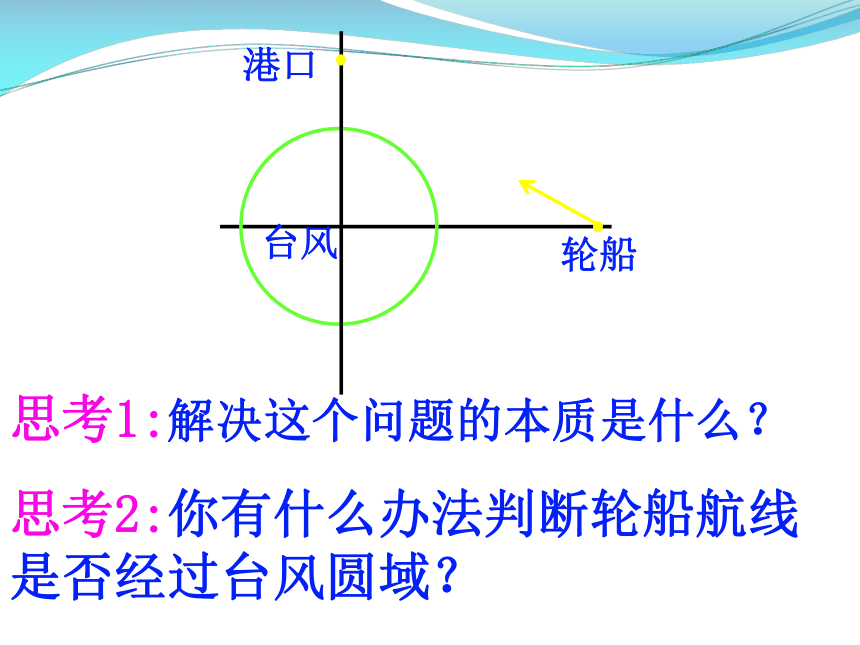
思考1:解决这个问题的本质是什么?
思考2:你有什么办法判断轮船航线是否经过台风圆域?
轮船
港口
台风
x
y
o
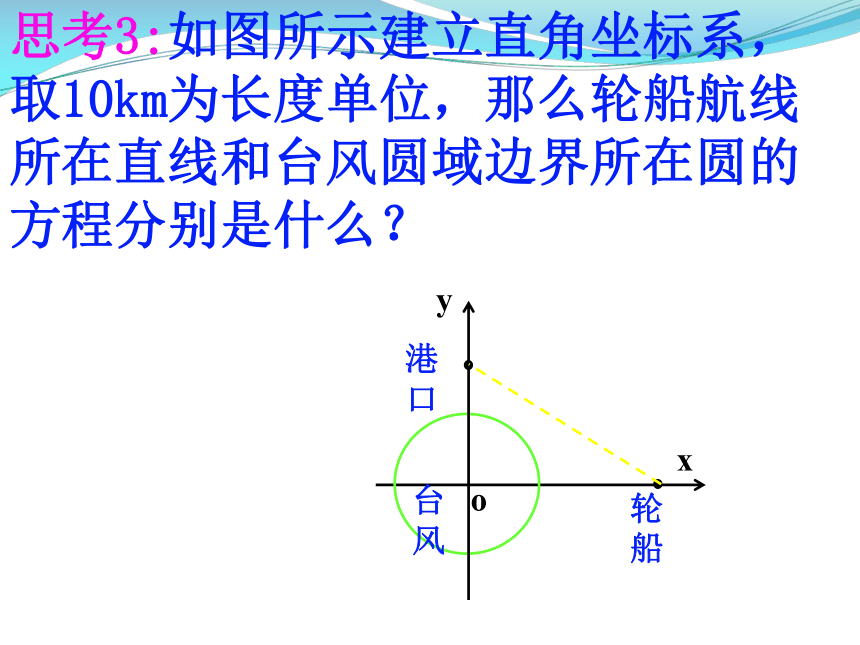
思考3:如图所示建立直角坐标系,取10km为长度单位,那么轮船航线所在直线和台风圆域边界所在圆的方程分别是什么?
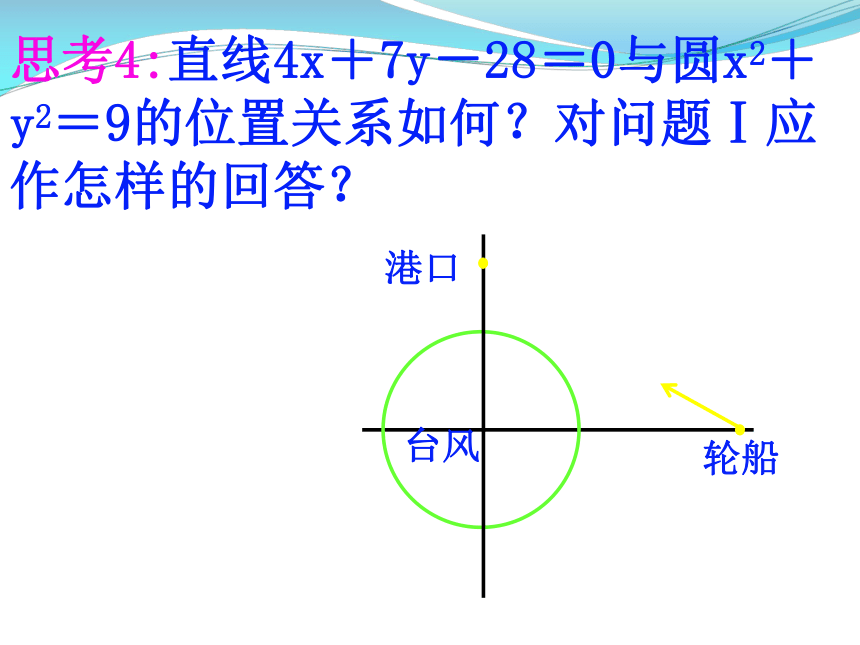
思考4:直线4x+7y-28=0与圆x2+y2=9的位置关系如何?对问题Ⅰ应作怎样的回答?
轮船
港口
台风
第一步:建立适当的平面直角坐标系,用坐标和方程表示问题中的几何元素,将平面几何问题转化为代数问题;
第二步:通过代数运算,解决代数问题;
第三步:将代数运算结果“翻译”成几何结论.
问题Ⅱ:如图是某圆拱形桥一孔圆拱的示意图. 这个圆的圆拱跨度AB=20m,拱高OP=4m,建造时每间隔4m需要用一根支柱支撑,求支柱A2P2的高度(精确到0.01m)
A
B
A1
A2
A3
A4
O
P
P2
思考1:你能用几何法求支柱A2P2的高度吗?
思考2:如图所示建立直角坐标系,那么求支柱A2P2的高度,化归为求一个什么问题?
A
B
A1
A2
A3
A4
O
P
P2
x
y
思考4:利用这个圆的方程可求得点P2的纵坐标是多少?问题Ⅱ的答案如何?
思考3:取1m为长度单位,如何求圆拱所在圆的方程?
x2+(y+10.5)2=14.52
A
B
A1
A2
A3
A4
O
P
P2
x
y
巩固练习:
某圆拱桥的水面跨度20m,拱高4m,现有一船,宽10m,水面以上高3m,这条船能否从桥下通过?
知识探究:直线与圆的方程在平面几何中的应用
问题Ⅲ:已知内接于圆的四边形的对角线互相垂直,求证:圆心到一边的距离等于这条边所对边长的一半.
思考1:许多平面几何问题常利用“坐标法”来解决,首先要做的工作是建立适当的直角坐标系,在本题中应如何选取坐标系?
X
y
o
思考2:如图所示建立直角坐标系,设四边形的四个顶点分别为点 A(a,0),B(0,b),C(c,0), D(0,d),那么BC边的长为多少?
A
B
C
D
M
x
y
o
N
思考3:四边形ABCD的外接圆圆心M的坐标如何?
思考4:如何计算圆心M到直线AD的距离|MN|?
A
B
C
D
M
x
y
o
N
课堂小结:
第一步:建立适当的平面直角坐标系,用坐标和方程表示问题中的几何元素,将平面几何问题转化为代数问题;
第二步:通过代数运算,解决代数问题;
第三步:将代数运算结果“翻译”成几何结论.
作业:
课本133页第7,8,9,10题
再见!
的方程的应用》
学习目标:
1.理解直线与圆的位置关系的几何性质;
2.利用平面直角坐标系解决直线与圆的位置关系;
3.会用“数形结合”的数学思想解决问题.
复习:
(1)直线方程有几种形式?分别为什么?
(2)圆的方程有几种形式?分别是哪些?
(3)求圆的方程时,什么条件下,用标准方程?什么条件下用一般方程?
(4)如何用直线和圆的方程判断它们之间的位置关系?
(5)如何根据圆的方程,判断它们之间的位置关系?
求直线l:2x-y-2=0被圆C:(x-3)?+y?=9所截得的弦长。
前提测试:
知识探究:直线与圆的方程在实际生活中的应用
问题Ⅰ:一艘轮船在沿直线返回港口的途中,接到气象台的台风预报:台风中心位于轮船正西70 km处, 受影响的范围是半径长为30km的圆形区域. 已知港口位于台风中心正北40 km处,如果这艘轮船不改变航线,那么它是否会受到台风的影响?
轮船
港口
台风
思考1:解决这个问题的本质是什么?
思考2:你有什么办法判断轮船航线是否经过台风圆域?
轮船
港口
台风
x
y
o
思考3:如图所示建立直角坐标系,取10km为长度单位,那么轮船航线所在直线和台风圆域边界所在圆的方程分别是什么?
思考4:直线4x+7y-28=0与圆x2+y2=9的位置关系如何?对问题Ⅰ应作怎样的回答?
轮船
港口
台风
第一步:建立适当的平面直角坐标系,用坐标和方程表示问题中的几何元素,将平面几何问题转化为代数问题;
第二步:通过代数运算,解决代数问题;
第三步:将代数运算结果“翻译”成几何结论.
问题Ⅱ:如图是某圆拱形桥一孔圆拱的示意图. 这个圆的圆拱跨度AB=20m,拱高OP=4m,建造时每间隔4m需要用一根支柱支撑,求支柱A2P2的高度(精确到0.01m)
A
B
A1
A2
A3
A4
O
P
P2
思考1:你能用几何法求支柱A2P2的高度吗?
思考2:如图所示建立直角坐标系,那么求支柱A2P2的高度,化归为求一个什么问题?
A
B
A1
A2
A3
A4
O
P
P2
x
y
思考4:利用这个圆的方程可求得点P2的纵坐标是多少?问题Ⅱ的答案如何?
思考3:取1m为长度单位,如何求圆拱所在圆的方程?
x2+(y+10.5)2=14.52
A
B
A1
A2
A3
A4
O
P
P2
x
y
巩固练习:
某圆拱桥的水面跨度20m,拱高4m,现有一船,宽10m,水面以上高3m,这条船能否从桥下通过?
知识探究:直线与圆的方程在平面几何中的应用
问题Ⅲ:已知内接于圆的四边形的对角线互相垂直,求证:圆心到一边的距离等于这条边所对边长的一半.
思考1:许多平面几何问题常利用“坐标法”来解决,首先要做的工作是建立适当的直角坐标系,在本题中应如何选取坐标系?
X
y
o
思考2:如图所示建立直角坐标系,设四边形的四个顶点分别为点 A(a,0),B(0,b),C(c,0), D(0,d),那么BC边的长为多少?
A
B
C
D
M
x
y
o
N
思考3:四边形ABCD的外接圆圆心M的坐标如何?
思考4:如何计算圆心M到直线AD的距离|MN|?
A
B
C
D
M
x
y
o
N
课堂小结:
第一步:建立适当的平面直角坐标系,用坐标和方程表示问题中的几何元素,将平面几何问题转化为代数问题;
第二步:通过代数运算,解决代数问题;
第三步:将代数运算结果“翻译”成几何结论.
作业:
课本133页第7,8,9,10题
再见!
