高中数学人教A版必修二1.1.1 柱、锥、台、球的结构特征课件-(24张PPT)
文档属性
| 名称 | 高中数学人教A版必修二1.1.1 柱、锥、台、球的结构特征课件-(24张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-20 19:05:07 | ||
图片预览



文档简介
高一数学-必修2-第一章第一节
课题:空间几何体的
结构特征(一)
知识探究(一):空间几何体的类型
定义:如果我们只考虑这些物体的形状和大小,而不考虑其他因素,那么由这些抽象出来的空间图形就叫做空间几何体.
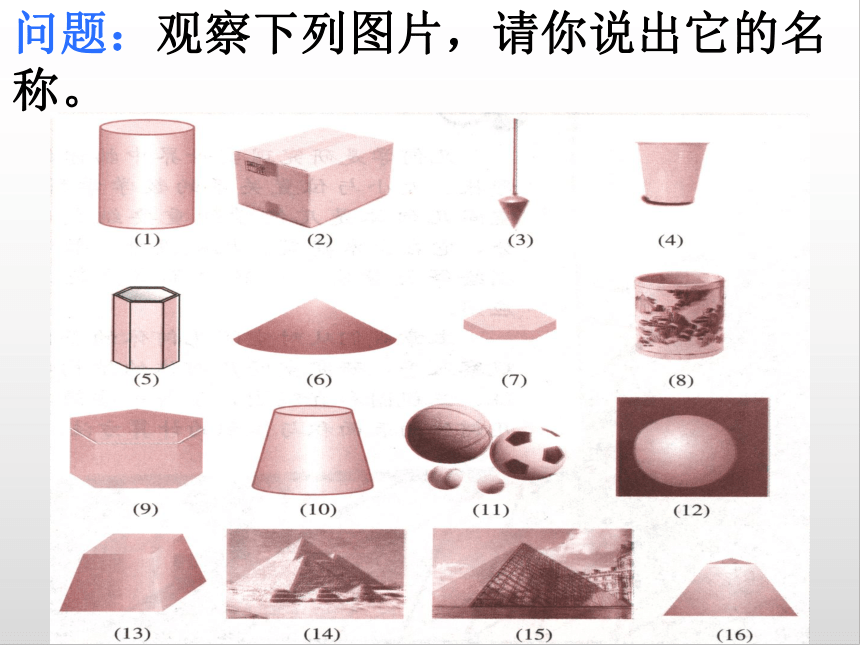
问题:观察下列图片,请你说出它的名称。
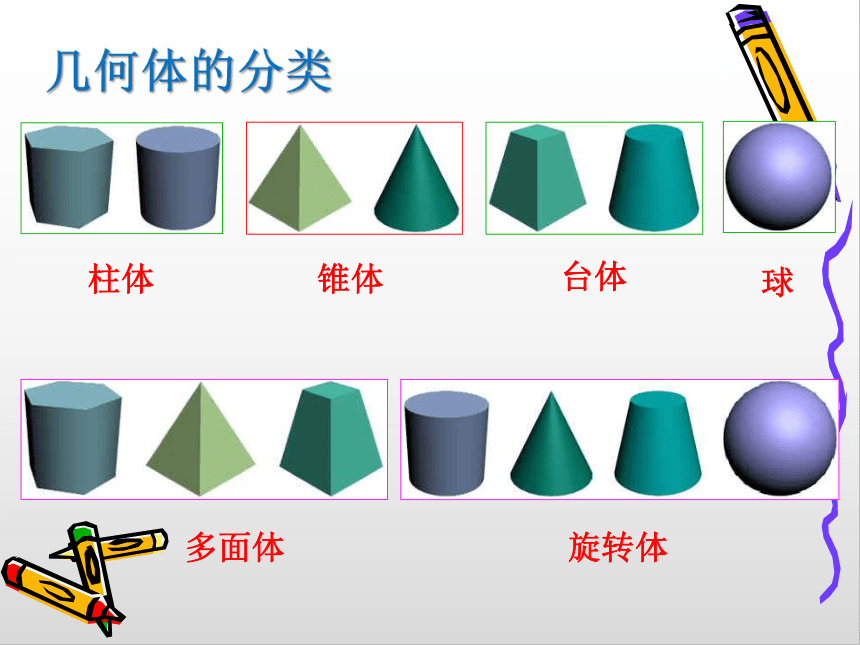
几何体的分类
柱体
锥体
台体
球
多面体
旋转体
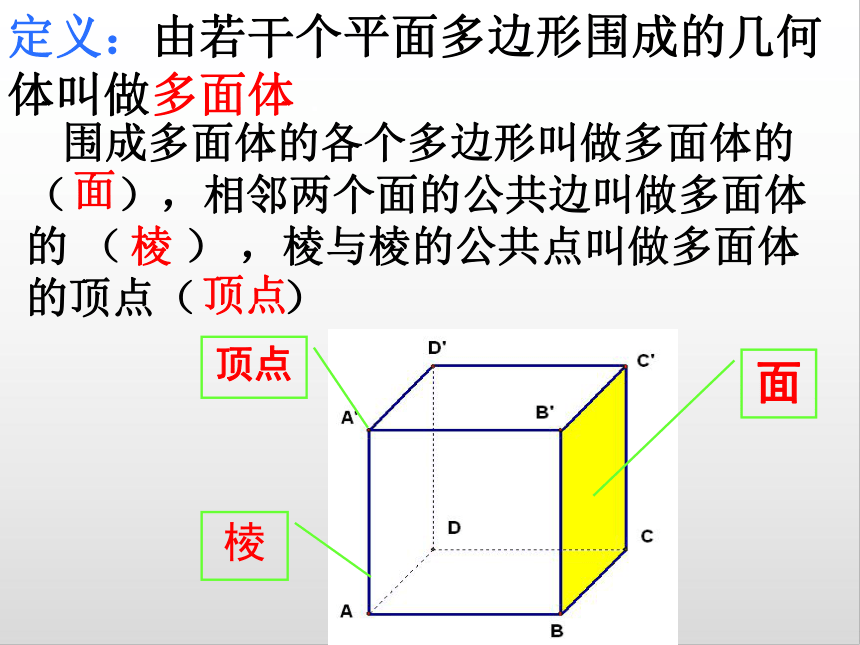
定义:由若干个平面多边形围成的几何体叫做多面体 .
面
顶点
棱
围成多面体的各个多边形叫做多面体的 ( ),相邻两个面的公共边叫做多面体的 ( ) ,棱与棱的公共点叫做多面体的顶点( )
面
棱
顶点
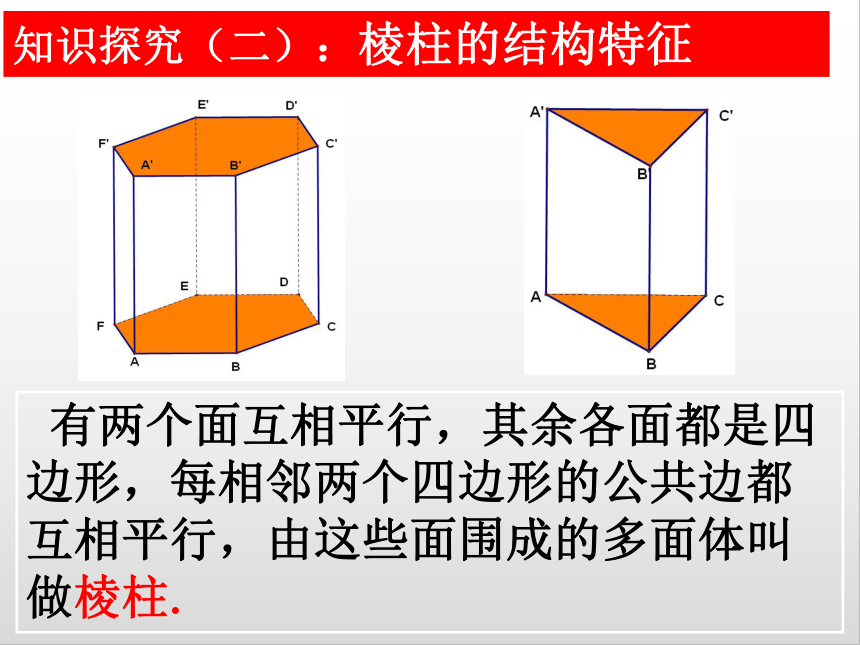
知识探究(二):棱柱的结构特征
有两个面互相平行,其余各面都是四边形,每相邻两个四边形的公共边都互相平行,由这些面围成的多面体叫做棱柱.
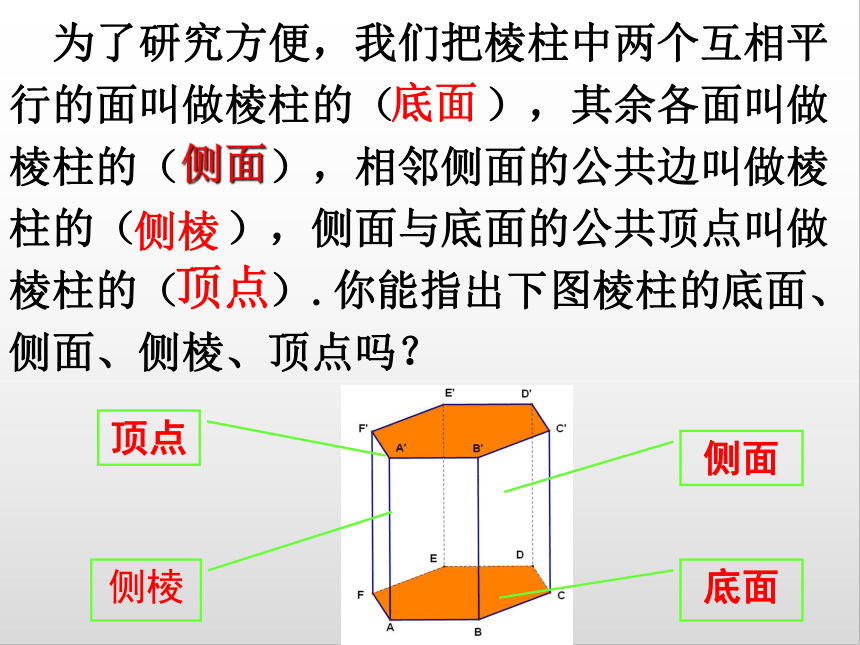
为了研究方便,我们把棱柱中两个互相平行的面叫做棱柱的( ),其余各面叫做棱柱的( ),相邻侧面的公共边叫做棱柱的( ),侧面与底面的公共顶点叫做棱柱的( ).你能指出下图棱柱的底面、侧面、侧棱、顶点吗?
侧面
顶点
侧棱
底面
底面
侧面
侧棱
顶点
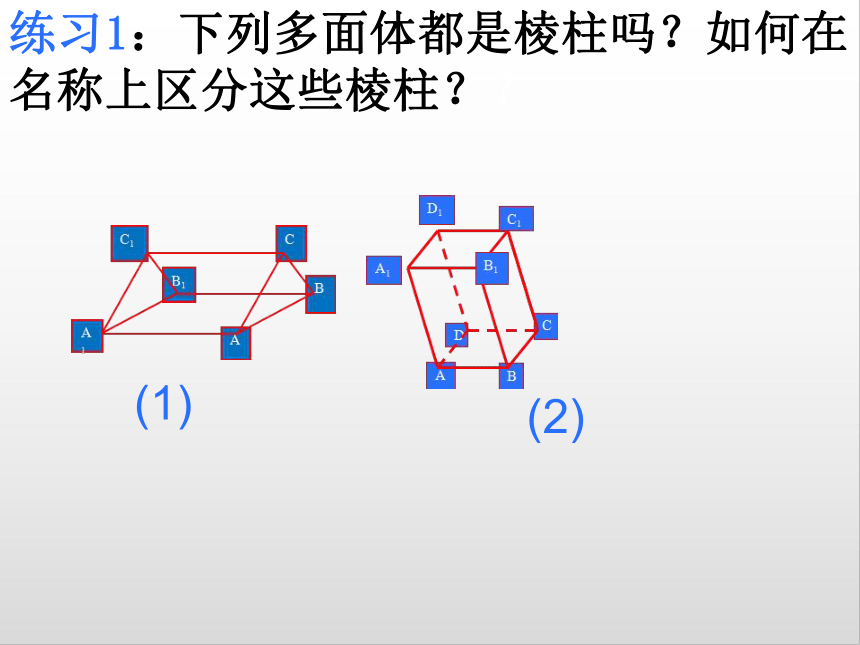
练习1:下列多面体都是棱柱吗?如何在名称上区分这些棱柱??
(1)
(2)
练习2: 如图,截面BCEF将长方体分割成两部分,这两部分是否为棱柱?
知识探究(三): 棱锥的结构特征
通过观察,这些多面体均由平面图形围成,其中一个面是( )其余各面都是( )并且这些三角形有一个公共( )
请同学们看这两幅图,根据它们的形状找出模型中与它们相类似的图形.
多边形
三角形
顶点
参照棱柱的说法,请你在图中找出棱锥的底面、侧面、侧棱、和顶点。
侧面
顶点
侧棱
底面
有一个面是多边形,其余各面都是有一个公共顶点的三角形,由这些面围成的多面体叫做棱锥.
练习3:下列多面体都是棱锥吗?如何命名?
(1)
(2)
(3)
知识探究(四):棱台的结构特征
用一个平行于棱锥底面的平面去截棱锥,底面与截面之间的部分形成一个多面体,这样的多面体叫做棱台.
参照棱柱的说法,请你在下图中找出棱台的底面、侧面、侧棱、和顶点。
侧面
上底面
侧棱
下底面
顶点
练习4:下列几何体是不是棱台,为什么?
(1)
(2)
知识探究(五):圆柱的结构特征
以矩形的一边所在
直线为旋转轴,其
余三边旋转形成的
面所围成的旋转体叫做圆柱.
A
A′
O
O′
旋转轴
底面
侧面
母线
在圆柱的形成中,旋转轴叫做圆柱的轴,垂直于轴的边旋转而成的圆面叫做圆柱的底面,平行于轴的边旋转而成的曲面叫做圆柱的侧面,平行于轴的边在旋转中的任何位置叫做圆柱侧面的母线.
侧面
轴
母线
底面
母线
生活中的圆柱
知识探究(六):圆锥的结构特征
定义:以直角三角形的一条直角边所在直线为旋转轴,其余两边旋转形成的面所围成的旋转体叫做圆锥
顶点
底面
轴
侧面
S
O
母线
A
B
定义:用一个平行于圆锥底面的平面去截圆锥,截面与底面之间的部分叫做圆台.圆台可以由什么平面图形旋转而形成?
知识探究(七):圆台的结构特征
与圆柱和圆锥一样,圆台也有轴、底面、侧面、母线,请你在图中找出来。
侧面
上底面
下底面
母线
轴
A
B
O
半径
球心
定义:以半圆的直径所在直线为旋转轴,半圆面旋转一周形成的几何体.
球的表示方法:用表示球心的字母表示,如:“球O”
知识探究(八):球的结构特征
知识小结
简单几何体的结构特征
柱体
锥体
台体
球
棱柱
圆柱
棱锥
圆锥
棱台
圆台
柱体
锥体
台体
球
圆柱
棱锥
圆锥
棱台
圆台
课题:空间几何体的
结构特征(一)
知识探究(一):空间几何体的类型
定义:如果我们只考虑这些物体的形状和大小,而不考虑其他因素,那么由这些抽象出来的空间图形就叫做空间几何体.
问题:观察下列图片,请你说出它的名称。
几何体的分类
柱体
锥体
台体
球
多面体
旋转体
定义:由若干个平面多边形围成的几何体叫做多面体 .
面
顶点
棱
围成多面体的各个多边形叫做多面体的 ( ),相邻两个面的公共边叫做多面体的 ( ) ,棱与棱的公共点叫做多面体的顶点( )
面
棱
顶点
知识探究(二):棱柱的结构特征
有两个面互相平行,其余各面都是四边形,每相邻两个四边形的公共边都互相平行,由这些面围成的多面体叫做棱柱.
为了研究方便,我们把棱柱中两个互相平行的面叫做棱柱的( ),其余各面叫做棱柱的( ),相邻侧面的公共边叫做棱柱的( ),侧面与底面的公共顶点叫做棱柱的( ).你能指出下图棱柱的底面、侧面、侧棱、顶点吗?
侧面
顶点
侧棱
底面
底面
侧面
侧棱
顶点
练习1:下列多面体都是棱柱吗?如何在名称上区分这些棱柱??
(1)
(2)
练习2: 如图,截面BCEF将长方体分割成两部分,这两部分是否为棱柱?
知识探究(三): 棱锥的结构特征
通过观察,这些多面体均由平面图形围成,其中一个面是( )其余各面都是( )并且这些三角形有一个公共( )
请同学们看这两幅图,根据它们的形状找出模型中与它们相类似的图形.
多边形
三角形
顶点
参照棱柱的说法,请你在图中找出棱锥的底面、侧面、侧棱、和顶点。
侧面
顶点
侧棱
底面
有一个面是多边形,其余各面都是有一个公共顶点的三角形,由这些面围成的多面体叫做棱锥.
练习3:下列多面体都是棱锥吗?如何命名?
(1)
(2)
(3)
知识探究(四):棱台的结构特征
用一个平行于棱锥底面的平面去截棱锥,底面与截面之间的部分形成一个多面体,这样的多面体叫做棱台.
参照棱柱的说法,请你在下图中找出棱台的底面、侧面、侧棱、和顶点。
侧面
上底面
侧棱
下底面
顶点
练习4:下列几何体是不是棱台,为什么?
(1)
(2)
知识探究(五):圆柱的结构特征
以矩形的一边所在
直线为旋转轴,其
余三边旋转形成的
面所围成的旋转体叫做圆柱.
A
A′
O
O′
旋转轴
底面
侧面
母线
在圆柱的形成中,旋转轴叫做圆柱的轴,垂直于轴的边旋转而成的圆面叫做圆柱的底面,平行于轴的边旋转而成的曲面叫做圆柱的侧面,平行于轴的边在旋转中的任何位置叫做圆柱侧面的母线.
侧面
轴
母线
底面
母线
生活中的圆柱
知识探究(六):圆锥的结构特征
定义:以直角三角形的一条直角边所在直线为旋转轴,其余两边旋转形成的面所围成的旋转体叫做圆锥
顶点
底面
轴
侧面
S
O
母线
A
B
定义:用一个平行于圆锥底面的平面去截圆锥,截面与底面之间的部分叫做圆台.圆台可以由什么平面图形旋转而形成?
知识探究(七):圆台的结构特征
与圆柱和圆锥一样,圆台也有轴、底面、侧面、母线,请你在图中找出来。
侧面
上底面
下底面
母线
轴
A
B
O
半径
球心
定义:以半圆的直径所在直线为旋转轴,半圆面旋转一周形成的几何体.
球的表示方法:用表示球心的字母表示,如:“球O”
知识探究(八):球的结构特征
知识小结
简单几何体的结构特征
柱体
锥体
台体
球
棱柱
圆柱
棱锥
圆锥
棱台
圆台
柱体
锥体
台体
球
圆柱
棱锥
圆锥
棱台
圆台
