人教版A版(2019)高中数学必修第一册4.2.1指数函数的概念说课课件 (1)30张PPT
文档属性
| 名称 | 人教版A版(2019)高中数学必修第一册4.2.1指数函数的概念说课课件 (1)30张PPT |  | |
| 格式 | pptx | ||
| 文件大小 | 6.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-20 19:10:35 | ||
图片预览










文档简介
指数函数的概念说课
目
录
CONTENTS
01
教材分析
05
教法、学法
02
学情分析
06
教学过程
03
目标分析
07
板书设计
04
重、难点分析
08
教学反思
教材分析
教材分析
学情分析
目标分析
重难点分析
教法学法
教学过程
板书设计
教学反思
承前启后
本节课是在上一章学习了函数的概念和基本性质,类比于研究幂函数的过程和方法、并已经掌握了指数幂运算的基础上,所做的进一步探究。
学情分析
目标分析
重难点分析
教法学法
教学过程
板书设计
教学反思
教材分析
学情分析
原有认知:学生在初中已经初步掌握了研究函数的基本方法,通过几何与函数概念的学习后具备了数形结合的思想。
现有认知:学生已经初步掌握了函数的基本性质和简单的指数运算技能。
心理特征:高一学生的思维能力正在由形象经验型向抽象理论型转变,能够用简单的化归思想去解决问题。
目标分析
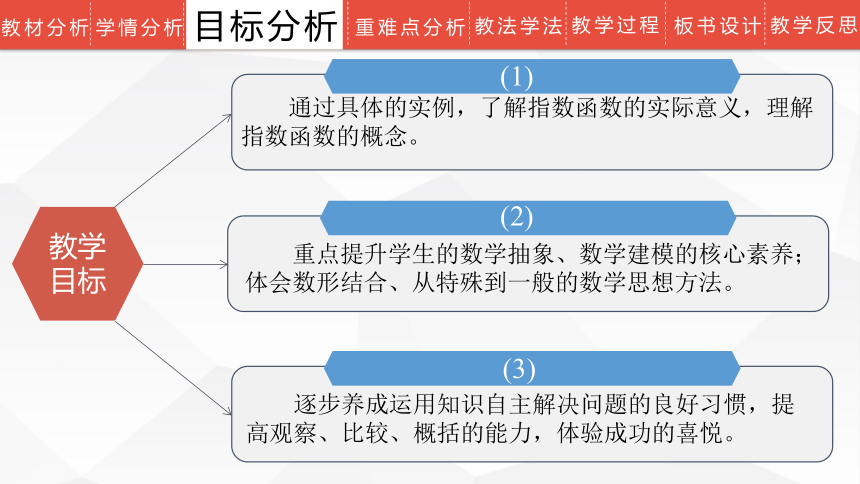
教学目标
(2)
重点提升学生的数学抽象、数学建模的核心素养;体会数形结合、从特殊到一般的数学思想方法。
(1)
通过具体的实例,了解指数函数的实际意义,理解指数函数的概念。
(3)
逐步养成运用知识自主解决问题的良好习惯,提高观察、比较、概括的能力,体验成功的喜悦。
学情分析
重难点分析
教法学法
教学过程
板书设计
教学反思
教材分析
目标分析
重、难点分析
学情分析
目标分析
教法学法
教学过程
板书设计
教学反思
教材分析
重难点分析
重 点
难 点
了解指数函数概念的实际意义,理解指数函数的概念,体会指数函数增长和衰减的规律。
由具体实例抽象出指数函数,理解指数函数的概念。
教法、学法
学情分析
目标分析
重难点分析
板书设计
教学反思
教材分析
教法学法
教学过程
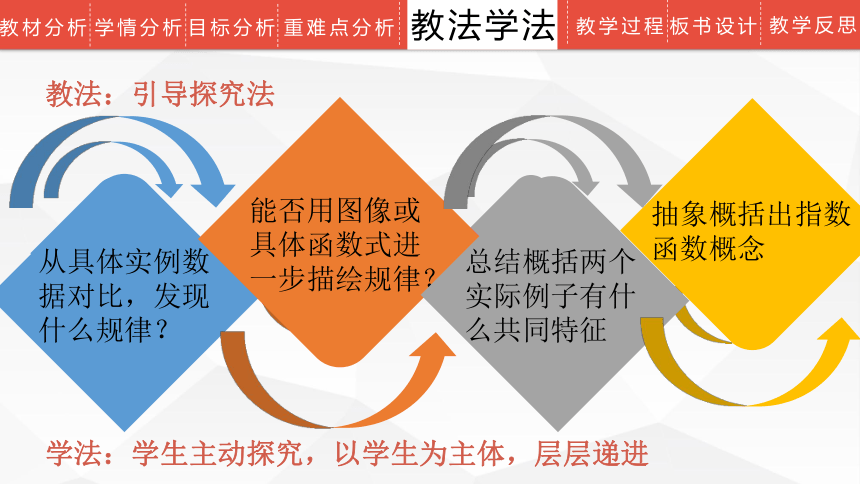
教法:引导探究法
1
2
3
4
从具体实例数据对比,发现什么规律?
能否用图像或具体函数式进一步描绘规律?
总结概括两个实际例子有什么共同特征
抽象概括出指数函数概念
学法:学生主动探究,以学生为主体,层层递进
教学过程
学情分析
目标分析
重难点分析
教法学法
教学反思
教材分析
教学过程
板书设计
教学
过程
创设情景,导入新知
01
深入研究,理解新知
02
强化训练,巩固小结
03
学情分析
目标分析
重难点分析
教法学法
教学反思
教材分析
教学过程
板书设计
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}时间/年
A地景区
B地景区
人次/万次
年增量/万次
人次/万次
年增量/万次
2001
600
278
2002
609
9
309
31
2003
620
11
344
35
2004
631
11
383
39
2005
641
10
427
44
2006
650
9
475
48
2007
661
11
528
53
2008
671
10
588
60
2009
681
10
655
67
2010
691
10
729
74
2011
702
11
811
82
2012
711
9
903
92
2013
721
10
1005
102
2014
732
11
1118
113
2015
743
11
1244
126
引例 -1
B地则取消了景区门票
A地提高了景区门票价格
随着中过经济高速增长,人民生活水平不断提高,旅游城了越来越多家庭的重要生活方式,由于旅游人数不断增加,A、B两地景区自2011年起采取了不同的应对措施,A提高了景区门票的价格,而B地则取消了景区门票。
问题1:比较两地景区游客人次的变化情况,你发现了怎样的变化规律?
问题2:能否作出A、B两地游客人次变化的图像?
创设情境,导入新知
学情分析
目标分析
重难点分析
教法学法
教学反思
教材分析
教学过程
板书设计
A地
B地
问题3:当年增量不能刻画B地的景区游客人次变化规律,能不能换一个量来刻画?比如‘增长率’即从2002年起将B地游客人次除以上一年的游客人次,看看能发现什么规律?
问题4:能否求出B地景区游客人次随时间变化的函数解析式,并根据解析式说明两地景区游客人次变化的情况?
2002年游客人次2001年游客人次=309278≈1.11
2003年游客人次2002年游客人次=344309≈1.11
2015年游客人次2014年游客人次=12441118≈1.11
。。。。。。
近似描述为
y=1.11????(????∈[0,+∞))
如果设经过x年后的游客人次为2001年的y倍,那么
学情分析
目标分析
重难点分析
教法学法
教学反思
教材分析
教学过程
板书设计
引例 -2
当生物死亡后,它机体内原有的碳14含量会按确定的衰减比率(简称衰减率)衰减,大约经过30年衰减为原来的一半,这个时间称为半衰期。
问题1:按照上述变化规律,生物体内碳14 含量与死亡年数之间有怎样的关系?
问题2:能否求出生物体内碳14含量随死亡年数变化的函数解析式?
问题3:生物死亡后体内碳14 含量每年衰减的比例是多少?
学情分析
目标分析
重难点分析
教法学法
教学反思
教材分析
教学过程
板书设计
引例 -2
y=((12)15730)????(????∈[0,+∞)
问题1:按照上述变化规律,生物体内碳14 含量与死亡年数之间有怎样的关系?
问题2:能否求出生物体内碳14含量随死亡年数变化的函数解析式?
问题3:生物死亡后体内碳14 含量每年衰减的比例是多少?
设计意图:通过对两个实际问题的探究,引出用函数刻画实际问题,并体会其增长和衰减规律,为抽象出指数函数作准备。
学情分析
目标分析
重难点分析
教法学法
教学反思
教材分析
教学过程
板书设计
深入研究,理解新知
学情分析
目标分析
重难点分析
教法学法
教学反思
教材分析
教学过程
板书设计
y=((12)15730)????(????∈[0,+∞)
y=1.11????(????∈[0,+∞))
①总结函数共同特征
②用a代替底数
学情分析
目标分析
重难点分析
教法学法
教学反思
教材分析
教学过程
板书设计
y=((12)15730)????(????∈[0,+∞)
y=1.11????(????∈[0,+∞))
①总结函数共同特征
②用a代替底数
③统一为y=????????,其中????为自变量
一般地,函数y=ax(a>0,且a≠1)叫做指数函数,其中指数x为自变量,定义域为R。
④强调a的取值范围
学情分析
目标分析
重难点分析
教法学法
教学反思
教材分析
教学过程
板书设计
y=((12)15730)????(????∈[0,+∞)
y=1.11????(????∈[0,+∞))
①总结函数共同特征
②用a代替底数
③统一为y=????????,其中????为自变量
一般地,函数y=ax(a>0,且a≠1)叫做指数函数,其中指数x为自变量,定义域为R。
④强调a的取值范围
设计意图:通过分析比较两个实例,概括它们的共同本质特征,从而得到指数函数的概念的本质属性,得出指数函数的概念。
学情分析
目标分析
重难点分析
教法学法
教学反思
教材分析
教学过程
板书设计
练习 -1
y=4x
y=x4
y=-4x
y=(-4)x
y=????????
y=(1????)????
判断下列那些函数是指数函数
由具体实例数据到简单描绘关于实例数据图像,总结规律特点,体会数形结合思想方法。
由具体实例抽象为具体函数、再由具体函数概括为指数函数的过程,提升数学抽象素养。
由具体实例中的函数关系总结归纳出指数函数形式,体会由特殊到一般的思想方法。
对实际问题进行数学抽象,用数形结合思想构建模型,体现数学建模的核心素养。
归纳
小结
学情分析
目标分析
重难点分析
教法学法
教学反思
教材分析
教学过程
板书设计
学情分析
目标分析
重难点分析
教法学法
教学反思
教材分析
教学过程
板书设计
课后练习
思考题:如果某函数值呈指数增长,那么称函数值增长为原来二倍所用的时间为“倍增期”,你可以给出一个倍增的指数函数模型实例么?
必做题
选做题
板书设计
学情分析
目标分析
重难点分析
教法学法
教学过程
教材分析
板书设计
教学反思
ppt展示
教学反思
THANK YOU!
学校名称:哈尔滨师范大学
报告人:李佳宁
学情分析
目标分析
重难点分析
教法学法
教学过程
板书设计
教材分析
教学反思
目
录
CONTENTS
01
教材分析
05
教法、学法
02
学情分析
06
教学过程
03
目标分析
07
板书设计
04
重、难点分析
08
教学反思
教材分析
教材分析
学情分析
目标分析
重难点分析
教法学法
教学过程
板书设计
教学反思
承前启后
本节课是在上一章学习了函数的概念和基本性质,类比于研究幂函数的过程和方法、并已经掌握了指数幂运算的基础上,所做的进一步探究。
学情分析
目标分析
重难点分析
教法学法
教学过程
板书设计
教学反思
教材分析
学情分析
原有认知:学生在初中已经初步掌握了研究函数的基本方法,通过几何与函数概念的学习后具备了数形结合的思想。
现有认知:学生已经初步掌握了函数的基本性质和简单的指数运算技能。
心理特征:高一学生的思维能力正在由形象经验型向抽象理论型转变,能够用简单的化归思想去解决问题。
目标分析
教学目标
(2)
重点提升学生的数学抽象、数学建模的核心素养;体会数形结合、从特殊到一般的数学思想方法。
(1)
通过具体的实例,了解指数函数的实际意义,理解指数函数的概念。
(3)
逐步养成运用知识自主解决问题的良好习惯,提高观察、比较、概括的能力,体验成功的喜悦。
学情分析
重难点分析
教法学法
教学过程
板书设计
教学反思
教材分析
目标分析
重、难点分析
学情分析
目标分析
教法学法
教学过程
板书设计
教学反思
教材分析
重难点分析
重 点
难 点
了解指数函数概念的实际意义,理解指数函数的概念,体会指数函数增长和衰减的规律。
由具体实例抽象出指数函数,理解指数函数的概念。
教法、学法
学情分析
目标分析
重难点分析
板书设计
教学反思
教材分析
教法学法
教学过程
教法:引导探究法
1
2
3
4
从具体实例数据对比,发现什么规律?
能否用图像或具体函数式进一步描绘规律?
总结概括两个实际例子有什么共同特征
抽象概括出指数函数概念
学法:学生主动探究,以学生为主体,层层递进
教学过程
学情分析
目标分析
重难点分析
教法学法
教学反思
教材分析
教学过程
板书设计
教学
过程
创设情景,导入新知
01
深入研究,理解新知
02
强化训练,巩固小结
03
学情分析
目标分析
重难点分析
教法学法
教学反思
教材分析
教学过程
板书设计
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}时间/年
A地景区
B地景区
人次/万次
年增量/万次
人次/万次
年增量/万次
2001
600
278
2002
609
9
309
31
2003
620
11
344
35
2004
631
11
383
39
2005
641
10
427
44
2006
650
9
475
48
2007
661
11
528
53
2008
671
10
588
60
2009
681
10
655
67
2010
691
10
729
74
2011
702
11
811
82
2012
711
9
903
92
2013
721
10
1005
102
2014
732
11
1118
113
2015
743
11
1244
126
引例 -1
B地则取消了景区门票
A地提高了景区门票价格
随着中过经济高速增长,人民生活水平不断提高,旅游城了越来越多家庭的重要生活方式,由于旅游人数不断增加,A、B两地景区自2011年起采取了不同的应对措施,A提高了景区门票的价格,而B地则取消了景区门票。
问题1:比较两地景区游客人次的变化情况,你发现了怎样的变化规律?
问题2:能否作出A、B两地游客人次变化的图像?
创设情境,导入新知
学情分析
目标分析
重难点分析
教法学法
教学反思
教材分析
教学过程
板书设计
A地
B地
问题3:当年增量不能刻画B地的景区游客人次变化规律,能不能换一个量来刻画?比如‘增长率’即从2002年起将B地游客人次除以上一年的游客人次,看看能发现什么规律?
问题4:能否求出B地景区游客人次随时间变化的函数解析式,并根据解析式说明两地景区游客人次变化的情况?
2002年游客人次2001年游客人次=309278≈1.11
2003年游客人次2002年游客人次=344309≈1.11
2015年游客人次2014年游客人次=12441118≈1.11
。。。。。。
近似描述为
y=1.11????(????∈[0,+∞))
如果设经过x年后的游客人次为2001年的y倍,那么
学情分析
目标分析
重难点分析
教法学法
教学反思
教材分析
教学过程
板书设计
引例 -2
当生物死亡后,它机体内原有的碳14含量会按确定的衰减比率(简称衰减率)衰减,大约经过30年衰减为原来的一半,这个时间称为半衰期。
问题1:按照上述变化规律,生物体内碳14 含量与死亡年数之间有怎样的关系?
问题2:能否求出生物体内碳14含量随死亡年数变化的函数解析式?
问题3:生物死亡后体内碳14 含量每年衰减的比例是多少?
学情分析
目标分析
重难点分析
教法学法
教学反思
教材分析
教学过程
板书设计
引例 -2
y=((12)15730)????(????∈[0,+∞)
问题1:按照上述变化规律,生物体内碳14 含量与死亡年数之间有怎样的关系?
问题2:能否求出生物体内碳14含量随死亡年数变化的函数解析式?
问题3:生物死亡后体内碳14 含量每年衰减的比例是多少?
设计意图:通过对两个实际问题的探究,引出用函数刻画实际问题,并体会其增长和衰减规律,为抽象出指数函数作准备。
学情分析
目标分析
重难点分析
教法学法
教学反思
教材分析
教学过程
板书设计
深入研究,理解新知
学情分析
目标分析
重难点分析
教法学法
教学反思
教材分析
教学过程
板书设计
y=((12)15730)????(????∈[0,+∞)
y=1.11????(????∈[0,+∞))
①总结函数共同特征
②用a代替底数
学情分析
目标分析
重难点分析
教法学法
教学反思
教材分析
教学过程
板书设计
y=((12)15730)????(????∈[0,+∞)
y=1.11????(????∈[0,+∞))
①总结函数共同特征
②用a代替底数
③统一为y=????????,其中????为自变量
一般地,函数y=ax(a>0,且a≠1)叫做指数函数,其中指数x为自变量,定义域为R。
④强调a的取值范围
学情分析
目标分析
重难点分析
教法学法
教学反思
教材分析
教学过程
板书设计
y=((12)15730)????(????∈[0,+∞)
y=1.11????(????∈[0,+∞))
①总结函数共同特征
②用a代替底数
③统一为y=????????,其中????为自变量
一般地,函数y=ax(a>0,且a≠1)叫做指数函数,其中指数x为自变量,定义域为R。
④强调a的取值范围
设计意图:通过分析比较两个实例,概括它们的共同本质特征,从而得到指数函数的概念的本质属性,得出指数函数的概念。
学情分析
目标分析
重难点分析
教法学法
教学反思
教材分析
教学过程
板书设计
练习 -1
y=4x
y=x4
y=-4x
y=(-4)x
y=????????
y=(1????)????
判断下列那些函数是指数函数
由具体实例数据到简单描绘关于实例数据图像,总结规律特点,体会数形结合思想方法。
由具体实例抽象为具体函数、再由具体函数概括为指数函数的过程,提升数学抽象素养。
由具体实例中的函数关系总结归纳出指数函数形式,体会由特殊到一般的思想方法。
对实际问题进行数学抽象,用数形结合思想构建模型,体现数学建模的核心素养。
归纳
小结
学情分析
目标分析
重难点分析
教法学法
教学反思
教材分析
教学过程
板书设计
学情分析
目标分析
重难点分析
教法学法
教学反思
教材分析
教学过程
板书设计
课后练习
思考题:如果某函数值呈指数增长,那么称函数值增长为原来二倍所用的时间为“倍增期”,你可以给出一个倍增的指数函数模型实例么?
必做题
选做题
板书设计
学情分析
目标分析
重难点分析
教法学法
教学过程
教材分析
板书设计
教学反思
ppt展示
教学反思
THANK YOU!
学校名称:哈尔滨师范大学
报告人:李佳宁
学情分析
目标分析
重难点分析
教法学法
教学过程
板书设计
教材分析
教学反思
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
