冀教版八年级数学下册第20章《函数》同步测试题(附答案)
文档属性
| 名称 | 冀教版八年级数学下册第20章《函数》同步测试题(附答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 411.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-20 09:55:40 | ||
图片预览


文档简介
函数的初步应用
一、选择题
1.下列命题中错误的是()
A.在等速运动公式s=vt中,v是常量
B.在用公式C=2R计算不同的半径所对应的周长C时,C,R是变量,2是常量
C.练习本定价0.5元/个,买x个本子付款y元,它们的关系可以表示成y=0.5x,这里的x为自然数
D.今有360本图书借给学生阅读,每人9本,则余下书数y(本)与学生数x(个)间的关系为y=360-9x,其自变量x的取值范围是0≤x<40
2.在下列等式中,y是x的函数的有(
)
3x-2y=0,x2-y2=1,y=,y=,x=
A.1个B.2个C.3个D.
4个
3.下面函数关系式中分别注明了自变量的取值范围:
①圆的面积公式A=r2
(r为正实数)
②多边形对角线条数l=,(n为整数)
③y=
(x为不等于5的实数)
④
(x为任意实数)
这些说明中正确的是(
)
A.①和②B.①和③C.①和④D.②和③
4.一根蜡烛长20cm,点燃后每小时燃烧5cm,燃烧时剩下的高度h(cm)与燃烧时间t(h)之间的函数关系式用图像表示为(
)
5.弹簧的长度与所挂物体的质量的关系为一次函数,如图所示,y为弹簧的长度,x为所挂物体的质量,由图可知,每挂lkg物体时,弹簧伸长
(
)
A.0.5cm B.7.5cm
C.lcm
D.不能确定
二、填空题
6.全国每年都有大量土地被沙漠吞没,改造沙漠、保护土地资源已经成为一项十分紧迫的任务.某地区现有土地面积100万平方千米,沙漠面积200万平方千米,土地沙漠化的变化情况如图所示.
(1)如果不采取任何措施,那么到第5年底,该地区沙漠面积将新增加
万平方千米.
(2)如果该地区沙漠的面积继续按此趋势扩大,那么从现在开始,第
年底后,该地区将丧失土地资源。
(3)如果从现在开始采取植树造林等措施,每年改造4万平方千米沙漠,那么到第
年底,该地区的沙漠面积能减少到176万平方千米。
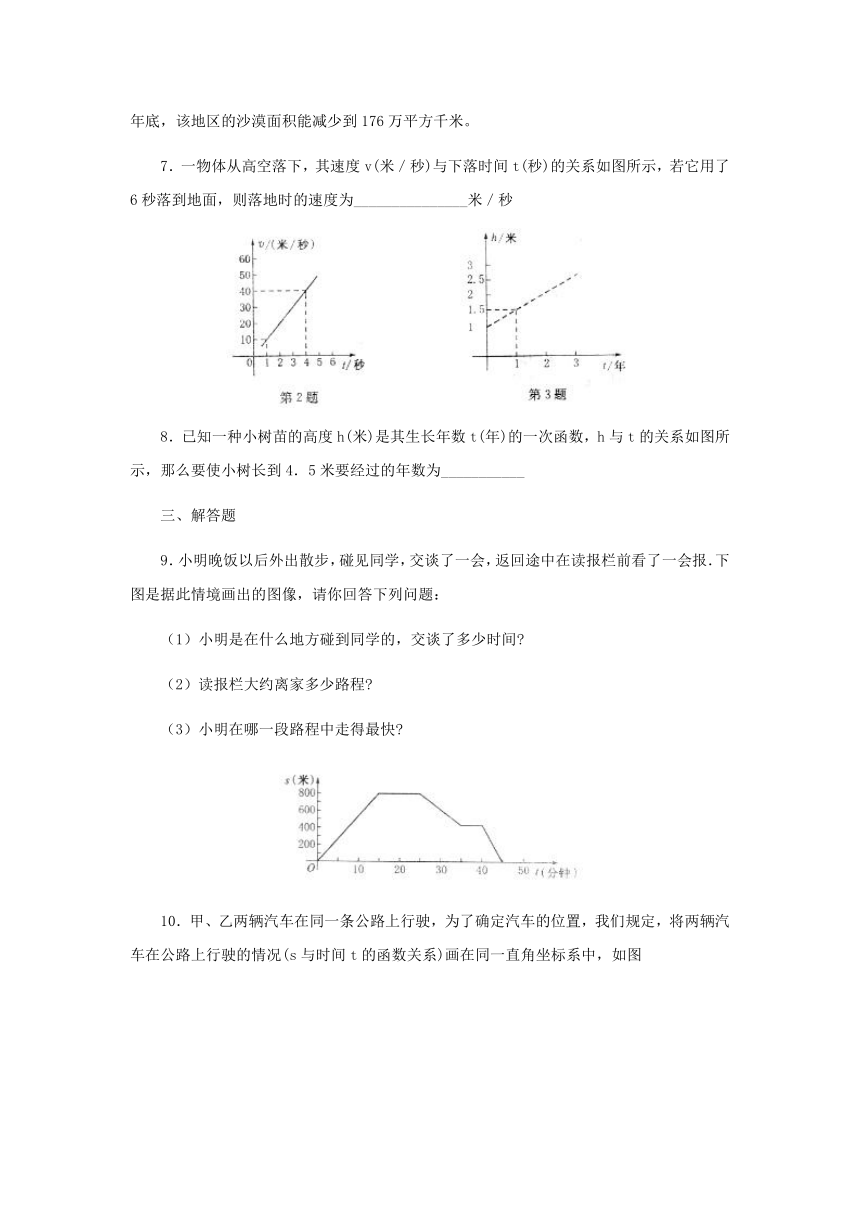
7.一物体从高空落下,其速度v(米/秒)与下落时间t(秒)的关系如图所示,若它用了6秒落到地面,则落地时的速度为_______________米/秒
8.已知一种小树苗的高度h(米)是其生长年数t(年)的一次函数,h与t的关系如图所示,那么要使小树长到4.5米要经过的年数为___________
三、解答题
9.小明晚饭以后外出散步,碰见同学,交谈了一会,返回途中在读报栏前看了一会报.下图是据此情境画出的图像,请你回答下列问题:
(1)小明是在什么地方碰到同学的,交谈了多少时间?
(2)读报栏大约离家多少路程?
(3)小明在哪一段路程中走得最快?
10.甲、乙两辆汽车在同一条公路上行驶,为了确定汽车的位置,我们规定,将两辆汽车在公路上行驶的情况(s与时间t的函数关系)画在同一直角坐标系中,如图
(1)根据图像判断汽车在这条公路上行驶的状况,并填在下表中.
行驶方向
速度大小(km/h)
出发前的位置
甲车
乙车
(2)甲、乙两车能否相遇?如能相遇,说出相遇时刻及在公路上的位置;如不能相遇,请说明理由.
能力提高
11.一根弹簧原长12cm,每挂1kg物体弹簧伸长+cm,弹簧挂物重最多不超过15kg.
(1)写出弹簧长度ycm与物重xkg的函数关系式.
(2)写出自变量的取值范围.
(3)求出挂l0kg重物时,弹簧的长度.
12.如图,在矩形ABCD中,AB=4,BC=7,P是BC边上与B点不重合的动点,过点P的直线交CD的延长线于R,交AD于Q(Q与D不重合),且∠RPC=45°,设BP=x,梯形AB-PQ的面积为y,求y与x之间的函数关系,并求出自变量x的取值范围.
13.某市自来水公司为了鼓励市民节约用水,采用了分段收费标准.若每户居民每月应交水费y(元)是用水量x(t)的函数,其图像如图所示.
(1)分别写出x≤5和x>5时,y与x的函数关系式.
(2)观察函数图像,回答自来水公司采取的收费标准.
(3)若某户居民该月用水3.5t,则应交水费多少元?若该月交水费9元,则用水多少t?
答案
l.
A
2.D
3.C
4.B
5.C
6.(1)离家800米处
交谈了10分钟
(2)读报栏大约离家400米
(3)从读报栏回到家那段路程。
7.提示:(1)要判断汽车行驶状况,需要分别求出甲、乙两车s与t的关系式.可由甲射线经过点(3,80)和点(5,0)求得关系式为s=-40t+200.由乙射线经过点(0,-70)和点(3,80)求得s=50t-70.所以甲车向x轴负方向行驶,速度为40km/h,出发前在0km刻度右侧200km处;乙车向x轴正方向行驶,速度为50km/h,出发前在0km刻度的左侧70km处.
(2)两车3小时时相遇,地点在0km刻度的右侧80km处。
8.A
9.(1)当x≤5时,函数图像经过原点,故是正比例函数,设为y=k1x,x=5时y=3.6,故有3.6=5kl,k1=0.72,所以当x≤5时,函数关系式为y=0.72x;当x>5时,直线经过点(5,3.6)和点(8,6.3),设直线关系式为y=k2x+b,有3.6=5k2+b……①,6.3=8k2+b……②,由①得b=3.6-5k2,由②得b=6.3-8k2,所以3.6-5k2=6.3-8k2,即k2=0.9.把k2=0.9代人①得b=-0.9,所以当x>5时,函数关系式为y=0.9x-0.9.
(2)收费标准为用水量低于5t(含5t),每吨交费0.72元,若用水量超过5t,则超过部分每吨交水费0.9元.
(3)当x=3.5时,未超过5t,y=0.72×3.5=2.52(元);当y=9元时,用水超过5t,由9=0.9x-0.9得x=11(t).
一、选择题
1.下列命题中错误的是()
A.在等速运动公式s=vt中,v是常量
B.在用公式C=2R计算不同的半径所对应的周长C时,C,R是变量,2是常量
C.练习本定价0.5元/个,买x个本子付款y元,它们的关系可以表示成y=0.5x,这里的x为自然数
D.今有360本图书借给学生阅读,每人9本,则余下书数y(本)与学生数x(个)间的关系为y=360-9x,其自变量x的取值范围是0≤x<40
2.在下列等式中,y是x的函数的有(
)
3x-2y=0,x2-y2=1,y=,y=,x=
A.1个B.2个C.3个D.
4个
3.下面函数关系式中分别注明了自变量的取值范围:
①圆的面积公式A=r2
(r为正实数)
②多边形对角线条数l=,(n为整数)
③y=
(x为不等于5的实数)
④
(x为任意实数)
这些说明中正确的是(
)
A.①和②B.①和③C.①和④D.②和③
4.一根蜡烛长20cm,点燃后每小时燃烧5cm,燃烧时剩下的高度h(cm)与燃烧时间t(h)之间的函数关系式用图像表示为(
)
5.弹簧的长度与所挂物体的质量的关系为一次函数,如图所示,y为弹簧的长度,x为所挂物体的质量,由图可知,每挂lkg物体时,弹簧伸长
(
)
A.0.5cm B.7.5cm
C.lcm
D.不能确定
二、填空题
6.全国每年都有大量土地被沙漠吞没,改造沙漠、保护土地资源已经成为一项十分紧迫的任务.某地区现有土地面积100万平方千米,沙漠面积200万平方千米,土地沙漠化的变化情况如图所示.
(1)如果不采取任何措施,那么到第5年底,该地区沙漠面积将新增加
万平方千米.
(2)如果该地区沙漠的面积继续按此趋势扩大,那么从现在开始,第
年底后,该地区将丧失土地资源。
(3)如果从现在开始采取植树造林等措施,每年改造4万平方千米沙漠,那么到第
年底,该地区的沙漠面积能减少到176万平方千米。
7.一物体从高空落下,其速度v(米/秒)与下落时间t(秒)的关系如图所示,若它用了6秒落到地面,则落地时的速度为_______________米/秒
8.已知一种小树苗的高度h(米)是其生长年数t(年)的一次函数,h与t的关系如图所示,那么要使小树长到4.5米要经过的年数为___________
三、解答题
9.小明晚饭以后外出散步,碰见同学,交谈了一会,返回途中在读报栏前看了一会报.下图是据此情境画出的图像,请你回答下列问题:
(1)小明是在什么地方碰到同学的,交谈了多少时间?
(2)读报栏大约离家多少路程?
(3)小明在哪一段路程中走得最快?
10.甲、乙两辆汽车在同一条公路上行驶,为了确定汽车的位置,我们规定,将两辆汽车在公路上行驶的情况(s与时间t的函数关系)画在同一直角坐标系中,如图
(1)根据图像判断汽车在这条公路上行驶的状况,并填在下表中.
行驶方向
速度大小(km/h)
出发前的位置
甲车
乙车
(2)甲、乙两车能否相遇?如能相遇,说出相遇时刻及在公路上的位置;如不能相遇,请说明理由.
能力提高
11.一根弹簧原长12cm,每挂1kg物体弹簧伸长+cm,弹簧挂物重最多不超过15kg.
(1)写出弹簧长度ycm与物重xkg的函数关系式.
(2)写出自变量的取值范围.
(3)求出挂l0kg重物时,弹簧的长度.
12.如图,在矩形ABCD中,AB=4,BC=7,P是BC边上与B点不重合的动点,过点P的直线交CD的延长线于R,交AD于Q(Q与D不重合),且∠RPC=45°,设BP=x,梯形AB-PQ的面积为y,求y与x之间的函数关系,并求出自变量x的取值范围.
13.某市自来水公司为了鼓励市民节约用水,采用了分段收费标准.若每户居民每月应交水费y(元)是用水量x(t)的函数,其图像如图所示.
(1)分别写出x≤5和x>5时,y与x的函数关系式.
(2)观察函数图像,回答自来水公司采取的收费标准.
(3)若某户居民该月用水3.5t,则应交水费多少元?若该月交水费9元,则用水多少t?
答案
l.
A
2.D
3.C
4.B
5.C
6.(1)离家800米处
交谈了10分钟
(2)读报栏大约离家400米
(3)从读报栏回到家那段路程。
7.提示:(1)要判断汽车行驶状况,需要分别求出甲、乙两车s与t的关系式.可由甲射线经过点(3,80)和点(5,0)求得关系式为s=-40t+200.由乙射线经过点(0,-70)和点(3,80)求得s=50t-70.所以甲车向x轴负方向行驶,速度为40km/h,出发前在0km刻度右侧200km处;乙车向x轴正方向行驶,速度为50km/h,出发前在0km刻度的左侧70km处.
(2)两车3小时时相遇,地点在0km刻度的右侧80km处。
8.A
9.(1)当x≤5时,函数图像经过原点,故是正比例函数,设为y=k1x,x=5时y=3.6,故有3.6=5kl,k1=0.72,所以当x≤5时,函数关系式为y=0.72x;当x>5时,直线经过点(5,3.6)和点(8,6.3),设直线关系式为y=k2x+b,有3.6=5k2+b……①,6.3=8k2+b……②,由①得b=3.6-5k2,由②得b=6.3-8k2,所以3.6-5k2=6.3-8k2,即k2=0.9.把k2=0.9代人①得b=-0.9,所以当x>5时,函数关系式为y=0.9x-0.9.
(2)收费标准为用水量低于5t(含5t),每吨交费0.72元,若用水量超过5t,则超过部分每吨交水费0.9元.
(3)当x=3.5时,未超过5t,y=0.72×3.5=2.52(元);当y=9元时,用水超过5t,由9=0.9x-0.9得x=11(t).
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
