冀教版九年级数学下册 第29章 直线与圆的位置关系 单元测试卷(Word版 附答案)
文档属性
| 名称 | 冀教版九年级数学下册 第29章 直线与圆的位置关系 单元测试卷(Word版 附答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 121.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-20 00:00:00 | ||
图片预览


文档简介
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
冀教版九年级数学下册
第29章
直线与圆的位置关系
单元评估检测试卷
一、单选题(共9题;共27分)
1.已知⊙O的半径为4,圆心O到直线l的距离为3,则直线l与⊙O的位置关系是(
??)
A.?相交??????????????????????????????????B.?相切??????????????????????????????????C.?相离??????????????????????????????????D.?无法确定
2.如图,已知PA是⊙O的切线,A为切点,PC与⊙O相交于B.C两点,PB=2㎝,BC=8㎝,则PA的长等于(???????
)
A.?4㎝???????????????????????????????????B.?16㎝???????????????????????????????????C.?20㎝???????????????????????????????????D.?2㎝
3.⊙O的半径为5,圆心O到直线l的距离为6,则直线l与⊙O的位置关系是(??
)
A.?相交??????????????????????????????????B.?相切??????????????????????????????????C.?相离??????????????????????????????????D.?无法确定
4.已知⊙O的半径为5,点P到圆心O的距离为7,那么点P与⊙O的位置关系是( )
A.?点P在⊙O上??????????????????????B.?点P在⊙O内??????????????????????C.?点P在⊙O外??????????????????????D.?无法确定
5.在平面直角坐标系中,⊙P的圆心坐标为(4,8),半径为5,那么x轴与⊙P的位置关系是(??
)
A.?相交?????????????????????????????????B.?相离?????????????????????????????????C.?相切?????????????????????????????????D.?以上都不是
6.已知⊙O的半径是6,点O到直线l的距离为5,则直线l与⊙O的位置关系是(??
)
A.?相离??????????????????????????????????B.?相切??????????????????????????????????C.?相交??????????????????????????????????D.?无法判断
7.如图,正六边形ABCDEF中,P、Q两点分别为△ACF、△CEF的内心.若AF=2,则PQ的长度为何?( )
A.?1???????????????????????????????????B.?2???????????????????????????????????C.?2
﹣2???????????????????????????????????D.?4﹣2
8.如图,一个半径为r的圆形纸片在边长为a(
)的等边三角形内任意运动,则在该等边三角形内,这个圆形纸片“不能接触到的部分”的面积是(??
)
A.???????????????????????????????B.???????????????????????????????C.???????????????????????????????D.?πr2
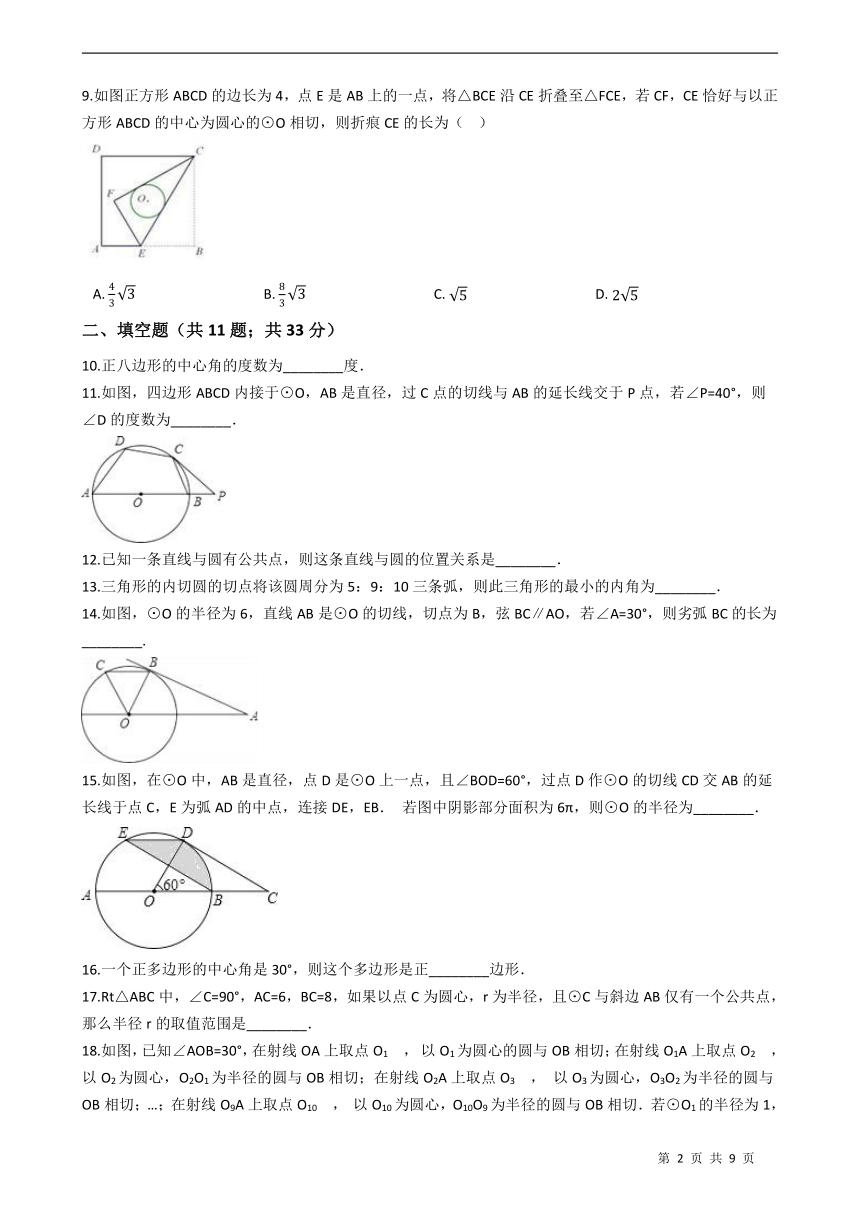
9.如图正方形ABCD的边长为4,点E是AB上的一点,将△BCE沿CE折叠至△FCE,若CF,CE恰好与以正方形ABCD的中心为圆心的⊙O相切,则折痕CE的长为(????)
A.??????????????????????????????????????B.??????????????????????????????????????C.??????????????????????????????????????D.?
二、填空题(共11题;共33分)
10.正八边形的中心角的度数为________度.
11.如图,四边形ABCD内接于⊙O,AB是直径,过C点的切线与AB的延长线交于P点,若∠P=40°,则∠D的度数为________.
12.已知一条直线与圆有公共点,则这条直线与圆的位置关系是________.
13.三角形的内切圆的切点将该圆周分为5:9:10三条弧,则此三角形的最小的内角为________.
14.如图,⊙O的半径为6,直线AB是⊙O的切线,切点为B,弦BC∥AO,若∠A=30°,则劣弧BC的长为
________.
15.如图,在⊙O中,AB是直径,点D是⊙O上一点,且∠BOD=60°,过点D作⊙O的切线CD交AB的延长线于点C,E为弧AD的中点,连接DE,EB.
若图中阴影部分面积为6π,则⊙O的半径为________.
16.一个正多边形的中心角是30°,则这个多边形是正________边形.
17.Rt△ABC中,∠C=90°,AC=6,BC=8,如果以点C为圆心,r为半径,且⊙C与斜边AB仅有一个公共点,那么半径r的取值范围是________.
18.如图,已知∠AOB=30°,在射线OA上取点O1
,
以O1为圆心的圆与OB相切;在射线O1A上取点O2
,
以O2为圆心,O2O1为半径的圆与OB相切;在射线O2A上取点O3
,
以O3为圆心,O3O2为半径的圆与OB相切;…;在射线O9A上取点O10
,
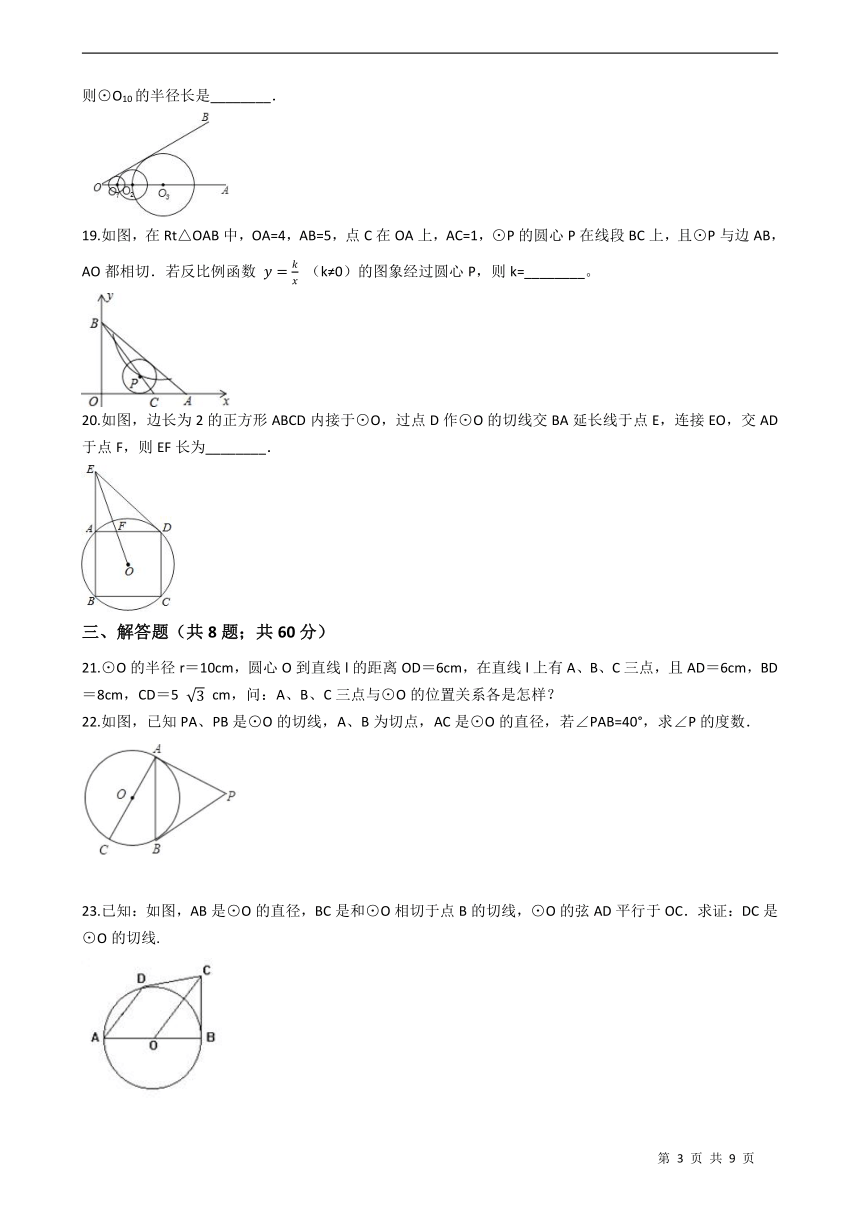
以O10为圆心,O10O9为半径的圆与OB相切.若⊙O1的半径为1,则⊙O10的半径长是________.
19.如图,在Rt△OAB中,OA=4,AB=5,点C在OA上,AC=1,⊙P的圆心P在线段BC上,且⊙P与边AB,AO都相切.若反比例函数
(k≠0)的图象经过圆心P,则k=________。
20.如图,边长为2的正方形ABCD内接于⊙O,过点D作⊙O的切线交BA延长线于点E,连接EO,交AD于点F,则EF长为________.
三、解答题(共8题;共60分)
21.⊙O的半径r=10cm,圆心O到直线l的距离OD=6cm,在直线l上有A、B、C三点,且AD=6cm,BD=8cm,CD=5
cm,问:A、B、C三点与⊙O的位置关系各是怎样?
22.如图,已知PA、PB是⊙O的切线,A、B为切点,AC是⊙O的直径,若∠PAB=40°,求∠P的度数.
23.已知:如图,AB是⊙O的直径,BC是和⊙O相切于点B的切线,⊙O的弦AD平行于OC.求证:DC是⊙O的切线.
24.如图AB是⊙O的切线,切点为B,AO交⊙O于点C,过点C作DC⊥OA,交AB于点D.
(1)求证:∠CDO=∠BDO;
(2)若∠A=30°,⊙O的半径为4,求阴影部分的面积(结果保留π).
25.如图,在△ABC中,∠ACB=90°,E为BC上一点,以CE为直径作⊙O,AB与⊙O相切于点D,连接CD,若BE=OE=2.
(1)求证:∠A=2∠DCB;
(2)求图中阴影部分的面积(结果保留和根号).
26.如图,BC为⊙O的直径,A为⊙O上的点,以BC、AB为边作?ABCD,⊙O交AD于点E,连结BE,点P为过点B的⊙O的切线上一点,连结PE,且满足∠PEA=∠ABE.
(1)求证:PB=PE;
(2)若sin∠P=
,
求的值.
27.△ABC的内切圆⊙o与BC,CA,AB分别相切于点D、E、F,且AB=9cm,BC=14cm,CA=13cm,求AF、BD、CE的长?
28.如图,AB为⊙O的直径,弦CD⊥AB,垂足为点E,CF⊥AF,且CF=CE.
(1)求证:CF是⊙O的切线;
(2)若sin∠BAC=
,
求的值
答案解析部分
一、单选题
1.【答案】A
2.【答案】D
3.【答案】C
4.【答案】C
5.【答案】B
6.【答案】C
7.【答案】C
8.【答案】C
9.【答案】B
二、填空题
10.【答案】45
11.【答案】115°
12.【答案】相切或相交
13.【答案】30°
14.【答案】2π
15.【答案】6
16.【答案】十二
17.【答案】r=4.8或6<r≤8
18.【答案】29
19.【答案】
20.【答案】
三、解答题
21.【答案】解:∵OA=
=
=
(cm)<r=10cm,
OB=
=
=10(cm)=r,
OC=
=
=
(cm)>r=10cm,
∴点A在⊙O内,点B在⊙O上,点C在⊙O外.
22.【答案】解:∵PA和PB为切线
,A,B是切点
∴PA=PB
∴∠PBA=∠PAB=40°
∴∠P=180°-(∠PAB+∠PBA)=100°.
23.【答案】证明:连接OD;
∵AD平行于OC,
∴∠COD=∠ODA,∠COB=∠A;
∵∠ODA=∠A,
∴∠COD=∠COB,OC=OC,OD=OB,
∴△OCD≌△OCB,
∴∠CDO=∠CBO=90°.
∴DC是⊙O的切线.
24.【答案】(1)证明:AB切⊙O于点B,
∴OB⊥AB,即∠B=90°.
又∴DC⊥OA,∴∠OCD=90°.
在Rt△COD与Rt△BOD中,OD=OD,OB=OC,
∴Rt△COD≌Rt△BOD.
∴∠CDO=∠BDO.
(2)解:在Rt△ABO中,∠A=30°,OB=4,
∴∠BOC=60°,
∵Rt△COD≌Rt△BOD,
∴∠BOD=30°,
∴BD=OB·tan
30°=.
∴S四边形OCDB=2S△OBD=2××4×=.
∵∠BOC=60°,
∴S扇形OBC==.
∴S阴影=S四边形OCDB-S扇形OBC=-.
25.【答案】(1)证明:连接OD.
∵AB与⊙O相切于点D,
∴
OD⊥AB,
∴∠B+∠DOB=90°.
∵∠ACB=90°,
∴∠A+∠B=90°,
∴∠A=∠DOB.
∵OC=OD,
∴∠DOB=2∠DCB.
∴∠A=2∠DCB.
(2)解:在Rt△ODB中,
∵OD=OE,OE=BE,
∴sin∠B=,
∴∠B=30°,∠DOB=60°.
∵BD=OB·sin60°=,
∴,SDOB=,S扇形ODE=.
∴S阴影=SDOB-S扇形ODE=.
?
26.【答案】解:(1)证明:∵PB是⊙O的切线,
∴∠ABP=∠AEB,
∵∠PEA=∠ABE.
∴∠PBE=∠PEB,
∴PB=PE;
(2)连接EC,延长DA交PB于F,
∵PB是⊙O的切线,
∴BC⊥PB,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴EF⊥PB,
∵sin∠P=,
设PE=5a,EF=3a,则PF=4a,
∵PB=PE=5a,
∴BF=a,
∴BE==a,
∴=,
∵AD∥BC,
∴=,
∴AB=CE,
∵AB=CD,
∴CE=CD,
∴∠D=∠CED,
∵AD∥BC,
∴∠AEB=∠EBC,
∵∠ABP=∠AEB,
∴∠ABP=∠EBC,
∴∠PBE=∠ABC,
∴∠PBE=∠D,
∵∠PBE=∠PEB,
∴△CDE∽△PBE,
∴==;
27.【答案】解:根据切线长定理,设AE=AF=xcm,BF=BD=ycm,CE=CD=zcm.
根据题意,得
,
解得:
?.
即AF=4cm、BD=5cm、CE=9cm
28.【答案】
(
第
6
页
共
9
页
)
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
冀教版九年级数学下册
第29章
直线与圆的位置关系
单元评估检测试卷
一、单选题(共9题;共27分)
1.已知⊙O的半径为4,圆心O到直线l的距离为3,则直线l与⊙O的位置关系是(
??)
A.?相交??????????????????????????????????B.?相切??????????????????????????????????C.?相离??????????????????????????????????D.?无法确定
2.如图,已知PA是⊙O的切线,A为切点,PC与⊙O相交于B.C两点,PB=2㎝,BC=8㎝,则PA的长等于(???????
)
A.?4㎝???????????????????????????????????B.?16㎝???????????????????????????????????C.?20㎝???????????????????????????????????D.?2㎝
3.⊙O的半径为5,圆心O到直线l的距离为6,则直线l与⊙O的位置关系是(??
)
A.?相交??????????????????????????????????B.?相切??????????????????????????????????C.?相离??????????????????????????????????D.?无法确定
4.已知⊙O的半径为5,点P到圆心O的距离为7,那么点P与⊙O的位置关系是( )
A.?点P在⊙O上??????????????????????B.?点P在⊙O内??????????????????????C.?点P在⊙O外??????????????????????D.?无法确定
5.在平面直角坐标系中,⊙P的圆心坐标为(4,8),半径为5,那么x轴与⊙P的位置关系是(??
)
A.?相交?????????????????????????????????B.?相离?????????????????????????????????C.?相切?????????????????????????????????D.?以上都不是
6.已知⊙O的半径是6,点O到直线l的距离为5,则直线l与⊙O的位置关系是(??
)
A.?相离??????????????????????????????????B.?相切??????????????????????????????????C.?相交??????????????????????????????????D.?无法判断
7.如图,正六边形ABCDEF中,P、Q两点分别为△ACF、△CEF的内心.若AF=2,则PQ的长度为何?( )
A.?1???????????????????????????????????B.?2???????????????????????????????????C.?2
﹣2???????????????????????????????????D.?4﹣2
8.如图,一个半径为r的圆形纸片在边长为a(
)的等边三角形内任意运动,则在该等边三角形内,这个圆形纸片“不能接触到的部分”的面积是(??
)
A.???????????????????????????????B.???????????????????????????????C.???????????????????????????????D.?πr2
9.如图正方形ABCD的边长为4,点E是AB上的一点,将△BCE沿CE折叠至△FCE,若CF,CE恰好与以正方形ABCD的中心为圆心的⊙O相切,则折痕CE的长为(????)
A.??????????????????????????????????????B.??????????????????????????????????????C.??????????????????????????????????????D.?
二、填空题(共11题;共33分)
10.正八边形的中心角的度数为________度.
11.如图,四边形ABCD内接于⊙O,AB是直径,过C点的切线与AB的延长线交于P点,若∠P=40°,则∠D的度数为________.
12.已知一条直线与圆有公共点,则这条直线与圆的位置关系是________.
13.三角形的内切圆的切点将该圆周分为5:9:10三条弧,则此三角形的最小的内角为________.
14.如图,⊙O的半径为6,直线AB是⊙O的切线,切点为B,弦BC∥AO,若∠A=30°,则劣弧BC的长为
________.
15.如图,在⊙O中,AB是直径,点D是⊙O上一点,且∠BOD=60°,过点D作⊙O的切线CD交AB的延长线于点C,E为弧AD的中点,连接DE,EB.
若图中阴影部分面积为6π,则⊙O的半径为________.
16.一个正多边形的中心角是30°,则这个多边形是正________边形.
17.Rt△ABC中,∠C=90°,AC=6,BC=8,如果以点C为圆心,r为半径,且⊙C与斜边AB仅有一个公共点,那么半径r的取值范围是________.
18.如图,已知∠AOB=30°,在射线OA上取点O1
,
以O1为圆心的圆与OB相切;在射线O1A上取点O2
,
以O2为圆心,O2O1为半径的圆与OB相切;在射线O2A上取点O3
,
以O3为圆心,O3O2为半径的圆与OB相切;…;在射线O9A上取点O10
,
以O10为圆心,O10O9为半径的圆与OB相切.若⊙O1的半径为1,则⊙O10的半径长是________.
19.如图,在Rt△OAB中,OA=4,AB=5,点C在OA上,AC=1,⊙P的圆心P在线段BC上,且⊙P与边AB,AO都相切.若反比例函数
(k≠0)的图象经过圆心P,则k=________。
20.如图,边长为2的正方形ABCD内接于⊙O,过点D作⊙O的切线交BA延长线于点E,连接EO,交AD于点F,则EF长为________.
三、解答题(共8题;共60分)
21.⊙O的半径r=10cm,圆心O到直线l的距离OD=6cm,在直线l上有A、B、C三点,且AD=6cm,BD=8cm,CD=5
cm,问:A、B、C三点与⊙O的位置关系各是怎样?
22.如图,已知PA、PB是⊙O的切线,A、B为切点,AC是⊙O的直径,若∠PAB=40°,求∠P的度数.
23.已知:如图,AB是⊙O的直径,BC是和⊙O相切于点B的切线,⊙O的弦AD平行于OC.求证:DC是⊙O的切线.
24.如图AB是⊙O的切线,切点为B,AO交⊙O于点C,过点C作DC⊥OA,交AB于点D.
(1)求证:∠CDO=∠BDO;
(2)若∠A=30°,⊙O的半径为4,求阴影部分的面积(结果保留π).
25.如图,在△ABC中,∠ACB=90°,E为BC上一点,以CE为直径作⊙O,AB与⊙O相切于点D,连接CD,若BE=OE=2.
(1)求证:∠A=2∠DCB;
(2)求图中阴影部分的面积(结果保留和根号).
26.如图,BC为⊙O的直径,A为⊙O上的点,以BC、AB为边作?ABCD,⊙O交AD于点E,连结BE,点P为过点B的⊙O的切线上一点,连结PE,且满足∠PEA=∠ABE.
(1)求证:PB=PE;
(2)若sin∠P=
,
求的值.
27.△ABC的内切圆⊙o与BC,CA,AB分别相切于点D、E、F,且AB=9cm,BC=14cm,CA=13cm,求AF、BD、CE的长?
28.如图,AB为⊙O的直径,弦CD⊥AB,垂足为点E,CF⊥AF,且CF=CE.
(1)求证:CF是⊙O的切线;
(2)若sin∠BAC=
,
求的值
答案解析部分
一、单选题
1.【答案】A
2.【答案】D
3.【答案】C
4.【答案】C
5.【答案】B
6.【答案】C
7.【答案】C
8.【答案】C
9.【答案】B
二、填空题
10.【答案】45
11.【答案】115°
12.【答案】相切或相交
13.【答案】30°
14.【答案】2π
15.【答案】6
16.【答案】十二
17.【答案】r=4.8或6<r≤8
18.【答案】29
19.【答案】
20.【答案】
三、解答题
21.【答案】解:∵OA=
=
=
(cm)<r=10cm,
OB=
=
=10(cm)=r,
OC=
=
=
(cm)>r=10cm,
∴点A在⊙O内,点B在⊙O上,点C在⊙O外.
22.【答案】解:∵PA和PB为切线
,A,B是切点
∴PA=PB
∴∠PBA=∠PAB=40°
∴∠P=180°-(∠PAB+∠PBA)=100°.
23.【答案】证明:连接OD;
∵AD平行于OC,
∴∠COD=∠ODA,∠COB=∠A;
∵∠ODA=∠A,
∴∠COD=∠COB,OC=OC,OD=OB,
∴△OCD≌△OCB,
∴∠CDO=∠CBO=90°.
∴DC是⊙O的切线.
24.【答案】(1)证明:AB切⊙O于点B,
∴OB⊥AB,即∠B=90°.
又∴DC⊥OA,∴∠OCD=90°.
在Rt△COD与Rt△BOD中,OD=OD,OB=OC,
∴Rt△COD≌Rt△BOD.
∴∠CDO=∠BDO.
(2)解:在Rt△ABO中,∠A=30°,OB=4,
∴∠BOC=60°,
∵Rt△COD≌Rt△BOD,
∴∠BOD=30°,
∴BD=OB·tan
30°=.
∴S四边形OCDB=2S△OBD=2××4×=.
∵∠BOC=60°,
∴S扇形OBC==.
∴S阴影=S四边形OCDB-S扇形OBC=-.
25.【答案】(1)证明:连接OD.
∵AB与⊙O相切于点D,
∴
OD⊥AB,
∴∠B+∠DOB=90°.
∵∠ACB=90°,
∴∠A+∠B=90°,
∴∠A=∠DOB.
∵OC=OD,
∴∠DOB=2∠DCB.
∴∠A=2∠DCB.
(2)解:在Rt△ODB中,
∵OD=OE,OE=BE,
∴sin∠B=,
∴∠B=30°,∠DOB=60°.
∵BD=OB·sin60°=,
∴,SDOB=,S扇形ODE=.
∴S阴影=SDOB-S扇形ODE=.
?
26.【答案】解:(1)证明:∵PB是⊙O的切线,
∴∠ABP=∠AEB,
∵∠PEA=∠ABE.
∴∠PBE=∠PEB,
∴PB=PE;
(2)连接EC,延长DA交PB于F,
∵PB是⊙O的切线,
∴BC⊥PB,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴EF⊥PB,
∵sin∠P=,
设PE=5a,EF=3a,则PF=4a,
∵PB=PE=5a,
∴BF=a,
∴BE==a,
∴=,
∵AD∥BC,
∴=,
∴AB=CE,
∵AB=CD,
∴CE=CD,
∴∠D=∠CED,
∵AD∥BC,
∴∠AEB=∠EBC,
∵∠ABP=∠AEB,
∴∠ABP=∠EBC,
∴∠PBE=∠ABC,
∴∠PBE=∠D,
∵∠PBE=∠PEB,
∴△CDE∽△PBE,
∴==;
27.【答案】解:根据切线长定理,设AE=AF=xcm,BF=BD=ycm,CE=CD=zcm.
根据题意,得
,
解得:
?.
即AF=4cm、BD=5cm、CE=9cm
28.【答案】
(
第
6
页
共
9
页
)
