冀教版九年级数学下册 第30章 二次函数 单元评估检测试卷(Word版 附答案)
文档属性
| 名称 | 冀教版九年级数学下册 第30章 二次函数 单元评估检测试卷(Word版 附答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 99.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-20 00:00:00 | ||
图片预览



文档简介
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
冀教版九年级数学下册
第30章
二次函数
单元评估检测试卷
一、单选题(共10题;共30分)
1.已知二次函数的解析式为,则该二次函数图象的顶点坐标是(???)
A.?(-2,1)??????????????????????????????B.?(2,1)??????????????????????????????C.?(2,-1)??????????????????????????????D.?(1,2)
2.抛物线y=x2﹣3x+2与y轴交点的坐标为(??
)
A.?(0,2)??????????????????????????B.?(1,0)??????????????????????????C.?(2,0)??????????????????????????D.?(0,﹣3)
3.下列函数:①
;
②
;③
;④
,其中
的值随
值的增大而增大的函数有(??
)
.
?
A.?4个??????????????????????????????????????B.?3个??????????????????????????????????????C.?2个??????????????????????????????????????D.?1个
4.(2017?兰州)下表是一组二次函数y=x2+3x﹣5的自变量x与函数值y的对应值:
?x
?1
?1.1
?1.2
?1.3
?1.4
?y
﹣1
﹣0.49
?0.04
?0.59
?1.16
那么方程x2+3x﹣5=0的一个近似根是(??
)
A.?1????????????????????????????????????????B.?1.1????????????????????????????????????????C.?1.2????????????????????????????????????????D.?1.3
5.如图,二次函数y=ax2+bx+c的图象与x轴交于(﹣2,0)和(4,0)两点,当函数值y>0时,自变量x的取值范围是(??
)
A.?x<﹣2????????????????????????????????B.?x>4????????????????????????????????C.?﹣2<x<4????????????????????????????????D.?x>0
6.二次函数图象的顶点坐标是(????)
A.?(-1,3)??????????????????????????????????B.?(1,3)??????????????????????????????????C.?(-1,-3)??????????????????????????????????D.?(1,-3)
7.已知学校航模组设计制作的火箭的升空高度h(m)与飞行时间t(s)满足函数表达式h=﹣t2+24t+1.则下列说法中正确的是(???
)
A.?点火后9s和点火后13s的升空高度相同????????????????B.?点火后24s火箭落于地面
C.?点火后10s的升空高度为139m????????????????????????????D.?火箭升空的最大高度为145m
8.二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=1,则下列四个结论错误的是(???)
A.?c>0????????????????????????????B.?2a+b=0????????????????????????????C.?b2-4ac>0????????????????????????????D.?a-b+c>0
9.在同一直角坐标系中,二次函数y=x2+2与一次函数y=2x的图象大致是( )
A.?????????????????????????B.?????????????????????????C.?????????????????????????D.?
10.二次函数y=ax2+bx+c(a≠0)的图象如图,下列四个结论:
①4a+c<0;②m(am+b)+b>a(m≠﹣1);③关于x的一元二次方程ax2+(b﹣1)x+c=0没有实数根;④ak4+bk2<a(k2+1)2+b(k2+1)(k为常数).其中正确结论的个数是(??
)
A.?4个???????????????????????????????????????B.?3个???????????????????????????????????????C.?2个???????????????????????????????????????D.?1个
二、填空题(共10题;共36分)
11.将二次函数y=2x2-1的图像沿y轴向上平移2个单位,所得图像对应的函数表达式为________.
12.抛物线y=ax2+bx﹣3经过点(1,1),则代数式a+b的值为________
13.已知y=
是关于x的二次函数,则a的值为________.
14.如图,是边长为1的正方形OABC绕顶点O顺时针旋转75°后得到的,原正方形的顶点A在x轴的正半轴上,此时点B恰好落在函数y=ax2(a<0)的图象上,则a的值为________.
15.已知抛物线y=ax2+bx经过点(﹣4,0),则这条抛物线的对称轴是________.
16.抛物线y=a(x+1)2经过点(﹣2,1),则a=________.
17.形如:y=ax2+bx+c(a≠0)的函数叫二次函数,它的图象是一条抛物线.类比一元一次方程的解可以看成两条直线的交点的横坐标;则一元二次方程x2+x﹣3=0的解可以看成抛物线y=x2+x﹣3与直线y=0(x轴)的交点的横坐标;也可以看成是抛物线y=x2与直线y=________
的交点的横坐标;也可以看成是抛物线y= ________?与直线y=﹣x的交点的横坐标;
18.抛物线y=﹣x2﹣2x+3与x轴交点为________,与y轴交点为________.
19.如图,已知抛物线y=x2+bx+c经过点(0,﹣3),请你确定一个b的值,使该抛物线与x轴的一个交点在(1,0)和(3,0)之间.你确定的b的值是________.
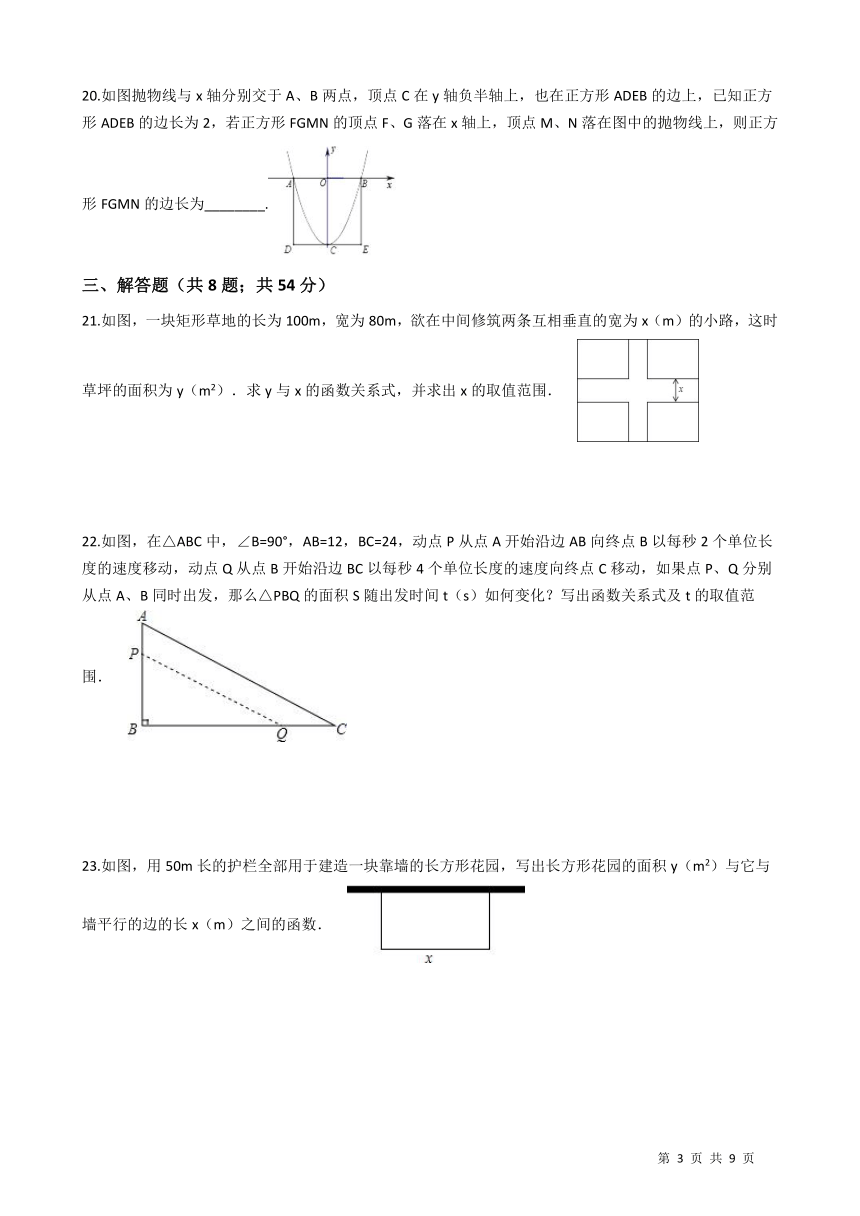
20.如图抛物线与x轴分别交于A、B两点,顶点C在y轴负半轴上,也在正方形ADEB的边上,已知正方形ADEB的边长为2,若正方形FGMN的顶点F、G落在x轴上,顶点M、N落在图中的抛物线上,则正方形FGMN的边长为________.
三、解答题(共8题;共54分)
21.如图,一块矩形草地的长为100m,宽为80m,欲在中间修筑两条互相垂直的宽为x(m)的小路,这时草坪的面积为y(m2).求y与x的函数关系式,并求出x的取值范围.
22.如图,在△ABC中,∠B=90°,AB=12,BC=24,动点P从点A开始沿边AB向终点B以每秒2个单位长度的速度移动,动点Q从点B开始沿边BC以每秒4个单位长度的速度向终点C移动,如果点P、Q分别从点A、B同时出发,那么△PBQ的面积S随出发时间t(s)如何变化?写出函数关系式及t的取值范围.
23.如图,用50m长的护栏全部用于建造一块靠墙的长方形花园,写出长方形花园的面积y(m2)与它与墙平行的边的长x(m)之间的函数.
24.在某市开展的环境创优活动中,某居民小区要在一块靠墙(墙长15米)的空地上修建一个矩形花园ABCD,花园的一边靠墙,另三边用总长为40m的栅栏围成,若设花园与墙平行的一边长为x(m),花园的面积为y(m2)。
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)满足条件的花园面积能达到200m2吗?若能,求出此时x的值,若不能,说明理由:
(3)根据(1)中求得的函数关系式,判断当x取何值时,花园的面积最大?最大面积是多少?
25.为鼓励大学毕业生自主创业,某市政府出台了相关政策:由政府协调,本市企业按成本价提供产品给大学毕业生自主销售,成本价与出厂价之间的差价由政府承担,李明按照相关政策投资销售本市生产的一种新型节能灯,已知这种节能灯的成本价为每件10元,出厂价为每件12元,每月销售量y(件)与销售单价x(元)之间的关系近似满足一次函数:y=-10x+500.
⑴李明在开始创业的第一个月将销售单价定为20元,那么政府这个月为他承担的总差价为多少元?
⑵设李明获得的利润为W(元),当销售单价定为多少元时,每月可获得最大利润?
⑶物价部门规定,这种节能灯的销售单价不得高于25元,如果李明想要每月获得的利润不低于3000元,那么政府为他承担的总差价最少为多少元?
26.在美化校园的活动中,某综合实践小组的同学借如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形的花圃ABCD(篱笆只围AB、BC两边)设AB=xm.
(1)若想围得花圃面积为192cm2
,
求x的值;
(2)若在点P处有一棵小树与墙CD、AD的距离分别为15m和6m,要将这棵树围在花圃内(含边界,不考虑树干的粗细),求花圃面积S的最大值.
27.(2017·金华)(本题8分)
甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分.
如图,甲
在O点正上方1m的P处发出一球,羽毛球飞行的高度y(m)与水平距离x(m)之间满足函数表达式
,已知点O与球网的水平距离为5m,球网的高度1.55m.
(1)当a=?
时,①求h的值.②通过计算判断此球能否过网.
(2)若甲发球过网后,羽毛球飞行到与点O的水平距离为7m,离地面的高度为
m的Q处时,乙扣球成功,求a的值.
28.如图,Rt△ABC中,∠C=90°,BC=6,AC=8.点P,Q都是斜边AB上的动点,点P从B
向A运动(不与点B重合),点Q从A向B运动,BP=AQ.点D,E分别是点A,B以Q,P为对称中心的对称点,
HQ⊥AB于Q,交AC于点H.当点E到达顶点A时,P,Q同时停止运动.设BP的长为x,△HDE的面积为y.
(1)求证:△DHQ∽△ABC;
(2)求y关于x的函数解析式并求y的最大值;
(3)当x为何值时,△HDE为等腰三角形?
答案解析部分
一、单选题
1.【答案】B
2.【答案】A
3.【答案】C
4.【答案】C
5.【答案】C
6.【答案】B
7.【答案】D
8.【答案】D
9.【答案】C
10.【答案】D
二、填空题
11.【答案】
12.【答案】4
13.【答案】?3
14.【答案】﹣
15.【答案】x=-2
16.【答案】1
17.【答案】﹣x+3;x2﹣3
18.【答案】(﹣3,0);(1,0);(0,3)
19.【答案】1(在﹣2<b<2范围内的任何一个数)
20.【答案】
三、解答题
21.【答案】解:设中间修筑两条互相垂直的宽为x(m)的小路,草坪的面积为y(m2),
根据题意得出:y=100﹣80﹣80x﹣100x+x2=x2﹣180x+8000(0<x<80)
22.【答案】解:△PBQ的面积S随出发时间t(s)成二次函数关系变化,
∵在△ABC中,∠B=90°,AB=12,BC=24,动点P从点A开始沿边AB向终点B以每秒2个单位长度的速度移动,
动点Q从点B开始沿边BC以每秒4个单位长度的速度向终点C移动,
∴BP=12﹣2t,BQ=4t,
∴△PBQ的面积S随出发时间t(s)的解析式为:y=
(12﹣2t)×4t=﹣4t2+24t,(0<t<6)
23.【答案】解:∵与墙平行的边的长为x(m),则垂直于墙的边长为:
?=(25﹣0.5x)m,
根据题意得出:y=x(25﹣0.5x)=﹣0.5x2+25x
24.【答案】解:(1)根据题意得:,
即y=﹣x2+20x(0<x≤15);
(2)当y=200时,即﹣x2+20x=200,
解得x1=x2=20>15,
∴花园面积不能达到200m2;
(3)∵y=﹣x2+20x的图象是开口向下的抛物线,对称轴为x=20,
∴当0<x≤15时,y随x的增大而增大.
∴x=15时,y有最大值,
y最大值=﹣×152+20×15=187.5m2
即当x=15时,花园的面积最大,最大面积为187.5m2
.
25.【答案】解:⑴当x=20时,y=-10x+500=-10×20+500=300,
300×(12-10)=300×2=600,
即政府这个月为他承担的总差价为600元.
⑵依题意得,W=(x-10)(-10x+500)=-10x2+600x-5000=-10(x-30)2+4000
∵a=-10<0,∴当x=30时,W有最大值4000.
即当销售单价定为30元时,每月可获得最大利润4000元.
⑶由题意得:-10x2+600x-5000=3000,解得:x1=20,x2=40.
∵a=-10<0,抛物线开口向下,
∴结合图象可知:当20≤x≤40时,W≥3000.
又∵x≤25,
∴当20≤x≤25时,W≥3000.
设政府每个月为他承担的总差价为p元,
∴p=(12-10)×(-10x+500)
=-20x+1000.
∵k=-20<0.
∴p随x的增大而减小,∴当x=25时,p有最小值500.
即销售单价定为25元时,政府每个月为他承担的总差价最少为500元.
26.【答案】(1)解:由题意得:x(28-x)=192,解此方程得x1=
12,x2=16
(2)解:花圃面积S=
x(28-x)=
-(x-14)2+196,
由题意知
,解得6≤x≤13,
在6≤x≤13的范围内,S随x增大而增大,
∴当x=13时,S最大值=-(13-14)2+196=195(m2).
27.【答案】(1)解:①∵a=?
,P(0,1);
∴1=
+h;
∴h=
;
②把x=5代入y=
得:
y==1.625;
∵1.625>1.55;
∴此球能过网.
(2)解:把(0,1),(7,
)代入y=a得:;
;解得:;
∴a=.
28.【答案】解:(1)∵A、D关于点Q成中心对称,HQ⊥AB,
∴HQD=C=90°,HD=HA,
∴HDQ=A,
∴△DHQ∽△ABC.
(2)①如图1,当0ED=10-4x,QH=AQtanA=x,
此时y=(10-4x)x=-x2+x..
当x=时,最大值y=.
②如图2,当时,
ED=4x-10,QH=AQtanA=x,
此时y=(4x-10)x=x2-x..
当x=5时,最大值y=.
∴y与x之间的函数解析式为y=
y的最大值是.
(3)①如图1,当0若DE=DH,∵DH=AH==x,
DE=10-4x,
∴10-4x=x,x=.
显然ED=EH,HD=HE不可能;
②如图2,当时,
若DE=DH,4x-10=x,x=;
若HD=HE,此时点D,E分别与点B,A重合,x=5;
若ED=EH,则△EDH∽△HDA,
∴,,x=.?
∴当x的值为,,5,,时,△HDE是等腰三角形
(
第
6
页
共
9
页
)
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
冀教版九年级数学下册
第30章
二次函数
单元评估检测试卷
一、单选题(共10题;共30分)
1.已知二次函数的解析式为,则该二次函数图象的顶点坐标是(???)
A.?(-2,1)??????????????????????????????B.?(2,1)??????????????????????????????C.?(2,-1)??????????????????????????????D.?(1,2)
2.抛物线y=x2﹣3x+2与y轴交点的坐标为(??
)
A.?(0,2)??????????????????????????B.?(1,0)??????????????????????????C.?(2,0)??????????????????????????D.?(0,﹣3)
3.下列函数:①
;
②
;③
;④
,其中
的值随
值的增大而增大的函数有(??
)
.
?
A.?4个??????????????????????????????????????B.?3个??????????????????????????????????????C.?2个??????????????????????????????????????D.?1个
4.(2017?兰州)下表是一组二次函数y=x2+3x﹣5的自变量x与函数值y的对应值:
?x
?1
?1.1
?1.2
?1.3
?1.4
?y
﹣1
﹣0.49
?0.04
?0.59
?1.16
那么方程x2+3x﹣5=0的一个近似根是(??
)
A.?1????????????????????????????????????????B.?1.1????????????????????????????????????????C.?1.2????????????????????????????????????????D.?1.3
5.如图,二次函数y=ax2+bx+c的图象与x轴交于(﹣2,0)和(4,0)两点,当函数值y>0时,自变量x的取值范围是(??
)
A.?x<﹣2????????????????????????????????B.?x>4????????????????????????????????C.?﹣2<x<4????????????????????????????????D.?x>0
6.二次函数图象的顶点坐标是(????)
A.?(-1,3)??????????????????????????????????B.?(1,3)??????????????????????????????????C.?(-1,-3)??????????????????????????????????D.?(1,-3)
7.已知学校航模组设计制作的火箭的升空高度h(m)与飞行时间t(s)满足函数表达式h=﹣t2+24t+1.则下列说法中正确的是(???
)
A.?点火后9s和点火后13s的升空高度相同????????????????B.?点火后24s火箭落于地面
C.?点火后10s的升空高度为139m????????????????????????????D.?火箭升空的最大高度为145m
8.二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=1,则下列四个结论错误的是(???)
A.?c>0????????????????????????????B.?2a+b=0????????????????????????????C.?b2-4ac>0????????????????????????????D.?a-b+c>0
9.在同一直角坐标系中,二次函数y=x2+2与一次函数y=2x的图象大致是( )
A.?????????????????????????B.?????????????????????????C.?????????????????????????D.?
10.二次函数y=ax2+bx+c(a≠0)的图象如图,下列四个结论:
①4a+c<0;②m(am+b)+b>a(m≠﹣1);③关于x的一元二次方程ax2+(b﹣1)x+c=0没有实数根;④ak4+bk2<a(k2+1)2+b(k2+1)(k为常数).其中正确结论的个数是(??
)
A.?4个???????????????????????????????????????B.?3个???????????????????????????????????????C.?2个???????????????????????????????????????D.?1个
二、填空题(共10题;共36分)
11.将二次函数y=2x2-1的图像沿y轴向上平移2个单位,所得图像对应的函数表达式为________.
12.抛物线y=ax2+bx﹣3经过点(1,1),则代数式a+b的值为________
13.已知y=
是关于x的二次函数,则a的值为________.
14.如图,是边长为1的正方形OABC绕顶点O顺时针旋转75°后得到的,原正方形的顶点A在x轴的正半轴上,此时点B恰好落在函数y=ax2(a<0)的图象上,则a的值为________.
15.已知抛物线y=ax2+bx经过点(﹣4,0),则这条抛物线的对称轴是________.
16.抛物线y=a(x+1)2经过点(﹣2,1),则a=________.
17.形如:y=ax2+bx+c(a≠0)的函数叫二次函数,它的图象是一条抛物线.类比一元一次方程的解可以看成两条直线的交点的横坐标;则一元二次方程x2+x﹣3=0的解可以看成抛物线y=x2+x﹣3与直线y=0(x轴)的交点的横坐标;也可以看成是抛物线y=x2与直线y=________
的交点的横坐标;也可以看成是抛物线y= ________?与直线y=﹣x的交点的横坐标;
18.抛物线y=﹣x2﹣2x+3与x轴交点为________,与y轴交点为________.
19.如图,已知抛物线y=x2+bx+c经过点(0,﹣3),请你确定一个b的值,使该抛物线与x轴的一个交点在(1,0)和(3,0)之间.你确定的b的值是________.
20.如图抛物线与x轴分别交于A、B两点,顶点C在y轴负半轴上,也在正方形ADEB的边上,已知正方形ADEB的边长为2,若正方形FGMN的顶点F、G落在x轴上,顶点M、N落在图中的抛物线上,则正方形FGMN的边长为________.
三、解答题(共8题;共54分)
21.如图,一块矩形草地的长为100m,宽为80m,欲在中间修筑两条互相垂直的宽为x(m)的小路,这时草坪的面积为y(m2).求y与x的函数关系式,并求出x的取值范围.
22.如图,在△ABC中,∠B=90°,AB=12,BC=24,动点P从点A开始沿边AB向终点B以每秒2个单位长度的速度移动,动点Q从点B开始沿边BC以每秒4个单位长度的速度向终点C移动,如果点P、Q分别从点A、B同时出发,那么△PBQ的面积S随出发时间t(s)如何变化?写出函数关系式及t的取值范围.
23.如图,用50m长的护栏全部用于建造一块靠墙的长方形花园,写出长方形花园的面积y(m2)与它与墙平行的边的长x(m)之间的函数.
24.在某市开展的环境创优活动中,某居民小区要在一块靠墙(墙长15米)的空地上修建一个矩形花园ABCD,花园的一边靠墙,另三边用总长为40m的栅栏围成,若设花园与墙平行的一边长为x(m),花园的面积为y(m2)。
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)满足条件的花园面积能达到200m2吗?若能,求出此时x的值,若不能,说明理由:
(3)根据(1)中求得的函数关系式,判断当x取何值时,花园的面积最大?最大面积是多少?
25.为鼓励大学毕业生自主创业,某市政府出台了相关政策:由政府协调,本市企业按成本价提供产品给大学毕业生自主销售,成本价与出厂价之间的差价由政府承担,李明按照相关政策投资销售本市生产的一种新型节能灯,已知这种节能灯的成本价为每件10元,出厂价为每件12元,每月销售量y(件)与销售单价x(元)之间的关系近似满足一次函数:y=-10x+500.
⑴李明在开始创业的第一个月将销售单价定为20元,那么政府这个月为他承担的总差价为多少元?
⑵设李明获得的利润为W(元),当销售单价定为多少元时,每月可获得最大利润?
⑶物价部门规定,这种节能灯的销售单价不得高于25元,如果李明想要每月获得的利润不低于3000元,那么政府为他承担的总差价最少为多少元?
26.在美化校园的活动中,某综合实践小组的同学借如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形的花圃ABCD(篱笆只围AB、BC两边)设AB=xm.
(1)若想围得花圃面积为192cm2
,
求x的值;
(2)若在点P处有一棵小树与墙CD、AD的距离分别为15m和6m,要将这棵树围在花圃内(含边界,不考虑树干的粗细),求花圃面积S的最大值.
27.(2017·金华)(本题8分)
甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分.
如图,甲
在O点正上方1m的P处发出一球,羽毛球飞行的高度y(m)与水平距离x(m)之间满足函数表达式
,已知点O与球网的水平距离为5m,球网的高度1.55m.
(1)当a=?
时,①求h的值.②通过计算判断此球能否过网.
(2)若甲发球过网后,羽毛球飞行到与点O的水平距离为7m,离地面的高度为
m的Q处时,乙扣球成功,求a的值.
28.如图,Rt△ABC中,∠C=90°,BC=6,AC=8.点P,Q都是斜边AB上的动点,点P从B
向A运动(不与点B重合),点Q从A向B运动,BP=AQ.点D,E分别是点A,B以Q,P为对称中心的对称点,
HQ⊥AB于Q,交AC于点H.当点E到达顶点A时,P,Q同时停止运动.设BP的长为x,△HDE的面积为y.
(1)求证:△DHQ∽△ABC;
(2)求y关于x的函数解析式并求y的最大值;
(3)当x为何值时,△HDE为等腰三角形?
答案解析部分
一、单选题
1.【答案】B
2.【答案】A
3.【答案】C
4.【答案】C
5.【答案】C
6.【答案】B
7.【答案】D
8.【答案】D
9.【答案】C
10.【答案】D
二、填空题
11.【答案】
12.【答案】4
13.【答案】?3
14.【答案】﹣
15.【答案】x=-2
16.【答案】1
17.【答案】﹣x+3;x2﹣3
18.【答案】(﹣3,0);(1,0);(0,3)
19.【答案】1(在﹣2<b<2范围内的任何一个数)
20.【答案】
三、解答题
21.【答案】解:设中间修筑两条互相垂直的宽为x(m)的小路,草坪的面积为y(m2),
根据题意得出:y=100﹣80﹣80x﹣100x+x2=x2﹣180x+8000(0<x<80)
22.【答案】解:△PBQ的面积S随出发时间t(s)成二次函数关系变化,
∵在△ABC中,∠B=90°,AB=12,BC=24,动点P从点A开始沿边AB向终点B以每秒2个单位长度的速度移动,
动点Q从点B开始沿边BC以每秒4个单位长度的速度向终点C移动,
∴BP=12﹣2t,BQ=4t,
∴△PBQ的面积S随出发时间t(s)的解析式为:y=
(12﹣2t)×4t=﹣4t2+24t,(0<t<6)
23.【答案】解:∵与墙平行的边的长为x(m),则垂直于墙的边长为:
?=(25﹣0.5x)m,
根据题意得出:y=x(25﹣0.5x)=﹣0.5x2+25x
24.【答案】解:(1)根据题意得:,
即y=﹣x2+20x(0<x≤15);
(2)当y=200时,即﹣x2+20x=200,
解得x1=x2=20>15,
∴花园面积不能达到200m2;
(3)∵y=﹣x2+20x的图象是开口向下的抛物线,对称轴为x=20,
∴当0<x≤15时,y随x的增大而增大.
∴x=15时,y有最大值,
y最大值=﹣×152+20×15=187.5m2
即当x=15时,花园的面积最大,最大面积为187.5m2
.
25.【答案】解:⑴当x=20时,y=-10x+500=-10×20+500=300,
300×(12-10)=300×2=600,
即政府这个月为他承担的总差价为600元.
⑵依题意得,W=(x-10)(-10x+500)=-10x2+600x-5000=-10(x-30)2+4000
∵a=-10<0,∴当x=30时,W有最大值4000.
即当销售单价定为30元时,每月可获得最大利润4000元.
⑶由题意得:-10x2+600x-5000=3000,解得:x1=20,x2=40.
∵a=-10<0,抛物线开口向下,
∴结合图象可知:当20≤x≤40时,W≥3000.
又∵x≤25,
∴当20≤x≤25时,W≥3000.
设政府每个月为他承担的总差价为p元,
∴p=(12-10)×(-10x+500)
=-20x+1000.
∵k=-20<0.
∴p随x的增大而减小,∴当x=25时,p有最小值500.
即销售单价定为25元时,政府每个月为他承担的总差价最少为500元.
26.【答案】(1)解:由题意得:x(28-x)=192,解此方程得x1=
12,x2=16
(2)解:花圃面积S=
x(28-x)=
-(x-14)2+196,
由题意知
,解得6≤x≤13,
在6≤x≤13的范围内,S随x增大而增大,
∴当x=13时,S最大值=-(13-14)2+196=195(m2).
27.【答案】(1)解:①∵a=?
,P(0,1);
∴1=
+h;
∴h=
;
②把x=5代入y=
得:
y==1.625;
∵1.625>1.55;
∴此球能过网.
(2)解:把(0,1),(7,
)代入y=a得:;
;解得:;
∴a=.
28.【答案】解:(1)∵A、D关于点Q成中心对称,HQ⊥AB,
∴HQD=C=90°,HD=HA,
∴HDQ=A,
∴△DHQ∽△ABC.
(2)①如图1,当0
此时y=(10-4x)x=-x2+x..
当x=时,最大值y=.
②如图2,当时,
ED=4x-10,QH=AQtanA=x,
此时y=(4x-10)x=x2-x..
当x=5时,最大值y=.
∴y与x之间的函数解析式为y=
y的最大值是.
(3)①如图1,当0
DE=10-4x,
∴10-4x=x,x=.
显然ED=EH,HD=HE不可能;
②如图2,当时,
若DE=DH,4x-10=x,x=;
若HD=HE,此时点D,E分别与点B,A重合,x=5;
若ED=EH,则△EDH∽△HDA,
∴,,x=.?
∴当x的值为,,5,,时,△HDE是等腰三角形
(
第
6
页
共
9
页
)
