冀教版九年级数学下册 第32章 投影与试图单元测试题(Word版 附答案)
文档属性
| 名称 | 冀教版九年级数学下册 第32章 投影与试图单元测试题(Word版 附答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-20 00:00:00 | ||
图片预览

文档简介
第三十二章 投影与试图
一、选择题(每小题4分,共32分)
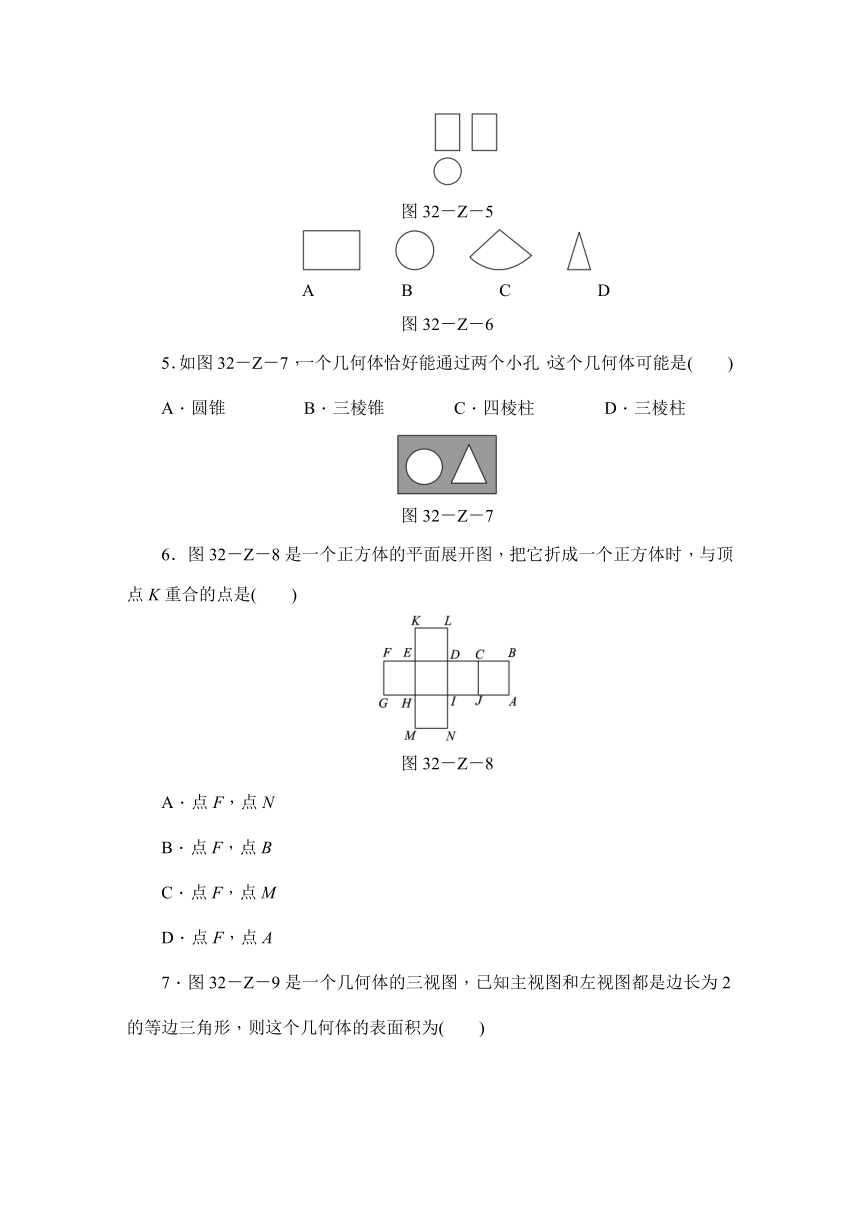
1.如图32-Z-1,晚上小亮在路灯下散步,他从A处背着路灯灯柱方向径直走到B处,这一过程中他在该路灯灯光下的影子( )
图32-Z-1
A.逐渐变短
B.逐渐变长
C.先变短后变长
D.先变长后变短
2.在一个晴朗的下午,小丽拿着一块矩形木板,在阳光下做投影试验,矩形木板在地面上形成的投影不可能是( )
图32-Z-2
3.如图32-Z-3,桌上放着一摞书和一个茶杯,则主视图是( )
A B C D
图32-Z-4
图32-Z-3
4.图32-Z-5是某几何体的三视图,则该几何体的侧面展开图是( )
图32-Z-5
A B C D
图32-Z-6
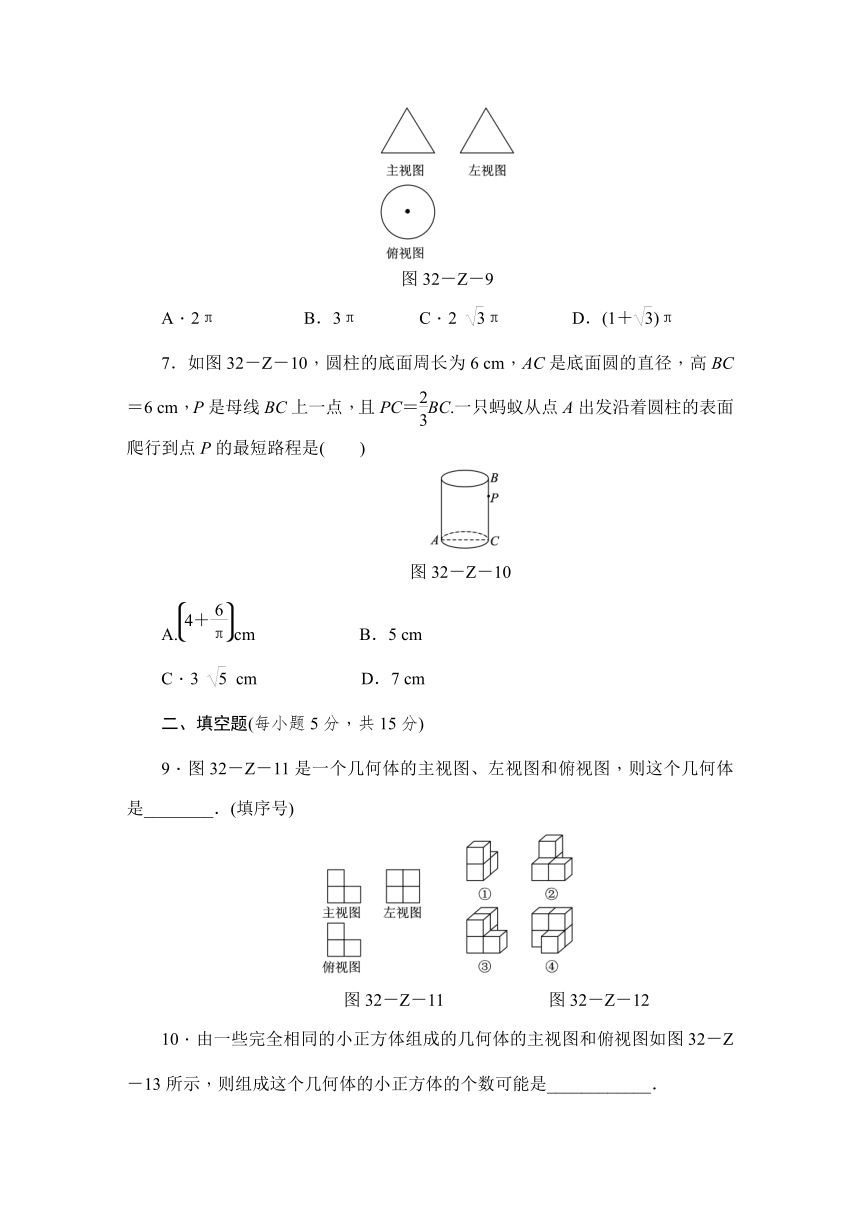
5.如图32-Z-7,一个几何体恰好能通过两个小孔,这个几何体可能是( )
A.圆锥
B.三棱锥
C.四棱柱
D.三棱柱
图32-Z-7
图32-Z-8是一个正方体的平面展开图,把它折成一个正方体时,与顶点K重合的点是( )
图32-Z-8
A.点F,点N
B.点F,点B
C.点F,点M
D.点F,点A
7.图32-Z-9是一个几何体的三视图,已知主视图和左视图都是边长为2的等边三角形,则这个几何体的表面积为( )
图32-Z-9
A.2π
B.3π
C.2
π
D.(1+)π
如图32-Z-10,圆柱的底面周长为6
cm,AC是底面圆的直径,高BC=6
cm,P是母线BC上一点,且PC=BC.一只蚂蚁从点A出发沿着圆柱的表面爬行到点P的最短路程是( )
图32-Z-10
A.cm
B.5
cm
C.3
cm
D.7
cm
二、填空题(每小题5分,共15分)
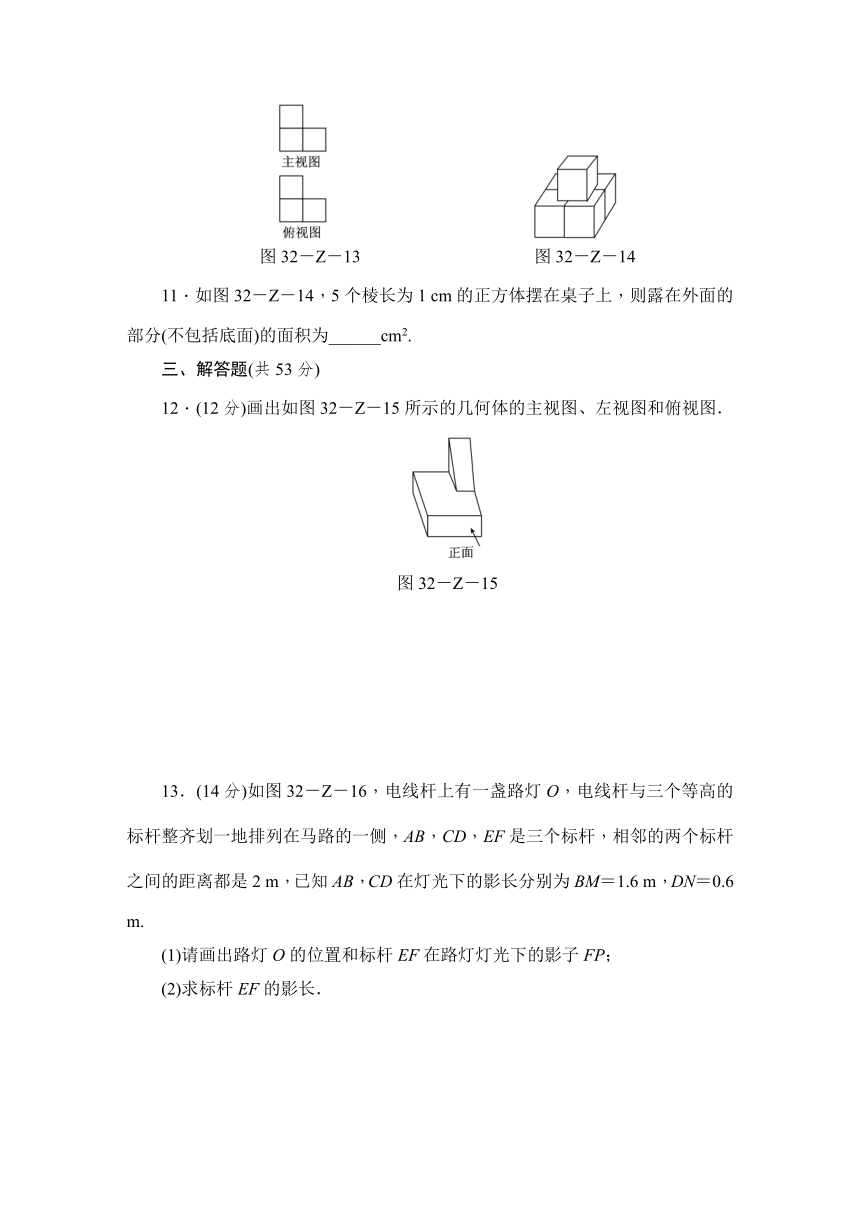
9.图32-Z-11是一个几何体的主视图、左视图和俯视图,则这个几何体是________.(填序号)
图32-Z-11 图32-Z-12
10.由一些完全相同的小正方体组成的几何体的主视图和俯视图如图32-Z-13所示,则组成这个几何体的小正方体的个数可能是____________.
图32-Z-13
图32-Z-14
11.如图32-Z-14,5个棱长为1
cm的正方体摆在桌子上,则露在外面的部分(不包括底面)的面积为______cm2.
三、解答题(共53分)
12.(12分)画出如图32-Z-15所示的几何体的主视图、左视图和俯视图.
图32-Z-15
13.(14分)如图32-Z-16,电线杆上有一盏路灯O,电线杆与三个等高的标杆整齐划一地排列在马路的一侧,AB,CD,EF是三个标杆,相邻的两个标杆之间的距离都是2
m,已知AB,CD在灯光下的影长分别为BM=1.6
m,DN=0.6
m.
(1)请画出路灯O的位置和标杆EF在路灯灯光下的影子FP;
(2)求标杆EF的影长.
图32-Z-16
14.(12分)图32-Z-17是一个几何体的三视图,其中俯视图是等边三角形.
(1)请写出这个几何体的名称;
(2)求这个几何体的表面积.
图32-Z-17
15.(15分)图32-Z-18①是一起吊重物的简单装置,AB是吊杆,当它倾斜时,将重物挂起,当它逐渐直立时,重物便能逐渐升高.在阳光下,当吊杆的倾斜角∠ABC=60°时,量得吊杆的影子长BC=11.5米,很快将吊杆直立(直立过程所需的时间忽略不计),如图32-Z-19②,AB与地面垂直时,量得吊杆AB的影长BC=4米,求吊杆AB的长.
图32-Z-18
教师详解详析
【作者说卷】
本章是初中数学知识的最后一章,学好本章知识可以解决生活中的许多与视图、投影有关的实际问题,同时为下一阶段的学习打下基础并做好准备.学习投影与视图的知识可以把生活中的平面图形,如简单的模型图、平面图、地图、照片等与数学知识联系和统一起来,用数学化的知识来描述形形色色的图形.
本套试题在考查学生基础知识、基本技能的同时,也考查了转化思想(空间问题平面化,曲折问题平直化,整体与局部)、数学建模思想、分类讨论思想等数学思想方法的运用.
1.B 2.A 3.A 4.A
5.A [解析]
俯视图为圆的几何体为球,圆锥,圆柱,再根据其他视图,可知此几何体为圆锥.故选A.
6.B [解析]
当把这个平面图形折成正方体时,与顶点K重合的点是F,B.故选B.
7.B
8.B [解析]
首先画出圆柱的侧面展开图,根据高BC=6
cm,PC=BC,求出PC=×6=4(cm),在Rt△ACP中,根据勾股定理求出AP的长.具体的解答过程如下:
侧面展开图如图所示,
∵圆柱的底面周长为6
cm,
∴AC=3
cm.
∵PC=BC,
∴PC=×6=4(cm).
在Rt△ACP中,AP2=AC2+PC2,
∴AP==5(cm).故选B.
9.③ [解析]
由俯视图可知,该几何体有2行2列,且第1列有2个正方体,第2列第1行有1个正方体,由主视图和左视图可知,第1列有2层,每层2个,第2列第1行有1个正方体.故答案为③.
10.4或5
11.16 [解析]
观察图形可知五个小正方体的表面积减去彼此重叠的10个面和底面的4个面的面积即为所求.
12.解:如图所示:
13.解:(1)如图:
(2)如图,连接AC,CE,则由题意可知A,C,E三点共线.设EF的影长FP=x
m,
可证==,
∴=,
解得x=0.4.
答:标杆EF的影长为0.4
m.
14.解:(1)这个几何体为三棱柱.
(2)这个几何体的表面积=3×3×+2××2×=
(cm2).
15.解:在题图①中,过点A作AD⊥BC于点D.
设BD=x米,则DC=(11.5-x)米.
又因为∠ABC=60°,
所以AD=x米,AB=2x米.
因为太阳光是平行的,根据同一时刻,同一地点物高与影长成正比,
所以题图①中的“AD∶DC”和题图②中的“AB∶BC”相等,
即x∶(11.5-x)=2x∶4,
解得x=11.5-2
(x=0不符合题意,舍去),
所以吊杆AB=2x=(23-4
)米.
一、选择题(每小题4分,共32分)
1.如图32-Z-1,晚上小亮在路灯下散步,他从A处背着路灯灯柱方向径直走到B处,这一过程中他在该路灯灯光下的影子( )
图32-Z-1
A.逐渐变短
B.逐渐变长
C.先变短后变长
D.先变长后变短
2.在一个晴朗的下午,小丽拿着一块矩形木板,在阳光下做投影试验,矩形木板在地面上形成的投影不可能是( )
图32-Z-2
3.如图32-Z-3,桌上放着一摞书和一个茶杯,则主视图是( )
A B C D
图32-Z-4
图32-Z-3
4.图32-Z-5是某几何体的三视图,则该几何体的侧面展开图是( )
图32-Z-5
A B C D
图32-Z-6
5.如图32-Z-7,一个几何体恰好能通过两个小孔,这个几何体可能是( )
A.圆锥
B.三棱锥
C.四棱柱
D.三棱柱
图32-Z-7
图32-Z-8是一个正方体的平面展开图,把它折成一个正方体时,与顶点K重合的点是( )
图32-Z-8
A.点F,点N
B.点F,点B
C.点F,点M
D.点F,点A
7.图32-Z-9是一个几何体的三视图,已知主视图和左视图都是边长为2的等边三角形,则这个几何体的表面积为( )
图32-Z-9
A.2π
B.3π
C.2
π
D.(1+)π
如图32-Z-10,圆柱的底面周长为6
cm,AC是底面圆的直径,高BC=6
cm,P是母线BC上一点,且PC=BC.一只蚂蚁从点A出发沿着圆柱的表面爬行到点P的最短路程是( )
图32-Z-10
A.cm
B.5
cm
C.3
cm
D.7
cm
二、填空题(每小题5分,共15分)
9.图32-Z-11是一个几何体的主视图、左视图和俯视图,则这个几何体是________.(填序号)
图32-Z-11 图32-Z-12
10.由一些完全相同的小正方体组成的几何体的主视图和俯视图如图32-Z-13所示,则组成这个几何体的小正方体的个数可能是____________.
图32-Z-13
图32-Z-14
11.如图32-Z-14,5个棱长为1
cm的正方体摆在桌子上,则露在外面的部分(不包括底面)的面积为______cm2.
三、解答题(共53分)
12.(12分)画出如图32-Z-15所示的几何体的主视图、左视图和俯视图.
图32-Z-15
13.(14分)如图32-Z-16,电线杆上有一盏路灯O,电线杆与三个等高的标杆整齐划一地排列在马路的一侧,AB,CD,EF是三个标杆,相邻的两个标杆之间的距离都是2
m,已知AB,CD在灯光下的影长分别为BM=1.6
m,DN=0.6
m.
(1)请画出路灯O的位置和标杆EF在路灯灯光下的影子FP;
(2)求标杆EF的影长.
图32-Z-16
14.(12分)图32-Z-17是一个几何体的三视图,其中俯视图是等边三角形.
(1)请写出这个几何体的名称;
(2)求这个几何体的表面积.
图32-Z-17
15.(15分)图32-Z-18①是一起吊重物的简单装置,AB是吊杆,当它倾斜时,将重物挂起,当它逐渐直立时,重物便能逐渐升高.在阳光下,当吊杆的倾斜角∠ABC=60°时,量得吊杆的影子长BC=11.5米,很快将吊杆直立(直立过程所需的时间忽略不计),如图32-Z-19②,AB与地面垂直时,量得吊杆AB的影长BC=4米,求吊杆AB的长.
图32-Z-18
教师详解详析
【作者说卷】
本章是初中数学知识的最后一章,学好本章知识可以解决生活中的许多与视图、投影有关的实际问题,同时为下一阶段的学习打下基础并做好准备.学习投影与视图的知识可以把生活中的平面图形,如简单的模型图、平面图、地图、照片等与数学知识联系和统一起来,用数学化的知识来描述形形色色的图形.
本套试题在考查学生基础知识、基本技能的同时,也考查了转化思想(空间问题平面化,曲折问题平直化,整体与局部)、数学建模思想、分类讨论思想等数学思想方法的运用.
1.B 2.A 3.A 4.A
5.A [解析]
俯视图为圆的几何体为球,圆锥,圆柱,再根据其他视图,可知此几何体为圆锥.故选A.
6.B [解析]
当把这个平面图形折成正方体时,与顶点K重合的点是F,B.故选B.
7.B
8.B [解析]
首先画出圆柱的侧面展开图,根据高BC=6
cm,PC=BC,求出PC=×6=4(cm),在Rt△ACP中,根据勾股定理求出AP的长.具体的解答过程如下:
侧面展开图如图所示,
∵圆柱的底面周长为6
cm,
∴AC=3
cm.
∵PC=BC,
∴PC=×6=4(cm).
在Rt△ACP中,AP2=AC2+PC2,
∴AP==5(cm).故选B.
9.③ [解析]
由俯视图可知,该几何体有2行2列,且第1列有2个正方体,第2列第1行有1个正方体,由主视图和左视图可知,第1列有2层,每层2个,第2列第1行有1个正方体.故答案为③.
10.4或5
11.16 [解析]
观察图形可知五个小正方体的表面积减去彼此重叠的10个面和底面的4个面的面积即为所求.
12.解:如图所示:
13.解:(1)如图:
(2)如图,连接AC,CE,则由题意可知A,C,E三点共线.设EF的影长FP=x
m,
可证==,
∴=,
解得x=0.4.
答:标杆EF的影长为0.4
m.
14.解:(1)这个几何体为三棱柱.
(2)这个几何体的表面积=3×3×+2××2×=
(cm2).
15.解:在题图①中,过点A作AD⊥BC于点D.
设BD=x米,则DC=(11.5-x)米.
又因为∠ABC=60°,
所以AD=x米,AB=2x米.
因为太阳光是平行的,根据同一时刻,同一地点物高与影长成正比,
所以题图①中的“AD∶DC”和题图②中的“AB∶BC”相等,
即x∶(11.5-x)=2x∶4,
解得x=11.5-2
(x=0不符合题意,舍去),
所以吊杆AB=2x=(23-4
)米.
