北师大版八年级下册第一章1.1.1等腰三角形(第一课时)课件(18张)
文档属性
| 名称 | 北师大版八年级下册第一章1.1.1等腰三角形(第一课时)课件(18张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-20 00:00:00 | ||
图片预览





文档简介
北师大版八年级(下)
1.1等腰三角形
第一章 三角形的证明
第1课时 三角形全等和等腰三角形的性质
学习目标
1.进一步了解“8条基本事实”,学会证明的基本步骤和书写格式.
2.能证明:“AAS”这一全等的判定定理,能利用全等三角形的性质去证明等腰三角形的有关性质定理及其推论.
3.灵活运用等腰三角形的性质进行计算和证明.
课前复习
1.两点确定一条直线.
2.两点之间线段最短.
3.同一平面内,过一点有且只有一条直线与已知直线垂直.
4.两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
5.过直线外一点有且只有一条直线与这条直线平行 .
6.两边及其夹角分别相等的两个三角形全等(SAS).
7.两角及其夹边分别相等的两个三角形全等(ASA).
8.三边对应相等的两个三角形全等(SSS).
那些年已有的事实(公理),你还记得她们吗?
再回首
想一想:在探索三角形全等的条件时,我们已经探索过“两角分别对应相等且其中一组等角的对边相等的两个三角形全等”这一结论,你能用已有的基本事实和定理证明这一结论吗?
聪明如我的你们
一定可以搞定哦!
画图试试!
注意对于一个命题的证明,需要哪三部曲哦?
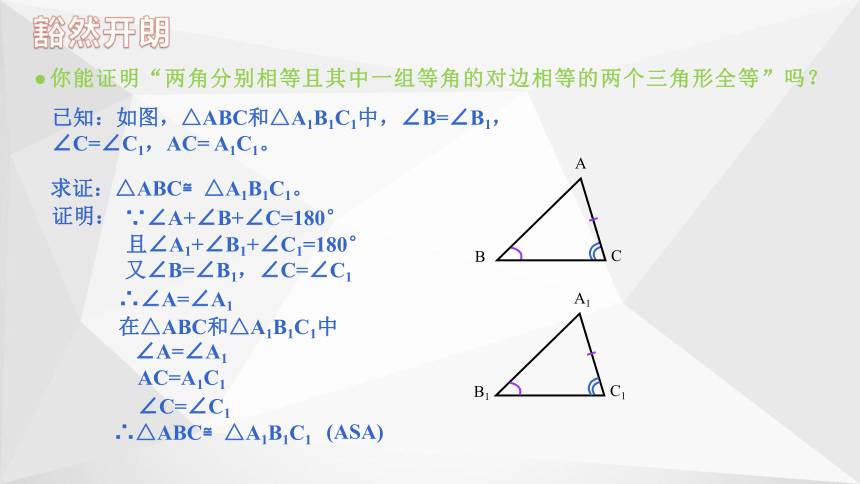
豁然开朗
你能证明“两角分别相等且其中一组等角的对边相等的两个三角形全等”吗?
A
B
C
A1
B1
C1
已知:如图,△ABC和△A1B1C1中,∠B=∠B1,
∠C=∠C1,AC= A1C1。
求证:△ABC≌△A1B1C1。
证明:
∵∠A+∠B+∠C=180°
且∠A1+∠B1+∠C1=180°
又∠B=∠B1,∠C=∠C1
∴∠A=∠A1
在△ABC和△A1B1C1中
∠A=∠A1
AC=A1C1
∠C=∠C1
∴△ABC≌△A1B1C1
(ASA)
新知诞生
定理:
两角分别相等且其中一组等角的对边相等的
两个三角形全等.
别忘老朋友
全等三角形对应边相等,对应角相等.
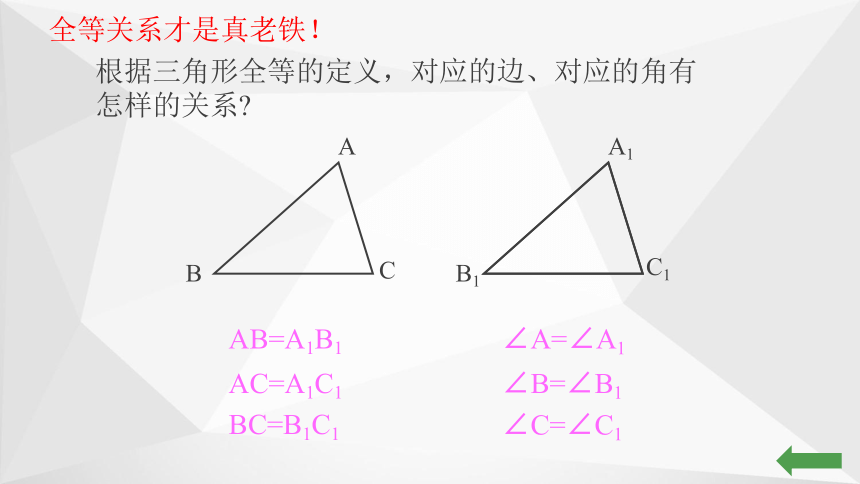
全等关系才是真老铁!
根据三角形全等的定义,对应的边、对应的角有怎样的关系?
A
B
C
A1
B1
C1
AB=A1B1
AC=A1C1
BC=B1C1
∠A=∠A1
∠B=∠B1
∠C=∠C1
她是谁?
你了解她多少?
你能证明吗?
知多少?
等腰三角形
两腰相等,两底角相等,“三线合一”
A
B
C
忆当年!
曾经的我们
将一个等腰三角形
按如图所示的方式
折叠,从而得出:
等腰三角形的
两个底角相等
新知探究
现在的我们
我要证明:
等腰三角形两个底角相等
A
B
C
新知探究
现在的我们
我要证明:
等腰三角形两个底角相等
A
B
C
已知:如图,在△ABC中,AB=AC.
求证:∠B=∠C.
证明:
新知探究
已知:如图,在△ABC中,AB=AC.
求证:∠B=∠C.
证明:
取BC的中点D,连接AD.
∴BD=CD
在△ABD和△ACD中:
AB=AC
BD=CD
AD=AD
∴△ABD≌△ACD
∴ ∠B=∠C
(SSS)
A
B
C
D
定理:
等腰三角形两个底角相等
简称:等边对等角
再想想
A
B
C
D
中线
AD还可以看作△ABC
的什么特殊线段吗?
AD是底边中线
AD是底边高线
AD是顶角平分线
推论:等腰三角形顶角平分线、底边上的中线及底边上的高线互相重合.
大名鼎鼎的“三线合一”哦!
——SSS
——HL
——SAS
1.一般的全等三角形的判定方法共有四种,分别是_______,
_______,_______,________.?
2.全等三角形的性质:全等三角形的对应边_____,对应角_____.?
3.等腰三角形的性质:
SSS
SAS
ASA
AAS
相等
相等
新知归纳
(1)等边对等角;
(2)“三线合一”.
1.在△ABC中,AB=AC.
(1)若∠A=40°,则∠C等于多少度?
(2)若∠B=72°,则∠A等于多少度?
变式练习:在等腰三角形ABC中,
(1)若∠A=40°,则∠C等于多少度?
(2)若∠A=100°,则∠C等于多少度?
2.如图,在△ABD中,C是BD边上的一点,且AC⊥BD,AC=BC=CD.
(1)求证:△ABD是等腰三角形;
(2)求∠BAD的度数.
A
B
C
D
1.教材习题1.1
2.对应练习册
课后练习
等腰三角形的故事……
欲知后事如何,请听下回分解!
1.1等腰三角形
第一章 三角形的证明
第1课时 三角形全等和等腰三角形的性质
学习目标
1.进一步了解“8条基本事实”,学会证明的基本步骤和书写格式.
2.能证明:“AAS”这一全等的判定定理,能利用全等三角形的性质去证明等腰三角形的有关性质定理及其推论.
3.灵活运用等腰三角形的性质进行计算和证明.
课前复习
1.两点确定一条直线.
2.两点之间线段最短.
3.同一平面内,过一点有且只有一条直线与已知直线垂直.
4.两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
5.过直线外一点有且只有一条直线与这条直线平行 .
6.两边及其夹角分别相等的两个三角形全等(SAS).
7.两角及其夹边分别相等的两个三角形全等(ASA).
8.三边对应相等的两个三角形全等(SSS).
那些年已有的事实(公理),你还记得她们吗?
再回首
想一想:在探索三角形全等的条件时,我们已经探索过“两角分别对应相等且其中一组等角的对边相等的两个三角形全等”这一结论,你能用已有的基本事实和定理证明这一结论吗?
聪明如我的你们
一定可以搞定哦!
画图试试!
注意对于一个命题的证明,需要哪三部曲哦?
豁然开朗
你能证明“两角分别相等且其中一组等角的对边相等的两个三角形全等”吗?
A
B
C
A1
B1
C1
已知:如图,△ABC和△A1B1C1中,∠B=∠B1,
∠C=∠C1,AC= A1C1。
求证:△ABC≌△A1B1C1。
证明:
∵∠A+∠B+∠C=180°
且∠A1+∠B1+∠C1=180°
又∠B=∠B1,∠C=∠C1
∴∠A=∠A1
在△ABC和△A1B1C1中
∠A=∠A1
AC=A1C1
∠C=∠C1
∴△ABC≌△A1B1C1
(ASA)
新知诞生
定理:
两角分别相等且其中一组等角的对边相等的
两个三角形全等.
别忘老朋友
全等三角形对应边相等,对应角相等.
全等关系才是真老铁!
根据三角形全等的定义,对应的边、对应的角有怎样的关系?
A
B
C
A1
B1
C1
AB=A1B1
AC=A1C1
BC=B1C1
∠A=∠A1
∠B=∠B1
∠C=∠C1
她是谁?
你了解她多少?
你能证明吗?
知多少?
等腰三角形
两腰相等,两底角相等,“三线合一”
A
B
C
忆当年!
曾经的我们
将一个等腰三角形
按如图所示的方式
折叠,从而得出:
等腰三角形的
两个底角相等
新知探究
现在的我们
我要证明:
等腰三角形两个底角相等
A
B
C
新知探究
现在的我们
我要证明:
等腰三角形两个底角相等
A
B
C
已知:如图,在△ABC中,AB=AC.
求证:∠B=∠C.
证明:
新知探究
已知:如图,在△ABC中,AB=AC.
求证:∠B=∠C.
证明:
取BC的中点D,连接AD.
∴BD=CD
在△ABD和△ACD中:
AB=AC
BD=CD
AD=AD
∴△ABD≌△ACD
∴ ∠B=∠C
(SSS)
A
B
C
D
定理:
等腰三角形两个底角相等
简称:等边对等角
再想想
A
B
C
D
中线
AD还可以看作△ABC
的什么特殊线段吗?
AD是底边中线
AD是底边高线
AD是顶角平分线
推论:等腰三角形顶角平分线、底边上的中线及底边上的高线互相重合.
大名鼎鼎的“三线合一”哦!
——SSS
——HL
——SAS
1.一般的全等三角形的判定方法共有四种,分别是_______,
_______,_______,________.?
2.全等三角形的性质:全等三角形的对应边_____,对应角_____.?
3.等腰三角形的性质:
SSS
SAS
ASA
AAS
相等
相等
新知归纳
(1)等边对等角;
(2)“三线合一”.
1.在△ABC中,AB=AC.
(1)若∠A=40°,则∠C等于多少度?
(2)若∠B=72°,则∠A等于多少度?
变式练习:在等腰三角形ABC中,
(1)若∠A=40°,则∠C等于多少度?
(2)若∠A=100°,则∠C等于多少度?
2.如图,在△ABD中,C是BD边上的一点,且AC⊥BD,AC=BC=CD.
(1)求证:△ABD是等腰三角形;
(2)求∠BAD的度数.
A
B
C
D
1.教材习题1.1
2.对应练习册
课后练习
等腰三角形的故事……
欲知后事如何,请听下回分解!
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
