北师大版九年级上册第二章2.6一元二次方程应用利润问题课件(25张)
文档属性
| 名称 | 北师大版九年级上册第二章2.6一元二次方程应用利润问题课件(25张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 15.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-20 00:00:00 | ||
图片预览






文档简介
一元二次方程的应用
利润问题
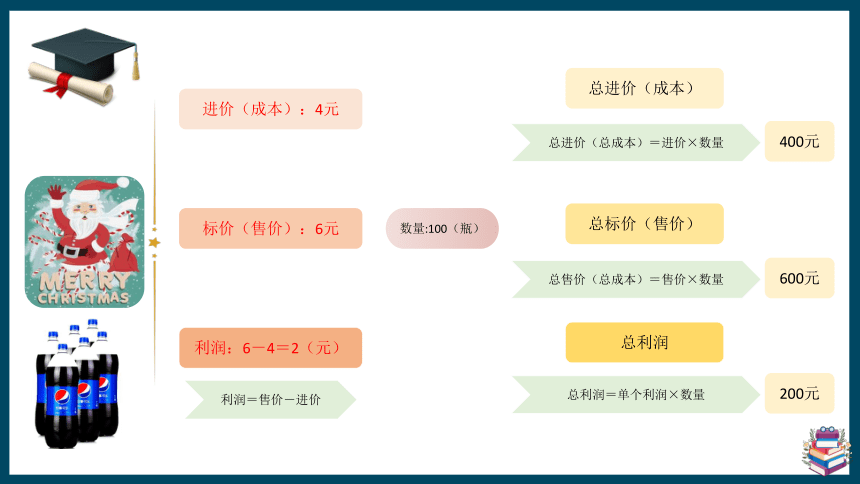
进价(成本):4元
标价(售价):6元
利润:6-4=2(元)
数量:100(瓶)
总进价(成本)
总标价(售价)
总利润
400元
总进价(总成本)=进价×数量
600元
总售价(总成本)=售价×数量
200元
总利润=单个利润×数量
利润=售价-进价
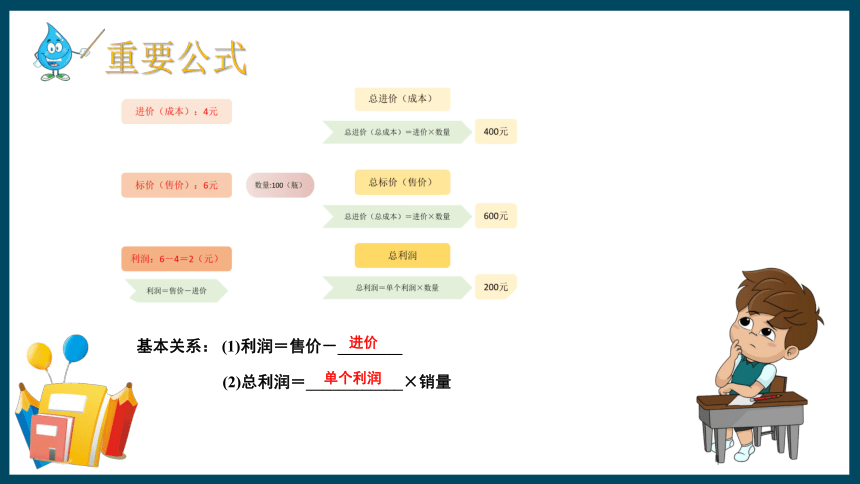
重要公式
基本关系: (1)利润=售价-________
(2)总利润=____________×销量
进价
单个利润
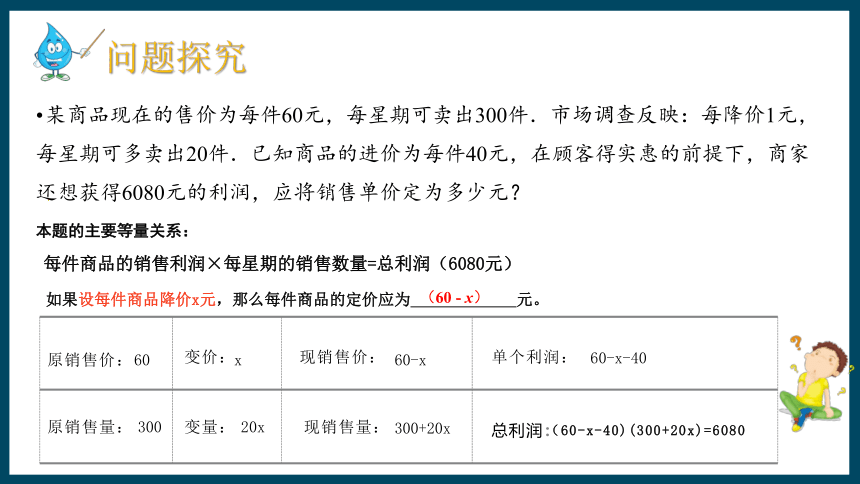
问题探究
某商品现在的售价为每件60元,每星期可卖出300件.市场调查反映:每降价1元,每星期可多卖出20件.已知商品的进价为每件40元,在顾客得实惠的前提下,商家还想获得6080元的利润,应将销售单价定为多少元?
本题的主要等量关系:
每件商品的销售利润×每星期的销售数量=总利润(6080元)
如果设每件商品降价x元,那么每件商品的定价应为 元。?
(60 - x)
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
原销售价:
原销售量:
现销售量:
变价:
x
变量:
20x
60
300
现销售价:
60-x
300+20x
总利润:
单个利润:
(60-x-40)(300+20x)=6080
60-x-40
解:设每件商品降价x元,那么每件商品的定价应(60-x)元,根据题意,得
整理,得: x?-5x+4=0
(x-1)(x-4)=0
解方程,得: x1 = 1,x2 = 4.
∴为使顾客实惠,取x=4时,定价为60-4=56
答:应将销售单价定为56元
(60-x-40)(300+20x)=6080
变式探究(一)
甲商品的进价为每件20元,商场确定其售价为每件40元. 经调查,该商品每降价0.2元,即可多销售10件.已知甲商品售价40元时每月可销售500件,若该商场希望该商品每月能盈利10000元,且尽可能扩大销售量,则该商品在原售价的基础上应如何调整?
本题的主要等量关系:
每件商品的销售利润×每星期的销售数量=总利润(6080元)
如果设每件商品降价x元,那么每件商品的定价应为 元。?
(60 - x)
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
原销售价:
原销售量:
现销售量:
变价:
x
变量:
60
300
现销售价:
60-x
总利润:
单个利润:
60-x-40
解:设每件商品降价x元,那么每件商品的定价应(60-x)元,根据题意,得
整理,得: x?-10x-200=0
(x-10)(x+20)=0
解方程,得: x1 = 10,x2 = ﹣20.
∴为使顾客实惠,取x=10时,定价为60-10=50
答:应将销售单价定为50元
新华商场销售某种冰箱,每台进价为2500元.市场调研表明:当销售价为2900元时,平均每天
能售出8台;而当销价每降低50元时,平均每天能多售4台.商场要想使这种冰箱的销售利润
平均每天达到5000元,每台冰箱的定价应为多少元?
如果设每台冰箱降价x元,那么每台冰箱的定价应为 元。?
(2900-x)
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
原销售价:
原销售量:
现销售量:
变价:
x
变量:
2900
8
现销售价:
2900-x
总利润:
单个利润:
2900-x-2500
同步练习
解:设每台冰箱降价x元,那么每台冰箱的定价应(2900-x)元,根据题意,得
整理,得: 整理,得:x2 - 300x + 22500 = 0.
解方程,得:
x1 = x2 = 150.
∴ 2900 - x = 2900 - 150 = 2750.
答:每台冰箱的定价应为2750元.
变式探究(二)
某商品现在的售价为每件60元,每星期可卖出300件.市场调查反映:每涨价1元,每星期可少卖出20件.已知商品的进价为每件40元,在顾客得实惠的前提下,商家还想获得5880元的利润,应将销售单价定为多少元?
本题的主要等量关系:
每件商品的销售利润×每星期的销售数量=总利润(5880元)
如果设每件商品涨价x元,那么每件商品的定价应为 元。?
(60+ x)
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
原销售价:
原销售量:
现销售量:
变价:
x
变量:
20x
60
300
现销售价:
60+x
300-20x
总利润:
单个利润:60+x-40
(60+x-40)(300-20x)=5880
解:设每件商品涨价x元,那么每件商品的定价应(60+x)元,根据题意,得
整理,得: x?+5x-6=0
(x-1)(x+6)=0
解方程,得: x1 = 1,x2 =-6.
∴为使顾客实惠,取x=1时,定价为60-1=59
答:应将销售单价定为59元
(60+x-40)(300-20x)=5880
变式探究(三)
某商品现在的售价为每件60元,每星期可卖出300件.市场调查反映:每涨价2元,每星期少卖出20件.已知商品的进价为每件40元,在顾客得实惠的前提下,商家还想获得4000元的利润,应将销售单价定为多少元?
本题的主要等量关系:
每件商品的销售利润×每星期的销售数量=总利润(6080元)
如果设每件商品涨价x元,那么每件商品的定价应为 元。?
(60 +x)
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
原销售价:
原销售量:
现销售量:
变价:
x
变量:
60
300
现销售价:
60+x
总利润:
单个利润:
2
60+x-40
解:设每件商品涨价x元,那么每件商品的定价应(60+x)元,根据题意,得
整理,得: x?-10x+200=0
(x-10)(x+20)=0
解方程,得: x1 = 10,x2 = ﹣20.
∴为使顾客实惠,取x=10时,定价为60-10=50
答:应将销售单价定为50元
问题2 要组织一次排球邀请赛,参赛的每两个队之间都要比赛一场.根据场地和时间等条件,赛程计划安排7天,每天安排4场比赛,比赛组织者应邀请多少个队参赛?
分析:全部比赛的场数为28场,
设应邀请x个队参赛,每个队要与其他(x-1)个队各赛1场,
所以全部比赛共????(?????1)2?场.
?
列方程 ????(?????1)2= 28. 化简整理得x2-x-56=0. ②
?
探究新知
观察方程① ② ,我们发现他们都不是一元一次方程,
那他们有什么共同点?
x2-75x+350=0 ①
共同点:(1)都是整式方程
(2)只含有一个未知数
(3)未知数的最高次都是二次
x2-x-56=0 ②
探究新知
像这样等式两边都是整式,只含有一个未知数(一元),并且未知数的最高次是2(二次)的方程,叫做一元二次方程。
一元二次方程的一般形式
一般地,任何一个关于x的一元二次方程,经过整理,都能化成
ax2+bx +c=0(a≠0).这种形式叫做一元二次方程的一般形式.
其中ax2是二次项,a是二次项系数;bx是一次项,b是一次项系数;c是常数项.
一元二次方程定义
新知讲解
发现:只有当a≠0时,未知数的最高次才是2次,满足一元二次方程的定义。b,c可以为任意实数。
当a≠0,c=0时 ax?+bx=0
当a≠0,b=0,c=0时 ax?=0
当a=0时 bx+c=0
当a≠0,b=0时 ax?+c=0
分析:
思考:为什么一般形式中限制a≠0?那么b、c可以为零吗?
考点精讲
利用一元二次方程定义判断方程类型
方法总结:
判断一个方程是不是一元二次方程,我们需要先将方程整理成
ax2+bx+c=0(a≠0)的形式,再看是否满足以下三个条件:
(1)是整式方程;(2)只含有一个未知数;(3)未知数的最高次数是2.
例1 下列方程一定是一元二次方程的是( )
A.3x? + 2x?-1=0 B.5x?-6y-3=0
?
C.ax?-x+2=0 D.3x?-2x-1=0
含有
分式
含有两个未知数
a可能
为0
D
考点精讲
利用一元二次方程定义求解未知数的值或取值范围
例2 已知:方程(m-3)????|?????1|-mx+1=0是关于x的一元二次方程,则m的值为( )
A.m=±3 B.m=3 C.m=3或m=﹣1 D.m=﹣1
?
D
【解析】根据一元二次方程的定义可知,要求最高次是二次的,并且二次项的系数不为0,则可以列出相关字母的方程.
解:依题意得:|m-1|=2且m-3≠0.解得m=-1.故选:D.
方法总结:
根据最高次是2的限定条件,列出关于未知数的方程。
最终排除二次项系数为0的未知数的值
同步练习
习题2 已知关于x的方程(m+2)????|????|+2x-1=0.求:
?
(1)当m为何值时是一元一次方程;
(2)当m 为何值时是一元二次方程。
解析:(1)由题意得:① 当m+2=0时,原方程是一元一次方程;
②当| m | =1时,原方程是一元一次方程.
综合解得:当m=-2或±1时,原方程是一元一次方程。
(2)由题意得:当m+2≠0,丨m丨=2时,原方程是一元二次
方程。解得m=2
考点精讲
一元二次方程的一般式及系数
例3 一元二次方程3x2﹣5= 4x的二次项系数、一次项系数、常数项分别是( )
A.3,﹣4,﹣5 B.3,﹣4,5
C.3,4,5 D.3,4,﹣5
D
【解析】先将方程通过移项变成一元二次方程的一般形式,得一元二次方程3x2﹣4x﹣5=0的二次项系数、一次项系数、常数项分别是3,﹣4,﹣5.
方法总结:要确定一元二次方程的各项系数,需要先将方程整理成一般形式,确定方程中的每一项,再确定各项系数。
同步练习
习题3 判断关于x方程x?-mx(2x-m+1)=x是不是一元二次方程,如果是,指出二次项系数及常数项.
解析:将原方程整理成一般形式得:(1-2m)x?+(m?-m-1)x=0,
当1-2m≠0,即m≠12时,原方程是一元二次方程,
二次项系数为:1-2m;常数项为0.
?
知识小结
1、一元二次方程的定义:
只含有一个未知数(一元),并且未知数的最高次为2(二次)的整式方程,叫做一元二次方程.
2、一元二次方程的一般形式及各项系数:
一般形式是ax2+bx +c=0(a≠0).其中ax2是二次项,a是二次项系数;bx是一次项,b是一次项系数;c是常数项.
课后练习
4.若方程(a-1)xa?+1+5x=4是一元二次方程,求a的值。
1.关于x的方程mx?-3x= x?-mx+2是一元二次方程,则m的取值范是 .
3.已知关于x的方程(m?-4)x?+(m-2)x+3m-1=0,
当m______时,该方程是一元二次方程;
当m=____时,该方程是一元一次方程。
2.如图,在宽为20m,长30m的矩形场地上,修筑同样宽的
两条道路,余下的部分作为耕地,要使耕地的面积为500m2,
若设路宽为x米,则可列方程为:_____________,它的一般
形式是____________,其中的二次项系数是_____,一次项
是 ,常数项是_________。
利润问题
进价(成本):4元
标价(售价):6元
利润:6-4=2(元)
数量:100(瓶)
总进价(成本)
总标价(售价)
总利润
400元
总进价(总成本)=进价×数量
600元
总售价(总成本)=售价×数量
200元
总利润=单个利润×数量
利润=售价-进价
重要公式
基本关系: (1)利润=售价-________
(2)总利润=____________×销量
进价
单个利润
问题探究
某商品现在的售价为每件60元,每星期可卖出300件.市场调查反映:每降价1元,每星期可多卖出20件.已知商品的进价为每件40元,在顾客得实惠的前提下,商家还想获得6080元的利润,应将销售单价定为多少元?
本题的主要等量关系:
每件商品的销售利润×每星期的销售数量=总利润(6080元)
如果设每件商品降价x元,那么每件商品的定价应为 元。?
(60 - x)
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
原销售价:
原销售量:
现销售量:
变价:
x
变量:
20x
60
300
现销售价:
60-x
300+20x
总利润:
单个利润:
(60-x-40)(300+20x)=6080
60-x-40
解:设每件商品降价x元,那么每件商品的定价应(60-x)元,根据题意,得
整理,得: x?-5x+4=0
(x-1)(x-4)=0
解方程,得: x1 = 1,x2 = 4.
∴为使顾客实惠,取x=4时,定价为60-4=56
答:应将销售单价定为56元
(60-x-40)(300+20x)=6080
变式探究(一)
甲商品的进价为每件20元,商场确定其售价为每件40元. 经调查,该商品每降价0.2元,即可多销售10件.已知甲商品售价40元时每月可销售500件,若该商场希望该商品每月能盈利10000元,且尽可能扩大销售量,则该商品在原售价的基础上应如何调整?
本题的主要等量关系:
每件商品的销售利润×每星期的销售数量=总利润(6080元)
如果设每件商品降价x元,那么每件商品的定价应为 元。?
(60 - x)
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
原销售价:
原销售量:
现销售量:
变价:
x
变量:
60
300
现销售价:
60-x
总利润:
单个利润:
60-x-40
解:设每件商品降价x元,那么每件商品的定价应(60-x)元,根据题意,得
整理,得: x?-10x-200=0
(x-10)(x+20)=0
解方程,得: x1 = 10,x2 = ﹣20.
∴为使顾客实惠,取x=10时,定价为60-10=50
答:应将销售单价定为50元
新华商场销售某种冰箱,每台进价为2500元.市场调研表明:当销售价为2900元时,平均每天
能售出8台;而当销价每降低50元时,平均每天能多售4台.商场要想使这种冰箱的销售利润
平均每天达到5000元,每台冰箱的定价应为多少元?
如果设每台冰箱降价x元,那么每台冰箱的定价应为 元。?
(2900-x)
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
原销售价:
原销售量:
现销售量:
变价:
x
变量:
2900
8
现销售价:
2900-x
总利润:
单个利润:
2900-x-2500
同步练习
解:设每台冰箱降价x元,那么每台冰箱的定价应(2900-x)元,根据题意,得
整理,得: 整理,得:x2 - 300x + 22500 = 0.
解方程,得:
x1 = x2 = 150.
∴ 2900 - x = 2900 - 150 = 2750.
答:每台冰箱的定价应为2750元.
变式探究(二)
某商品现在的售价为每件60元,每星期可卖出300件.市场调查反映:每涨价1元,每星期可少卖出20件.已知商品的进价为每件40元,在顾客得实惠的前提下,商家还想获得5880元的利润,应将销售单价定为多少元?
本题的主要等量关系:
每件商品的销售利润×每星期的销售数量=总利润(5880元)
如果设每件商品涨价x元,那么每件商品的定价应为 元。?
(60+ x)
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
原销售价:
原销售量:
现销售量:
变价:
x
变量:
20x
60
300
现销售价:
60+x
300-20x
总利润:
单个利润:60+x-40
(60+x-40)(300-20x)=5880
解:设每件商品涨价x元,那么每件商品的定价应(60+x)元,根据题意,得
整理,得: x?+5x-6=0
(x-1)(x+6)=0
解方程,得: x1 = 1,x2 =-6.
∴为使顾客实惠,取x=1时,定价为60-1=59
答:应将销售单价定为59元
(60+x-40)(300-20x)=5880
变式探究(三)
某商品现在的售价为每件60元,每星期可卖出300件.市场调查反映:每涨价2元,每星期少卖出20件.已知商品的进价为每件40元,在顾客得实惠的前提下,商家还想获得4000元的利润,应将销售单价定为多少元?
本题的主要等量关系:
每件商品的销售利润×每星期的销售数量=总利润(6080元)
如果设每件商品涨价x元,那么每件商品的定价应为 元。?
(60 +x)
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
原销售价:
原销售量:
现销售量:
变价:
x
变量:
60
300
现销售价:
60+x
总利润:
单个利润:
2
60+x-40
解:设每件商品涨价x元,那么每件商品的定价应(60+x)元,根据题意,得
整理,得: x?-10x+200=0
(x-10)(x+20)=0
解方程,得: x1 = 10,x2 = ﹣20.
∴为使顾客实惠,取x=10时,定价为60-10=50
答:应将销售单价定为50元
问题2 要组织一次排球邀请赛,参赛的每两个队之间都要比赛一场.根据场地和时间等条件,赛程计划安排7天,每天安排4场比赛,比赛组织者应邀请多少个队参赛?
分析:全部比赛的场数为28场,
设应邀请x个队参赛,每个队要与其他(x-1)个队各赛1场,
所以全部比赛共????(?????1)2?场.
?
列方程 ????(?????1)2= 28. 化简整理得x2-x-56=0. ②
?
探究新知
观察方程① ② ,我们发现他们都不是一元一次方程,
那他们有什么共同点?
x2-75x+350=0 ①
共同点:(1)都是整式方程
(2)只含有一个未知数
(3)未知数的最高次都是二次
x2-x-56=0 ②
探究新知
像这样等式两边都是整式,只含有一个未知数(一元),并且未知数的最高次是2(二次)的方程,叫做一元二次方程。
一元二次方程的一般形式
一般地,任何一个关于x的一元二次方程,经过整理,都能化成
ax2+bx +c=0(a≠0).这种形式叫做一元二次方程的一般形式.
其中ax2是二次项,a是二次项系数;bx是一次项,b是一次项系数;c是常数项.
一元二次方程定义
新知讲解
发现:只有当a≠0时,未知数的最高次才是2次,满足一元二次方程的定义。b,c可以为任意实数。
当a≠0,c=0时 ax?+bx=0
当a≠0,b=0,c=0时 ax?=0
当a=0时 bx+c=0
当a≠0,b=0时 ax?+c=0
分析:
思考:为什么一般形式中限制a≠0?那么b、c可以为零吗?
考点精讲
利用一元二次方程定义判断方程类型
方法总结:
判断一个方程是不是一元二次方程,我们需要先将方程整理成
ax2+bx+c=0(a≠0)的形式,再看是否满足以下三个条件:
(1)是整式方程;(2)只含有一个未知数;(3)未知数的最高次数是2.
例1 下列方程一定是一元二次方程的是( )
A.3x? + 2x?-1=0 B.5x?-6y-3=0
?
C.ax?-x+2=0 D.3x?-2x-1=0
含有
分式
含有两个未知数
a可能
为0
D
考点精讲
利用一元二次方程定义求解未知数的值或取值范围
例2 已知:方程(m-3)????|?????1|-mx+1=0是关于x的一元二次方程,则m的值为( )
A.m=±3 B.m=3 C.m=3或m=﹣1 D.m=﹣1
?
D
【解析】根据一元二次方程的定义可知,要求最高次是二次的,并且二次项的系数不为0,则可以列出相关字母的方程.
解:依题意得:|m-1|=2且m-3≠0.解得m=-1.故选:D.
方法总结:
根据最高次是2的限定条件,列出关于未知数的方程。
最终排除二次项系数为0的未知数的值
同步练习
习题2 已知关于x的方程(m+2)????|????|+2x-1=0.求:
?
(1)当m为何值时是一元一次方程;
(2)当m 为何值时是一元二次方程。
解析:(1)由题意得:① 当m+2=0时,原方程是一元一次方程;
②当| m | =1时,原方程是一元一次方程.
综合解得:当m=-2或±1时,原方程是一元一次方程。
(2)由题意得:当m+2≠0,丨m丨=2时,原方程是一元二次
方程。解得m=2
考点精讲
一元二次方程的一般式及系数
例3 一元二次方程3x2﹣5= 4x的二次项系数、一次项系数、常数项分别是( )
A.3,﹣4,﹣5 B.3,﹣4,5
C.3,4,5 D.3,4,﹣5
D
【解析】先将方程通过移项变成一元二次方程的一般形式,得一元二次方程3x2﹣4x﹣5=0的二次项系数、一次项系数、常数项分别是3,﹣4,﹣5.
方法总结:要确定一元二次方程的各项系数,需要先将方程整理成一般形式,确定方程中的每一项,再确定各项系数。
同步练习
习题3 判断关于x方程x?-mx(2x-m+1)=x是不是一元二次方程,如果是,指出二次项系数及常数项.
解析:将原方程整理成一般形式得:(1-2m)x?+(m?-m-1)x=0,
当1-2m≠0,即m≠12时,原方程是一元二次方程,
二次项系数为:1-2m;常数项为0.
?
知识小结
1、一元二次方程的定义:
只含有一个未知数(一元),并且未知数的最高次为2(二次)的整式方程,叫做一元二次方程.
2、一元二次方程的一般形式及各项系数:
一般形式是ax2+bx +c=0(a≠0).其中ax2是二次项,a是二次项系数;bx是一次项,b是一次项系数;c是常数项.
课后练习
4.若方程(a-1)xa?+1+5x=4是一元二次方程,求a的值。
1.关于x的方程mx?-3x= x?-mx+2是一元二次方程,则m的取值范是 .
3.已知关于x的方程(m?-4)x?+(m-2)x+3m-1=0,
当m______时,该方程是一元二次方程;
当m=____时,该方程是一元一次方程。
2.如图,在宽为20m,长30m的矩形场地上,修筑同样宽的
两条道路,余下的部分作为耕地,要使耕地的面积为500m2,
若设路宽为x米,则可列方程为:_____________,它的一般
形式是____________,其中的二次项系数是_____,一次项
是 ,常数项是_________。
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
