人教版数学九年级 下册27.3 位似——两个位似图形坐标之间的关系课件(23张)
文档属性
| 名称 | 人教版数学九年级 下册27.3 位似——两个位似图形坐标之间的关系课件(23张) |
|
|
| 格式 | pptx | ||
| 文件大小 | 600.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-20 00:00:00 | ||
图片预览




文档简介
27.3 位 似(二)
新人教版九年级下册 第二十七章 《相 似》
学习目标
1.理解位似图形在平面直角坐标系中的对应点的坐标变化规律;
2.了解四种变换的异同,能够在图形中找出这些变换;
3.感受数形结合思想,体验合作交流探索数学的乐趣.
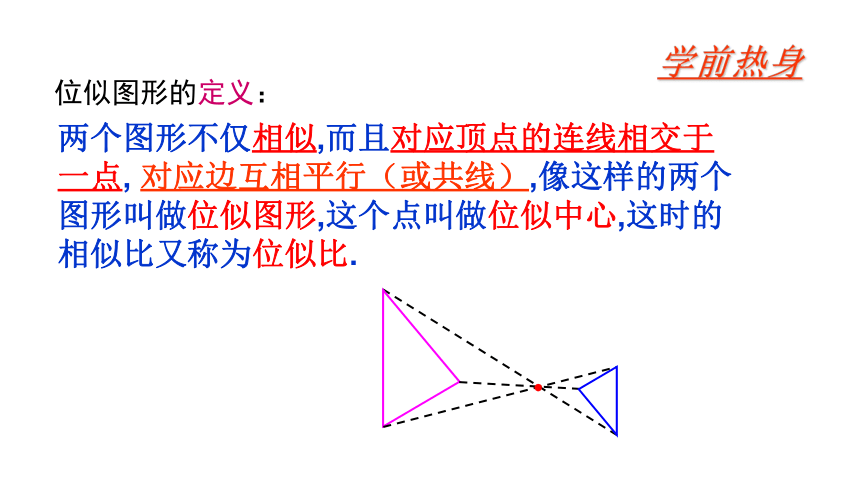
位似图形的定义:
两个图形不仅相似,而且对应顶点的连线相交于一点, 对应边互相平行(或共线),像这样的两个图形叫做位似图形,这个点叫做位似中心,这时的相似比又称为位似比.
学前热身
●
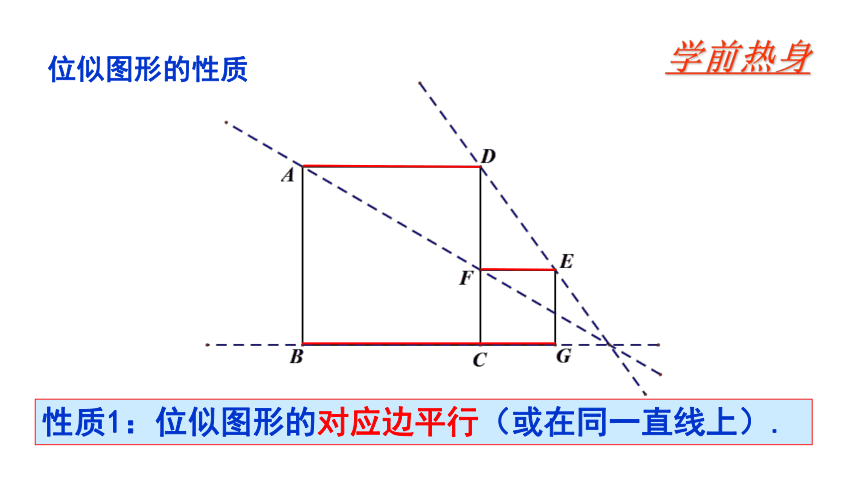
位似图形的性质
性质1:位似图形的对应边平行(或在同一直线上).
学前热身
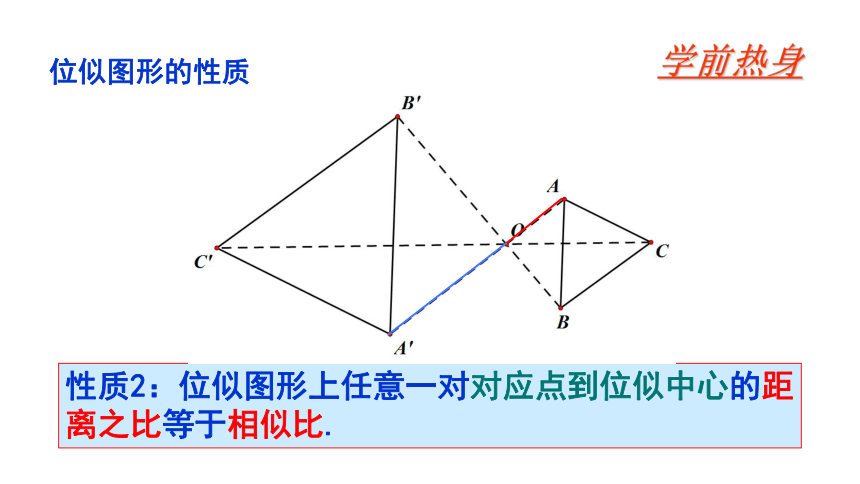
位似图形的性质
性质2:位似图形上任意一对对应点到位似中心的距离之比等于相似比.
学前热身
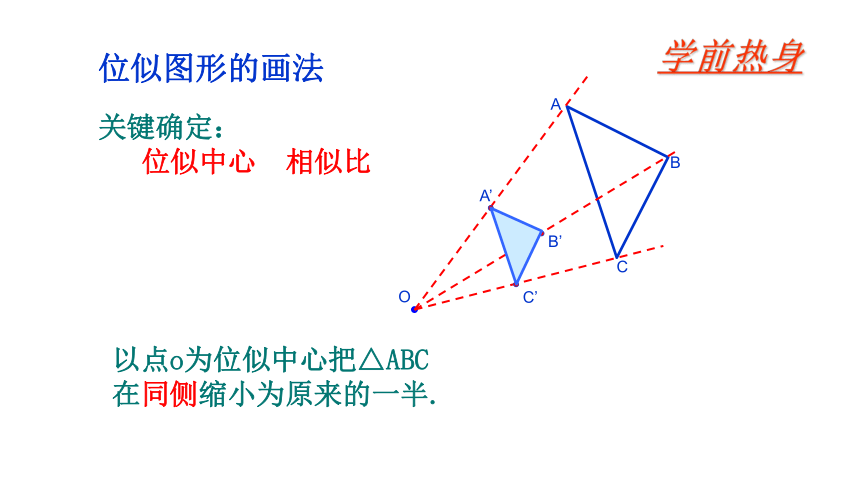
位似图形的画法
A
B
A’
C’
B’
C
O
以点o为位似中心把△ABC
在同侧缩小为原来的一半.
学前热身
关键确定:
位似中心 相似比
B’’
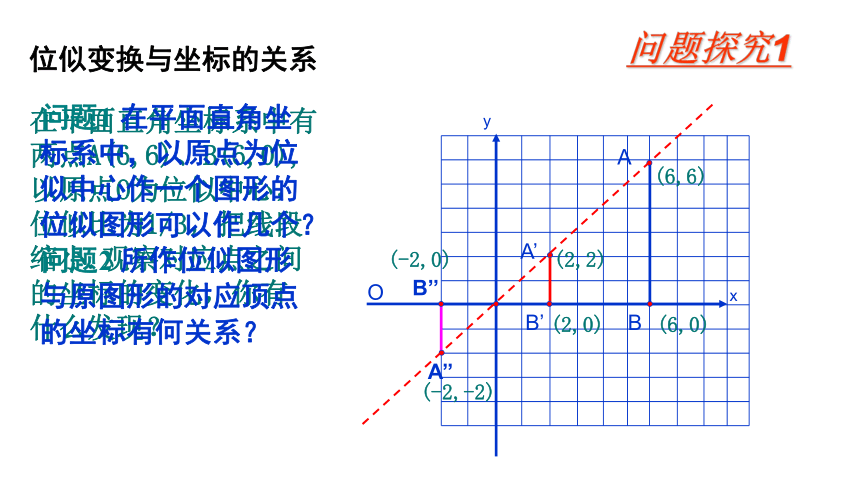
位似变换与坐标的关系
A
A’’
B’
A’
B
O
在平面直角坐标系中有
两点A(6,6)、B(6,0),
以原点O为位似中心,
位似比为1/3,把线段
缩小.观察对应点之间
的坐标的变化,你有
什么发现?
x
y
问题探究1
问题1 在平面直角坐标系中,以原点为位似中心作一个图形的位似图形可以作几个?
问题2 所作位似图形与原图形的对应顶点的坐标有何关系?
(-2,-2)
(-2,0)
(2,0)
(2,2)
(6,0)
(6,6)
2.位似图形对应点的坐标的比等于k或-k.
例如:点A(x,y)的对应点为A′,则A′点的坐标可以这样确定:
或
A′(kx,ky)
A′(-kx,-ky)
规律归纳
在平面直角坐标系中,以原点为位似中心,
所作图形与原图形相似比为k,
1.可以作两个与原图形位似的图形.
1.如果四边形ABCD的坐标分别为
A(-6,6),B(-8,2),C(-4,0),D(-2,4),
写出以原点为位似中心,位似比为1:2的
一个缩小图形的对应点的坐标.
巩固训练
A′(-3,3),B′(-4,1),C′(-2,0),D′(-1,2).
或
A′′(3,-3),B′′(4,-1),C′′(2,0),D′′ (1,-2).
x
y
o
例题.在平面直角坐标系中, 四边形ABCD的四个顶点的坐标分别为A(-6,6),B(-8,2),C(-4,0),D(-2,4),画出它的一个以原点O为位似中心,位似比为1:2的位似图形.
A′( -3,3 ), B′( -4,1 ), C′( -2,0 ), D′( -1,2 )
B
A
C
D
A′
B′
C′
D′
x
y
o
A′′ (3,-3 ), B′′ ( 4,-1 ), C′′ ( 2,0 ), D′′ ( 1,-2 )
B
A
C
D
D ′′
A ′′
B ′′
C ′′
1. 在平面直角坐标系中,四边形 OABC 的顶点坐标分别为 O (0,0),A (6,0),B (3,6),C (-3,3). 以原点 O 为位似中心,画出四边形 OABC 的位似图形,使它与四边形 OABC 的相似是 2 : 3.
巩固训练
投影—“动”悉重难点
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
O
C
解:画法一:将四边形 OABC 各顶点的坐
标都乘 ;在平面直角坐标系中描点O (0,0),A' (4,0),B' (2,4),C′ (-2,2),用线段顺次连接O,A',B',C'.
2
4
6
4
6
B'
-2
-4
-4
x
y
A
B
A'
C'
画法二:将四边形 OABC 各顶点的坐
标都乘 ;在平面
直角坐标系中描点
O (0,0),A″ (-4,0),B″ (-2,-4),C″ (2,-2),用线段顺次连接O,A″,B″,C″.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
O
C
2
4
6
4
6
B″
-2
-4
-4
x
y
A
B
A″
C″
2. △ABC 三个顶点 A (3,6),B (6,2),C (2,-1),
以原点为位似中心,得到的位似图形 △A′B′C′ 三
个顶点分别为 A′ (1,2),B′ (2, ),C′ ( , ),
则 △A′B′C′ 与 △ABC 的位似比是
1 : 3
巩固训练
若△A′B′C′ 三个顶点分别为A′ (-1,-2),
B′ (-2,- ),C′ ( - , ),位似比是多少?
至此,我们己经学习了四种变换:平移、轴对称、旋转和位似。
在平面直角坐标系中,可以利用变换前后两个图形对应顶点的坐标之间的关系表示某些变换。
在图所示的图案中,你能找到这些变换吗?
1. 将平面直角坐标系中某个图形的各点坐标做如下变化,其中属于位似变换的是 ( )
A. 将各点的纵坐标乘以 -1,横坐标不变
B. 将各点的横坐标乘以 -1,纵坐标不变
C. 将各点的横坐标、纵坐标都乘以 2
D. 将各点的纵坐标减去 3,横坐标加上 5
C
巩固训练
如图,小朋在坐标系中以A为位似中心画了两个位似的直角三角形,可不小心把 E 点弄脏了,则
E 点坐标为 ( )
A.(4,-3) B.(4,-2)
C.(4,-4) D.(4,-6)
A
问题探究2
1.如图,△ABC中,A、B两点在x轴的上方,点C的坐标是(-1,0),以点C为位似中心,在x轴的下方作△ABC的位似图形△A'B'C,并把△ABC的边长放大到原来的2倍,设点B的对应点B'的横坐标是2,求点B的横坐标。
中考链接
本节课你有哪些收获?
课堂小结
平面直角坐标系中的位似
平面直角坐标系中的位似变换
平面直角坐标系中的四种图形变换
坐标变化规律
平面直角坐标系中的位似图形的画法
课堂小结
1.作业本:课本P51,习题27.3
第3题,第5题;
2.基础训练:P140-141,27.3(2).
A组、B组.
作业
感悟
●
谢谢!
新人教版九年级下册 第二十七章 《相 似》
学习目标
1.理解位似图形在平面直角坐标系中的对应点的坐标变化规律;
2.了解四种变换的异同,能够在图形中找出这些变换;
3.感受数形结合思想,体验合作交流探索数学的乐趣.
位似图形的定义:
两个图形不仅相似,而且对应顶点的连线相交于一点, 对应边互相平行(或共线),像这样的两个图形叫做位似图形,这个点叫做位似中心,这时的相似比又称为位似比.
学前热身
●
位似图形的性质
性质1:位似图形的对应边平行(或在同一直线上).
学前热身
位似图形的性质
性质2:位似图形上任意一对对应点到位似中心的距离之比等于相似比.
学前热身
位似图形的画法
A
B
A’
C’
B’
C
O
以点o为位似中心把△ABC
在同侧缩小为原来的一半.
学前热身
关键确定:
位似中心 相似比
B’’
位似变换与坐标的关系
A
A’’
B’
A’
B
O
在平面直角坐标系中有
两点A(6,6)、B(6,0),
以原点O为位似中心,
位似比为1/3,把线段
缩小.观察对应点之间
的坐标的变化,你有
什么发现?
x
y
问题探究1
问题1 在平面直角坐标系中,以原点为位似中心作一个图形的位似图形可以作几个?
问题2 所作位似图形与原图形的对应顶点的坐标有何关系?
(-2,-2)
(-2,0)
(2,0)
(2,2)
(6,0)
(6,6)
2.位似图形对应点的坐标的比等于k或-k.
例如:点A(x,y)的对应点为A′,则A′点的坐标可以这样确定:
或
A′(kx,ky)
A′(-kx,-ky)
规律归纳
在平面直角坐标系中,以原点为位似中心,
所作图形与原图形相似比为k,
1.可以作两个与原图形位似的图形.
1.如果四边形ABCD的坐标分别为
A(-6,6),B(-8,2),C(-4,0),D(-2,4),
写出以原点为位似中心,位似比为1:2的
一个缩小图形的对应点的坐标.
巩固训练
A′(-3,3),B′(-4,1),C′(-2,0),D′(-1,2).
或
A′′(3,-3),B′′(4,-1),C′′(2,0),D′′ (1,-2).
x
y
o
例题.在平面直角坐标系中, 四边形ABCD的四个顶点的坐标分别为A(-6,6),B(-8,2),C(-4,0),D(-2,4),画出它的一个以原点O为位似中心,位似比为1:2的位似图形.
A′( -3,3 ), B′( -4,1 ), C′( -2,0 ), D′( -1,2 )
B
A
C
D
A′
B′
C′
D′
x
y
o
A′′ (3,-3 ), B′′ ( 4,-1 ), C′′ ( 2,0 ), D′′ ( 1,-2 )
B
A
C
D
D ′′
A ′′
B ′′
C ′′
1. 在平面直角坐标系中,四边形 OABC 的顶点坐标分别为 O (0,0),A (6,0),B (3,6),C (-3,3). 以原点 O 为位似中心,画出四边形 OABC 的位似图形,使它与四边形 OABC 的相似是 2 : 3.
巩固训练
投影—“动”悉重难点
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
O
C
解:画法一:将四边形 OABC 各顶点的坐
标都乘 ;在平面直角坐标系中描点O (0,0),A' (4,0),B' (2,4),C′ (-2,2),用线段顺次连接O,A',B',C'.
2
4
6
4
6
B'
-2
-4
-4
x
y
A
B
A'
C'
画法二:将四边形 OABC 各顶点的坐
标都乘 ;在平面
直角坐标系中描点
O (0,0),A″ (-4,0),B″ (-2,-4),C″ (2,-2),用线段顺次连接O,A″,B″,C″.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
O
C
2
4
6
4
6
B″
-2
-4
-4
x
y
A
B
A″
C″
2. △ABC 三个顶点 A (3,6),B (6,2),C (2,-1),
以原点为位似中心,得到的位似图形 △A′B′C′ 三
个顶点分别为 A′ (1,2),B′ (2, ),C′ ( , ),
则 △A′B′C′ 与 △ABC 的位似比是
1 : 3
巩固训练
若△A′B′C′ 三个顶点分别为A′ (-1,-2),
B′ (-2,- ),C′ ( - , ),位似比是多少?
至此,我们己经学习了四种变换:平移、轴对称、旋转和位似。
在平面直角坐标系中,可以利用变换前后两个图形对应顶点的坐标之间的关系表示某些变换。
在图所示的图案中,你能找到这些变换吗?
1. 将平面直角坐标系中某个图形的各点坐标做如下变化,其中属于位似变换的是 ( )
A. 将各点的纵坐标乘以 -1,横坐标不变
B. 将各点的横坐标乘以 -1,纵坐标不变
C. 将各点的横坐标、纵坐标都乘以 2
D. 将各点的纵坐标减去 3,横坐标加上 5
C
巩固训练
如图,小朋在坐标系中以A为位似中心画了两个位似的直角三角形,可不小心把 E 点弄脏了,则
E 点坐标为 ( )
A.(4,-3) B.(4,-2)
C.(4,-4) D.(4,-6)
A
问题探究2
1.如图,△ABC中,A、B两点在x轴的上方,点C的坐标是(-1,0),以点C为位似中心,在x轴的下方作△ABC的位似图形△A'B'C,并把△ABC的边长放大到原来的2倍,设点B的对应点B'的横坐标是2,求点B的横坐标。
中考链接
本节课你有哪些收获?
课堂小结
平面直角坐标系中的位似
平面直角坐标系中的位似变换
平面直角坐标系中的四种图形变换
坐标变化规律
平面直角坐标系中的位似图形的画法
课堂小结
1.作业本:课本P51,习题27.3
第3题,第5题;
2.基础训练:P140-141,27.3(2).
A组、B组.
作业
感悟
●
谢谢!
