第17章 函数及其图象达标检测题(含答案)
文档属性
| 名称 | 第17章 函数及其图象达标检测题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-20 15:02:32 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
华师大版八年级数学下册
第17章达标检测题
(考试时间:120分钟 满分:120分)
第Ⅰ卷(选择题 共24分)
一、选择题(本大题共8小题,每小题3分,共24分)
1.(黄冈中考)在函数y=中,自变量x的取值范围是
( )
A.x>0
B.x≥-4
C.x≥-4且x≠0
D.x>0且x≠-1
2.某人匀速跑步到公园,在公园里某处停留了一段时间,再沿原路匀速步行回家,表示此人离家的距离y与时间x的关系的大致图象是( )
3.一次函数y=-x+2的图象不经过的象限是( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
4.如图,已知直线y1=x+m与y2=kx-1相交于点P(-1,1),则关于x的不等式x+m>kx-1的解集在数轴上表示正确的是( )
5.若ab<0,则正比例函数y=ax与反比例函数y=在同一坐标系中的大致图象可能是( )
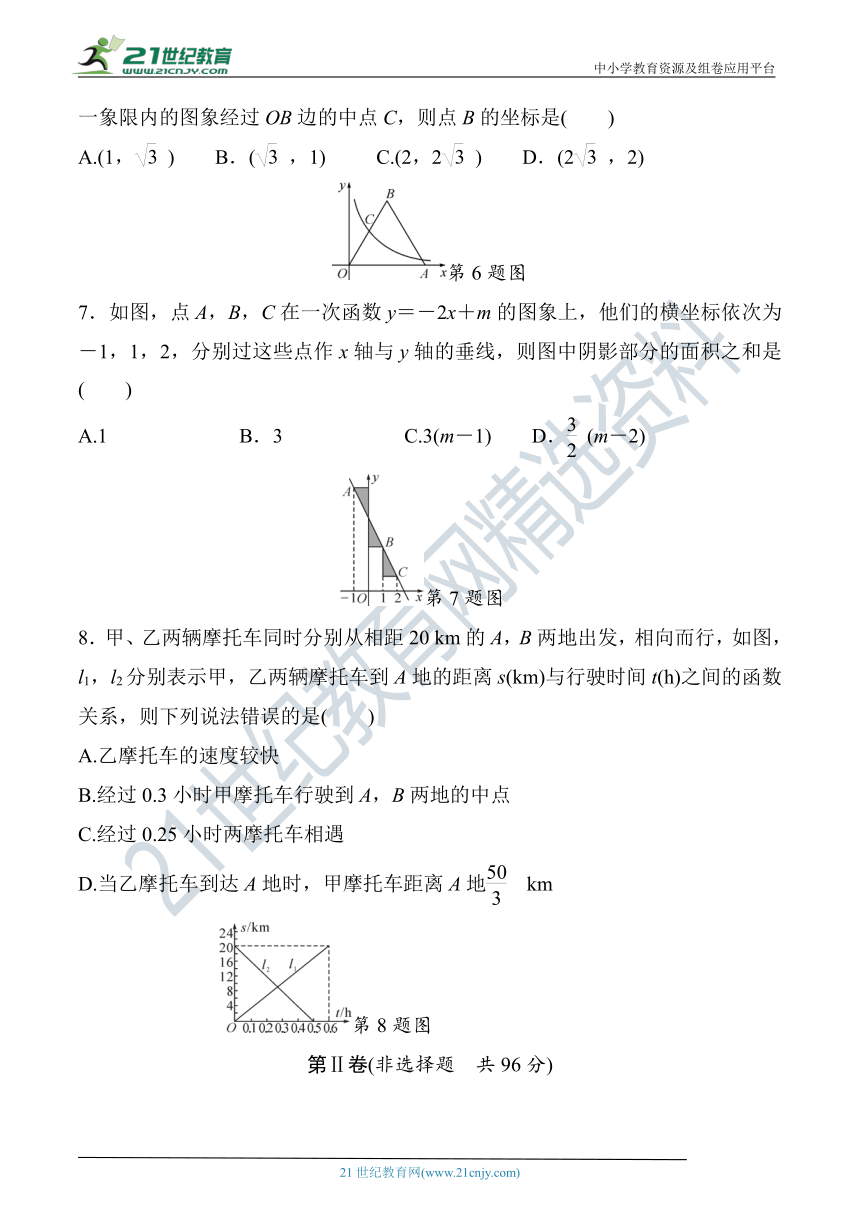
(临沂中考)如图,等边三角形OAB的一边OA在x轴上,双曲线y=在第一象限内的图象经过OB边的中点C,则点B的坐标是( )
A.(1,)
B.(,1)
C.(2,2)
D.(2,2)
第6题图
7.如图,点A,B,C在一次函数y=-2x+m的图象上,他们的横坐标依次为-1,1,2,分别过这些点作x轴与y轴的垂线,则图中阴影部分的面积之和是( )
A.1
B.3
C.3(m-1)
D.(m-2)
第7题图
8.甲、乙两辆摩托车同时分别从相距20
km的A,B两地出发,相向而行,如图,l1,l2分别表示甲,乙两辆摩托车到A地的距离s(km)与行驶时间t(h)之间的函数关系,则下列说法错误的是( )
A.乙摩托车的速度较快
B.经过0.3小时甲摩托车行驶到A,B两地的中点
C.经过0.25小时两摩托车相遇
D.当乙摩托车到达A地时,甲摩托车距离A地
km
第8题图
第Ⅱ卷(非选择题 共96分)
二、填空题(本大题共8小题,每小题3分,共24分)
9.若y=(a+3)x+a2-9是正比例函数,则a=
.
10.某书定价8元,如果购买10本以上,超过10本的部分打八折,请写出购买数量x(本)(x>10)与付款金额y(元)之间的关系式
.
11.已知点A(-5,a),B(4,b)在直线y=-3x+2上,则a
b.(选填“>”“<”或“=”)
12.已知点A(x,1)与点B(2,y)关于y轴对称,则(x+y)2
021的值为
.
13.如图所示,直线AB是一次函数y=kx+b的图象,若AB=,则函数的表达式为
.
第13题图
14.如图,过y轴正半轴上的任意一点P,作x轴的平行线,分别与反比例函数y=-和y=的图象交于点A和点B,若点C是x轴上任意一点,连结AC,BC,则△ABC的面积为
.
第14题图
15.一个装有进水管和出水管的容器,从某时刻起只打开进水管进水,经过一段时间,再打开出水管放水,至12分钟时,关停进水管,在打开进水管到关进水管这段时间内,容器内的水量y(单位/升)与时间x(单位:分钟)之间的函数关系如图所示,关停进水管后,经过
分钟容器中的水恰好放完.
第15题图
16.如图,一次函数y=-x+b与反比例函数y=(x>0)的图象交于A,B两点,与x轴,y轴分别交于C,D两点,连结OA,OB,过点A作AE⊥x轴于点E,交OB于点F,设点A的横坐标为m,则b=
.(用含m的代数式表示)
第16题图
三、解答题(本大题共8小题,共72分)
17.(10分)已知一次函数y=(3+m)x+n-6.
(1)当m,n为何值时,函数的图象过原点?
(2)当m,n满足什么条件时,函数的图象经过第一、二、三象限?
18.(6分)判断A(-2,-5),B(3,5),C(7,13)三点是否在一条直线上,并说明理由.
19.(8分)已知直线y=2x+3与直线y=-2x-1.
(1)若两直线与y轴分别交于点A,B,求点A,B的坐标;
(2)求两直线的交点C的坐标;
(3)求△ABC的面积.
20.(8分)如图,已知某电路的电压U(V)、电流I(A)、电阻R(Ω)三者之间有如下关系式:U=IR,且该电路的电压U恒为220
V.
(1)求出电流I关于电阻R的函数表达式;
(2)如果该电路的电阻为200
Ω,则通过他的电流是多少?
21.(8分)如图,一次函数y1=kx+b(k≠0)和反比例函数y2=(m≠0)的图象交于点A(-1,6),B(a,-2).
(1)求一次函数与反比例函数的表达式;
(2)根据图象直接写出y1>y2时,x的取值范围.
22.(10分)(泸州中考)某工厂现有甲种原料380千克,乙种原料290千克,计划用这两种原料生产A,B两种产品共50件.已知生产一件A产品需要甲种原料9千克,乙种原料3千克,可获利700元;生产一件B产品需要甲种原料4千克,乙种原料10千克,可获利1
200元.设生产A,B两种产品的总利润为y元,其中A种产品生产的件数是x.
(1)写出y与x之间的函数关系式;
(2)如何安排A,B两种产品的生产件数,使总利润y有最大值,并求出y的最大值.
23.(10分)甲、乙两名大学生去距学校36千米的某乡镇进行社会调查.他们从学校出发,骑电动车行驶20分钟时发现忘带相机,甲下车步行前往,乙骑电动车沿原路返回.乙取到相机后(在学校取相机所用时间忽略不计),骑电动车追甲,在距乡镇13.5千米处追上甲并同车前往乡镇.若电动车速度始终不变,设甲与学校相距y甲(千米),乙与学校相距y乙(千米),甲离开学校的时间为x(分),y甲,y乙与x之间的函数图象如图所示.结合图象解答下列问题:
(1)电动车的速度为
千米/分;
(2)甲步行所用的时间为
分钟;
(3)求乙返回到学校时,甲与学校相距多远.
24.(12分)某个体户购进一批时令水果,20天销售完毕.他将本次销售情况进行了跟踪记录,根据所记录的数据可绘制如图所示的函数图象,其中日销售量y(千克)与销售时间x(天)之间的函数关系如图甲所示,销售单价p(元/千克)与销售时间x(天)之间的函数关系如图乙所示.
(1)直接写出y与x之间的函数关系式;
(2)分别求出第10天和第15天的销售金额;
(3)若日销售量不低于24千克的时间段为“最佳销售期”,则此次销售过程中“最佳销售期”共有多少天?在此期间销售单价最高为多少元/千克?
参考答案
第Ⅰ卷(选择题 共24分)
一、选择题(本大题共8小题,每小题3分,共24分)
1.(黄冈中考)在函数y=中,自变量x的取值范围是
( C )
A.x>0
B.x≥-4
C.x≥-4且x≠0
D.x>0且x≠-1
2.某人匀速跑步到公园,在公园里某处停留了一段时间,再沿原路匀速步行回家,表示此人离家的距离y与时间x的关系的大致图象是
( B )
3.一次函数y=-x+2的图象不经过的象限是
( C )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
4.如图,已知直线y1=x+m与y2=kx-1相交于点P(-1,1),则关于x的不等式x+m>kx-1的解集在数轴上表示正确的是
( B )
5.若ab<0,则正比例函数y=ax与反比例函数y=在同一坐标系中的大致图象可能是
( B )
(临沂中考)如图,等边三角形OAB的一边OA在x轴上,双曲线y=在第一象限内的图象经过OB边的中点C,则点B的坐标是
( C )
A.(1,)
B.(,1)
C.(2,2)
D.(2,2)
第6题图
7.如图,点A,B,C在一次函数y=-2x+m的图象上,他们的横坐标依次为-1,1,2,分别过这些点作x轴与y轴的垂线,则图中阴影部分的面积之和是
( B )
A.1
B.3
C.3(m-1)
D.(m-2)
第7题图
8.甲、乙两辆摩托车同时分别从相距20
km的A,B两地出发,相向而行,如图,l1,l2分别表示甲,乙两辆摩托车到A地的距离s(km)与行驶时间t(h)之间的函数关系,则下列说法错误的是
( C )
A.乙摩托车的速度较快
B.经过0.3小时甲摩托车行驶到A,B两地的中点
C.经过0.25小时两摩托车相遇
D.当乙摩托车到达A地时,甲摩托车距离A地
km
第8题图
第Ⅱ卷(非选择题 共96分)
二、填空题(本大题共8小题,每小题3分,共24分)
9.若y=(a+3)x+a2-9是正比例函数,则a=__3__.
10.某书定价8元,如果购买10本以上,超过10本的部分打八折,请写出购买数量x(本)(x>10)与付款金额y(元)之间的关系式__y=6.4x+16(x>10)__.
11.已知点A(-5,a),B(4,b)在直线y=-3x+2上,则a__>__b.(选填“>”“<”或“=”)
12.已知点A(x,1)与点B(2,y)关于y轴对称,则(x+y)2
019的值为__-1__.
13.如图所示,直线AB是一次函数y=kx+b的图象,若AB=,则函数的表达式为__y=-2x+2__.
第13题图
14.如图,过y轴正半轴上的任意一点P,作x轴的平行线,分别与反比例函数y=-和y=的图象交于点A和点B,若点C是x轴上任意一点,连结AC,BC,则△ABC的面积为__3__.
第14题图
15.一个装有进水管和出水管的容器,从某时刻起只打开进水管进水,经过一段时间,再打开出水管放水,至12分钟时,关停进水管,在打开进水管到关进水管这段时间内,容器内的水量y(单位/升)与时间x(单位:分钟)之间的函数关系如图所示,关停进水管后,经过__8__分钟容器中的水恰好放完.
第15题图
16.如图,一次函数y=-x+b与反比例函数y=(x>0)的图象交于A,B两点,与x轴,y轴分别交于C,D两点,连结OA,OB,过点A作AE⊥x轴于点E,交OB于点F,设点A的横坐标为m,则b=__m+__.(用含m的代数式表示)
第16题图
三、解答题(本大题共8小题,共72分)
17.(10分)已知一次函数y=(3+m)x+n-6.
(1)当m,n为何值时,函数的图象过原点?
(2)当m,n满足什么条件时,函数的图象经过第一、二、三象限?
解:(1)依题意得
n-6=0,))
得m≠-3且n=6.
∵该函数图象经过第一、二、三象限,
∴
n-6>0,))
解得m>-3且n>6.
18.(6分)判断A(-2,-5),B(3,5),C(7,13)三点是否在一条直线上,并说明理由.
解:A,B,C三点在同一条直线上,
设经过A,B两点的直线表达式是y=kx+b(k≠0),
∴
5=3k+b,))
∴
b=-1.))
∴y=2x-1,当x=7时,y=2×7-1=13,
∴点C在直线AB上,即A,B,C三点在同一条直线上.
19.(8分)已知直线y=2x+3与直线y=-2x-1.
(1)若两直线与y轴分别交于点A,B,求点A,B的坐标;
(2)求两直线的交点C的坐标;
(3)求△ABC的面积.
解:(1)对于y=2x+3,令x=0,
则y=3.∴点A的坐标为(0,3).
对于y=-2x-1,令x=0,则y=-1.∴点B的坐标为(0,-1).
(2)解方程组
y=-2x-1,))
得
y=1.))
∴点C的坐标为(-1,1).
(3)△ABC的面积为×[3-(-1)]×|-1|=2.
20.(8分)如图,已知某电路的电压U(V)、电流I(A)、电阻R(Ω)三者之间有如下关系式:U=IR,且该电路的电压U恒为220
V.
(1)求出电流I关于电阻R的函数表达式;
(2)如果该电路的电阻为200
Ω,则通过他的电流是多少?
解:(1)电流I关于电阻R的函数表达式是I=(R>0);
(2)通过他的电流是=1.1
A.
21.(8分)如图,一次函数y1=kx+b(k≠0)和反比例函数y2=(m≠0)的图象交于点A(-1,6),B(a,-2).
(1)求一次函数与反比例函数的表达式;
(2)根据图象直接写出y1>y2时,x的取值范围.
解:(1)把点A(-1,6)代入反比例函数y2=(m≠0),
得m=-1×6=-6,∴y2=-.
将B(a,-2)代入y2=-,得-2=,
解得a=3,∴B(3,-2).
将A(-1,6),B(3,-2)代入一次函数y1=kx+b,
得
3k+b=-2,))
解得
b=4.))
∴y1=-2x+4.
(2)由函数图象可得当y1>y2时,x<-1或022.(10分)(泸州中考)某工厂现有甲种原料380千克,乙种原料290千克,计划用这两种原料生产A,B两种产品共50件.已知生产一件A产品需要甲种原料9千克,乙种原料3千克,可获利700元;生产一件B产品需要甲种原料4千克,乙种原料10千克,可获利1
200元.设生产A,B两种产品的总利润为y元,其中A种产品生产的件数是x.
(1)写出y与x之间的函数关系式;
(2)如何安排A,B两种产品的生产件数,使总利润y有最大值,并求出y的最大值.
解:(1)y=700x+1
200(50-x),即y=-500x+60
000;
(2)由题意得
3x+10(50-x)≤290,))
解得30≤x≤36,y=-500x+60
000,
y随x的增大而减小,
当x=30时,y最大=45
000,生产B种产品20件,
A种产品30件,总利润y有最大值,y最大=45
000元.
23.(10分)甲、乙两名大学生去距学校36千米的某乡镇进行社会调查.他们从学校出发,骑电动车行驶20分钟时发现忘带相机,甲下车步行前往,乙骑电动车沿原路返回.乙取到相机后(在学校取相机所用时间忽略不计),骑电动车追甲,在距乡镇13.5千米处追上甲并同车前往乡镇.若电动车速度始终不变,设甲与学校相距y甲(千米),乙与学校相距y乙(千米),甲离开学校的时间为x(分),y甲,y乙与x之间的函数图象如图所示.结合图象解答下列问题:
(1)电动车的速度为__0.9__千米/分;
(2)甲步行所用的时间为__45__分钟;
(3)求乙返回到学校时,甲与学校相距多远.
解:甲步行过程中,设y甲与x的函数关系式为y甲=kx+b,
则
65k+b=22.5,))
解得
b=16,))
∴y甲=0.1x+16,当x=40时,y甲=20.
即乙返回到学校时,甲与学校相距20千米.
24.(12分)某个体户购进一批时令水果,20天销售完毕.他将本次销售情况进行了跟踪记录,根据所记录的数据可绘制如图所示的函数图象,其中日销售量y(千克)与销售时间x(天)之间的函数关系如图甲所示,销售单价p(元/千克)与销售时间x(天)之间的函数关系如图乙所示.
(1)直接写出y与x之间的函数关系式;
(2)分别求出第10天和第15天的销售金额;
(3)若日销售量不低于24千克的时间段为“最佳销售期”,则此次销售过程中“最佳销售期”共有多少天?在此期间销售单价最高为多少元/千克?
解:(1)y=
-6x+120(15设销售单价p(元/千克)与销售时间x(天)之间的函数关系式为
p=kx+b(10≤x≤20),把点(10,10),(20,8)代入,
得
20k+b=8,))
解得
b=12.))
∴p=-x+12(10≤x≤20).
当x=15时,p=-×15+12=9.
第10天的销售金额为2×10×10=200元,
第15天的销售金额为30×9=270元.
(3)当y≥24时,①24≤2x≤30,解得12≤x≤15;
②24≤-6x+120<30.解得15综上可知“最佳销售期”的范围是12≤x≤16,共有5天.
对于函数p=-x+12(10≤x≤20),y随x的值的增大而减小,
故当x=12时,p有最大值,最高单价为-×12+12=9.6元/千克.
)
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
华师大版八年级数学下册
第17章达标检测题
(考试时间:120分钟 满分:120分)
第Ⅰ卷(选择题 共24分)
一、选择题(本大题共8小题,每小题3分,共24分)
1.(黄冈中考)在函数y=中,自变量x的取值范围是
( )
A.x>0
B.x≥-4
C.x≥-4且x≠0
D.x>0且x≠-1
2.某人匀速跑步到公园,在公园里某处停留了一段时间,再沿原路匀速步行回家,表示此人离家的距离y与时间x的关系的大致图象是( )
3.一次函数y=-x+2的图象不经过的象限是( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
4.如图,已知直线y1=x+m与y2=kx-1相交于点P(-1,1),则关于x的不等式x+m>kx-1的解集在数轴上表示正确的是( )
5.若ab<0,则正比例函数y=ax与反比例函数y=在同一坐标系中的大致图象可能是( )
(临沂中考)如图,等边三角形OAB的一边OA在x轴上,双曲线y=在第一象限内的图象经过OB边的中点C,则点B的坐标是( )
A.(1,)
B.(,1)
C.(2,2)
D.(2,2)
第6题图
7.如图,点A,B,C在一次函数y=-2x+m的图象上,他们的横坐标依次为-1,1,2,分别过这些点作x轴与y轴的垂线,则图中阴影部分的面积之和是( )
A.1
B.3
C.3(m-1)
D.(m-2)
第7题图
8.甲、乙两辆摩托车同时分别从相距20
km的A,B两地出发,相向而行,如图,l1,l2分别表示甲,乙两辆摩托车到A地的距离s(km)与行驶时间t(h)之间的函数关系,则下列说法错误的是( )
A.乙摩托车的速度较快
B.经过0.3小时甲摩托车行驶到A,B两地的中点
C.经过0.25小时两摩托车相遇
D.当乙摩托车到达A地时,甲摩托车距离A地
km
第8题图
第Ⅱ卷(非选择题 共96分)
二、填空题(本大题共8小题,每小题3分,共24分)
9.若y=(a+3)x+a2-9是正比例函数,则a=
.
10.某书定价8元,如果购买10本以上,超过10本的部分打八折,请写出购买数量x(本)(x>10)与付款金额y(元)之间的关系式
.
11.已知点A(-5,a),B(4,b)在直线y=-3x+2上,则a
b.(选填“>”“<”或“=”)
12.已知点A(x,1)与点B(2,y)关于y轴对称,则(x+y)2
021的值为
.
13.如图所示,直线AB是一次函数y=kx+b的图象,若AB=,则函数的表达式为
.
第13题图
14.如图,过y轴正半轴上的任意一点P,作x轴的平行线,分别与反比例函数y=-和y=的图象交于点A和点B,若点C是x轴上任意一点,连结AC,BC,则△ABC的面积为
.
第14题图
15.一个装有进水管和出水管的容器,从某时刻起只打开进水管进水,经过一段时间,再打开出水管放水,至12分钟时,关停进水管,在打开进水管到关进水管这段时间内,容器内的水量y(单位/升)与时间x(单位:分钟)之间的函数关系如图所示,关停进水管后,经过
分钟容器中的水恰好放完.
第15题图
16.如图,一次函数y=-x+b与反比例函数y=(x>0)的图象交于A,B两点,与x轴,y轴分别交于C,D两点,连结OA,OB,过点A作AE⊥x轴于点E,交OB于点F,设点A的横坐标为m,则b=
.(用含m的代数式表示)
第16题图
三、解答题(本大题共8小题,共72分)
17.(10分)已知一次函数y=(3+m)x+n-6.
(1)当m,n为何值时,函数的图象过原点?
(2)当m,n满足什么条件时,函数的图象经过第一、二、三象限?
18.(6分)判断A(-2,-5),B(3,5),C(7,13)三点是否在一条直线上,并说明理由.
19.(8分)已知直线y=2x+3与直线y=-2x-1.
(1)若两直线与y轴分别交于点A,B,求点A,B的坐标;
(2)求两直线的交点C的坐标;
(3)求△ABC的面积.
20.(8分)如图,已知某电路的电压U(V)、电流I(A)、电阻R(Ω)三者之间有如下关系式:U=IR,且该电路的电压U恒为220
V.
(1)求出电流I关于电阻R的函数表达式;
(2)如果该电路的电阻为200
Ω,则通过他的电流是多少?
21.(8分)如图,一次函数y1=kx+b(k≠0)和反比例函数y2=(m≠0)的图象交于点A(-1,6),B(a,-2).
(1)求一次函数与反比例函数的表达式;
(2)根据图象直接写出y1>y2时,x的取值范围.
22.(10分)(泸州中考)某工厂现有甲种原料380千克,乙种原料290千克,计划用这两种原料生产A,B两种产品共50件.已知生产一件A产品需要甲种原料9千克,乙种原料3千克,可获利700元;生产一件B产品需要甲种原料4千克,乙种原料10千克,可获利1
200元.设生产A,B两种产品的总利润为y元,其中A种产品生产的件数是x.
(1)写出y与x之间的函数关系式;
(2)如何安排A,B两种产品的生产件数,使总利润y有最大值,并求出y的最大值.
23.(10分)甲、乙两名大学生去距学校36千米的某乡镇进行社会调查.他们从学校出发,骑电动车行驶20分钟时发现忘带相机,甲下车步行前往,乙骑电动车沿原路返回.乙取到相机后(在学校取相机所用时间忽略不计),骑电动车追甲,在距乡镇13.5千米处追上甲并同车前往乡镇.若电动车速度始终不变,设甲与学校相距y甲(千米),乙与学校相距y乙(千米),甲离开学校的时间为x(分),y甲,y乙与x之间的函数图象如图所示.结合图象解答下列问题:
(1)电动车的速度为
千米/分;
(2)甲步行所用的时间为
分钟;
(3)求乙返回到学校时,甲与学校相距多远.
24.(12分)某个体户购进一批时令水果,20天销售完毕.他将本次销售情况进行了跟踪记录,根据所记录的数据可绘制如图所示的函数图象,其中日销售量y(千克)与销售时间x(天)之间的函数关系如图甲所示,销售单价p(元/千克)与销售时间x(天)之间的函数关系如图乙所示.
(1)直接写出y与x之间的函数关系式;
(2)分别求出第10天和第15天的销售金额;
(3)若日销售量不低于24千克的时间段为“最佳销售期”,则此次销售过程中“最佳销售期”共有多少天?在此期间销售单价最高为多少元/千克?
参考答案
第Ⅰ卷(选择题 共24分)
一、选择题(本大题共8小题,每小题3分,共24分)
1.(黄冈中考)在函数y=中,自变量x的取值范围是
( C )
A.x>0
B.x≥-4
C.x≥-4且x≠0
D.x>0且x≠-1
2.某人匀速跑步到公园,在公园里某处停留了一段时间,再沿原路匀速步行回家,表示此人离家的距离y与时间x的关系的大致图象是
( B )
3.一次函数y=-x+2的图象不经过的象限是
( C )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
4.如图,已知直线y1=x+m与y2=kx-1相交于点P(-1,1),则关于x的不等式x+m>kx-1的解集在数轴上表示正确的是
( B )
5.若ab<0,则正比例函数y=ax与反比例函数y=在同一坐标系中的大致图象可能是
( B )
(临沂中考)如图,等边三角形OAB的一边OA在x轴上,双曲线y=在第一象限内的图象经过OB边的中点C,则点B的坐标是
( C )
A.(1,)
B.(,1)
C.(2,2)
D.(2,2)
第6题图
7.如图,点A,B,C在一次函数y=-2x+m的图象上,他们的横坐标依次为-1,1,2,分别过这些点作x轴与y轴的垂线,则图中阴影部分的面积之和是
( B )
A.1
B.3
C.3(m-1)
D.(m-2)
第7题图
8.甲、乙两辆摩托车同时分别从相距20
km的A,B两地出发,相向而行,如图,l1,l2分别表示甲,乙两辆摩托车到A地的距离s(km)与行驶时间t(h)之间的函数关系,则下列说法错误的是
( C )
A.乙摩托车的速度较快
B.经过0.3小时甲摩托车行驶到A,B两地的中点
C.经过0.25小时两摩托车相遇
D.当乙摩托车到达A地时,甲摩托车距离A地
km
第8题图
第Ⅱ卷(非选择题 共96分)
二、填空题(本大题共8小题,每小题3分,共24分)
9.若y=(a+3)x+a2-9是正比例函数,则a=__3__.
10.某书定价8元,如果购买10本以上,超过10本的部分打八折,请写出购买数量x(本)(x>10)与付款金额y(元)之间的关系式__y=6.4x+16(x>10)__.
11.已知点A(-5,a),B(4,b)在直线y=-3x+2上,则a__>__b.(选填“>”“<”或“=”)
12.已知点A(x,1)与点B(2,y)关于y轴对称,则(x+y)2
019的值为__-1__.
13.如图所示,直线AB是一次函数y=kx+b的图象,若AB=,则函数的表达式为__y=-2x+2__.
第13题图
14.如图,过y轴正半轴上的任意一点P,作x轴的平行线,分别与反比例函数y=-和y=的图象交于点A和点B,若点C是x轴上任意一点,连结AC,BC,则△ABC的面积为__3__.
第14题图
15.一个装有进水管和出水管的容器,从某时刻起只打开进水管进水,经过一段时间,再打开出水管放水,至12分钟时,关停进水管,在打开进水管到关进水管这段时间内,容器内的水量y(单位/升)与时间x(单位:分钟)之间的函数关系如图所示,关停进水管后,经过__8__分钟容器中的水恰好放完.
第15题图
16.如图,一次函数y=-x+b与反比例函数y=(x>0)的图象交于A,B两点,与x轴,y轴分别交于C,D两点,连结OA,OB,过点A作AE⊥x轴于点E,交OB于点F,设点A的横坐标为m,则b=__m+__.(用含m的代数式表示)
第16题图
三、解答题(本大题共8小题,共72分)
17.(10分)已知一次函数y=(3+m)x+n-6.
(1)当m,n为何值时,函数的图象过原点?
(2)当m,n满足什么条件时,函数的图象经过第一、二、三象限?
解:(1)依题意得
n-6=0,))
得m≠-3且n=6.
∵该函数图象经过第一、二、三象限,
∴
n-6>0,))
解得m>-3且n>6.
18.(6分)判断A(-2,-5),B(3,5),C(7,13)三点是否在一条直线上,并说明理由.
解:A,B,C三点在同一条直线上,
设经过A,B两点的直线表达式是y=kx+b(k≠0),
∴
5=3k+b,))
∴
b=-1.))
∴y=2x-1,当x=7时,y=2×7-1=13,
∴点C在直线AB上,即A,B,C三点在同一条直线上.
19.(8分)已知直线y=2x+3与直线y=-2x-1.
(1)若两直线与y轴分别交于点A,B,求点A,B的坐标;
(2)求两直线的交点C的坐标;
(3)求△ABC的面积.
解:(1)对于y=2x+3,令x=0,
则y=3.∴点A的坐标为(0,3).
对于y=-2x-1,令x=0,则y=-1.∴点B的坐标为(0,-1).
(2)解方程组
y=-2x-1,))
得
y=1.))
∴点C的坐标为(-1,1).
(3)△ABC的面积为×[3-(-1)]×|-1|=2.
20.(8分)如图,已知某电路的电压U(V)、电流I(A)、电阻R(Ω)三者之间有如下关系式:U=IR,且该电路的电压U恒为220
V.
(1)求出电流I关于电阻R的函数表达式;
(2)如果该电路的电阻为200
Ω,则通过他的电流是多少?
解:(1)电流I关于电阻R的函数表达式是I=(R>0);
(2)通过他的电流是=1.1
A.
21.(8分)如图,一次函数y1=kx+b(k≠0)和反比例函数y2=(m≠0)的图象交于点A(-1,6),B(a,-2).
(1)求一次函数与反比例函数的表达式;
(2)根据图象直接写出y1>y2时,x的取值范围.
解:(1)把点A(-1,6)代入反比例函数y2=(m≠0),
得m=-1×6=-6,∴y2=-.
将B(a,-2)代入y2=-,得-2=,
解得a=3,∴B(3,-2).
将A(-1,6),B(3,-2)代入一次函数y1=kx+b,
得
3k+b=-2,))
解得
b=4.))
∴y1=-2x+4.
(2)由函数图象可得当y1>y2时,x<-1或0
200元.设生产A,B两种产品的总利润为y元,其中A种产品生产的件数是x.
(1)写出y与x之间的函数关系式;
(2)如何安排A,B两种产品的生产件数,使总利润y有最大值,并求出y的最大值.
解:(1)y=700x+1
200(50-x),即y=-500x+60
000;
(2)由题意得
3x+10(50-x)≤290,))
解得30≤x≤36,y=-500x+60
000,
y随x的增大而减小,
当x=30时,y最大=45
000,生产B种产品20件,
A种产品30件,总利润y有最大值,y最大=45
000元.
23.(10分)甲、乙两名大学生去距学校36千米的某乡镇进行社会调查.他们从学校出发,骑电动车行驶20分钟时发现忘带相机,甲下车步行前往,乙骑电动车沿原路返回.乙取到相机后(在学校取相机所用时间忽略不计),骑电动车追甲,在距乡镇13.5千米处追上甲并同车前往乡镇.若电动车速度始终不变,设甲与学校相距y甲(千米),乙与学校相距y乙(千米),甲离开学校的时间为x(分),y甲,y乙与x之间的函数图象如图所示.结合图象解答下列问题:
(1)电动车的速度为__0.9__千米/分;
(2)甲步行所用的时间为__45__分钟;
(3)求乙返回到学校时,甲与学校相距多远.
解:甲步行过程中,设y甲与x的函数关系式为y甲=kx+b,
则
65k+b=22.5,))
解得
b=16,))
∴y甲=0.1x+16,当x=40时,y甲=20.
即乙返回到学校时,甲与学校相距20千米.
24.(12分)某个体户购进一批时令水果,20天销售完毕.他将本次销售情况进行了跟踪记录,根据所记录的数据可绘制如图所示的函数图象,其中日销售量y(千克)与销售时间x(天)之间的函数关系如图甲所示,销售单价p(元/千克)与销售时间x(天)之间的函数关系如图乙所示.
(1)直接写出y与x之间的函数关系式;
(2)分别求出第10天和第15天的销售金额;
(3)若日销售量不低于24千克的时间段为“最佳销售期”,则此次销售过程中“最佳销售期”共有多少天?在此期间销售单价最高为多少元/千克?
解:(1)y=
-6x+120(15
p=kx+b(10≤x≤20),把点(10,10),(20,8)代入,
得
20k+b=8,))
解得
b=12.))
∴p=-x+12(10≤x≤20).
当x=15时,p=-×15+12=9.
第10天的销售金额为2×10×10=200元,
第15天的销售金额为30×9=270元.
(3)当y≥24时,①24≤2x≤30,解得12≤x≤15;
②24≤-6x+120<30.解得15
对于函数p=-x+12(10≤x≤20),y随x的值的增大而减小,
故当x=12时,p有最大值,最高单价为-×12+12=9.6元/千克.
)
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
