人教版数学九年级上册22.1.4y=ax_+bx+c的图像和性质课件(18张)
文档属性
| 名称 | 人教版数学九年级上册22.1.4y=ax_+bx+c的图像和性质课件(18张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 173.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-20 00:00:00 | ||
图片预览






文档简介
22.1.4 二次函数y=ax2+bx+c的图象
学习目标
1.会画y=ax2+bx+c的图象,能将一般式化为
顶点式,掌握对称轴的求法;
2.理解y=ax2+bx+c的性质.
复习旧知,导入新课
1.二次函数y=2(x-5)2+6的图象开口方向________,对称轴是________,顶点坐标是(________).它可以由函数y=2x2的图象怎样平移得到的?
2.二次函数
你能很容易地
说出它的图象的对称轴和顶点坐标吗?
X=5
向上
5 , 6
探究新知
活动1:如何确定抛物线
的开口方向、对称轴和顶点坐标
(x - 6) -18+ 21
2
=
= (x2 - 12x ) + 21
= (x2 - 12x + 36 - 36 )+ 21
探究新知
提取二次项系数
配方:加上再减去一次项系数一半的平方
整理:前三项化为完全平方式,后两项合并同类项
化简
(x - 6) + 3
2
=
探究新知
的开口方向、对称轴和顶点坐
标分别是什么?它可由二次函数y=
1.
经过
怎样平移得到的?
(x - 6) + 3
2
=
2.用描点法画出 的图象?
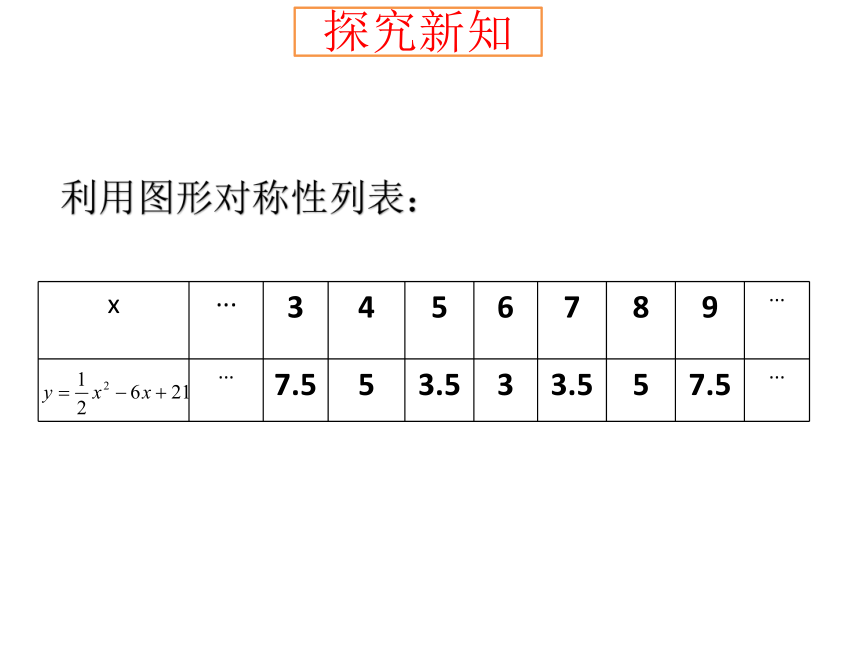
探究新知
x
···
3
4
5
6
7
8
9
···
···
7.5
5
3.5
3
3.5
5
7.5
···
利用图形对称性列表:
O
y
x
5
10
5
10
20
15
x=6
·
(6,3)
·
(8,5)
·
(4,5)
·
(9,7.5)
观察图象:在对称轴的左右两侧,抛物线从左往右的变化趋势.
当_____时y随x的增大而增大
当_____时y随x的增大而减小
x>6
x<6
(3,7.5)
(x - 6) + 3
2
=
y
由图象可知:
(1)在对称轴左侧,抛物线从左到右下降
(2)在对称轴右侧,抛物线从左到右上升
探究新知
活动2:1.不画出图象,你能直接说出函数y=-x2+2x-3的图象的开口方向、对称轴和顶点坐标吗?
y=-x2+2x-3
=-(x2-2x)-3
=-(x2-2x+1-1)-3
=-(x-1)2-2
2.你能画出函数y=-x2+2x-3的图象(草图),并说明这个函数的增减性。
探究新知
3.这个函数的最大值或最小值与函数图象的开口方向有什么关系?这个值与函数图象的顶点坐标有什么关系?
活动3:1、对于任意一个二次函数y=ax2+bx+c(a≠0),如何确定它的对称轴和顶点坐标?请写出结果。
探究新知
一般地,对于二次函数y=ax?+bx+c,我们可以利用配方化成y=a(x-h)2+k的形式导出它的对称轴和顶点坐标.
y=ax2+bx+c配方,得:
因此,其对称轴是:
顶点是: ,
x=
)
(
探究新知
2、请大家观察二次函数y=ax2+bx+c(a≠0)的图象,在对称轴的左右两侧,y随x的增大有什么变化规律?
探究新知
(1):
如果a>0,当 时,y随x的增大而减小,当
时,y随x的增大而增大.
探究新知
(2):
如果a<0,当 时,y随x
的增大而增大,当 时,
y随x的增大而减小.
当堂训练
1、写出下列抛物线的开口方向、对称轴和顶点坐标.(用顶点公式)
(1)y=3x2+2x;(2)y=-x2-2x ;
(3)y=-2x2+8x-8 (4)y=0.5x2-4x+3
1.开口向上,对称轴是x=-1/3,顶点坐标是(-1/3,-1/3)
2.开口向下,对称轴是x=-1,顶点坐标是(-1,1)
3.开口向下,对称轴是x=2,顶点坐标是(2,0)
4.开口向上,对称轴是x=4,顶点坐标是(4,-5)
2、 二次函数y=ax2+4x+a的最大值是3,则 a=________.
当堂训练
3、求二次函数y=mx2+2mx+3(m>0)的图象的对称轴。
-1
x=-1
4、抛物线y=ax2+2x+c的顶点是(-1,2),则a,c的值分别是多少?
当堂训练
a=1,c=3
5、已知抛物线y=x2-2ax+9的顶点在坐标轴
上,求a的值
a=0或±3
课堂小结
本节课你学到了哪些知识?
学习目标
1.会画y=ax2+bx+c的图象,能将一般式化为
顶点式,掌握对称轴的求法;
2.理解y=ax2+bx+c的性质.
复习旧知,导入新课
1.二次函数y=2(x-5)2+6的图象开口方向________,对称轴是________,顶点坐标是(________).它可以由函数y=2x2的图象怎样平移得到的?
2.二次函数
你能很容易地
说出它的图象的对称轴和顶点坐标吗?
X=5
向上
5 , 6
探究新知
活动1:如何确定抛物线
的开口方向、对称轴和顶点坐标
(x - 6) -18+ 21
2
=
= (x2 - 12x ) + 21
= (x2 - 12x + 36 - 36 )+ 21
探究新知
提取二次项系数
配方:加上再减去一次项系数一半的平方
整理:前三项化为完全平方式,后两项合并同类项
化简
(x - 6) + 3
2
=
探究新知
的开口方向、对称轴和顶点坐
标分别是什么?它可由二次函数y=
1.
经过
怎样平移得到的?
(x - 6) + 3
2
=
2.用描点法画出 的图象?
探究新知
x
···
3
4
5
6
7
8
9
···
···
7.5
5
3.5
3
3.5
5
7.5
···
利用图形对称性列表:
O
y
x
5
10
5
10
20
15
x=6
·
(6,3)
·
(8,5)
·
(4,5)
·
(9,7.5)
观察图象:在对称轴的左右两侧,抛物线从左往右的变化趋势.
当_____时y随x的增大而增大
当_____时y随x的增大而减小
x>6
x<6
(3,7.5)
(x - 6) + 3
2
=
y
由图象可知:
(1)在对称轴左侧,抛物线从左到右下降
(2)在对称轴右侧,抛物线从左到右上升
探究新知
活动2:1.不画出图象,你能直接说出函数y=-x2+2x-3的图象的开口方向、对称轴和顶点坐标吗?
y=-x2+2x-3
=-(x2-2x)-3
=-(x2-2x+1-1)-3
=-(x-1)2-2
2.你能画出函数y=-x2+2x-3的图象(草图),并说明这个函数的增减性。
探究新知
3.这个函数的最大值或最小值与函数图象的开口方向有什么关系?这个值与函数图象的顶点坐标有什么关系?
活动3:1、对于任意一个二次函数y=ax2+bx+c(a≠0),如何确定它的对称轴和顶点坐标?请写出结果。
探究新知
一般地,对于二次函数y=ax?+bx+c,我们可以利用配方化成y=a(x-h)2+k的形式导出它的对称轴和顶点坐标.
y=ax2+bx+c配方,得:
因此,其对称轴是:
顶点是: ,
x=
)
(
探究新知
2、请大家观察二次函数y=ax2+bx+c(a≠0)的图象,在对称轴的左右两侧,y随x的增大有什么变化规律?
探究新知
(1):
如果a>0,当 时,y随x的增大而减小,当
时,y随x的增大而增大.
探究新知
(2):
如果a<0,当 时,y随x
的增大而增大,当 时,
y随x的增大而减小.
当堂训练
1、写出下列抛物线的开口方向、对称轴和顶点坐标.(用顶点公式)
(1)y=3x2+2x;(2)y=-x2-2x ;
(3)y=-2x2+8x-8 (4)y=0.5x2-4x+3
1.开口向上,对称轴是x=-1/3,顶点坐标是(-1/3,-1/3)
2.开口向下,对称轴是x=-1,顶点坐标是(-1,1)
3.开口向下,对称轴是x=2,顶点坐标是(2,0)
4.开口向上,对称轴是x=4,顶点坐标是(4,-5)
2、 二次函数y=ax2+4x+a的最大值是3,则 a=________.
当堂训练
3、求二次函数y=mx2+2mx+3(m>0)的图象的对称轴。
-1
x=-1
4、抛物线y=ax2+2x+c的顶点是(-1,2),则a,c的值分别是多少?
当堂训练
a=1,c=3
5、已知抛物线y=x2-2ax+9的顶点在坐标轴
上,求a的值
a=0或±3
课堂小结
本节课你学到了哪些知识?
同课章节目录
