8.1 中学生的视力情况调查-2021春苏科版九年级数学下册课件(29张ppt)
文档属性
| 名称 | 8.1 中学生的视力情况调查-2021春苏科版九年级数学下册课件(29张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 832.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-20 00:00:00 | ||
图片预览







文档简介
第8章 统计和概率的简单应用
8.1 中学生的视力情况调查
1
简单随机抽样
2
用样本估计总体
CONTENTS
1
新知导入
情境引入
环境检测中心为了了解一个城市的空气质量情况,会在这个城市中分散地选择几个点,从各地采集数据.这个例子是普查还是抽样调查,如是抽样调查是否具有代表性,这几个点怎样选取才能具有代表性?
我们这节课来学习样本选取的一种方法——简单的随机抽样.
CONTENTS
2
课程讲授
简单随机抽样
问题1 在现在中学生家庭中,拥有电脑的家庭越来越多,许多同学将电脑用于学习方面,但也有部分同学沉迷于电脑游戏、上网聊天.小丽在网上对中学生上网情况进行调查,结果显示上网查资料的中学生占到99%,而用电脑玩游戏、聊天的人仅占1%,说说你对调查结果的看法.
简单随机抽样
问题2 为了对本地区的视力情况进行调查,小明、小丽、小凯等5名同学决定采用抽样调查的方式进行调查.下面是他们的调查结果,请对他们的调查结果进行分析.
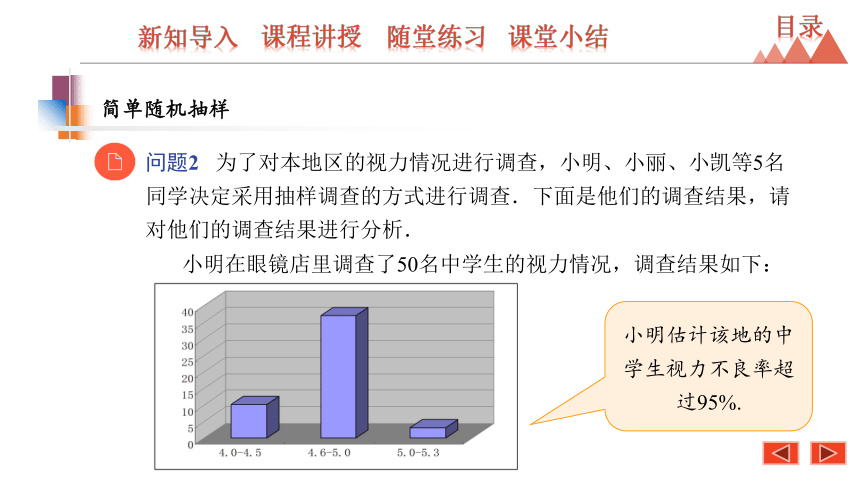
小明在眼镜店里调查了50名中学生的视力情况,调查结果如下:
小明估计该地的中学生视力不良率超过95%.
简单随机抽样
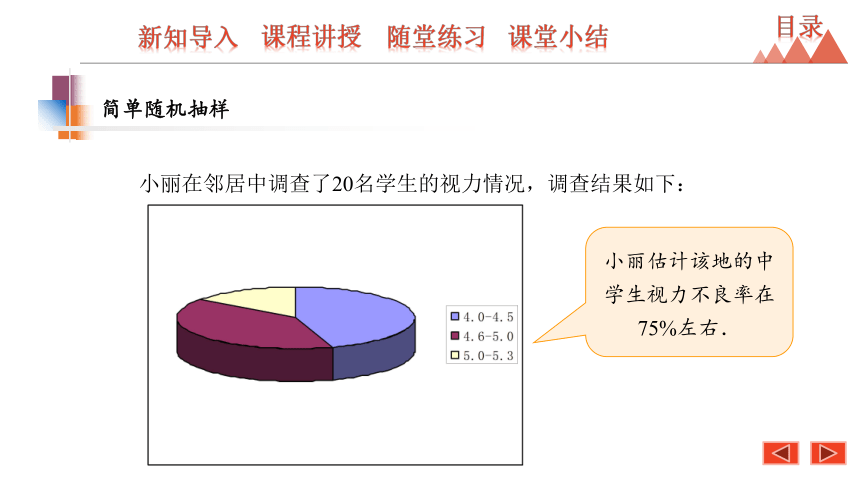
小丽在邻居中调查了20名学生的视力情况,调查结果如下:
小丽估计该地的中学生视力不良率在75%左右.
简单随机抽样
小凯调查了我校每个年级的10名学生,他们的视力情况调查结果
如下:
小凯根据调查结果算得这60名学生的视力不良率为56.7%,由此估计该地的中学生视力不良率接近60%.
小伟查阅了该地区每个中学医务室检查学生的视力资料,并计
算出该地区中学生的视力不良率为65%.
小萍随机调查了该地区的10%的中学生的视力,并计算出他们
的视力不良率为68%.
简单随机抽样
小明、小丽、小凯三名同学都对本地区的特殊群体进行调查,所抽取的样本缺乏代表性,对总体的估计偏差较大.
小伟的调查为普查,但工作量,特别是运算量较大;
小萍抽取的样本具有代表性,对总体的估计比较准确.
你对这5名同学的调查方式有何评价?
简单随机抽样
为了使估计、推断更加准确,抽样时要注意样本的代表性.
简单随机抽样
定 义:
一般地,从个体总数为N的总体中抽取容量为n的样本(n<N),且每次抽取样本时,总体中的每个个体被抽到的可能性相同,这种抽样的方法叫做简单随机抽样.
提示:
在统计里,我们通常是从总体中抽取样本,并根据样本的某种特性估计总体的相应特性.
为了使估计、推断更加准确,抽样时要注意样本的代表性.
要从某校九年级800名学生中抽查50名学生的视力,怎样抽取才能使样本具有代表性?
简单随机抽样
我们可以将这800名学生依次编号(号码从1, 2,…、800),并将号码写在形状、大小、质地都相同的号签上,放人一个盒子中搅匀. 抽签时,每次从中随机抽取一个号签(抽出的号签不放回),号签的号码所对应的个体就人选,连续抽取50次,便得到一个容量为50的样本.
练一练:判断下列抽样调查选取样本的方法是否合适,并说明理由.
(1)为了解某地区老年人的健康状况,在该地区医院里调查了100名老年病人1年内生病的次数;
(2)某方便面厂家为了解产品质量情况,在其生产线上每100包随机抽取1包进行检查;
(3)为了解某城市的空气污染情况,调查了该城市某个月的空气污染情况.
简单随机抽样
解:(1)不合适.因为要了解的是某地区老年人的健康状况,医院里的病人没有代表性.
(2)合适.采取了随机抽样的调查方式,样本具有代表性和广泛性.
(3)不合适.样本缺乏代表性和广泛性.
用样本估计总体
问题3 为了解某市七~九年级学生的视力情况,计划采用抽样调查的方法,从该市2万名七~九年级学生中抽查300名学生的视力,并进行整理分析.考虑到七~九年级学生的视力有较明显的差异,我们采用简单随机抽样的方法从每个年级中各抽查100名学生的视力,整理如下:
为了更方便分析,你认为应该如何处理以上的数据?
用样本估计总体
怎样可以使处理后的数据特点更为直观?
用样本估计总体
用样本估计总体
为从刚才的视力统计表、视力频数分布表和视力频数分布直方图中,你能获得哪些信息?
可以发现,随着年级的升高,所抽查的学生的平均视力在下降,视力不良率在增大…
可以算出,七~九年级
所抽查的学生的视力不良率依次为32%、42%、54.%…
用样本估计总体
例 某市“每天锻炼一小时,幸福生活一辈子”活动已开展了一年,为了解该市此项活动的开展情况,某调查统计公司准备采用以下调查方式中的一种进行调查:
A.从一个社区随机选取200名居民;
B.从一个城镇的不同住宅楼中随机选取200名居民;
C.从该市公安局户籍管理处随机抽取200名城乡居民作为调查对象,然后进行调查.
用样本估计总体
(1)在上述调查方式中,你认为比较合理的一
个是________(填序号);
(2)由一种比较合理的调查方式所得到的数据
制成了如上图所示的频数分布直方图,在
这个调查中,这200名居民每天锻炼2小时
的人数是多少?
(3)若该市有100万人,请你利用(2)中的调查结果,估计该市每天锻炼2小时及以上的人数是多少?
(4)你认为这个调查活动的设计有没有不合理的地方?谈谈你的理由.
用样本估计总体
[解析] (1)要注意样本选择具有广泛的代表性;(2)观察条形图表达的意义;(3)由样本来估计总体情况;(4)注意样本容量要适中,当然只要叙述合理即可.
解:(1)C (2)52人 (3) ×100=53(万人).(4)有不合理的地方.理由:由于全市有100万人,而样本只选取了200人,样本容量较小,不能准确地表达出真实情况.
用样本估计总体
练一练:小芳家今年6月份头6天的用电量如下表:
请你用统计知识,估计小芳家6月份总用电量是( )
A.162 B.120 C.96 D.123
{5940675A-B579-460E-94D1-54222C63F5DA}日期
1日
2日
3日
4日
5日
6日
用电量(度)
3.6
4.8
5.4
4.2
3.4
3.2
D
CONTENTS
3
随堂练习
1.某中学为了解学生的视力情况,需要抽取部分学生进行调查,下列抽取方法中最合适的是( )
A.随机抽取一部分男生
B.随机抽取一个班级的学生
C.随机抽取一个年级的学生
D.在各个年级中,每班随机抽取20名学生
D
2.某大学为了了解法学院1500名新生的身高情况,采用随机调查的方式用300名新生的身高为样本进行统计,其中身高在170cm
~175cm的有75人,那么估计法学院新生身高在170cm~175cm的人数约是( )
A.300 B.325 C.375 D.450
C
3.为了解某初中学校学生的视力情况,需要抽取部分学生进行调查,下列抽取学生的方法最合适的是( )
A.随机抽取该校一个班级的学生
B.随机抽取该校一个年级的学生
C.随机抽取该校一部分男生
D.分别从该校七、八、九年级中各班随机抽取10%的学生
D
4.某养鱼专业户为了估计湖里有多少条鱼,先捕上100条做上标记,然后放回到湖里,过一段时间待带标记的鱼完全混合于鱼群后,再捕上200条鱼,发现其中带标记的鱼有20条,湖里大约有多少条鱼?
解: 设湖里大约有x条鱼,
则 100:x=20:200
∴ x=1000.
答:湖里大约有1000条鱼.
CONTENTS
4
课堂小结
中学生的视力情况调查
简单随机抽样
一般地,从个体总数为N的总体中抽取容量为n的样本(n<N),且每次抽取样本时,总体中的每个个体被抽到的可能性相同,这种抽样的方法叫做简单随机抽样.
用样本估计总体
8.1 中学生的视力情况调查
1
简单随机抽样
2
用样本估计总体
CONTENTS
1
新知导入
情境引入
环境检测中心为了了解一个城市的空气质量情况,会在这个城市中分散地选择几个点,从各地采集数据.这个例子是普查还是抽样调查,如是抽样调查是否具有代表性,这几个点怎样选取才能具有代表性?
我们这节课来学习样本选取的一种方法——简单的随机抽样.
CONTENTS
2
课程讲授
简单随机抽样
问题1 在现在中学生家庭中,拥有电脑的家庭越来越多,许多同学将电脑用于学习方面,但也有部分同学沉迷于电脑游戏、上网聊天.小丽在网上对中学生上网情况进行调查,结果显示上网查资料的中学生占到99%,而用电脑玩游戏、聊天的人仅占1%,说说你对调查结果的看法.
简单随机抽样
问题2 为了对本地区的视力情况进行调查,小明、小丽、小凯等5名同学决定采用抽样调查的方式进行调查.下面是他们的调查结果,请对他们的调查结果进行分析.
小明在眼镜店里调查了50名中学生的视力情况,调查结果如下:
小明估计该地的中学生视力不良率超过95%.
简单随机抽样
小丽在邻居中调查了20名学生的视力情况,调查结果如下:
小丽估计该地的中学生视力不良率在75%左右.
简单随机抽样
小凯调查了我校每个年级的10名学生,他们的视力情况调查结果
如下:
小凯根据调查结果算得这60名学生的视力不良率为56.7%,由此估计该地的中学生视力不良率接近60%.
小伟查阅了该地区每个中学医务室检查学生的视力资料,并计
算出该地区中学生的视力不良率为65%.
小萍随机调查了该地区的10%的中学生的视力,并计算出他们
的视力不良率为68%.
简单随机抽样
小明、小丽、小凯三名同学都对本地区的特殊群体进行调查,所抽取的样本缺乏代表性,对总体的估计偏差较大.
小伟的调查为普查,但工作量,特别是运算量较大;
小萍抽取的样本具有代表性,对总体的估计比较准确.
你对这5名同学的调查方式有何评价?
简单随机抽样
为了使估计、推断更加准确,抽样时要注意样本的代表性.
简单随机抽样
定 义:
一般地,从个体总数为N的总体中抽取容量为n的样本(n<N),且每次抽取样本时,总体中的每个个体被抽到的可能性相同,这种抽样的方法叫做简单随机抽样.
提示:
在统计里,我们通常是从总体中抽取样本,并根据样本的某种特性估计总体的相应特性.
为了使估计、推断更加准确,抽样时要注意样本的代表性.
要从某校九年级800名学生中抽查50名学生的视力,怎样抽取才能使样本具有代表性?
简单随机抽样
我们可以将这800名学生依次编号(号码从1, 2,…、800),并将号码写在形状、大小、质地都相同的号签上,放人一个盒子中搅匀. 抽签时,每次从中随机抽取一个号签(抽出的号签不放回),号签的号码所对应的个体就人选,连续抽取50次,便得到一个容量为50的样本.
练一练:判断下列抽样调查选取样本的方法是否合适,并说明理由.
(1)为了解某地区老年人的健康状况,在该地区医院里调查了100名老年病人1年内生病的次数;
(2)某方便面厂家为了解产品质量情况,在其生产线上每100包随机抽取1包进行检查;
(3)为了解某城市的空气污染情况,调查了该城市某个月的空气污染情况.
简单随机抽样
解:(1)不合适.因为要了解的是某地区老年人的健康状况,医院里的病人没有代表性.
(2)合适.采取了随机抽样的调查方式,样本具有代表性和广泛性.
(3)不合适.样本缺乏代表性和广泛性.
用样本估计总体
问题3 为了解某市七~九年级学生的视力情况,计划采用抽样调查的方法,从该市2万名七~九年级学生中抽查300名学生的视力,并进行整理分析.考虑到七~九年级学生的视力有较明显的差异,我们采用简单随机抽样的方法从每个年级中各抽查100名学生的视力,整理如下:
为了更方便分析,你认为应该如何处理以上的数据?
用样本估计总体
怎样可以使处理后的数据特点更为直观?
用样本估计总体
用样本估计总体
为从刚才的视力统计表、视力频数分布表和视力频数分布直方图中,你能获得哪些信息?
可以发现,随着年级的升高,所抽查的学生的平均视力在下降,视力不良率在增大…
可以算出,七~九年级
所抽查的学生的视力不良率依次为32%、42%、54.%…
用样本估计总体
例 某市“每天锻炼一小时,幸福生活一辈子”活动已开展了一年,为了解该市此项活动的开展情况,某调查统计公司准备采用以下调查方式中的一种进行调查:
A.从一个社区随机选取200名居民;
B.从一个城镇的不同住宅楼中随机选取200名居民;
C.从该市公安局户籍管理处随机抽取200名城乡居民作为调查对象,然后进行调查.
用样本估计总体
(1)在上述调查方式中,你认为比较合理的一
个是________(填序号);
(2)由一种比较合理的调查方式所得到的数据
制成了如上图所示的频数分布直方图,在
这个调查中,这200名居民每天锻炼2小时
的人数是多少?
(3)若该市有100万人,请你利用(2)中的调查结果,估计该市每天锻炼2小时及以上的人数是多少?
(4)你认为这个调查活动的设计有没有不合理的地方?谈谈你的理由.
用样本估计总体
[解析] (1)要注意样本选择具有广泛的代表性;(2)观察条形图表达的意义;(3)由样本来估计总体情况;(4)注意样本容量要适中,当然只要叙述合理即可.
解:(1)C (2)52人 (3) ×100=53(万人).(4)有不合理的地方.理由:由于全市有100万人,而样本只选取了200人,样本容量较小,不能准确地表达出真实情况.
用样本估计总体
练一练:小芳家今年6月份头6天的用电量如下表:
请你用统计知识,估计小芳家6月份总用电量是( )
A.162 B.120 C.96 D.123
{5940675A-B579-460E-94D1-54222C63F5DA}日期
1日
2日
3日
4日
5日
6日
用电量(度)
3.6
4.8
5.4
4.2
3.4
3.2
D
CONTENTS
3
随堂练习
1.某中学为了解学生的视力情况,需要抽取部分学生进行调查,下列抽取方法中最合适的是( )
A.随机抽取一部分男生
B.随机抽取一个班级的学生
C.随机抽取一个年级的学生
D.在各个年级中,每班随机抽取20名学生
D
2.某大学为了了解法学院1500名新生的身高情况,采用随机调查的方式用300名新生的身高为样本进行统计,其中身高在170cm
~175cm的有75人,那么估计法学院新生身高在170cm~175cm的人数约是( )
A.300 B.325 C.375 D.450
C
3.为了解某初中学校学生的视力情况,需要抽取部分学生进行调查,下列抽取学生的方法最合适的是( )
A.随机抽取该校一个班级的学生
B.随机抽取该校一个年级的学生
C.随机抽取该校一部分男生
D.分别从该校七、八、九年级中各班随机抽取10%的学生
D
4.某养鱼专业户为了估计湖里有多少条鱼,先捕上100条做上标记,然后放回到湖里,过一段时间待带标记的鱼完全混合于鱼群后,再捕上200条鱼,发现其中带标记的鱼有20条,湖里大约有多少条鱼?
解: 设湖里大约有x条鱼,
则 100:x=20:200
∴ x=1000.
答:湖里大约有1000条鱼.
CONTENTS
4
课堂小结
中学生的视力情况调查
简单随机抽样
一般地,从个体总数为N的总体中抽取容量为n的样本(n<N),且每次抽取样本时,总体中的每个个体被抽到的可能性相同,这种抽样的方法叫做简单随机抽样.
用样本估计总体
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
