8.3 统计分析帮你做预测-2021春苏科版九年级数学下册课件(16张)
文档属性
| 名称 | 8.3 统计分析帮你做预测-2021春苏科版九年级数学下册课件(16张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 606.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-20 00:00:00 | ||
图片预览





文档简介
第8章 统计和概率的简单应用
8.3 统计分析帮你做预测
1
借助函数模型做预测
CONTENTS
1
新知导入
情境引入
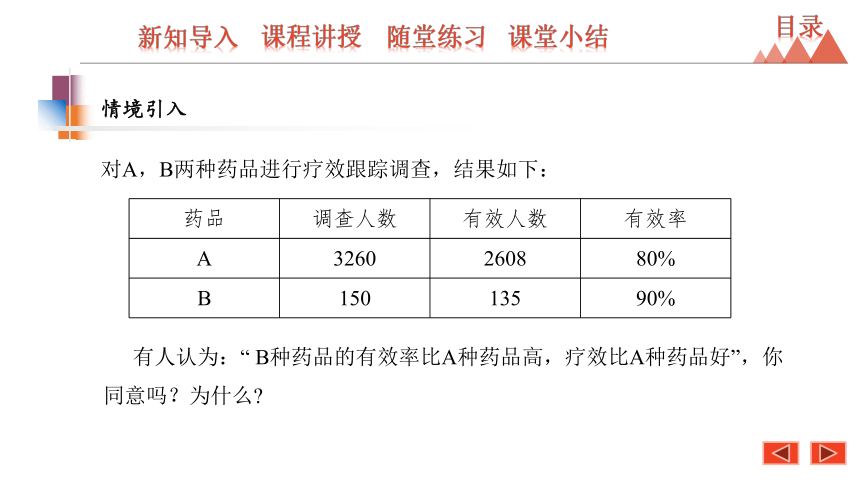
对A,B两种药品进行疗效跟踪调查,结果如下:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}药品
调查人数
有效人数
有效率
A
3260
2608
80%
B
150
135
90%
有人认为:“ B种药品的有效率比A种药品高,疗效比A种药品好”,你同意吗?为什么?
CONTENTS
2
课程讲授
借助函数模型做预测
问题1 我国1992~2004年国内生产总值(GDP)如下:
从表中,你能获得哪些信息?
从表中我们可以看出,我国国内生产总值随年份的增长而不断的增长.
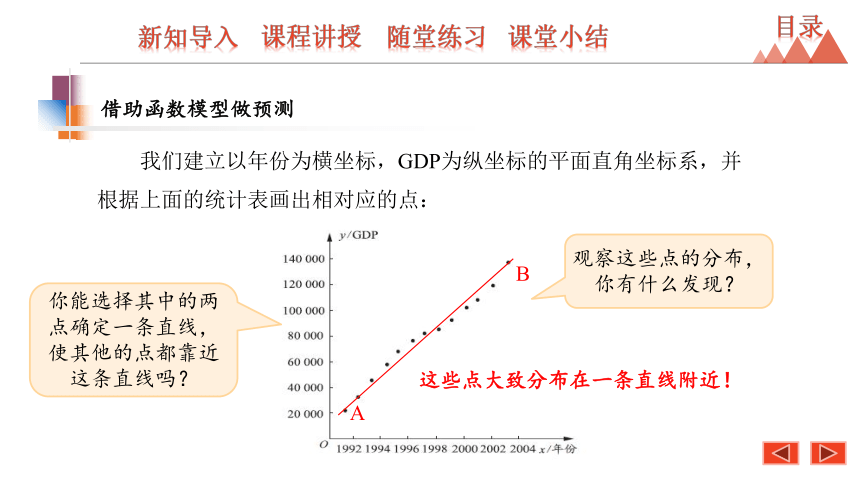
我们建立以年份为横坐标,GDP为纵坐标的平面直角坐标系,并根据上面的统计表画出相对应的点:
借助函数模型做预测
观察这些点的分布,你有什么发现?
这些点大致分布在一条直线附近!
你能选择其中的两点确定一条直线,使其他的点都靠近这条直线吗?
B
A
借助函数模型做预测
你能由此表达式估计我国2004年以后的GDP情况吗?
设直线AB上点的坐标满足函数表达式y=kx+b.由直线AB过点(1992,23 938)、(2004,136 876),可得方程组:
解得k=9 411.5,b=-18 723 770.
所以1992~2004年我国GDP与年份之间的关系可以近似地用函数表达式y=9 411.5x-18 723 770表示.
借助函数模型做预测
问题2 在刚才的问题中,还可以选用其他的直线来近似的表示我国1992~2004年GDP随年份变化而变化的大致发展趋势吗?
可选取点C(1 993,34 634) ,点D(2 003,117 390)所在的直线CD来近似地表示我国1992~2004年GDP不断增长的变化趋势.
借助函数模型分析数据的步骤:
(1)制作统计表;
(2)建立平面直角坐标系:选择事件中的两个量分别作为横坐标、纵坐标建立平面直角坐标系;
(3)描点:根据统计表描出相对应的点;
(4)连线:用光滑的直线或曲线作出图像;
(5)根据图像探究两个量存在的函数关系;
(6)用待定系数法求出函数表达式;
(7)根据函数表达式预测事件的发展趋势.
借助函数模型做预测
CONTENTS
3
随堂练习
我国 1949~1999年间部分年份的人口数据如下:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}年份
1949
1954
1959
1964
1969
1974
1979
1984
1989
1994
1999
人口数/
百万
542
603
672
705
807
909
975
1035
1107
1177
1246
(1) 以年份为横坐标,人口数为纵坐标,在平面直角坐标系中画出相对应的点,并选用一条适当的直线近似表示我国1949~ 1999年间部分年份的人口数与年份之间的变化趋势;
(2)求我国1949~1999年间部分年份的人口数与年份之间关系的近
似表达式,并由这个表达式估计我国2004年的人口数.
解:(1)如图所示,选用直线AB近似表示我国1949~ 1999年间部分年份的人口数与年份之间的变化趋势.
(2)设直线AB上点的坐标满足函数表达式y=kx+b.由直线AB过点(1949,542)、(1999,1246),可得方程组:
解得k=14.08,b=-26 899.92.
所以我国1949~1999年间部分年份的人口数与年份之间的关系的近似表达式为y=14.08x-26 899.92.
当x=2004时, y=14.08×2004-26 899.92 ≈ 1316.所以我国2004年人口约为1316百万人.
CONTENTS
4
课堂小结
反思与小结
在日常生活中,我们经常需要对一些时间的发展趋势做出预测和判断,这个时候我们通过对收集到的数据进行处理、分析,探索其中存在的某种数量关系,并用函数表达式表示出来,借助这一函数表达式对该事件的变化情况做出预测和判断.
在统计分析中,通过画出两个量之间关系的图像,进而求出两个量之间关系的近似函数表达式,借助函数表达式来预测某种结果.
通过这节课的学习你有哪些想法和收获?
8.3 统计分析帮你做预测
1
借助函数模型做预测
CONTENTS
1
新知导入
情境引入
对A,B两种药品进行疗效跟踪调查,结果如下:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}药品
调查人数
有效人数
有效率
A
3260
2608
80%
B
150
135
90%
有人认为:“ B种药品的有效率比A种药品高,疗效比A种药品好”,你同意吗?为什么?
CONTENTS
2
课程讲授
借助函数模型做预测
问题1 我国1992~2004年国内生产总值(GDP)如下:
从表中,你能获得哪些信息?
从表中我们可以看出,我国国内生产总值随年份的增长而不断的增长.
我们建立以年份为横坐标,GDP为纵坐标的平面直角坐标系,并根据上面的统计表画出相对应的点:
借助函数模型做预测
观察这些点的分布,你有什么发现?
这些点大致分布在一条直线附近!
你能选择其中的两点确定一条直线,使其他的点都靠近这条直线吗?
B
A
借助函数模型做预测
你能由此表达式估计我国2004年以后的GDP情况吗?
设直线AB上点的坐标满足函数表达式y=kx+b.由直线AB过点(1992,23 938)、(2004,136 876),可得方程组:
解得k=9 411.5,b=-18 723 770.
所以1992~2004年我国GDP与年份之间的关系可以近似地用函数表达式y=9 411.5x-18 723 770表示.
借助函数模型做预测
问题2 在刚才的问题中,还可以选用其他的直线来近似的表示我国1992~2004年GDP随年份变化而变化的大致发展趋势吗?
可选取点C(1 993,34 634) ,点D(2 003,117 390)所在的直线CD来近似地表示我国1992~2004年GDP不断增长的变化趋势.
借助函数模型分析数据的步骤:
(1)制作统计表;
(2)建立平面直角坐标系:选择事件中的两个量分别作为横坐标、纵坐标建立平面直角坐标系;
(3)描点:根据统计表描出相对应的点;
(4)连线:用光滑的直线或曲线作出图像;
(5)根据图像探究两个量存在的函数关系;
(6)用待定系数法求出函数表达式;
(7)根据函数表达式预测事件的发展趋势.
借助函数模型做预测
CONTENTS
3
随堂练习
我国 1949~1999年间部分年份的人口数据如下:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}年份
1949
1954
1959
1964
1969
1974
1979
1984
1989
1994
1999
人口数/
百万
542
603
672
705
807
909
975
1035
1107
1177
1246
(1) 以年份为横坐标,人口数为纵坐标,在平面直角坐标系中画出相对应的点,并选用一条适当的直线近似表示我国1949~ 1999年间部分年份的人口数与年份之间的变化趋势;
(2)求我国1949~1999年间部分年份的人口数与年份之间关系的近
似表达式,并由这个表达式估计我国2004年的人口数.
解:(1)如图所示,选用直线AB近似表示我国1949~ 1999年间部分年份的人口数与年份之间的变化趋势.
(2)设直线AB上点的坐标满足函数表达式y=kx+b.由直线AB过点(1949,542)、(1999,1246),可得方程组:
解得k=14.08,b=-26 899.92.
所以我国1949~1999年间部分年份的人口数与年份之间的关系的近似表达式为y=14.08x-26 899.92.
当x=2004时, y=14.08×2004-26 899.92 ≈ 1316.所以我国2004年人口约为1316百万人.
CONTENTS
4
课堂小结
反思与小结
在日常生活中,我们经常需要对一些时间的发展趋势做出预测和判断,这个时候我们通过对收集到的数据进行处理、分析,探索其中存在的某种数量关系,并用函数表达式表示出来,借助这一函数表达式对该事件的变化情况做出预测和判断.
在统计分析中,通过画出两个量之间关系的图像,进而求出两个量之间关系的近似函数表达式,借助函数表达式来预测某种结果.
通过这节课的学习你有哪些想法和收获?
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
