8.5 概率帮你做估计-2021春苏科版九年级数学下册课件(24张)
文档属性
| 名称 | 8.5 概率帮你做估计-2021春苏科版九年级数学下册课件(24张) |
|
|
| 格式 | pptx | ||
| 文件大小 | 499.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-20 00:00:00 | ||
图片预览






文档简介
第8章 统计和概率的简单应用
8.5 概率帮你做估计
1
频率与概率的关系
2
用频率估计概率
CONTENTS
1
新知导入
情境导入
下图为著名球星詹姆斯,你知道詹姆斯罚球命中率是多少吗?
CONTENTS
2
课程讲授
频率与概率的关系
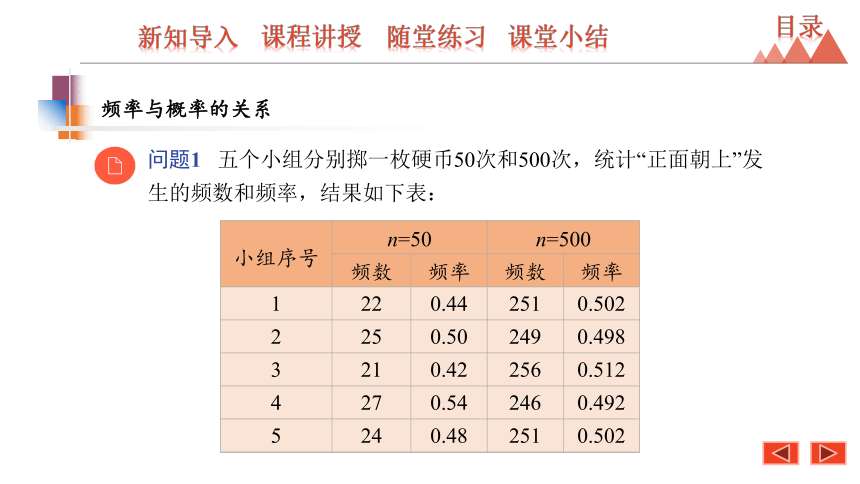
问题1 五个小组分别掷一枚硬币50次和500次,统计“正面朝上”发生的频数和频率,结果如下表:
{5940675A-B579-460E-94D1-54222C63F5DA}小组序号
n=50
n=500
频数
频率
频数
频率
1
22
0.44
251
0.502
2
25
0.50
249
0.498
3
21
0.42
256
0.512
4
27
0.54
246
0.492
5
24
0.48
251
0.502
频率与概率的关系
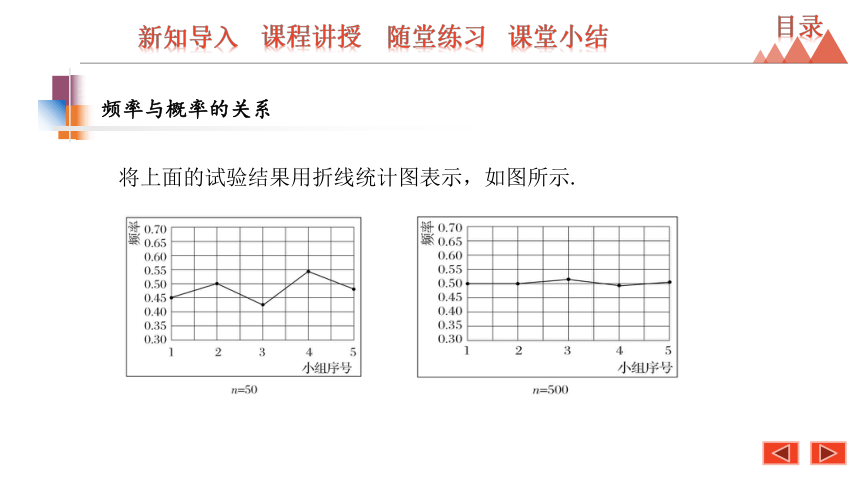
将上面的试验结果用折线统计图表示,如图所示.
频率与概率的关系
想一想:1.当实验次数较小时,频率有什么特征?
2.当实验次数很大时,频率有什么样的变化趋势?
当实验次数较小时,频率不稳定,波动较大
当实验次数很大时,频率会稳定在一个数值附近
频率与概率的关系
归 纳:
对掷硬币试验,“正面朝上”的概率为0.5,而频率则具有不确定性.试验次数不同,频率可能不同;即使是相同次数的不同试验,频率也可能不同.当试验次数较小时,频率的波动较大,但是随着试验次数的增大,“正面朝上”发生的频率波动明显减小,逐渐稳定到0.5附近.这个性质叫做频率的稳定性.
这个数值是什么?
频率与概率的关系
频率与概率的关系
事件发生的概率
O
“正面向上”的概率
抛掷次数n
1
0.5
50
150
250
350
450
频率逐渐稳定
归 纳:
大量试验表明,随着试验次数的增大,事件发生的频率逐渐稳定到它的概率,或者说概率是频率的稳定值.在实际中,我们常用比较稳定时的频率估计事件的概率,而试验次数越大,得到概率的较精确估计值的可能性越大.
频率与概率的关系
频率与概率的关系
练一练:关于频率和概率的关系,下列说法正确的是( )
A.概率等于频率
B.当试验次数很大时,频率稳定在概率附近
C.当试验次数很大时,概率稳定在频率附近
D.试验得到的频率与概率不可能相同
B
用频率估计概率
例 某瓷砖厂在相同条件下抽取部分瓷砖做耐磨试验,结果如下表所示:
则这个厂生产的瓷砖是合格品的概率估计值是______.(精确到0.01)
0.95
提示:运用频率和概率之间的关系,根据频率的波动情况估算概率.
用频率估计概率
归纳:频率估计概率的一般步骤:
①大量重复试验;
②检验频率是否已表现出_______;
③频率的________即为概率.
稳定性
稳定值
用频率估计概率
练一练:在一个不透明的布袋中,红色、黑色、白色的乒乓球共有20个,除颜色外,形状、大小、质地等完全相同,小明通过多次摸球试验后,发现其中摸到红色、黑色球的频率稳定在5%和15%,则口袋中白色球的个数很可能是______个.
16
CONTENTS
3
随堂练习
1.下列说法正确的是( )
A.任意掷一枚质地均匀的硬币10次,一定有5次正面向上
B.天气预报说“明天的降水概率为40%”,表示明天有40%的时间都在降雨
C.“篮球队员在罚球线上投篮一次,投中”为随机事件
D.“a是实数,|a|≥0”是不可能事件
C
2.某人在做掷硬币试验时,投掷m次,正面朝上有n次即正面朝上的频率是P= ,则下列说法中正确的是( )
A.P一定等于
B.P一定不等于
C.多投一次,P更接近
D.投掷次数逐渐增加,P稳定在 附近
D
3.在一个不透明的布袋中,红球、黑球、白球有若干个,除颜色外,形状、大小、质地等完全相同,小新从布袋中随机摸出一个球,记下颜色后放回布袋中,摇匀后再随机摸出一个球,记下颜色如此大量摸球试验后,小新发现其中摸出红球的频率稳定于20%,摸出黑球的频率稳定于50%,对此试验,他总结出下列结论:
①若进行大量摸球试验,摸出白球的频率稳定于30%;
②若从布袋中任意摸出一个球,该球是黑球的概率最大;
③若再摸球100次,必有20次摸出的是红球.
其中说法正确的是( )
A.①②③ B.①② C.①③ D.②③
B
4.在一个不透明的盒子中装有n个球,它们除了颜色之外其他都没有区别,其中含有3个红球,每次摸球前,将盒中所有的球摇匀,然后随机摸出一个球,记下颜色后再放回盒中.通过大量重复试验,发现摸到红球的频率稳定在0.03,那么可以推算出n的值大约是________.
100
5.某地区林业局要考察一种树苗移植的成活率,对该地区这种树苗移植成活情况进行调查统计,并绘制了如图所示的统计表,根据统计图提供的信息解决下列问题:
(1)这种树苗成活的频率稳定在_______,成活的概率估计值为______;
0.9
0.9
(2)该地区已经移植这种树苗5万棵.
①估计这种树苗成活万棵;
②如果该地区计划成活18万棵这种树苗,那么还需移植这种树苗约多少万棵?
∴还需移植这种树苗约15万棵.
解:①估计这种树苗成活4.5万棵
②设还需植x万棵,依题意得
∴x=15,
(x+5)×0.9=18,
CONTENTS
4
课堂小结
概率帮你做估计
频率和概率的关系
用频率估计概率
频率是概率的近似值,概率是频率的稳定值.
步骤:
①大量重复试验;
②检验频率是否已表现出稳定性;
③频率的稳定值即为概率.
8.5 概率帮你做估计
1
频率与概率的关系
2
用频率估计概率
CONTENTS
1
新知导入
情境导入
下图为著名球星詹姆斯,你知道詹姆斯罚球命中率是多少吗?
CONTENTS
2
课程讲授
频率与概率的关系
问题1 五个小组分别掷一枚硬币50次和500次,统计“正面朝上”发生的频数和频率,结果如下表:
{5940675A-B579-460E-94D1-54222C63F5DA}小组序号
n=50
n=500
频数
频率
频数
频率
1
22
0.44
251
0.502
2
25
0.50
249
0.498
3
21
0.42
256
0.512
4
27
0.54
246
0.492
5
24
0.48
251
0.502
频率与概率的关系
将上面的试验结果用折线统计图表示,如图所示.
频率与概率的关系
想一想:1.当实验次数较小时,频率有什么特征?
2.当实验次数很大时,频率有什么样的变化趋势?
当实验次数较小时,频率不稳定,波动较大
当实验次数很大时,频率会稳定在一个数值附近
频率与概率的关系
归 纳:
对掷硬币试验,“正面朝上”的概率为0.5,而频率则具有不确定性.试验次数不同,频率可能不同;即使是相同次数的不同试验,频率也可能不同.当试验次数较小时,频率的波动较大,但是随着试验次数的增大,“正面朝上”发生的频率波动明显减小,逐渐稳定到0.5附近.这个性质叫做频率的稳定性.
这个数值是什么?
频率与概率的关系
频率与概率的关系
事件发生的概率
O
“正面向上”的概率
抛掷次数n
1
0.5
50
150
250
350
450
频率逐渐稳定
归 纳:
大量试验表明,随着试验次数的增大,事件发生的频率逐渐稳定到它的概率,或者说概率是频率的稳定值.在实际中,我们常用比较稳定时的频率估计事件的概率,而试验次数越大,得到概率的较精确估计值的可能性越大.
频率与概率的关系
频率与概率的关系
练一练:关于频率和概率的关系,下列说法正确的是( )
A.概率等于频率
B.当试验次数很大时,频率稳定在概率附近
C.当试验次数很大时,概率稳定在频率附近
D.试验得到的频率与概率不可能相同
B
用频率估计概率
例 某瓷砖厂在相同条件下抽取部分瓷砖做耐磨试验,结果如下表所示:
则这个厂生产的瓷砖是合格品的概率估计值是______.(精确到0.01)
0.95
提示:运用频率和概率之间的关系,根据频率的波动情况估算概率.
用频率估计概率
归纳:频率估计概率的一般步骤:
①大量重复试验;
②检验频率是否已表现出_______;
③频率的________即为概率.
稳定性
稳定值
用频率估计概率
练一练:在一个不透明的布袋中,红色、黑色、白色的乒乓球共有20个,除颜色外,形状、大小、质地等完全相同,小明通过多次摸球试验后,发现其中摸到红色、黑色球的频率稳定在5%和15%,则口袋中白色球的个数很可能是______个.
16
CONTENTS
3
随堂练习
1.下列说法正确的是( )
A.任意掷一枚质地均匀的硬币10次,一定有5次正面向上
B.天气预报说“明天的降水概率为40%”,表示明天有40%的时间都在降雨
C.“篮球队员在罚球线上投篮一次,投中”为随机事件
D.“a是实数,|a|≥0”是不可能事件
C
2.某人在做掷硬币试验时,投掷m次,正面朝上有n次即正面朝上的频率是P= ,则下列说法中正确的是( )
A.P一定等于
B.P一定不等于
C.多投一次,P更接近
D.投掷次数逐渐增加,P稳定在 附近
D
3.在一个不透明的布袋中,红球、黑球、白球有若干个,除颜色外,形状、大小、质地等完全相同,小新从布袋中随机摸出一个球,记下颜色后放回布袋中,摇匀后再随机摸出一个球,记下颜色如此大量摸球试验后,小新发现其中摸出红球的频率稳定于20%,摸出黑球的频率稳定于50%,对此试验,他总结出下列结论:
①若进行大量摸球试验,摸出白球的频率稳定于30%;
②若从布袋中任意摸出一个球,该球是黑球的概率最大;
③若再摸球100次,必有20次摸出的是红球.
其中说法正确的是( )
A.①②③ B.①② C.①③ D.②③
B
4.在一个不透明的盒子中装有n个球,它们除了颜色之外其他都没有区别,其中含有3个红球,每次摸球前,将盒中所有的球摇匀,然后随机摸出一个球,记下颜色后再放回盒中.通过大量重复试验,发现摸到红球的频率稳定在0.03,那么可以推算出n的值大约是________.
100
5.某地区林业局要考察一种树苗移植的成活率,对该地区这种树苗移植成活情况进行调查统计,并绘制了如图所示的统计表,根据统计图提供的信息解决下列问题:
(1)这种树苗成活的频率稳定在_______,成活的概率估计值为______;
0.9
0.9
(2)该地区已经移植这种树苗5万棵.
①估计这种树苗成活万棵;
②如果该地区计划成活18万棵这种树苗,那么还需移植这种树苗约多少万棵?
∴还需移植这种树苗约15万棵.
解:①估计这种树苗成活4.5万棵
②设还需植x万棵,依题意得
∴x=15,
(x+5)×0.9=18,
CONTENTS
4
课堂小结
概率帮你做估计
频率和概率的关系
用频率估计概率
频率是概率的近似值,概率是频率的稳定值.
步骤:
①大量重复试验;
②检验频率是否已表现出稳定性;
③频率的稳定值即为概率.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
