6.3 向心加速度(共18张PPT)
文档属性
| 名称 | 6.3 向心加速度(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-01-21 15:44:33 | ||
图片预览






文档简介
6.3 向心加速度
2020-2021学年度人教版高中物理必修2
第六章 圆周运动
匀速圆周运动向心加速度的方向
F
v
F
v
F
v
做匀速圆周运动的物体,
合外力总是指向圆心
牛顿第二第二定律
做匀速圆周运动时的加速度总指向圆心
向心加速度
关于向心加速度,下列说法正确的是( )
A.?它描述的是角速度变化的快慢
B.?它描述的是线速度大小变化的快慢
C.?在匀速圆周运动中,向心加速度的大小不变
D.?在匀速圆周运动中,向心加速度的方向不变
C
针对练习
讨论:向心加速度的意义
加速度是一个描述速度变化快慢的物理量,但在匀速圆周运动中,速度大小是不变的,那么向心加速度有什么意义?
向心加速度用来描述速度方向变化的快慢
匀速圆周运动中,速度的什么在变?
速度方向即运动方向
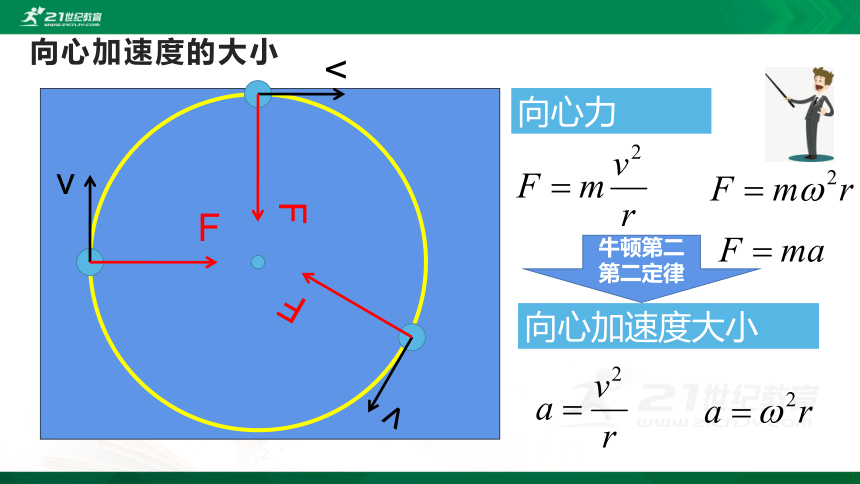
向心加速度的大小
F
v
F
v
F
v
向心力
向心加速度大小
牛顿第二第二定律
有A,B两物体做匀速圆周运动时的向心加速度随半径变化的关系图线如图所示,其中曲线为反比例函数的一部分,则( )
A.?B物体运动时,其线速度的大小不变???
B.?B物体运动时,其角速度不变
C.?A物体运动时,其角速度不变???
D.?A物体运动时,其线速度随r的增大而减小
B
针对练习
如图所示,在长为l 的细绳下端拴一个质量 为 m 的小球,捏住绳子的上端,使小球在水平面内做圆 周运动,细绳就沿圆锥面旋转,这样就成了一个圆锥摆。 当绳子跟竖直方向的夹角为θ 时,小球运动的向心加速 度 an 的大小为多少?通过计算说明:要增大夹角θ,应 该增大小球运动的角速度ω。
解:
根据对小球的受力分析,可得小球的向心力
根据牛顿第二定律可得小球运动的向心加速度
根据几何关系可知小球做圆周运动的半径
把向心加速度公式 an =ω2r和(2)式代入(1)式,可得
从此式可以看出,当小球运动的角速度增大时,夹角也随之增大。因此,要增大夹角θ,应该增大小球运动的角速度ω。
典例分析
3、方向:
2、物理意义:
1、定义:
a=
v2
r
a=rω2
做匀速圆周运动的物体,加速度方向指向圆心,这个加速度叫做向心加速度。
描述速度方向变化的快慢
始终指向圆心
3、方向:
课堂小结
现在很多小区或停车场入口都安装车辆识别系统,当汽车驶近时,道闸杆会自动升起。如图所示,A、B是某道闸杆上不同位置的两点,当道闸杆升起时,A、B两点的角速度大小分别为ωA、ωB,线速度大小分别为vA、vB,向心加速度大小分别为aA、aB,则( )
A.?vA>vB
B.?aA=aB
C.?aAD.?ωA>ωB
A
课堂练习
如图,一轿车以30?m/s的速率沿半径为60?m的圆弧形公路行驶,当轿车从A运动到B时,轿车和圆心的连线转过的角度为90°,求:
(1)此过程中轿车的位移大小;
(2)此过程中轿车通过的路程;
(3)轿车运动的向心加速度大小。
答:(1)此过程中轿车的位移大小为85m;
(2)此过程中轿车通过的路程为94.2m;
(3)轿车运动的向心加速度大小为15m/s2。
课堂练习
扩展:向心加速度的大小推导
情景:已知一个物体做匀速圆周运动,轨迹半径为R,线速度大小为v,求该物体的向心加速度大小?
加速度
定义式
描述速度变化快慢
匀速圆周运动速度方向变化
扩展:向心加速度的大小推导——速度的变化量△V的表示
速度变化量的定义式
V初
O
A
B
V末
△V
V初
知识链接:
向量的平移
向量的相减
扩展:向心加速度的大小推导——速度的变化量△V的大小
已知条件:
由△OAB与△BVAVB相似,有
V初
O
A
B
V末
△V
R
R
v
R
AB
v
=
D
扩展:向心加速度的大小推导——速度的变化量△V的大小
V初
O
A
B
V末
△V
R
R
v
R
AB
v
=
D
当Δt很小时
AB弦长近似等于弧长
扩展:向心加速度的大小推导
V初
O
A
B
V末
△V
R
R
扩展:向心加速度的大小推导
V初
O
A
B
V末
△V
R
R
谢谢聆听
2020-2021学年度人教版高中物理必修2
第六章 圆周运动
匀速圆周运动向心加速度的方向
F
v
F
v
F
v
做匀速圆周运动的物体,
合外力总是指向圆心
牛顿第二第二定律
做匀速圆周运动时的加速度总指向圆心
向心加速度
关于向心加速度,下列说法正确的是( )
A.?它描述的是角速度变化的快慢
B.?它描述的是线速度大小变化的快慢
C.?在匀速圆周运动中,向心加速度的大小不变
D.?在匀速圆周运动中,向心加速度的方向不变
C
针对练习
讨论:向心加速度的意义
加速度是一个描述速度变化快慢的物理量,但在匀速圆周运动中,速度大小是不变的,那么向心加速度有什么意义?
向心加速度用来描述速度方向变化的快慢
匀速圆周运动中,速度的什么在变?
速度方向即运动方向
向心加速度的大小
F
v
F
v
F
v
向心力
向心加速度大小
牛顿第二第二定律
有A,B两物体做匀速圆周运动时的向心加速度随半径变化的关系图线如图所示,其中曲线为反比例函数的一部分,则( )
A.?B物体运动时,其线速度的大小不变???
B.?B物体运动时,其角速度不变
C.?A物体运动时,其角速度不变???
D.?A物体运动时,其线速度随r的增大而减小
B
针对练习
如图所示,在长为l 的细绳下端拴一个质量 为 m 的小球,捏住绳子的上端,使小球在水平面内做圆 周运动,细绳就沿圆锥面旋转,这样就成了一个圆锥摆。 当绳子跟竖直方向的夹角为θ 时,小球运动的向心加速 度 an 的大小为多少?通过计算说明:要增大夹角θ,应 该增大小球运动的角速度ω。
解:
根据对小球的受力分析,可得小球的向心力
根据牛顿第二定律可得小球运动的向心加速度
根据几何关系可知小球做圆周运动的半径
把向心加速度公式 an =ω2r和(2)式代入(1)式,可得
从此式可以看出,当小球运动的角速度增大时,夹角也随之增大。因此,要增大夹角θ,应该增大小球运动的角速度ω。
典例分析
3、方向:
2、物理意义:
1、定义:
a=
v2
r
a=rω2
做匀速圆周运动的物体,加速度方向指向圆心,这个加速度叫做向心加速度。
描述速度方向变化的快慢
始终指向圆心
3、方向:
课堂小结
现在很多小区或停车场入口都安装车辆识别系统,当汽车驶近时,道闸杆会自动升起。如图所示,A、B是某道闸杆上不同位置的两点,当道闸杆升起时,A、B两点的角速度大小分别为ωA、ωB,线速度大小分别为vA、vB,向心加速度大小分别为aA、aB,则( )
A.?vA>vB
B.?aA=aB
C.?aA
A
课堂练习
如图,一轿车以30?m/s的速率沿半径为60?m的圆弧形公路行驶,当轿车从A运动到B时,轿车和圆心的连线转过的角度为90°,求:
(1)此过程中轿车的位移大小;
(2)此过程中轿车通过的路程;
(3)轿车运动的向心加速度大小。
答:(1)此过程中轿车的位移大小为85m;
(2)此过程中轿车通过的路程为94.2m;
(3)轿车运动的向心加速度大小为15m/s2。
课堂练习
扩展:向心加速度的大小推导
情景:已知一个物体做匀速圆周运动,轨迹半径为R,线速度大小为v,求该物体的向心加速度大小?
加速度
定义式
描述速度变化快慢
匀速圆周运动速度方向变化
扩展:向心加速度的大小推导——速度的变化量△V的表示
速度变化量的定义式
V初
O
A
B
V末
△V
V初
知识链接:
向量的平移
向量的相减
扩展:向心加速度的大小推导——速度的变化量△V的大小
已知条件:
由△OAB与△BVAVB相似,有
V初
O
A
B
V末
△V
R
R
v
R
AB
v
=
D
扩展:向心加速度的大小推导——速度的变化量△V的大小
V初
O
A
B
V末
△V
R
R
v
R
AB
v
=
D
当Δt很小时
AB弦长近似等于弧长
扩展:向心加速度的大小推导
V初
O
A
B
V末
△V
R
R
扩展:向心加速度的大小推导
V初
O
A
B
V末
△V
R
R
谢谢聆听
