4.5 多边形和圆的初步认识 课件(共31张PPT)
文档属性
| 名称 | 4.5 多边形和圆的初步认识 课件(共31张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-22 00:00:00 | ||
图片预览











文档简介
第5节 多边形和圆的初步认识
第四章 基本平面图形
2020-2021北师大版七年级数学上册
1.在具体情境中认识多边形和圆,了解与多边形和圆有关的概念.
2.会计算扇形圆心角的度数.
3.经历从现实世界中抽象出平面图形的过程,感受图形世界的丰富
多彩,在丰富的活动中训练发散思维和逻辑思维.
学习目标
1.请观察下面的彩图,抽象出平面图形。你们能从现实生活中“发现”熟悉的平面图形吗?如三角形、四边形、五边形、六边形、圆等。
新课导入
在下列图中找出你熟悉的平面图形。
多边形和圆
知识点一
讲授新课
2.我们经常见到的一些图形:
3.多边形的概念
上面这些图形都是多边形。你能说说他们有什么共同的特征吗?
它们都是由若干条不在同一条直线上的线段首尾顺次相连组成的封闭平面图形。
如果一个多边形由n条线段组成,那么这个多边形叫做n边形.如三角形、四边形、五边形……三角形是最简单的多边形.
其中:各条线段叫多边形的边,相邻两条边的公共端点叫多边形的顶点.
多边形的有关概念:
(1)内角:多边形相邻两边组成的角叫多边形的内角.
(2)外角:多边形的边与它的邻边的延长线组成的角叫做多边形的外角.
下列说法中,正确的有( )个.
(1)三角形是边数最少的多边形;
(2)由n条线段连接起来组成的图形叫多边形;
(3)n边形有n条边、n个顶点、2n个内角和外角;
(4)多边形分为凹多边形和凸多边形.
A.1 B.2 C.3 D.4
针对练习
总结:理解多边形的定义需注意:
(1)线段必须“不在同一直线上”;
(2)必须是“平面图形”;
(3)n为不小于3的正整数.
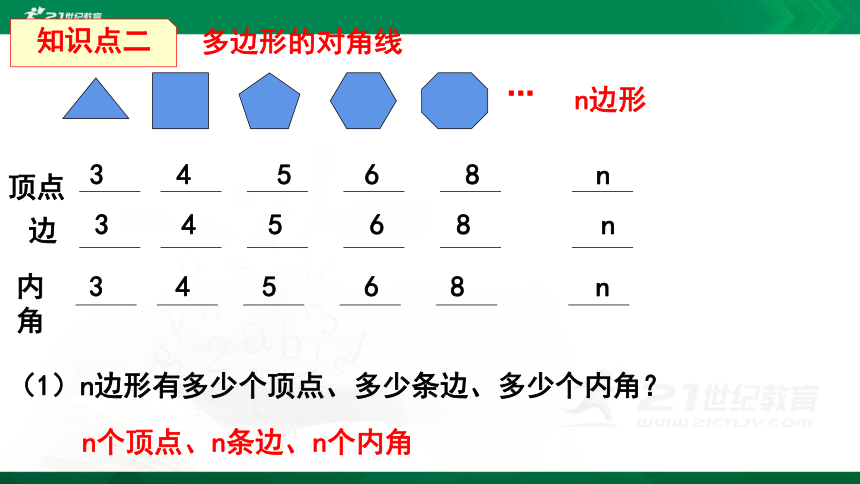
(1)n边形有多少个顶点、多少条边、多少个内角?
n个顶点、n条边、n个内角
顶点
边
内角
n边形
…
3 4 5 6 8 n
3 4 5 6 8 n
3 4 5 6 8 n
多边形的对角线
知识点二
(2)过n边形的每一个顶点有几条对角线?
…
n边形
1
2
3
n-3
边数
对角
线数
n
6
4
5
对角线:
①定义:连接多边形不相邻的两个顶点的线段,叫做多边形的对角线.
②拓展:从n边形的一个顶点出发,可以引(n-3)条对角线,这些对角线把n边形分成(n-2)个三角形;n边形的对角线条数为
(1)四边形从一个顶点可引出几条对角线?共有几条对角线?五边形呢?
(2)n边形从一个顶点可引出几条对角线?共有几条对角线?请说明理由.
针对练习
总结:(1)由“特殊”到“一般”的方法是找规律问题的常用方法.
(2)本题的结论要求会熟练运用:从n边形的一个顶点出发可以作(n-3)条对角线,此时,n边形被分成(n-2)个三角形.一个n边形一共可以作n(n-3)条对角线.
正多边形
知识点三
议一议
观察下图中的多边形,它们的边、角有什么特点?与同伴进行交流.
各边相等,各角也相等的多边形叫做正多边形,所以正多边形同时具有各边相等,各角相等的性质.
下列说法不正确的是( )
A.正多边形的各边都相等
B.各边都相等的多边形是正多边形
C.正三角形就是等边三角形
D.六条边、六个内角都相等的六边形都是正六边形
针对练习
总结:正多边形有两个条件:
(1)各个角都相等,
(2)各条边都相等.
二者缺一不可,若一个多边形的各个角都相等或每条边都相等并不一定是正多边形.
圆及相关概念
知识点四
上面的图形中有我们熟悉的圆和扇形,你还记得用哪些方法可以画一个圆吗?你能用一根细绳和笔画出一个圆吗?
B
A
绳子扫过的区域是什么形状?
议一议
平面上,一条线段绕着它固定的一个端点旋转一周,另一个端点形成的图形叫做圆.固定的端点O称为圆心,线段OA称为半径.圆上A,B两点之间的部分叫做圆弧;
O
·
圆心角:我们把顶点在圆心的角叫做圆心角.
O
B
A
∠AOB为圆心角
圆心角∠AOB所对的弦为AB,所对的弧为AB.
⌒
圆心角、扇形
知识点五
扇形:由组成圆心角的两条半径和圆心角所对的弧所围成的图形叫做扇形.
判别下列各图中的角是不是圆心角,并说明理由.
①
②
③
④
任意给圆心角,对应出现三个量:
圆心角
弧
弦
·
O
B
A
疑问:这三个量之间会有什么关系呢?
归纳:(1)1°的圆心角所对的弧叫做1°的弧.这样,n°的圆心角所对的弧就是n°的弧.
(2)圆心角的度数与它所对的弧的度数是一致(或相等)的,即圆心角的度数等于它所对弧的度数.注意这里仅指度数相等.
下面四个图形中的角,是圆心角的是( )
针对练习
将一个圆分割成三个扇形,它们的圆心角的度数比为1 : 2 : 3,求这三个扇形的圆心角的度数.
总结:圆可以分割成若干个扇形.①扇形的面积比等于各扇形的圆心角的度数比.②扇形的面积公式为S扇形= (扇形圆心角的度数为n°,半径为r,S扇形表示扇形的面积).
针对练习
1.下列图形中,属于多边形的是( )
A.线段 B.角 C.六边形 D.圆
课堂练习
2.下列图形中,是正多边形的是( )
A.等腰三角形
B.长方形
C.正方形
D.五边都相等的五边形
n边形的内角和为(n-2)×180°(n≥3)
n边形从一个顶点出发的对角线有(n-3)条(n≥3)
n边形共有对角线 条(n≥3)
任何多边形的外角和为360°
课堂小结
谢谢聆听
第四章 基本平面图形
2020-2021北师大版七年级数学上册
1.在具体情境中认识多边形和圆,了解与多边形和圆有关的概念.
2.会计算扇形圆心角的度数.
3.经历从现实世界中抽象出平面图形的过程,感受图形世界的丰富
多彩,在丰富的活动中训练发散思维和逻辑思维.
学习目标
1.请观察下面的彩图,抽象出平面图形。你们能从现实生活中“发现”熟悉的平面图形吗?如三角形、四边形、五边形、六边形、圆等。
新课导入
在下列图中找出你熟悉的平面图形。
多边形和圆
知识点一
讲授新课
2.我们经常见到的一些图形:
3.多边形的概念
上面这些图形都是多边形。你能说说他们有什么共同的特征吗?
它们都是由若干条不在同一条直线上的线段首尾顺次相连组成的封闭平面图形。
如果一个多边形由n条线段组成,那么这个多边形叫做n边形.如三角形、四边形、五边形……三角形是最简单的多边形.
其中:各条线段叫多边形的边,相邻两条边的公共端点叫多边形的顶点.
多边形的有关概念:
(1)内角:多边形相邻两边组成的角叫多边形的内角.
(2)外角:多边形的边与它的邻边的延长线组成的角叫做多边形的外角.
下列说法中,正确的有( )个.
(1)三角形是边数最少的多边形;
(2)由n条线段连接起来组成的图形叫多边形;
(3)n边形有n条边、n个顶点、2n个内角和外角;
(4)多边形分为凹多边形和凸多边形.
A.1 B.2 C.3 D.4
针对练习
总结:理解多边形的定义需注意:
(1)线段必须“不在同一直线上”;
(2)必须是“平面图形”;
(3)n为不小于3的正整数.
(1)n边形有多少个顶点、多少条边、多少个内角?
n个顶点、n条边、n个内角
顶点
边
内角
n边形
…
3 4 5 6 8 n
3 4 5 6 8 n
3 4 5 6 8 n
多边形的对角线
知识点二
(2)过n边形的每一个顶点有几条对角线?
…
n边形
1
2
3
n-3
边数
对角
线数
n
6
4
5
对角线:
①定义:连接多边形不相邻的两个顶点的线段,叫做多边形的对角线.
②拓展:从n边形的一个顶点出发,可以引(n-3)条对角线,这些对角线把n边形分成(n-2)个三角形;n边形的对角线条数为
(1)四边形从一个顶点可引出几条对角线?共有几条对角线?五边形呢?
(2)n边形从一个顶点可引出几条对角线?共有几条对角线?请说明理由.
针对练习
总结:(1)由“特殊”到“一般”的方法是找规律问题的常用方法.
(2)本题的结论要求会熟练运用:从n边形的一个顶点出发可以作(n-3)条对角线,此时,n边形被分成(n-2)个三角形.一个n边形一共可以作n(n-3)条对角线.
正多边形
知识点三
议一议
观察下图中的多边形,它们的边、角有什么特点?与同伴进行交流.
各边相等,各角也相等的多边形叫做正多边形,所以正多边形同时具有各边相等,各角相等的性质.
下列说法不正确的是( )
A.正多边形的各边都相等
B.各边都相等的多边形是正多边形
C.正三角形就是等边三角形
D.六条边、六个内角都相等的六边形都是正六边形
针对练习
总结:正多边形有两个条件:
(1)各个角都相等,
(2)各条边都相等.
二者缺一不可,若一个多边形的各个角都相等或每条边都相等并不一定是正多边形.
圆及相关概念
知识点四
上面的图形中有我们熟悉的圆和扇形,你还记得用哪些方法可以画一个圆吗?你能用一根细绳和笔画出一个圆吗?
B
A
绳子扫过的区域是什么形状?
议一议
平面上,一条线段绕着它固定的一个端点旋转一周,另一个端点形成的图形叫做圆.固定的端点O称为圆心,线段OA称为半径.圆上A,B两点之间的部分叫做圆弧;
O
·
圆心角:我们把顶点在圆心的角叫做圆心角.
O
B
A
∠AOB为圆心角
圆心角∠AOB所对的弦为AB,所对的弧为AB.
⌒
圆心角、扇形
知识点五
扇形:由组成圆心角的两条半径和圆心角所对的弧所围成的图形叫做扇形.
判别下列各图中的角是不是圆心角,并说明理由.
①
②
③
④
任意给圆心角,对应出现三个量:
圆心角
弧
弦
·
O
B
A
疑问:这三个量之间会有什么关系呢?
归纳:(1)1°的圆心角所对的弧叫做1°的弧.这样,n°的圆心角所对的弧就是n°的弧.
(2)圆心角的度数与它所对的弧的度数是一致(或相等)的,即圆心角的度数等于它所对弧的度数.注意这里仅指度数相等.
下面四个图形中的角,是圆心角的是( )
针对练习
将一个圆分割成三个扇形,它们的圆心角的度数比为1 : 2 : 3,求这三个扇形的圆心角的度数.
总结:圆可以分割成若干个扇形.①扇形的面积比等于各扇形的圆心角的度数比.②扇形的面积公式为S扇形= (扇形圆心角的度数为n°,半径为r,S扇形表示扇形的面积).
针对练习
1.下列图形中,属于多边形的是( )
A.线段 B.角 C.六边形 D.圆
课堂练习
2.下列图形中,是正多边形的是( )
A.等腰三角形
B.长方形
C.正方形
D.五边都相等的五边形
n边形的内角和为(n-2)×180°(n≥3)
n边形从一个顶点出发的对角线有(n-3)条(n≥3)
n边形共有对角线 条(n≥3)
任何多边形的外角和为360°
课堂小结
谢谢聆听
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
