人教版七年级上册4.2 线段长短的比较课件(28张ppt)
文档属性
| 名称 | 人教版七年级上册4.2 线段长短的比较课件(28张ppt) |
|
|
| 格式 | zip | ||
| 文件大小 | 324.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-21 07:50:51 | ||
图片预览






文档简介
(共28张PPT)
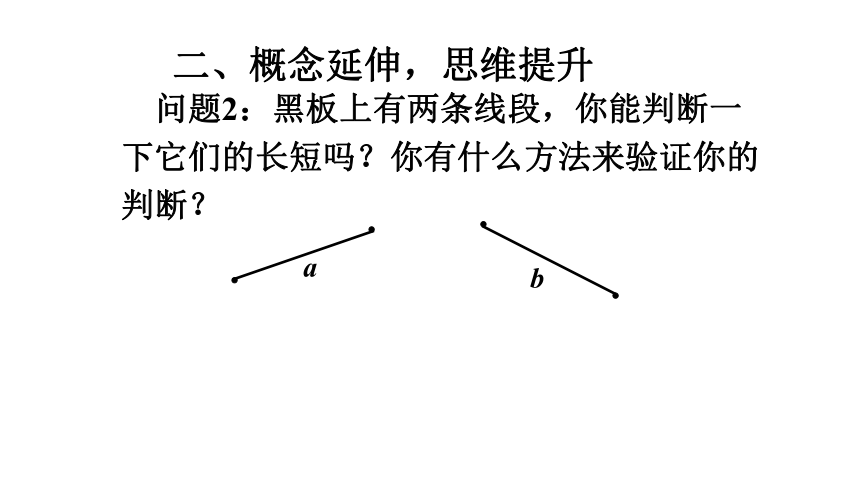
直线、射线、线段的联系与区别.
回顾旧知
名称
图形
表示
延伸
端点
度量
直线
1.直线AB
(或直线BA)
2.直线l
向两端无限延伸
0个
不可度量
射线
1.射线AB
2.射线l
向一端无限延伸
1个
不可度量
线段
1.线段AB
(或线段BA)
2.线段a
不可延伸
2个
可度量
B
·
l
A
·
B
·
l
A
·
B
·
a
A
·
1.直线AB
(或直线BA)
2.直线l
向两端无限延伸
0个
不可度量
1.射线AB
2.射线l
向一端无限延伸
1个
不可度量
1.线段AB
(或线段BA)
2.线段a
不可延伸
2个
可度量
一、开门见山,引入新知
问题1:老师手里的纸上有一条线段,你能在你的本上作出一条同样大小的线段来吗?
a
二、概念延伸,思维提升
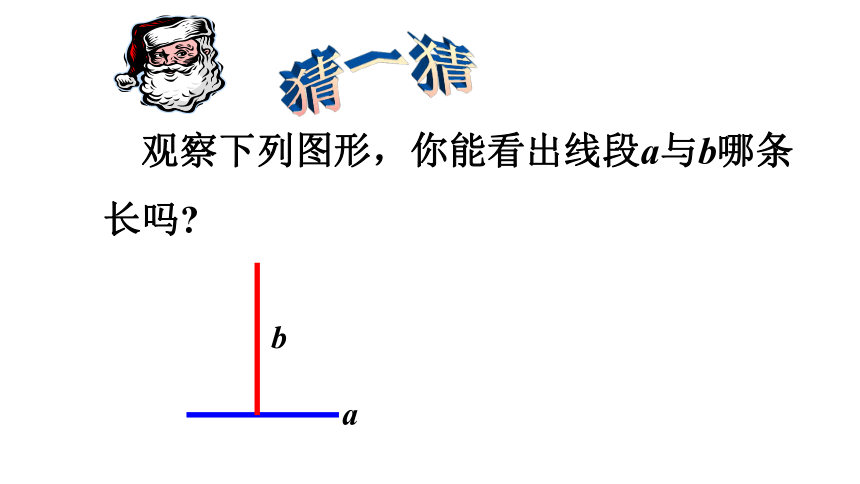
问题2:黑板上有两条线段,你能判断一下它们的长短吗?你有什么方法来验证你的判断?
a
b
4.2
线段长短的比较
观察下列图形,你能看出线段a与b哪条长吗?
猜一猜
a
b
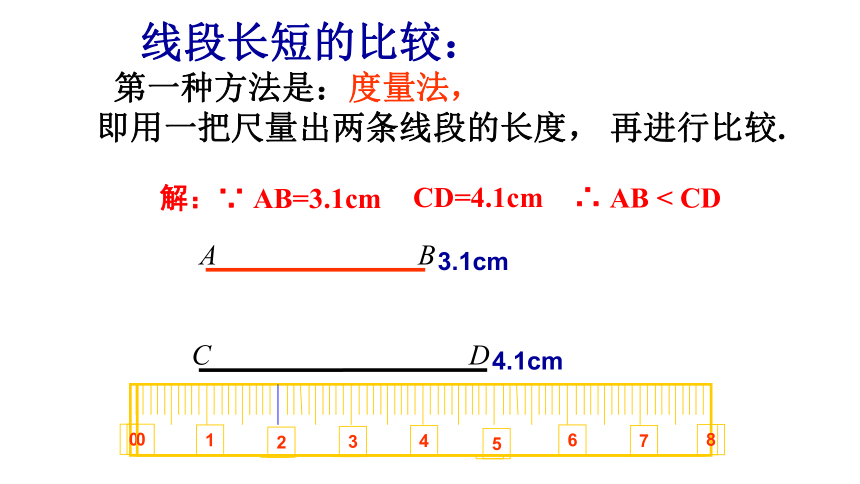
第一种方法是:度量法,
即用一把尺量出两条线段的长度,
再进行比较.
1
2
3
5
4
6
7
8
0
3.1cm
4.1cm
1
2
3
5
4
6
7
8
0
线段长短的比较:
A
B
C
D
解:∵
AB=3.1cm
CD=4.1cm
∴
AB
<
CD
讨论:
你们平时是如何比较两个同学的身高的?你能从比身高的方法中得到启示来比较两条线段的长短吗?说说你们的想法.
叠合法比较线段的长短:
将线段AB放到CD上,使点A与点C重合,点B和点D在重合点的同侧.
A
B
C
D
A
B
C
D
则AB=CD
(1)若点B和点D重合
则AB(2)若点B在线段CD上
A
B
C
D
则AB>CD
(3)若点B在线段CD外
比较线段长短的两种方法
1、度量法——从“数值”的角度比较
2、叠合法——从“形”的角度比较
起点对齐,看终点
A
C
1
2
3
4
D
小黄该走哪条路线呢?
A
B
线段的性质:
两点之间的所有连线中,线段最短.
也可简述为:“两点之间,线段最短”.
两点的距离:连接两点间的线段的长度.
①作射线AM;
线段AB为所求的线段.
已知线段a,作线段AB,使线段AB=a.
②在射线AM上截取AB=
a
.
问题探究1
(1)怎样画一条线段等于已知线段?
作法:
已知:线段a,b(如图),用直尺和圆规画一条线段c,使得它的长度等于两条已知线段的长度的和.
a
b
画法:
1、画射线OP;
2、用圆规在射线OP上截取OA=a
;
3、用圆规在射线AP上截取AC=b.
∴线段OC就是所求的线段c.
O
P
A
画一画
C
线段c的长度是线段a,b的长度的和,我们就说线段c是线段a,b的和,记做c=a+b;
一看起点,二看方向,
三看落点.
a
1、你能用直尺和圆规画出一条线段c,使它等于已知线段a的2倍.
尺规作图注意事项:
1、只要求作出图形,说明结果;
2、保留作图痕迹.
请说说你的画法
O
P
B
线段OB就是所求做的线段c.
画一画
A
直尺只用来画线,不用来量距离;
已知线段a,b(如图),用直尺和圆规画一条
线段d,使它的长度等于a-b.
a
b
合作探究:
你会画吗?画法如何?
团结就是力量
画法:
1、画射线OP;
2、用圆规截取OA=a;
O
P
A
3、用圆规截取AB=b;
B
线段OB就是所求做的线段d=a-b.
一看起点,二看方向,三看落点.
已知线段a,b,画一条线段c,使它的长度等于3a-b
(利用直尺和圆规).
a
b
画法:
1.画射线AF.
2.用圆规在射线AF上依次截取AB=BC=CD=a.
3.
在线段AD上截取DE=b.
线段AE就是所求的线段c.
A
F
B
C
D
a
a
a
E
b
D
(或线段AE=3a-b)
试一试
填一填
如图,填空:
A
B
C
D
AB+BC=_____
AC
AD
-
CD=_____
AC
BC=_____
-
CD
BD
AD=____
+
____
+
____
AB
BC
CD
动手操作
在一张透明的纸上画一条线段AB,折叠纸片,使端点A、B
重合,折痕与线段的交点记为点M,此时有几条线段?
它们之间有什么样的关系?
问题探究2
1.
线段中点:把一条线段分成相等两部分
的点叫线段的中点.
问题探究2
M
A
B
(如图:M是线段AB的中点)
如何用符号语言表示?
则(1)AM=BM
(3)AB=2AM=2BM.
(2)AM=BM=
2.线段的三等分点:
3.线段的四等分点:
A
B
M
N
A
B
M
N
P
(1)
如图,线段AB=18cm,点C是线段AB的中点,点D在线段CB上,且CD=3cm,则线段AD=_______.
12cm
小试牛刀
9cm
3cm
(2)
如图,点C是线段AB的中点,那么
①AB=2AC;
②2BC=AB;
③AC=BC;
④AC+BC=AB.
上述四个式子中,正确的有(
)
A
.
1个
B.
2个
C.
3个
D.
4个
小试牛刀
C
A
B
D
(3)如图,下列说法不能判断点C是线段AB的中点的是
(
)
A.
AC=CB
B.
AB=2AC
C.
AC+CB=AB
D.
CB=
AB
C
C
A
B
(4)已知:直线
l
上有A、B、C三点,
且线段AB=8cm,线段BC=5cm,求线
段AC的长.
解:(1)如图:
(2)如图:
AC=AB+BC
=8+5=13cm
AC=AB-BC
=8-5=3cm
l
A
B
C
l
A
B
C
已知线段AB=10,点C在直线AB上,且AC=4,若点D是AB的中点,求DC的长.
情况一:点C在点A的左侧
情况二:点C在点A的右侧
思维拓展
一、学习了怎样比较线段的长短:
1、度量法:
2、叠合法:起点对齐,看终点.
本节课你又增长了哪些知识?
谈谈收获吧
二、尺规作图
1、用尺规法画一条线段等于已知线段;
2、用尺规法画已知线段的和与差.
一看起点,二看方向
三看落点.
画一条线段等于已知线段
线段比较大小
线段的和、差、分点(中点、三等分点等)
两点之间线段最短
两点的距离定义
公元前五世纪的希腊数学家,已经习惯于用不带刻度的直尺和圆规(以下简称尺规)来作图了。在他们看来,直线和圆是可以信赖的最基本的图形,而直尺和圆规是这两种图形的具体体现,因而只有用尺规作出的图形才是可信的。于是他们热衷于在尺规限制下探讨几何作图问题。数学家们总是对用简单的工具解决困难的问题备加赞赏,自然对用尺规去画各种图形饶有兴趣。尺规作图是对人类智慧的挑战,是培养人的思维与操作能力的有效手段。
数学小趣闻—尺规作图
直线、射线、线段的联系与区别.
回顾旧知
名称
图形
表示
延伸
端点
度量
直线
1.直线AB
(或直线BA)
2.直线l
向两端无限延伸
0个
不可度量
射线
1.射线AB
2.射线l
向一端无限延伸
1个
不可度量
线段
1.线段AB
(或线段BA)
2.线段a
不可延伸
2个
可度量
B
·
l
A
·
B
·
l
A
·
B
·
a
A
·
1.直线AB
(或直线BA)
2.直线l
向两端无限延伸
0个
不可度量
1.射线AB
2.射线l
向一端无限延伸
1个
不可度量
1.线段AB
(或线段BA)
2.线段a
不可延伸
2个
可度量
一、开门见山,引入新知
问题1:老师手里的纸上有一条线段,你能在你的本上作出一条同样大小的线段来吗?
a
二、概念延伸,思维提升
问题2:黑板上有两条线段,你能判断一下它们的长短吗?你有什么方法来验证你的判断?
a
b
4.2
线段长短的比较
观察下列图形,你能看出线段a与b哪条长吗?
猜一猜
a
b
第一种方法是:度量法,
即用一把尺量出两条线段的长度,
再进行比较.
1
2
3
5
4
6
7
8
0
3.1cm
4.1cm
1
2
3
5
4
6
7
8
0
线段长短的比较:
A
B
C
D
解:∵
AB=3.1cm
CD=4.1cm
∴
AB
<
CD
讨论:
你们平时是如何比较两个同学的身高的?你能从比身高的方法中得到启示来比较两条线段的长短吗?说说你们的想法.
叠合法比较线段的长短:
将线段AB放到CD上,使点A与点C重合,点B和点D在重合点的同侧.
A
B
C
D
A
B
C
D
则AB=CD
(1)若点B和点D重合
则AB
A
B
C
D
则AB>CD
(3)若点B在线段CD外
比较线段长短的两种方法
1、度量法——从“数值”的角度比较
2、叠合法——从“形”的角度比较
起点对齐,看终点
A
C
1
2
3
4
D
小黄该走哪条路线呢?
A
B
线段的性质:
两点之间的所有连线中,线段最短.
也可简述为:“两点之间,线段最短”.
两点的距离:连接两点间的线段的长度.
①作射线AM;
线段AB为所求的线段.
已知线段a,作线段AB,使线段AB=a.
②在射线AM上截取AB=
a
.
问题探究1
(1)怎样画一条线段等于已知线段?
作法:
已知:线段a,b(如图),用直尺和圆规画一条线段c,使得它的长度等于两条已知线段的长度的和.
a
b
画法:
1、画射线OP;
2、用圆规在射线OP上截取OA=a
;
3、用圆规在射线AP上截取AC=b.
∴线段OC就是所求的线段c.
O
P
A
画一画
C
线段c的长度是线段a,b的长度的和,我们就说线段c是线段a,b的和,记做c=a+b;
一看起点,二看方向,
三看落点.
a
1、你能用直尺和圆规画出一条线段c,使它等于已知线段a的2倍.
尺规作图注意事项:
1、只要求作出图形,说明结果;
2、保留作图痕迹.
请说说你的画法
O
P
B
线段OB就是所求做的线段c.
画一画
A
直尺只用来画线,不用来量距离;
已知线段a,b(如图),用直尺和圆规画一条
线段d,使它的长度等于a-b.
a
b
合作探究:
你会画吗?画法如何?
团结就是力量
画法:
1、画射线OP;
2、用圆规截取OA=a;
O
P
A
3、用圆规截取AB=b;
B
线段OB就是所求做的线段d=a-b.
一看起点,二看方向,三看落点.
已知线段a,b,画一条线段c,使它的长度等于3a-b
(利用直尺和圆规).
a
b
画法:
1.画射线AF.
2.用圆规在射线AF上依次截取AB=BC=CD=a.
3.
在线段AD上截取DE=b.
线段AE就是所求的线段c.
A
F
B
C
D
a
a
a
E
b
D
(或线段AE=3a-b)
试一试
填一填
如图,填空:
A
B
C
D
AB+BC=_____
AC
AD
-
CD=_____
AC
BC=_____
-
CD
BD
AD=____
+
____
+
____
AB
BC
CD
动手操作
在一张透明的纸上画一条线段AB,折叠纸片,使端点A、B
重合,折痕与线段的交点记为点M,此时有几条线段?
它们之间有什么样的关系?
问题探究2
1.
线段中点:把一条线段分成相等两部分
的点叫线段的中点.
问题探究2
M
A
B
(如图:M是线段AB的中点)
如何用符号语言表示?
则(1)AM=BM
(3)AB=2AM=2BM.
(2)AM=BM=
2.线段的三等分点:
3.线段的四等分点:
A
B
M
N
A
B
M
N
P
(1)
如图,线段AB=18cm,点C是线段AB的中点,点D在线段CB上,且CD=3cm,则线段AD=_______.
12cm
小试牛刀
9cm
3cm
(2)
如图,点C是线段AB的中点,那么
①AB=2AC;
②2BC=AB;
③AC=BC;
④AC+BC=AB.
上述四个式子中,正确的有(
)
A
.
1个
B.
2个
C.
3个
D.
4个
小试牛刀
C
A
B
D
(3)如图,下列说法不能判断点C是线段AB的中点的是
(
)
A.
AC=CB
B.
AB=2AC
C.
AC+CB=AB
D.
CB=
AB
C
C
A
B
(4)已知:直线
l
上有A、B、C三点,
且线段AB=8cm,线段BC=5cm,求线
段AC的长.
解:(1)如图:
(2)如图:
AC=AB+BC
=8+5=13cm
AC=AB-BC
=8-5=3cm
l
A
B
C
l
A
B
C
已知线段AB=10,点C在直线AB上,且AC=4,若点D是AB的中点,求DC的长.
情况一:点C在点A的左侧
情况二:点C在点A的右侧
思维拓展
一、学习了怎样比较线段的长短:
1、度量法:
2、叠合法:起点对齐,看终点.
本节课你又增长了哪些知识?
谈谈收获吧
二、尺规作图
1、用尺规法画一条线段等于已知线段;
2、用尺规法画已知线段的和与差.
一看起点,二看方向
三看落点.
画一条线段等于已知线段
线段比较大小
线段的和、差、分点(中点、三等分点等)
两点之间线段最短
两点的距离定义
公元前五世纪的希腊数学家,已经习惯于用不带刻度的直尺和圆规(以下简称尺规)来作图了。在他们看来,直线和圆是可以信赖的最基本的图形,而直尺和圆规是这两种图形的具体体现,因而只有用尺规作出的图形才是可信的。于是他们热衷于在尺规限制下探讨几何作图问题。数学家们总是对用简单的工具解决困难的问题备加赞赏,自然对用尺规去画各种图形饶有兴趣。尺规作图是对人类智慧的挑战,是培养人的思维与操作能力的有效手段。
数学小趣闻—尺规作图
