中考数学几何模型:费马点最值模型(Word版,附答案)
文档属性
| 名称 | 中考数学几何模型:费马点最值模型(Word版,附答案) |  | |
| 格式 | zip | ||
| 文件大小 | 625.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-20 23:19:16 | ||
图片预览



文档简介
中考数学几何模型:费马点最值模型
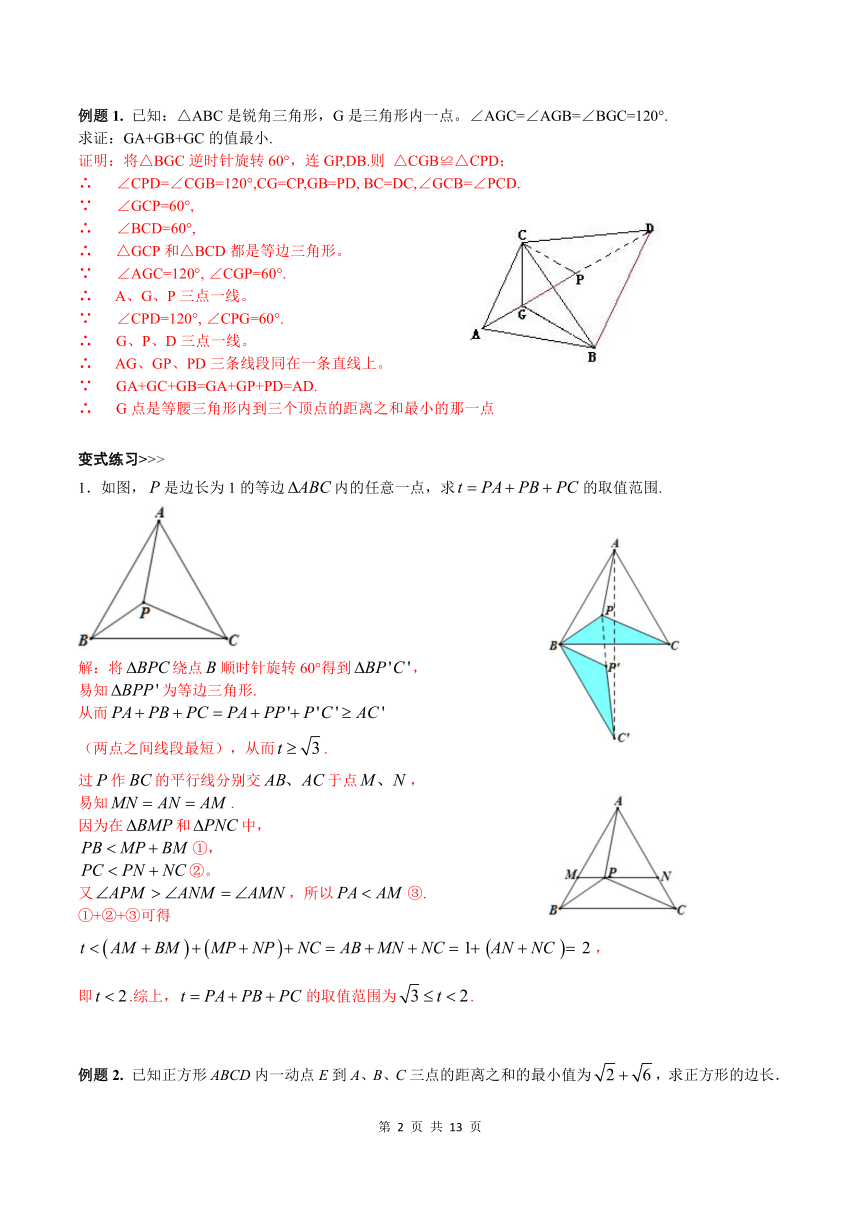
费马尔问题思考:
如何找一点P使它到△ABC三个顶点的距离之和PA+PB+PC最小?
当B、P、Q、E四点共线时取得最小值
费马点的定义:数学上称,到三角形3个顶点距离之和最小的点为费马点。
它是这样确定的:
1.
如果三角形有一个内角大于或等于120°,这个内角的顶点就是费马点;
2.
如果3个内角均小于120°,则在三角形内部对3边张角均为120°的点,是三角形的费马点。
费马点的性质:费马点有如下主要性质:
1.费马点到三角形三个顶点距离之和最小。
2.费马点连接三顶点所成的三夹角皆为120°。
费马点最小值快速求解:
费尔马问题告诉我们,存在这么一个点到三个定点的距离的和最小,解决问题的方法是运用旋转变换.
秘诀:以△ABC任意一边为边向外作等边三角形,这条边所对两顶点的距离即为最小值
典题探究
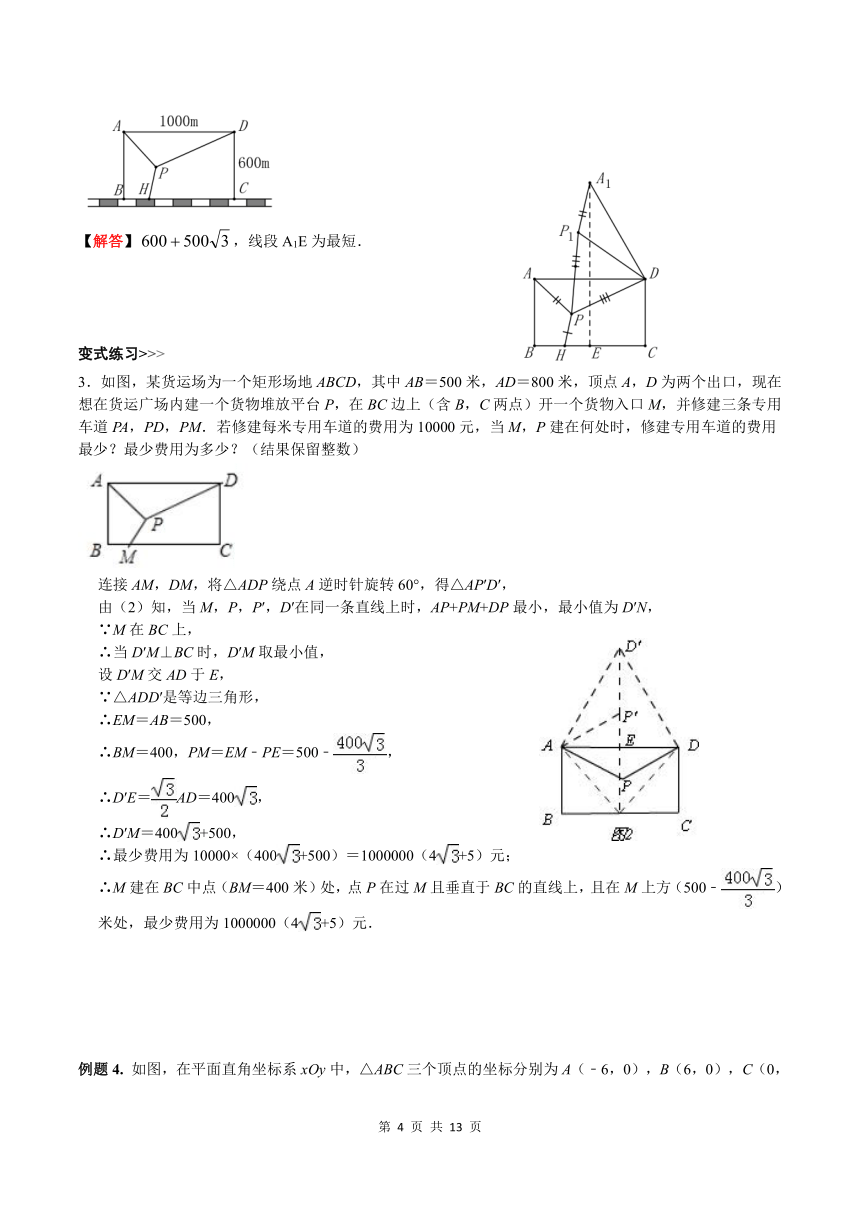
例题1.
已知:△ABC是锐角三角形,G是三角形内一点。∠AGC=∠AGB=∠BGC=120°.
求证:GA+GB+GC的值最小.
证明:将△BGC逆时针旋转60°,连GP,DB.则
△CGB≌△CPD;
∴
∠CPD=∠CGB=120°,CG=CP,GB=PD,
BC=DC,∠GCB=∠PCD.
∵
∠GCP=60°,
∴
∠BCD=60°,
∴
△GCP和△BCD都是等边三角形。
∵
∠AGC=120°,
∠CGP=60°.
∴
A、G、P三点一线。
∵
∠CPD=120°,
∠CPG=60°.
∴
G、P、D三点一线。
∴
AG、GP、PD三条线段同在一条直线上。
∵
GA+GC+GB=GA+GP+PD=AD.
∴
G点是等腰三角形内到三个顶点的距离之和最小的那一点
变式练习>>>
1.如图,是边长为1的等边内的任意一点,求的取值范围.
解:将绕点顺时针旋转60°得到,
易知为等边三角形.
从而
(两点之间线段最短),从而.
过作的平行线分别交于点,
易知.
因为在和中,
①,
②。
又,所以③.
①+②+③可得
,
即.综上,的取值范围为.
例题2.
已知正方形ABCD内一动点E到A、B、C三点的距离之和的最小值为,求正方形的边长.
解
如图2,连接AC,把△AEC绕点C顺时针旋转60°,得到△GFC,连接EF、BG、AG,
可知△EFC、△AGC都是等边三角形,则EF=CE.又FG=AE,
∴AE+BE+CE
=
BE+EF+FG.
∵
点B、点G为定点(G为点A绕C点顺时针旋转60°所得).
∴
线段BG即为点E到A、B、C三点的距离之和的最小值,此时E、F两点都在BG上.
设正方形的边长为,那么
BO=CO=,GC=,
GO=.
∴
BG=BO+GO
=+.
∵
点E到A、B、C三点的距离之和的最小值为.
∴
+=,解得=2.
注
本题旋转△AEB、△BEC也都可以,但都必须绕着定点旋转,读者不妨一试.
变式练习>>>
2.若P为锐角△ABC的费马点,且∠ABC=60°,PA=3,PC=4,
求PB的值.
例题3.
如图,矩形ABCD是一个长为1000米,宽为600米的货场,A、D是入口,现拟在货场内建一个收费站P,在铁路线BC段上建一个发货站台H,设铺设公路AP、DP以及PH之长度和为l,求l的最小值.
【解答】,线段A1E为最短.
变式练习>>>
3.如图,某货运场为一个矩形场地ABCD,其中AB=500米,AD=800米,顶点A,D为两个出口,现在想在货运广场内建一个货物堆放平台P,在BC边上(含B,C两点)开一个货物入口M,并修建三条专用车道PA,PD,PM.若修建每米专用车道的费用为10000元,当M,P建在何处时,修建专用车道的费用最少?最少费用为多少?(结果保留整数)
连接AM,DM,将△ADP绕点A逆时针旋转60°,得△AP′D′,
由(2)知,当M,P,P′,D′在同一条直线上时,AP+PM+DP最小,最小值为D′N,
∵M在BC上,
∴当D′M⊥BC时,D′M取最小值,
设D′M交AD于E,
∵△ADD′是等边三角形,
∴EM=AB=500,
∴BM=400,PM=EM﹣PE=500﹣,
∴D′E=AD=400,
∴D′M=400+500,
∴最少费用为10000×(400+500)=1000000(4+5)元;
∴M建在BC中点(BM=400米)处,点P在过M且垂直于BC的直线上,且在M上方(500﹣)米处,最少费用为1000000(4+5)元.
例题4.
如图,在平面直角坐标系xOy中,△ABC三个顶点的坐标分别为A(﹣6,0),B(6,0),C(0,4),延长AC到点D,使CD=AC,过点D作DE∥AB交BC的延长线于点E.
(1)求D点的坐标;
(2)作C点关于直线DE的对称点F,分别连接DF、EF,若过B点的直线y=kx+b将四边形CDFE分成周长相等的两个四边形,确定此直线的解析式;
(3)在第二问的条件下,设G为y轴上一点,点P从直线y=kx+b与y轴的交点出发,先沿y轴到达G点,再沿GA到达A点,若P点在y轴上运动的速度是它在直线GA上运动速度的2倍,试确定G点的位置,使P点按照上述要求到达A点所用的时间最短.(要求:简述确定G点位置的方法,但不要求证明)
【解答】解:(1)∵A(﹣6,0),C(0,4)
∴OA=6,OC=4,设DE与y轴交于点M
由DE∥AB可得△DMC∽△AOC,又∵CD=AC
∴,∴CM=2,MD=3,同理可得EM=3
∴OM=6,∴D点的坐标为(3,6);
(2)由(1)可得点M的坐标为(0,6)
由DE∥AB,EM=MD,可得y轴所在直线是线段ED的垂直平分线
∴点C关于直线DE的对称点F在y轴上,∴ED与CF互相垂直平分
∴CD=DF=FE=EC,∴四边形CDFE为菱形,且点M为其对称中心
作直线BM,设BM与CD、EF分别交于点S、点T,
可证△FTM≌△CSM,∴FT=CS,
∵FE=CD,∴TE=SD,
∵EC=DF,∴TE+EC+CS+ST=SD+DF+FT+TS,
∴直线BM将四边形CDFE分成周长相等的两个四边形,
由点B(6,0),点M(0,6)在直线y=kx+b上,可得直线BM的解析式为y=﹣x+6.
(3)解法1
∵
BQ=AQ,
∴MQ+2AQ最小就是MQ+AQ+BQ最小,就是在直线MO上找点G使他到A、B、M三点的距离和最小.至此,再次发现这又是一个费尔马问题的变形,注意到题目中等边三角形的信息,考虑作旋转变换.
把△MQB绕点B顺时针旋转60°,得到△M′Q′B,连接QQ′、MM′(图5),可知△QQ′B、△MM′B都是等边三角形,则QQ′=BQ.
又M′Q′=MQ,∴MQ+AQ+BQ=
M′Q′+
QQ′+AQ.
∵点A、M′为定点,所以当Q、Q′两点在线段A
M′上时,MQ+AQ+BQ最小.由条件可证明Q′点总在AM′上,所以A
M′与OM的交点就是所要的G点(图6).可证OG=MG.
图5
图6
图7
解法2
考虑MQ+AQ最小,过Q作BM的垂线交BM于K,由OB=6,OM=,可得∠BMO=30°,所以QK=MQ.要使MQ+AQ最小,只需使AQ+QK最小,?根据“垂线段最短”,可推出当点A、Q、K在一条直线上时,AQ+QK最小,并且此时的QK垂直于BM,此时的点Q即为所求的点G(图7).
过A点作AH⊥BM于H,则AH与y轴的交点为所求的G点.
由OB=6,OM=,可得∠OBM=60°,∴∠BAH=30°
在Rt△OAG中,OG=AO·tan∠BAH=
∴G点的坐标为(0,)(G点为线段OC的中点).
例题5.
如图1,已知一次函数y=x+3的图象与x轴、y轴分别交于A、B两点,抛物线y=﹣x2+bx+c过A、
B两点,且与x轴交于另一点C.
(1)求b、c的值;
(2)如图1,点D为AC的中点,点E在线段BD上,且BE=2ED,连接CE并延长交抛物线于点M,求点M的坐标;
(3)将直线AB绕点A按逆时针方向旋转15°后交y轴于点G,连接CG,如图2,P为△ACG内一点,连接PA、PC、PG,分别以AP、AG为边,在他们的左侧作等边△APR,等边△AGQ,连接QR
①求证:PG=RQ;
②求PA+PC+PG的最小值,并求出当PA+PC+PG取得最小值时点P的坐标.
【解答】解:(1)∵一次函数y=x+3的图象与x轴、y轴分别交于A、B两点,
∴A(﹣3,0),B(0,3),
∵抛物线y=﹣x2+bx+c过A、B两点,∴解得,∴b=﹣2,c=3.
(2),对于抛物线y=﹣x2﹣2x+3,令y=0,则﹣x2﹣2x+3=0,解得x=﹣3或1,
∴点C坐标(1,0),
∵AD=DC=2,∴点D坐标(﹣1,0),
∵BE=2ED,∴点E坐标(﹣,1),
设直线CE为y=kx+b,把E、C代入得到解得,∴直线CE为y=﹣x+,
由解得或,∴点M坐标(﹣,).
(3)①∵△AGQ,△APR是等边三角形,
∴AP=AR,AQ=AG,∠QAC=∠RAP=60°,
∴∠QAR=∠GAP,
在△QAR和△GAP中,,
∴△QAR≌△GAP,∴QR=PG.
②如图3中,∵PA+PG+PC=QR+PR+PC=QC,
∴当Q、R、P、C共线时,PA+PG+PC最小,
作QN⊥OA于N,AM⊥QC于M,PK⊥OA于K.
∵∠GAO=60°,AO=3,
∴AG=QG=AQ=6,∠AGO=30°,
∵∠QGA=60°,∴∠QGO=90°,∴点Q坐标(﹣6,3),
在RT△QCN中,QN=3,CN=7,∠QNC=90°,
∴QC==2,
∵sin∠ACM==,∴AM=,
∵△APR是等边三角形,∴∠APM=60°,∵PM=PR,cos30°=,
∴AP=,PM=RM=,∴MC==,∴PC=CM﹣PM=,
∵==,∴CK=,PK=,∴OK=CK﹣CO=,
∴点P坐标(﹣,).
∴PA+PC+PG的最小值为2,此时点P的坐标(﹣,).
达标检测
领悟提升
强化落实
1.
如图,已知矩形ABCD,AB=4,BC=6,点M为矩形内一点,点E为BC边上任意一点,则MA+MD+ME的最小值为______.
【分析】依然构造60°旋转,将三条折线段转化为一条直线段.
分别以AD、AM为边构造等边△ADF、等边△AMG,连接FG,
易证△AMD≌△AGF,∴MD=GF
∴ME+MA+MD=ME+EG+GF
过F作FH⊥BC交BC于H点,线段FH的长即为所求的最小值.
2.
如图,P为正方形ABCD对角线BD上一动点,若AB=2,则AP+BP+CP的最小值为( )
A.+
B.+
C.4
D.3
【解答】解:如图将△ABP绕点A顺时针旋转60°得到△AEF,
当E、F、P、C共线时,PA+PB+PC最小.
理由:∵AP=AF,∠PAF=60°,
∴△PAF是等边三角形,
∴PA=PF=AF,EF=PB,
∴PA+PB+PC=EF+PF+PC,
∴当E、F、P、C共线时,PA+PB+PC最小,
作EM⊥DA交DA的延长线于M,ME的延长线交CB的延长线于N,则四边形ABNM是矩形,
在RT△AME中,∵∠M=90°,∠MAE=30°,AE=2,
∴ME=1,AM=BN=,MN=AB=2,EN=1,
∴EC===
==
=+.
∴PA+PB+PC的最小值为+.
故选:B.
3.如图,四边形ABCD是菱形,AB=4,且∠ABC=∠ABE=60°,M为对角线BD(不含B点)上任意一点,将BM绕点B逆时针旋转60°得到BN,连接EN、AM、CM,则AM+BM+CM的最小值为 4 .
【解答】解:如图,连接MN,∵△ABE是等边三角形,
∴BA=BE,∠ABE=60°.
∵∠MBN=60°,
∴∠MBN﹣∠ABN=∠ABE﹣∠ABN.
即∠MBA=∠NBE.
又∵MB=NB,
∴△AMB≌△ENB(SAS),
∴AM=EN,
∵∠MBN=60°,MB=NB,
∴△BMN是等边三角形.
∴BM=MN.
∴AM+BM+CM=EN+MN+CM.
根据“两点之间线段最短”,得EN+MN+CM=EC最短
∴当M点位于BD与CE的交点处时,AM+BM+CM的值最小,即等于EC的长,
过E点作EF⊥BC交CB的延长线于F,
∴∠EBF=180°﹣120°=60°,
∵BC=4,
∴BF=2,EF=2,在Rt△EFC中,
∵EF2+FC2=EC2,
EC=4.
故答案为:4
4.将△ABC放在每个小正方形的边长为1的网格中,点B、C落在格点上,点A在BC的垂直平分线上,∠ABC=30°,点P为平面内一点.
(1)∠ACB= 30 度;
(2)如图,将△APC绕点C顺时针旋转60°,画出旋转后的图形(尺规作图,保留痕迹);
(3)AP+BP+CP的最小值为 .
【解答】解(1)∵点A在BC的垂直平分线上.
∴AB=AC,
∴∠ABC=∠ACB,
∵∠ABC=30°,
∴∠ACB=30°.
故答案为30°.
(2)如图△CA′P′就是所求的三角形.
(3)如图当B、P、P′、A′共线时,PA+PB+PC=PB+PP′+P′A的值最小,
此时BC=5,AC=CA′=,BA′==.
故答案为.
5.如图,四个村庄坐落在矩形ABCD的四个顶点上,AB=10公里,BC=15公里,现在要设立两个车站E,F,则EA+EB+EF+FC+FD的最小值为 (15+10) 公里.
【解答】解:如图1,将△AEB绕A顺时针旋转60°得△AGH,连接BH、EG,将△DFC绕点D逆时针旋转60°得到△DF'M,连接CM、FF',
由旋转得:AB=AH,AE=AG,∠EAG=∠BAH=60°,BE=GH,
∴△AEG和△ABH是等边三角形,
∴AE=EG,
同理得:△DFF'和△DCM是等边三角形,DF=FF',FC=F'M,
∴当H、G、E、F、F'、M在同一条直线上时,EA+EB+EF+FC+FD有最小值,如图2,
∵AH=BH,DM=CM,
∴HM是AB和CD的垂直平分线,
∴HM⊥AB,HM⊥CD,
∵AB=10,
∴△ABH的高为5,
∴EA+EB+EF+FC+FD=EG+GH+EF+FF'+F'M=HM=15+5+5=15+10,
则EA+EB+EF+FC+FD的最小值是(15+10)公理.
故答案为:(15+10).
6.已知,在△ABC中,∠ACB=30°
(1)如图1,当AB=AC=2,求BC的值;
(2)如图2,当AB=AC,点P是△ABC内一点,且PA=2,PB=,PC=3,求∠APC的度数;
(3)如图3,当AC=4,AB=(CB>CA),点P是△ABC内一动点,则PA+PB+PC的最小值为 .
【解答】解:(1)如图1中,作AP⊥BC于P.
∵AB=AC,AP⊥BC,
∴BP=PC,
在Rt△ACP中,∵AC=2,∠C=30°,
∴PC=AC?cos30°=,
∴BC=2PC=2.
(2)如图2中,将△APB绕点A逆时针旋转120°得到△QAC.
∵AB=AC,∠C=30°,
∴∠BAC=120°,
∴PA=AQ=2,PB=QC=,
∵∠PAQ=120°,
∴PQ=2,
∴PQ2+PC2=QC2,
∴∠QPC=90°,
∵∠APQ=30°,
∴∠APC=30°+90°=120°.
(3)如图3中,将△BCP绕点C逆时针旋转60°得到△CB′P′,连接PP′,AB′,则∠ACB′=90°.
∵PA+PB+PC=PA+PP′+P′B′,
∴当A,P,P′,B′共线时,PA+PB+PC的值最小,最小值=AB′的长,
由AB=,AC=4,∠C=30°,可得BC=CB′=3,
∴AB′==.
故答案为.
7.如图l,在△ABC中,∠ACB=90°,点P为△ABC内一点.
(1)连接PB,PC,将△BCP沿射线CA方向平移,得到△DAE,点B,C,P的对应点分别为点D、A、E,连接CE.
①依题意,请在图2中补全图形;
②如果BP⊥CE,BP=3,AB=6,求CE的长
(2)如图3,以点A为旋转中心,将△ABP顺时针旋转60°得到△AMN,连接PA、PB、PC,当AC=3,AB=6时,根据此图求PA+PB+PC的最小值.
【解答】解:(1)①补全图形如图所示;
②如图,连接BD、CD
∵△BCP沿射线CA方向平移,得到△DAE,
∴BC∥AD且BC=AD,
∵∠ACB=90°,
∴四边形BCAD是矩形,
∴CD=AB=6,
∵BP=3,
∴DE=BP=3,
∵BP⊥CE,BP∥DE,
∴DE⊥CE,
∴在Rt△DCE中,CE===3;
(2)证明:如图所示,以点A为旋转中心,将△ABP顺时针旋转60°得到△AMN,连接BN.
由旋转可得,△AMN≌△ABP,
∴MN=BP,PA=AM,∠PAM=60°=∠BAN,AB=AN,
∴△PAM、△ABN都是等边三角形,
∴PA=PM,
∴PA+PB+PC=CP+PM+MN,
当AC=3,AB=6时,BC=3,
∴sin∠ABC=,
∴∠ABC=30°,∵∠ABN=60°,
∴∠CBN=90°
当C、P、M、N四点共线时,PA+PB+PC的值最小,
最小值=CN===3.
8.(1)阅读证明
①如图1,在△ABC所在平面上存在一点P,使它到三角形三顶点的距离之和最小,则称点P为△ABC的费马点,此时PA+PB+PC的值为△ABC的费马距离.
②如图2,已知点P为等边△ABC外接圆的上任意一点.求证:PB+PC=PA.
(2)知识迁移
根据(1)的结论,我们有如下探寻△ABC(其中∠A,∠B,∠C均小于120°)的费马点和费马距离的方法:
第一步:如图3,在△ABC的外部以BC为边长作等边△BCD及其外接圆;
第二步:在上取一点P0,连接P0A,P0B,P0C,P0D.易知P0A+P0B+P0C=P0A+(P0B+P0C)=P0A+ P0D ;
第三步:根据(1)①中定义,在图3中找出△ABC的费马点P,线段 AD 的长度即为△ABC的费马距离.
(3)知识应用
已知三村庄A,B,C构成了如图4所示的△ABC(其中∠A,∠B,∠C均小于120°),现选取一点P打水井,使水井P到三村庄A,B,C所铺设的输水管总长度最小.求输水管总长度的最小值.
【解答】解:(1)如图2,延长BP至E,使PE=PC.
∵在等边△ABC中,∴∠EPC=∠BAC=60°,
∵PC=PE,∴△PCE为等边三角形,
∴PC=PE,∠PCE=60°,
∴∠BCP+∠PCE=∠ACB+∠BCP,
∴∠ACP=∠BCE,
∵在△ACP和△BCE中,
,
∴△ACP≌△BCE(SAS).
∴AP=BE=BP+PE=BP+PC;
(2)由(1)得出:第一步:如图3,在△ABC的外部以BC为边长作等边△BCD及其外接圆;
第二步:在上取一点P0,连接P0A,P0B,P0C,P0D.易知P0A+P0B+P0C=P0A+(P0B+P0C)=P0A+P0D;
第三步:根据(1)①中定义,在图3中找出△ABC的费马点P,线段AD的长度即为△ABC的费马距离.
故答案为:P0D;AD.
(3)如图4,以BC为边在△ABC的外部作等边△BCD,连接AD.
∴AD的长就是△ABC的费马距离.
可得∠ABD=90°
∴AD==5(km).
∴输水管总长度的最小值为5千米.
费马尔问题思考:
如何找一点P使它到△ABC三个顶点的距离之和PA+PB+PC最小?
当B、P、Q、E四点共线时取得最小值
费马点的定义:数学上称,到三角形3个顶点距离之和最小的点为费马点。
它是这样确定的:
1.
如果三角形有一个内角大于或等于120°,这个内角的顶点就是费马点;
2.
如果3个内角均小于120°,则在三角形内部对3边张角均为120°的点,是三角形的费马点。
费马点的性质:费马点有如下主要性质:
1.费马点到三角形三个顶点距离之和最小。
2.费马点连接三顶点所成的三夹角皆为120°。
费马点最小值快速求解:
费尔马问题告诉我们,存在这么一个点到三个定点的距离的和最小,解决问题的方法是运用旋转变换.
秘诀:以△ABC任意一边为边向外作等边三角形,这条边所对两顶点的距离即为最小值
典题探究
例题1.
已知:△ABC是锐角三角形,G是三角形内一点。∠AGC=∠AGB=∠BGC=120°.
求证:GA+GB+GC的值最小.
证明:将△BGC逆时针旋转60°,连GP,DB.则
△CGB≌△CPD;
∴
∠CPD=∠CGB=120°,CG=CP,GB=PD,
BC=DC,∠GCB=∠PCD.
∵
∠GCP=60°,
∴
∠BCD=60°,
∴
△GCP和△BCD都是等边三角形。
∵
∠AGC=120°,
∠CGP=60°.
∴
A、G、P三点一线。
∵
∠CPD=120°,
∠CPG=60°.
∴
G、P、D三点一线。
∴
AG、GP、PD三条线段同在一条直线上。
∵
GA+GC+GB=GA+GP+PD=AD.
∴
G点是等腰三角形内到三个顶点的距离之和最小的那一点
变式练习>>>
1.如图,是边长为1的等边内的任意一点,求的取值范围.
解:将绕点顺时针旋转60°得到,
易知为等边三角形.
从而
(两点之间线段最短),从而.
过作的平行线分别交于点,
易知.
因为在和中,
①,
②。
又,所以③.
①+②+③可得
,
即.综上,的取值范围为.
例题2.
已知正方形ABCD内一动点E到A、B、C三点的距离之和的最小值为,求正方形的边长.
解
如图2,连接AC,把△AEC绕点C顺时针旋转60°,得到△GFC,连接EF、BG、AG,
可知△EFC、△AGC都是等边三角形,则EF=CE.又FG=AE,
∴AE+BE+CE
=
BE+EF+FG.
∵
点B、点G为定点(G为点A绕C点顺时针旋转60°所得).
∴
线段BG即为点E到A、B、C三点的距离之和的最小值,此时E、F两点都在BG上.
设正方形的边长为,那么
BO=CO=,GC=,
GO=.
∴
BG=BO+GO
=+.
∵
点E到A、B、C三点的距离之和的最小值为.
∴
+=,解得=2.
注
本题旋转△AEB、△BEC也都可以,但都必须绕着定点旋转,读者不妨一试.
变式练习>>>
2.若P为锐角△ABC的费马点,且∠ABC=60°,PA=3,PC=4,
求PB的值.
例题3.
如图,矩形ABCD是一个长为1000米,宽为600米的货场,A、D是入口,现拟在货场内建一个收费站P,在铁路线BC段上建一个发货站台H,设铺设公路AP、DP以及PH之长度和为l,求l的最小值.
【解答】,线段A1E为最短.
变式练习>>>
3.如图,某货运场为一个矩形场地ABCD,其中AB=500米,AD=800米,顶点A,D为两个出口,现在想在货运广场内建一个货物堆放平台P,在BC边上(含B,C两点)开一个货物入口M,并修建三条专用车道PA,PD,PM.若修建每米专用车道的费用为10000元,当M,P建在何处时,修建专用车道的费用最少?最少费用为多少?(结果保留整数)
连接AM,DM,将△ADP绕点A逆时针旋转60°,得△AP′D′,
由(2)知,当M,P,P′,D′在同一条直线上时,AP+PM+DP最小,最小值为D′N,
∵M在BC上,
∴当D′M⊥BC时,D′M取最小值,
设D′M交AD于E,
∵△ADD′是等边三角形,
∴EM=AB=500,
∴BM=400,PM=EM﹣PE=500﹣,
∴D′E=AD=400,
∴D′M=400+500,
∴最少费用为10000×(400+500)=1000000(4+5)元;
∴M建在BC中点(BM=400米)处,点P在过M且垂直于BC的直线上,且在M上方(500﹣)米处,最少费用为1000000(4+5)元.
例题4.
如图,在平面直角坐标系xOy中,△ABC三个顶点的坐标分别为A(﹣6,0),B(6,0),C(0,4),延长AC到点D,使CD=AC,过点D作DE∥AB交BC的延长线于点E.
(1)求D点的坐标;
(2)作C点关于直线DE的对称点F,分别连接DF、EF,若过B点的直线y=kx+b将四边形CDFE分成周长相等的两个四边形,确定此直线的解析式;
(3)在第二问的条件下,设G为y轴上一点,点P从直线y=kx+b与y轴的交点出发,先沿y轴到达G点,再沿GA到达A点,若P点在y轴上运动的速度是它在直线GA上运动速度的2倍,试确定G点的位置,使P点按照上述要求到达A点所用的时间最短.(要求:简述确定G点位置的方法,但不要求证明)
【解答】解:(1)∵A(﹣6,0),C(0,4)
∴OA=6,OC=4,设DE与y轴交于点M
由DE∥AB可得△DMC∽△AOC,又∵CD=AC
∴,∴CM=2,MD=3,同理可得EM=3
∴OM=6,∴D点的坐标为(3,6);
(2)由(1)可得点M的坐标为(0,6)
由DE∥AB,EM=MD,可得y轴所在直线是线段ED的垂直平分线
∴点C关于直线DE的对称点F在y轴上,∴ED与CF互相垂直平分
∴CD=DF=FE=EC,∴四边形CDFE为菱形,且点M为其对称中心
作直线BM,设BM与CD、EF分别交于点S、点T,
可证△FTM≌△CSM,∴FT=CS,
∵FE=CD,∴TE=SD,
∵EC=DF,∴TE+EC+CS+ST=SD+DF+FT+TS,
∴直线BM将四边形CDFE分成周长相等的两个四边形,
由点B(6,0),点M(0,6)在直线y=kx+b上,可得直线BM的解析式为y=﹣x+6.
(3)解法1
∵
BQ=AQ,
∴MQ+2AQ最小就是MQ+AQ+BQ最小,就是在直线MO上找点G使他到A、B、M三点的距离和最小.至此,再次发现这又是一个费尔马问题的变形,注意到题目中等边三角形的信息,考虑作旋转变换.
把△MQB绕点B顺时针旋转60°,得到△M′Q′B,连接QQ′、MM′(图5),可知△QQ′B、△MM′B都是等边三角形,则QQ′=BQ.
又M′Q′=MQ,∴MQ+AQ+BQ=
M′Q′+
QQ′+AQ.
∵点A、M′为定点,所以当Q、Q′两点在线段A
M′上时,MQ+AQ+BQ最小.由条件可证明Q′点总在AM′上,所以A
M′与OM的交点就是所要的G点(图6).可证OG=MG.
图5
图6
图7
解法2
考虑MQ+AQ最小,过Q作BM的垂线交BM于K,由OB=6,OM=,可得∠BMO=30°,所以QK=MQ.要使MQ+AQ最小,只需使AQ+QK最小,?根据“垂线段最短”,可推出当点A、Q、K在一条直线上时,AQ+QK最小,并且此时的QK垂直于BM,此时的点Q即为所求的点G(图7).
过A点作AH⊥BM于H,则AH与y轴的交点为所求的G点.
由OB=6,OM=,可得∠OBM=60°,∴∠BAH=30°
在Rt△OAG中,OG=AO·tan∠BAH=
∴G点的坐标为(0,)(G点为线段OC的中点).
例题5.
如图1,已知一次函数y=x+3的图象与x轴、y轴分别交于A、B两点,抛物线y=﹣x2+bx+c过A、
B两点,且与x轴交于另一点C.
(1)求b、c的值;
(2)如图1,点D为AC的中点,点E在线段BD上,且BE=2ED,连接CE并延长交抛物线于点M,求点M的坐标;
(3)将直线AB绕点A按逆时针方向旋转15°后交y轴于点G,连接CG,如图2,P为△ACG内一点,连接PA、PC、PG,分别以AP、AG为边,在他们的左侧作等边△APR,等边△AGQ,连接QR
①求证:PG=RQ;
②求PA+PC+PG的最小值,并求出当PA+PC+PG取得最小值时点P的坐标.
【解答】解:(1)∵一次函数y=x+3的图象与x轴、y轴分别交于A、B两点,
∴A(﹣3,0),B(0,3),
∵抛物线y=﹣x2+bx+c过A、B两点,∴解得,∴b=﹣2,c=3.
(2),对于抛物线y=﹣x2﹣2x+3,令y=0,则﹣x2﹣2x+3=0,解得x=﹣3或1,
∴点C坐标(1,0),
∵AD=DC=2,∴点D坐标(﹣1,0),
∵BE=2ED,∴点E坐标(﹣,1),
设直线CE为y=kx+b,把E、C代入得到解得,∴直线CE为y=﹣x+,
由解得或,∴点M坐标(﹣,).
(3)①∵△AGQ,△APR是等边三角形,
∴AP=AR,AQ=AG,∠QAC=∠RAP=60°,
∴∠QAR=∠GAP,
在△QAR和△GAP中,,
∴△QAR≌△GAP,∴QR=PG.
②如图3中,∵PA+PG+PC=QR+PR+PC=QC,
∴当Q、R、P、C共线时,PA+PG+PC最小,
作QN⊥OA于N,AM⊥QC于M,PK⊥OA于K.
∵∠GAO=60°,AO=3,
∴AG=QG=AQ=6,∠AGO=30°,
∵∠QGA=60°,∴∠QGO=90°,∴点Q坐标(﹣6,3),
在RT△QCN中,QN=3,CN=7,∠QNC=90°,
∴QC==2,
∵sin∠ACM==,∴AM=,
∵△APR是等边三角形,∴∠APM=60°,∵PM=PR,cos30°=,
∴AP=,PM=RM=,∴MC==,∴PC=CM﹣PM=,
∵==,∴CK=,PK=,∴OK=CK﹣CO=,
∴点P坐标(﹣,).
∴PA+PC+PG的最小值为2,此时点P的坐标(﹣,).
达标检测
领悟提升
强化落实
1.
如图,已知矩形ABCD,AB=4,BC=6,点M为矩形内一点,点E为BC边上任意一点,则MA+MD+ME的最小值为______.
【分析】依然构造60°旋转,将三条折线段转化为一条直线段.
分别以AD、AM为边构造等边△ADF、等边△AMG,连接FG,
易证△AMD≌△AGF,∴MD=GF
∴ME+MA+MD=ME+EG+GF
过F作FH⊥BC交BC于H点,线段FH的长即为所求的最小值.
2.
如图,P为正方形ABCD对角线BD上一动点,若AB=2,则AP+BP+CP的最小值为( )
A.+
B.+
C.4
D.3
【解答】解:如图将△ABP绕点A顺时针旋转60°得到△AEF,
当E、F、P、C共线时,PA+PB+PC最小.
理由:∵AP=AF,∠PAF=60°,
∴△PAF是等边三角形,
∴PA=PF=AF,EF=PB,
∴PA+PB+PC=EF+PF+PC,
∴当E、F、P、C共线时,PA+PB+PC最小,
作EM⊥DA交DA的延长线于M,ME的延长线交CB的延长线于N,则四边形ABNM是矩形,
在RT△AME中,∵∠M=90°,∠MAE=30°,AE=2,
∴ME=1,AM=BN=,MN=AB=2,EN=1,
∴EC===
==
=+.
∴PA+PB+PC的最小值为+.
故选:B.
3.如图,四边形ABCD是菱形,AB=4,且∠ABC=∠ABE=60°,M为对角线BD(不含B点)上任意一点,将BM绕点B逆时针旋转60°得到BN,连接EN、AM、CM,则AM+BM+CM的最小值为 4 .
【解答】解:如图,连接MN,∵△ABE是等边三角形,
∴BA=BE,∠ABE=60°.
∵∠MBN=60°,
∴∠MBN﹣∠ABN=∠ABE﹣∠ABN.
即∠MBA=∠NBE.
又∵MB=NB,
∴△AMB≌△ENB(SAS),
∴AM=EN,
∵∠MBN=60°,MB=NB,
∴△BMN是等边三角形.
∴BM=MN.
∴AM+BM+CM=EN+MN+CM.
根据“两点之间线段最短”,得EN+MN+CM=EC最短
∴当M点位于BD与CE的交点处时,AM+BM+CM的值最小,即等于EC的长,
过E点作EF⊥BC交CB的延长线于F,
∴∠EBF=180°﹣120°=60°,
∵BC=4,
∴BF=2,EF=2,在Rt△EFC中,
∵EF2+FC2=EC2,
EC=4.
故答案为:4
4.将△ABC放在每个小正方形的边长为1的网格中,点B、C落在格点上,点A在BC的垂直平分线上,∠ABC=30°,点P为平面内一点.
(1)∠ACB= 30 度;
(2)如图,将△APC绕点C顺时针旋转60°,画出旋转后的图形(尺规作图,保留痕迹);
(3)AP+BP+CP的最小值为 .
【解答】解(1)∵点A在BC的垂直平分线上.
∴AB=AC,
∴∠ABC=∠ACB,
∵∠ABC=30°,
∴∠ACB=30°.
故答案为30°.
(2)如图△CA′P′就是所求的三角形.
(3)如图当B、P、P′、A′共线时,PA+PB+PC=PB+PP′+P′A的值最小,
此时BC=5,AC=CA′=,BA′==.
故答案为.
5.如图,四个村庄坐落在矩形ABCD的四个顶点上,AB=10公里,BC=15公里,现在要设立两个车站E,F,则EA+EB+EF+FC+FD的最小值为 (15+10) 公里.
【解答】解:如图1,将△AEB绕A顺时针旋转60°得△AGH,连接BH、EG,将△DFC绕点D逆时针旋转60°得到△DF'M,连接CM、FF',
由旋转得:AB=AH,AE=AG,∠EAG=∠BAH=60°,BE=GH,
∴△AEG和△ABH是等边三角形,
∴AE=EG,
同理得:△DFF'和△DCM是等边三角形,DF=FF',FC=F'M,
∴当H、G、E、F、F'、M在同一条直线上时,EA+EB+EF+FC+FD有最小值,如图2,
∵AH=BH,DM=CM,
∴HM是AB和CD的垂直平分线,
∴HM⊥AB,HM⊥CD,
∵AB=10,
∴△ABH的高为5,
∴EA+EB+EF+FC+FD=EG+GH+EF+FF'+F'M=HM=15+5+5=15+10,
则EA+EB+EF+FC+FD的最小值是(15+10)公理.
故答案为:(15+10).
6.已知,在△ABC中,∠ACB=30°
(1)如图1,当AB=AC=2,求BC的值;
(2)如图2,当AB=AC,点P是△ABC内一点,且PA=2,PB=,PC=3,求∠APC的度数;
(3)如图3,当AC=4,AB=(CB>CA),点P是△ABC内一动点,则PA+PB+PC的最小值为 .
【解答】解:(1)如图1中,作AP⊥BC于P.
∵AB=AC,AP⊥BC,
∴BP=PC,
在Rt△ACP中,∵AC=2,∠C=30°,
∴PC=AC?cos30°=,
∴BC=2PC=2.
(2)如图2中,将△APB绕点A逆时针旋转120°得到△QAC.
∵AB=AC,∠C=30°,
∴∠BAC=120°,
∴PA=AQ=2,PB=QC=,
∵∠PAQ=120°,
∴PQ=2,
∴PQ2+PC2=QC2,
∴∠QPC=90°,
∵∠APQ=30°,
∴∠APC=30°+90°=120°.
(3)如图3中,将△BCP绕点C逆时针旋转60°得到△CB′P′,连接PP′,AB′,则∠ACB′=90°.
∵PA+PB+PC=PA+PP′+P′B′,
∴当A,P,P′,B′共线时,PA+PB+PC的值最小,最小值=AB′的长,
由AB=,AC=4,∠C=30°,可得BC=CB′=3,
∴AB′==.
故答案为.
7.如图l,在△ABC中,∠ACB=90°,点P为△ABC内一点.
(1)连接PB,PC,将△BCP沿射线CA方向平移,得到△DAE,点B,C,P的对应点分别为点D、A、E,连接CE.
①依题意,请在图2中补全图形;
②如果BP⊥CE,BP=3,AB=6,求CE的长
(2)如图3,以点A为旋转中心,将△ABP顺时针旋转60°得到△AMN,连接PA、PB、PC,当AC=3,AB=6时,根据此图求PA+PB+PC的最小值.
【解答】解:(1)①补全图形如图所示;
②如图,连接BD、CD
∵△BCP沿射线CA方向平移,得到△DAE,
∴BC∥AD且BC=AD,
∵∠ACB=90°,
∴四边形BCAD是矩形,
∴CD=AB=6,
∵BP=3,
∴DE=BP=3,
∵BP⊥CE,BP∥DE,
∴DE⊥CE,
∴在Rt△DCE中,CE===3;
(2)证明:如图所示,以点A为旋转中心,将△ABP顺时针旋转60°得到△AMN,连接BN.
由旋转可得,△AMN≌△ABP,
∴MN=BP,PA=AM,∠PAM=60°=∠BAN,AB=AN,
∴△PAM、△ABN都是等边三角形,
∴PA=PM,
∴PA+PB+PC=CP+PM+MN,
当AC=3,AB=6时,BC=3,
∴sin∠ABC=,
∴∠ABC=30°,∵∠ABN=60°,
∴∠CBN=90°
当C、P、M、N四点共线时,PA+PB+PC的值最小,
最小值=CN===3.
8.(1)阅读证明
①如图1,在△ABC所在平面上存在一点P,使它到三角形三顶点的距离之和最小,则称点P为△ABC的费马点,此时PA+PB+PC的值为△ABC的费马距离.
②如图2,已知点P为等边△ABC外接圆的上任意一点.求证:PB+PC=PA.
(2)知识迁移
根据(1)的结论,我们有如下探寻△ABC(其中∠A,∠B,∠C均小于120°)的费马点和费马距离的方法:
第一步:如图3,在△ABC的外部以BC为边长作等边△BCD及其外接圆;
第二步:在上取一点P0,连接P0A,P0B,P0C,P0D.易知P0A+P0B+P0C=P0A+(P0B+P0C)=P0A+ P0D ;
第三步:根据(1)①中定义,在图3中找出△ABC的费马点P,线段 AD 的长度即为△ABC的费马距离.
(3)知识应用
已知三村庄A,B,C构成了如图4所示的△ABC(其中∠A,∠B,∠C均小于120°),现选取一点P打水井,使水井P到三村庄A,B,C所铺设的输水管总长度最小.求输水管总长度的最小值.
【解答】解:(1)如图2,延长BP至E,使PE=PC.
∵在等边△ABC中,∴∠EPC=∠BAC=60°,
∵PC=PE,∴△PCE为等边三角形,
∴PC=PE,∠PCE=60°,
∴∠BCP+∠PCE=∠ACB+∠BCP,
∴∠ACP=∠BCE,
∵在△ACP和△BCE中,
,
∴△ACP≌△BCE(SAS).
∴AP=BE=BP+PE=BP+PC;
(2)由(1)得出:第一步:如图3,在△ABC的外部以BC为边长作等边△BCD及其外接圆;
第二步:在上取一点P0,连接P0A,P0B,P0C,P0D.易知P0A+P0B+P0C=P0A+(P0B+P0C)=P0A+P0D;
第三步:根据(1)①中定义,在图3中找出△ABC的费马点P,线段AD的长度即为△ABC的费马距离.
故答案为:P0D;AD.
(3)如图4,以BC为边在△ABC的外部作等边△BCD,连接AD.
∴AD的长就是△ABC的费马距离.
可得∠ABD=90°
∴AD==5(km).
∴输水管总长度的最小值为5千米.
同课章节目录
