沪科版九年级数学下册24.4.2切线判定定理知识点复习学案(表格式 无答案)
文档属性
| 名称 | 沪科版九年级数学下册24.4.2切线判定定理知识点复习学案(表格式 无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 247.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-21 08:06:59 | ||
图片预览


文档简介
年级
九年级
教学内容
切线判定定理
教学过程
【知识点一、直线和圆的位置关系】
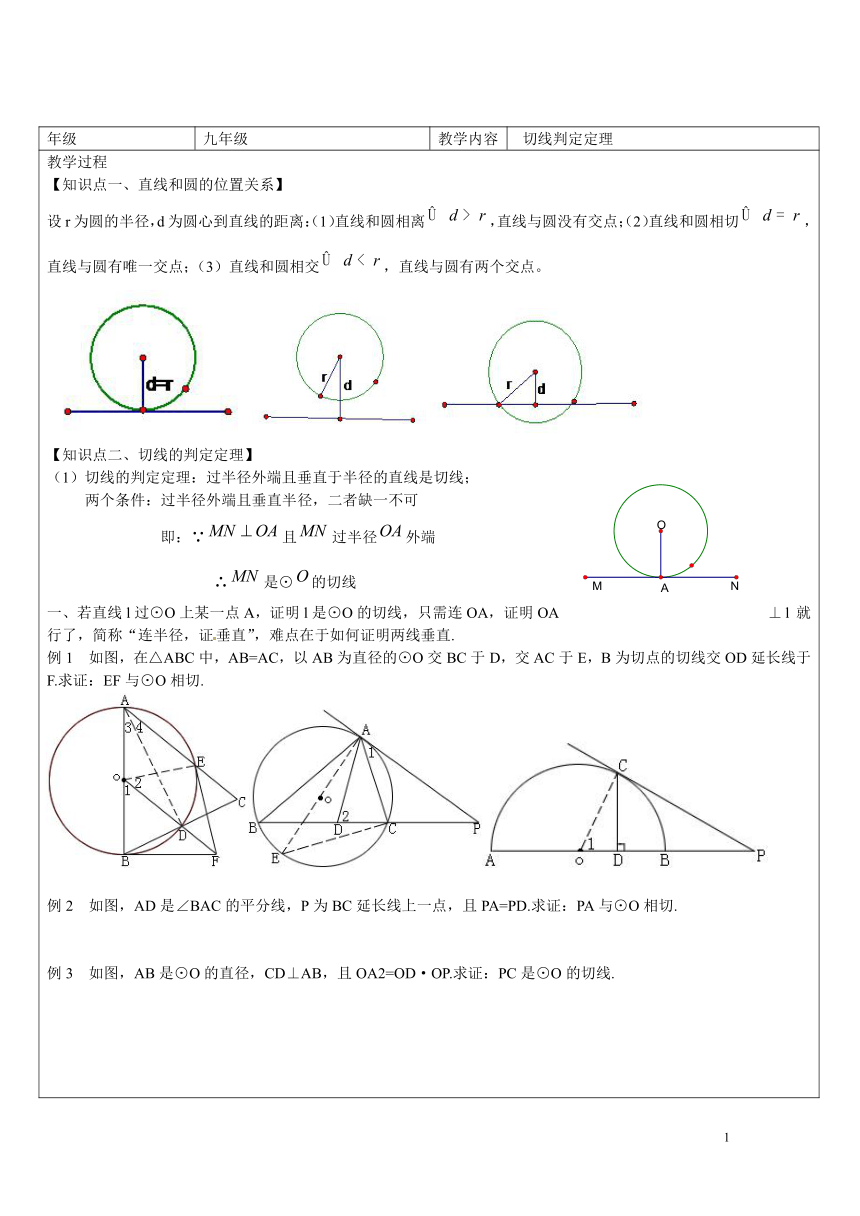
设r为圆的半径,d为圆心到直线的距离:(1)直线和圆相离,直线与圆没有交点;(2)直线和圆相切,直线与圆有唯一交点;(3)直线和圆相交,直线与圆有两个交点。
【知识点二、切线的判定定理】
(1)切线的判定定理:过半径外端且垂直于半径的直线是切线;
两个条件:过半径外端且垂直半径,二者缺一不可
即:∵且过半径外端
∴是⊙的切线
一、若直线l过⊙O上某一点A,证明l是⊙O的切线,只需连OA,证明OA⊥l就行了,简称“连半径,证垂直”,难点在于如何证明两线垂直.
例1
如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于D,交AC于E,B为切点的切线交OD延长线于F.求证:EF与⊙O相切.
例2
如图,AD是∠BAC的平分线,P为BC延长线上一点,且PA=PD.求证:PA与⊙O相切.
例3
如图,AB是⊙O的直径,CD⊥AB,且OA2=OD·OP.求证:PC是⊙O的切线.
二、若直线l与⊙O没有已知的公共点,又要证明l是⊙O的切线,只需作OA⊥l,A为垂足,证明OA是⊙O的半径就行了,简称:“作垂直;证半径”
例4
已知:如图,AC,BD与⊙O切于A、B,且AC∥BD,若∠COD=900.
求证:CD是⊙O的切线.
例5已知:如图,是的直径,是上一点,于点,过点作的切线,交
的延长线于点,连结.
⑴
求证:与相切;
⑵
连结并延长交于点,,求的长.
巩固练习
1、如图,直线AB经过⊙O上的点C,直线AO与⊙O交于点E和点D,OB与OD交于点F,连接DF,DC.已知OA=OB,
CA=CB,DE=10,DF=6.
(1)求证:①直线AB是⊙O的切线;②∠FDC=∠EDC;
(2)求CD的长.
2.如图,已知⊙O的直径AB=10,弦AC=6,∠BAC的平分线交⊙O于点D,过点D作DE⊥AC交AC的延长线于点E.
(1)求证:DE是⊙O的切线.
(2)求DE的长.
3.如图,在⊙O中,弦AB=OA,P是半径OB的延长线上一点,且PB=OB,则PA与⊙O的位置关系是_________.
第3题
第4题
第5题
4.如图,△ABC的一边AB是⊙O的直径,请你添加一个条件,使BC是⊙O的切线,你所添加的条件为________________.
5.如图,AB是⊙O的直径,O是圆心,BC与⊙O切于点B,CO交⊙O于点D,且BC=8,CD=4,那么⊙O的半径是______.
6.
如图,若以平行四边形一边AB为直径的圆恰好与对边CD相切于点D,则∠C=_______度.
第6题
第7题
第8题
7、
如图,AB为⊙O的直径,直线l与⊙O相切于点C,AD⊥l,垂足为D,AD交⊙O于点E,连接OC,BE.若AE=6,OA=5,则线段DC的长为______.
8、如图,已知△ABC内接于⊙O,BC是⊙O的直径,MN与⊙O相切,切点为A,若∠MAB=30°,则∠B=
度.
证明题
1、如图,C是以AB为直径的⊙O上一点,过O作OE⊥AC于点E,过点A作⊙O的切线
交OE的延长线于点F,
连结CF并延长交BA的延长线于点P.
⑴
求证:PC是⊙O的切线.⑵
若AB=4,,求CF的长.
如图,已知中,,平分,以为圆心、长为半径作,与的另一个交点为.
⑴
求证:与相切;⑵
若,求的长.
类型之二 与切线的判定有关的计算或证明
如图,⊙O的直径为AB,点C在圆周上(异于A,B),AD⊥CD.
(1)若BC=3,AB=5,求AC的值;
(2)若AC是∠DAB的平分线,求证:直线CD是⊙O的切线.
如图,在Rt△ACB中,∠ACB=90°,以AC为直径作⊙O交AB于点D,E为BC的中点,连结DE并延长交AC的延长线点F.
(1)求证:DE是⊙O的切线;
(2)若CF=2,DF=4,求⊙O直径的长.
如图,AB是⊙O的直径,点C,D在⊙O上,∠A=2∠BCD,点E在AB的延长线上,∠AED=∠ABC.
(1)求证:DE与⊙O相切;
(2)若BF=2,DF=,求⊙O的半径.
4
九年级
教学内容
切线判定定理
教学过程
【知识点一、直线和圆的位置关系】
设r为圆的半径,d为圆心到直线的距离:(1)直线和圆相离,直线与圆没有交点;(2)直线和圆相切,直线与圆有唯一交点;(3)直线和圆相交,直线与圆有两个交点。
【知识点二、切线的判定定理】
(1)切线的判定定理:过半径外端且垂直于半径的直线是切线;
两个条件:过半径外端且垂直半径,二者缺一不可
即:∵且过半径外端
∴是⊙的切线
一、若直线l过⊙O上某一点A,证明l是⊙O的切线,只需连OA,证明OA⊥l就行了,简称“连半径,证垂直”,难点在于如何证明两线垂直.
例1
如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于D,交AC于E,B为切点的切线交OD延长线于F.求证:EF与⊙O相切.
例2
如图,AD是∠BAC的平分线,P为BC延长线上一点,且PA=PD.求证:PA与⊙O相切.
例3
如图,AB是⊙O的直径,CD⊥AB,且OA2=OD·OP.求证:PC是⊙O的切线.
二、若直线l与⊙O没有已知的公共点,又要证明l是⊙O的切线,只需作OA⊥l,A为垂足,证明OA是⊙O的半径就行了,简称:“作垂直;证半径”
例4
已知:如图,AC,BD与⊙O切于A、B,且AC∥BD,若∠COD=900.
求证:CD是⊙O的切线.
例5已知:如图,是的直径,是上一点,于点,过点作的切线,交
的延长线于点,连结.
⑴
求证:与相切;
⑵
连结并延长交于点,,求的长.
巩固练习
1、如图,直线AB经过⊙O上的点C,直线AO与⊙O交于点E和点D,OB与OD交于点F,连接DF,DC.已知OA=OB,
CA=CB,DE=10,DF=6.
(1)求证:①直线AB是⊙O的切线;②∠FDC=∠EDC;
(2)求CD的长.
2.如图,已知⊙O的直径AB=10,弦AC=6,∠BAC的平分线交⊙O于点D,过点D作DE⊥AC交AC的延长线于点E.
(1)求证:DE是⊙O的切线.
(2)求DE的长.
3.如图,在⊙O中,弦AB=OA,P是半径OB的延长线上一点,且PB=OB,则PA与⊙O的位置关系是_________.
第3题
第4题
第5题
4.如图,△ABC的一边AB是⊙O的直径,请你添加一个条件,使BC是⊙O的切线,你所添加的条件为________________.
5.如图,AB是⊙O的直径,O是圆心,BC与⊙O切于点B,CO交⊙O于点D,且BC=8,CD=4,那么⊙O的半径是______.
6.
如图,若以平行四边形一边AB为直径的圆恰好与对边CD相切于点D,则∠C=_______度.
第6题
第7题
第8题
7、
如图,AB为⊙O的直径,直线l与⊙O相切于点C,AD⊥l,垂足为D,AD交⊙O于点E,连接OC,BE.若AE=6,OA=5,则线段DC的长为______.
8、如图,已知△ABC内接于⊙O,BC是⊙O的直径,MN与⊙O相切,切点为A,若∠MAB=30°,则∠B=
度.
证明题
1、如图,C是以AB为直径的⊙O上一点,过O作OE⊥AC于点E,过点A作⊙O的切线
交OE的延长线于点F,
连结CF并延长交BA的延长线于点P.
⑴
求证:PC是⊙O的切线.⑵
若AB=4,,求CF的长.
如图,已知中,,平分,以为圆心、长为半径作,与的另一个交点为.
⑴
求证:与相切;⑵
若,求的长.
类型之二 与切线的判定有关的计算或证明
如图,⊙O的直径为AB,点C在圆周上(异于A,B),AD⊥CD.
(1)若BC=3,AB=5,求AC的值;
(2)若AC是∠DAB的平分线,求证:直线CD是⊙O的切线.
如图,在Rt△ACB中,∠ACB=90°,以AC为直径作⊙O交AB于点D,E为BC的中点,连结DE并延长交AC的延长线点F.
(1)求证:DE是⊙O的切线;
(2)若CF=2,DF=4,求⊙O直径的长.
如图,AB是⊙O的直径,点C,D在⊙O上,∠A=2∠BCD,点E在AB的延长线上,∠AED=∠ABC.
(1)求证:DE与⊙O相切;
(2)若BF=2,DF=,求⊙O的半径.
4
